非线性方程二分法
非线性方程二分法
优点:算法直观、简单、总能保证收敛;局限:收敛速度慢、一般不单独用它求根,仅为了获取根的粗略近似
文章目录
- 非线性方程二分法
- @[toc]
- 1 二分法基本思想
- 2 二分法实现
文章目录
- 非线性方程二分法
- @[toc]
- 1 二分法基本思想
- 2 二分法实现
1 二分法基本思想
设 f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]上连续、严格单调、满足条件
f ( a ) f ( b ) < 0 f(a)f(b)<0 f(a)f(b)<0
则在区间 [ a , b ] [a,b] [a,b]内必有一根 x ∗ x^* x∗。通过反复对分有根区间,以极限思想求解出非线性方程的数值解。具体步骤如下:
- 取 [ a , b ] [a,b] [a,b]的中点 x 0 = ( a + b ) / 2 x_0=(a+b)/2 x0=(a+b)/2,计算 f ( x 0 ) f(x_0) f(x0),当
- f ( a ) f ( x 0 ) < 0 f(a)f(x_0)<0 f(a)f(x0)<0,则令 a 1 = a , b 1 = x 0 a_1=a,b_1=x_0 a1=a,b1=x0;
- f ( x 0 ) f ( b ) < 0 f(x_0)f(b)<0 f(x0)f(b)<0,则令 a 1 = x 0 , b 1 = b a_1=x_0,b_1=b a1=x0,b1=b;
通过重复上述步骤,得到一系列有根区间
[ a , b ] ⊃ [ a 1 , b 1 ] ⊃ [ a 2 , b 2 ] ⊃ ⋯ ⊃ … [a,b]\supset [a_1,b_1]\supset[a_2,b_2]\supset\dots \supset\dots [a,b]⊃[a1,b1]⊃[a2,b2]⊃⋯⊃…
由于后一个区间长度是前一个区间的一半,通过递归公式求解出区间长度的通项公式
b k − a k = b − a 2 k b_k-a_k=\frac{b-a}{2^k} bk−ak=2kb−a
当 k → ∞ k\to \infty k→∞时, ∣ ∣ b k − a k ∣ ∣ → 0 ||b_k-a_k||\to0 ∣∣bk−ak∣∣→0,此时序列 { a k } , { b k } , { x k } → x ∗ \{a_k\},\{b_k\},\{x^k\} \to x^* {ak},{bk},{xk}→x∗,其中
x ∗ = a k + b k 2 x^*=\frac{a_k+b_k}{2} x∗=2ak+bk
由于方程根和中点间的距离真包含于 [ a k , b k ] [a_k,b_k] [ak,bk],故收敛速度
0 ≤ ∣ x ∗ − x k ∣ ≤ ( b k − a k ) / 2 = ( b − a ) / 2 k + 1 0\le|x^*-x_k|\le(b_k-a_k)/2=(b-a)/2^{k+1} 0≤∣x∗−xk∣≤(bk−ak)/2=(b−a)/2k+1
当 k → ∞ k\to \infty k→∞时,利用夹逼定理
lim k → ∞ 0 ≤ lim k → ∞ ∣ x ∗ − x k ∣ ≤ lim k → ∞ ( b − a ) / 2 k + 1 = 0 \mathop {\lim }\limits_{k\to \infty}0 \le \mathop {\lim }\limits_{k\to \infty}|x^*-x_k|\le\mathop {\lim }\limits_{k\to \infty}(b-a)/2^{k+1}=0 k→∞lim0≤k→∞lim∣x∗−xk∣≤k→∞lim(b−a)/2k+1=0
故有 x k → x ∗ x^k\to x^* xk→x∗。给定终止条件 ε \varepsilon ε,当
( b − a ) / 2 k + 1 < ε (b-a)/2^{k+1}<\varepsilon (b−a)/2k+1<ε
时,可求出满足精度 ε \varepsilon ε的最少二分次数 k k k。
2 二分法实现
求解:
f ( x ) = 2 x + x − 2 f(x)=2^x+x-2 f(x)=2x+x−2
function[xstar,index,it] = bisect(fun,a,b,ep)
% 非线性方程二分法
% fun为目标函数
% a,b为初始区间
% ep为精确度,当(b-a)/2<ep循环结束,迭代失败输出两端点函数值
% index指标变量,index = 1,迭代成功,index = 0表明初始区间不是有根区间
% it迭代次数
if nargin < 4ep = 1e-5;
end
fa = feval(fun,a); %计算a处的函数值
fb = feval(fun,b); %计算b处的函数值
if fa*fb>0xstar = [fa,fb];index = 0;it = 0;return
end
k = 0;
while abs(b-a)/2 >= epx = (a+b)/2;fx = feval(fun,x);if fx*fa<0b = x;fb = fx;elsea = x;fa = fx;endk = k +1;
end
xstar = (a+b)/2;index = 1;it = k
%具体函数
function f = fun1(x)
%测试函数
f = 2^x+x-2; %任意可改
endformat long
[xstar,index,it] = bisect(@fun1,0,2,0.0000001)
xstar = 0.543000400066376
index = 1
it = 24
参考文献
曾繁慧. 数值分析[M]. 中国矿业大学出版社,2009
相关文章:

非线性方程二分法
非线性方程二分法 优点:算法直观、简单、总能保证收敛;局限:收敛速度慢、一般不单独用它求根,仅为了获取根的粗略近似 文章目录 非线性方程二分法[toc]1 二分法基本思想2 二分法实现 1 二分法基本思想 设 f ( x ) f(x) f(x)在 [ …...
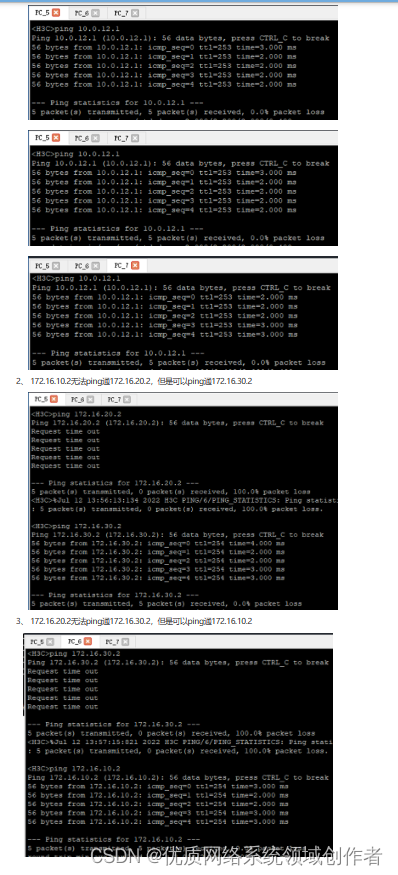
H3C防火墙单机旁路部署(网关在防火墙)
防火墙旁路部署在核心交换机上,内网有三个网段vlan 10:172.16.10.1/24、vlan 20:172.16.20.1/24、vlan30:172.16.30.1。要求内网网关在防火墙设备上,由防火墙作为DHCP服务器给终端下发地址,同时由防火墙来控…...
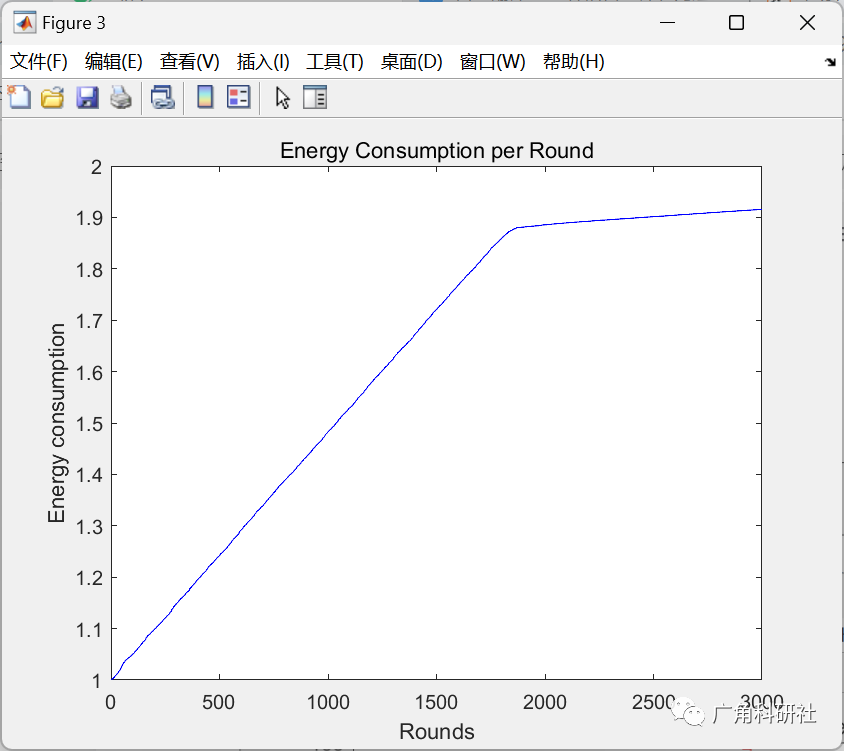
基于密度的无线传感器网络聚类算法的博弈分析(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨💻4 Matlab代码 💥1 概述 提高能源效率是无线传感器网络面临的关键挑战之一,无线传感器网络日益普遍。由于节点(传感器ÿ…...
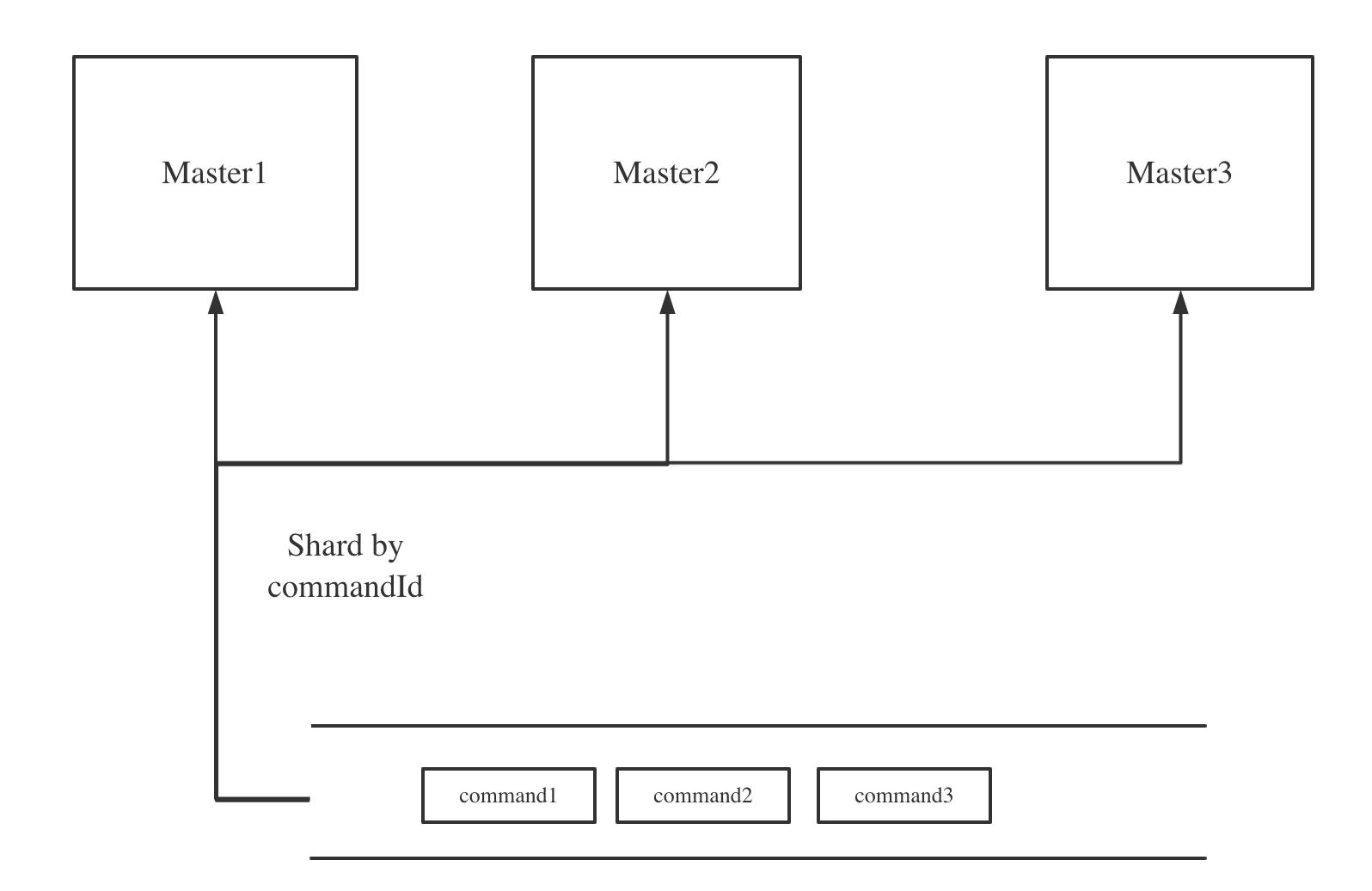
宕机了?!DolphinScheduler 高可用和 Failover 机制关键时刻保命
高可用性是 Apache DolphinScheduler 的特性之一。它通过冗余来避免单点问题,所有组件天然支持横向扩容;但仅仅保证了冗余还不够,当系统中有节点宕机时,还需要有故障转移机制能够自动将宕机节点正在处理的工作转移到新节点上执行&…...

try(){}用法try-with-resources、try-catch-finally
属于Java7的新特性。 经常会用try-catch来捕获有可能抛出异常的代码。如果其中还涉及到资源的使用的话,最后在finally块中显示的释放掉有可能被占用的资源。 但是如果资源类已经实现了AutoCloseable这个接口的话,可以在try()括号中可以写操作资源的语句(…...

常见Http错误码学习
常见 http 错误码 服务器巡检时比较常见的 http 错误码 400 Bad Request408 Request Timeout499 client has closed connection502 Bad Gateway504 Gateway Timeout 这些错误码反映了服务器什么样的状态,仅看字面意思还不太容易理解,就动手做个试验…...
)
qemu-基础篇——ARM 链接过程分析(六)
文章目录 ARM 链接过程分析源文件global_bss_file.cglobal_data_fle.cglobal_function_file.cglobal_rodata_file.cmain.c 链接文件 link.lds编译命令及反汇编命令解析 .o 文件global_bss_file.oglobal_data_fle.oglobal_function_file.oglobal_rodata_file.omain.o 链接观察链…...

Java企业工程项目管理系统+spring cloud 系统管理+java 系统设置+二次开发
工程项目各模块及其功能点清单 一、系统管理 1、数据字典:实现对数据字典标签的增删改查操作 2、编码管理:实现对系统编码的增删改查操作 3、用户管理:管理和查看用户角色 4、菜单管理:实现对系统菜单的增删改查操…...

Eureka与Zookeeper的区别
著名的CAP 理论指出,一个分布式系统不可能同时满足 C( 一致性 ) 、 A( 可用性 ) 和 P( 分区容错性 ) 。 由于分区容错性在是分布式系统中必须要保证的,因此我们只能在 A 和 C 之间进行权衡,在此 Zookeeper 保证的是 CP, 而 Eureka 则是 AP…...

顺序表和链表的各种代码实现
一、线性表 在日常生活中,线性表的例子比比皆是。例如,26个英文字母的字母表(A,B,C,……,Z)是一个线性表,表中的数据元素式单个字母。在稍复杂的线性表中,一个数据元素可以包含若干个数据项。例…...

C# 介绍三种不同组件创建PDF文档的方式
1 c# 数据保存为PDF(一) (spire pdf篇) 2 c# 数据保存为PDF(二) (Aspose pdf篇) 3 c# 数据保存为PDF(三) (PdfSharp篇) 组件名称 绘制…...

极简面试题 --- Redis
什么是 Redis? Redis 是一个基于内存的键值存储系统,也被称为数据结构服务器。它支持多种数据结构,例如字符串、哈希表、列表、集合和有序集合,并且可以在内存中快速读写。 Redis 的优势有哪些? 快速:由…...

可视化图表API格式要求有哪些?Sugar BI详细代码示例(4)
Sugar BI中的每个图表可以对应一个数据 API,用户浏览报表时,选定一定的过滤条件,点击「查询」按钮将会通过 API 拉取相应的数据;前面说过,为了确保用户数据的安全性,Sugar BI上的所有数据请求都在Sugar BI的…...
)
学习vue(可与知乎合并)
一:组件及交互 1、什么是组件? 组件是可复用的 Vue 实例,且带有一个名字:在这个例子中是 。我们可以在一个通过 new Vue 创建的 Vue 根实例中,把这个组件作为自定义元素来使用: 声明组件 // 定义一个名…...

【UEFI实战】Linux下如何解析ACPI表
本文介绍如何在Linux下查看ACPI表示。使用的系统是Ubuntu18.04: Linux home 4.15.0-36-generic #39-Ubuntu SMP Mon Sep 24 16:19:09 UTC 2018 x86_64 x86_64 x86_64 GNU/Linux 可以在如下的目录看到ACPI的基本信息: 但是默认的表都是不可以直接查看的&…...
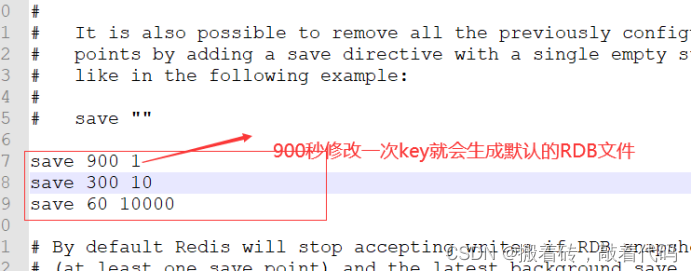
Java-Redis持久化之RDB操作
Java-Redis持久化之RDB操作 1.为什么redis需要持久化?2.什么是RDB操作?3.请你用自己的话讲下RDB的过程?4.如何恢复rdb文件? 1.为什么redis需要持久化? Redis是内存数据库,如果不将内存数据库保存到磁盘,那么服务器进程退出&am…...

信号signal编程测试
信号会打断系统调用,慎用,就是用的时候测一测。 下面是信号的基础测试 信号 信号(signal)机制是UNIX系统中最为古老的进程之间的通信机制。它用于在一个或多个进程之间传递异步信号。信号可以由各种异步事件产生,例如…...

Linux学习记录——이십삼 进程信号(2)
文章目录 1、可重入函数2、volatile关键字3、如何理解编译器的优化4、SIGCHLD信号 1、可重入函数 两个执行流都执行一个函数时,这个函数就被重入了。比如同一个函数insert,在main中执行时,这个进程时间片到了,嵌入了内核…...
Revit中如何创建曲面嵌板及一键成板
一、Revit中如何创建曲面嵌板 在我们的绘图过程中可能会遇见一些曲面形状,而我们的常规嵌板没办法满足我们绘制的要求,我们今天学习如何在revit中绘制曲面嵌板。 1.新建“自适应公制常规模型”族,创建4个点图元并为其使用自适应。 2.在相同的…...
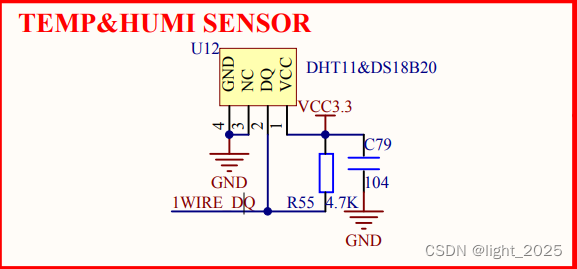
STM32F4_DHT11数字温湿度传感器
目录 前言 1. DHT11简介 2. DHT11数据结构 3. DHT11的传输时序 3.1 DHT11开始发送数据流程 3.2 主机复位信号和DHT11响应信号 3.3 数字 “0” 信号表示方法 3.4 数字 “1” 信号表示方法 4. 硬件分析 5. 实验程序详解 5.1 main.c 5.2 DHT11.c 5.3 DHT11.h 前言 DH…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
