JavaWeb ( 八 ) 过滤器与监听器
2.6.过滤器 Filter
Filter过滤器能够对匹配的请求到达目标之前或返回响应之后增加一些处理代码
常用来做 全局转码 ,session有效性判断

2.6.1.过滤器声明
在 web.xml 中声明Filter的匹配过滤特征及对应的类路径 , 3.0版本后可以在类上使用 @WebFilter 注解来声明
filter-class : 内部地址路径
url-pattern : 匹配过滤的特征, 实际开发中匹配规则的准确性非常重要
filter-name : 两者的对应
<filter><filter-name>myfilter</filter-name><filter-class>com.yuan.filter.MyFilter</filter-class></filter><filter-mapping><filter-name>myfilter</filter-name><url-pattern>*.do</url-pattern></filter-mapping>
2.6.2.过滤器生命周期

加载 : 在web.xml中声明Filter相关信息
实例化 : 由WebServer( 如 : Tomcat )根据web.xml中声明信息进行实例化, 实例化后才能调用方法
初始化 : 在init() 方法中,进行初始属性设置
过滤 : 用户发请求到达目标之前, 或者完成服务产生响应之后, 在 doFilter()方法中增加处理代码
销毁 : 当servlet被销毁时, 调用destroy()方法, 可以在这个方法中释放一些资源
垃圾回收 : 被JVM进行垃圾回收时, 调用 finalize() 方法
package com.yuan.filter;import javax.servlet.*;
import javax.servlet.annotation.WebFilter;
import java.io.IOException;@WebFilter
public class MyFilter implements Filter {@Overridepublic void init(FilterConfig filterConfig) throws ServletException {// 初始化方法}@Overridepublic void doFilter(ServletRequest servletRequest, ServletResponse servletResponse, FilterChain filterChain) throws IOException, ServletException {// 对请求进行加工filterChain.doFilter(servletRequest, servletResponse);}@Overridepublic void destroy() {// 销毁方法}
}
2.7.监听器Listener
Java Servlet的Listener是一种特殊的Java类,它可以监听Web应用程序中发生的事件,例如Servlet的生命周期事件、HTTP会话事件等。
它可以在Servlet容器启动时注册,当Web应用程序中发生事件时,容器会调用Listener的相应方法来处理它。
监听器Listener 用于监听web应用中某些对象、信息的创建、销毁、增加,修改,删除等动作的发生,然后作出相应的响应处理。
当范围对象的状态发生变化的时候,服务器自动调用监听器对象中的方法。
常见的Java Servlet Listener包括:
- ServletContextListener:用于监听Servlet上下文初始化和销毁事件。
- HttpSessionListener:用于监听HTTP会话的创建和销毁事件。
- ServletRequestListener:用于监听Servlet请求的创建和销毁事件。
- ServletRequestAttributeListener:用于监听Servlet请求属性的增删改事件。
- HttpSessionAttributeListener:用于监听HTTP会话属性的增删改事件。
通过监听这些事件,我们可以在应用程序初始化、销毁、或者在每个请求和会话之间共享信息、修改请求或响应、改变应用程序行为以及跟踪应用程序的状态等。
常用于 统计在线人数和在线用户,系统加载时进行信息初始化,统计网站的访问量等等。

2.7.1.Listener声明
在web.xml中声明
listener-class : 内部地址路径
<listener><listener-class>com.yuan.listener.MyListener</listener-class></listener>
2.7.2.实例
package com.yuan.listener;import javax.servlet.http.HttpSessionAttributeListener;
import javax.servlet.http.HttpSessionBindingEvent;public class MyListener implements HttpSessionAttributeListener {@Overridepublic void attributeAdded(HttpSessionBindingEvent se) {// 向session加入信息时执行的方法}@Overridepublic void attributeRemoved(HttpSessionBindingEvent se) {// 从session中移除信息时执行的方法}@Overridepublic void attributeReplaced(HttpSessionBindingEvent se) {// session中的信息被替换时执行的方法}
}
相关文章:

JavaWeb ( 八 ) 过滤器与监听器
2.6.过滤器 Filter Filter过滤器能够对匹配的请求到达目标之前或返回响应之后增加一些处理代码 常用来做 全局转码 ,session有效性判断 2.6.1.过滤器声明 在 web.xml 中声明Filter的匹配过滤特征及对应的类路径 , 3.0版本后可以在类上使用 WebFilter 注解来声明 filter-cla…...
Notion Ai中文指令使用技巧
Notion AI 是一种智能技术,可以自动处理大量数据,并从中提取有用的信息。它能够 智能搜索:通过搜索文本和查询结果进行快速访问 自动归档:可以根据关键字和日期自动将内容归档 内容分类:可以根据内容的标签和内容的…...
Linux一学就会——编写自己的shell
编写自己的shell 进程程序替换 替换原理 用fork创建子进程后执行的是和父进程相同的程序(但有可能执行不同的代码分支),子进程往往要调用一种exec函数 以执行另一个程序。当进程调用一种exec函数时,该进程的用户空间代码和数据完全被新程序替换,从新程序的启动 例程开始执行…...

编程练习【有效的括号】
给定一个只包括 (,),{,},[,] 的字符串 s ,判断字符串是否有效。 有效字符串需满足: 左括号必须用相同类型的右括号闭合。 左括号必须以正确的顺序闭合。 每个右括号都有一个对应的相同类型的左…...
)
Android 音频开发——桌面小部件(七)
对于收音机的车机 APP 开发,一般都有配套的桌面小部件(Widget)开发,这里对小部件的具体实现就不介绍了,这里主要介绍一些桌面(Launcher)中的小部件(Widget)弹出窗口功能实现。 一、功能描述 在小部件上点击按钮,弹出一个有音源选择列表的弹窗,点击其他位置…...

常见的C++包管理
C包管理工具 Conan 是一款免费开源的 C/C语言的依赖项和包管理器 类似于python的anaconda Introduction — conan 2.0.4 documentationconan-io/conan: Conan - The open-source C and C package manager (github.com) CPM cmake集成的 mirrors / cpm-cmake / CPM.cmake GitC…...

基于yolov7开发构建学生课堂行为检测识别系统
yolov7也是一款非常出众的目标检测模型,在我之前的文章中也有非常详细的教程系列的文章,感兴趣的话可以自行移步阅读即可。 《基于YOLOV7的桥梁基建裂缝检测》 《YOLOv7基于自己的数据集从零构建模型完整训练、推理计算超详细教程》 《基于YOLOv7融合…...

GPT-4 开始内测32k输入长度的版本了!你收到邀请了吗?
要说现在 GPT-4 最大的问题是什么?可能除了一时拿他没有办法的机器幻觉,就是卡死的输入长度了吧。尽管在一般的对话、搜索的场景里目前普通版本 GPT-4 的 8000 左右的上下文长度或许绰绰有余,但是在诸如内容生成、智能阅读等方面当下基础版的…...

如何用ChatGPT做新品上市推广方案策划?
该场景对应的关键词库(28个): 品牌、产品信息、新品、成分、属性、功效、人群特征、客户分析、产品定位、核心卖点、推广策略、广告、公关、线上推广、线下活动、合作伙伴、资源整合、预算、执行计划、监测、评估、微调方案、价值主张、营销策略、热点话…...

Qt之QGraphicsEffect的简单使用(含源码+注释)
文章目录 一、效果示例图1.效果演示图片3.弹窗演示图片 二.问题描述三、源码CFrame.hCFrame.cppCMainWindow.hCMainWindow.cpp 总结 一、效果示例图 1.效果演示图片 3.弹窗演示图片 二.问题描述 (因为全是简单使用,毫无技巧,直接描述问题&a…...

前端优化-css
1.css盒子模型 标准盒子模型,IE盒子模型 标准盒子模型:margin-border-padding-content IE盒子模型:margin-content(border-padding-content) 如何转换: box - sizing: border - box; // IE盒子模型 box - sizing: content - …...

第三方ipad笔哪个牌子好用?ipad触控笔推荐平价
至于选择苹果原装的电容笔,还是平替的电容笔,要看个人的需求而定,比如画图用的,可以用Apple Pencil;比如学习记笔记用的,可以用平替电容笔,目前的平替电容笔无论是品质还是性能,都非…...

windows10+detectron2完美安装教程
文章目录 前言下载detectron2安装Visual Studio 2019修改代码 前言 需要下载detectron2的github项目,安装vs2019 (强烈建议这个版本,其他的版本需要做更多地操作才能成功安装),默认其他环境没问题。 下载detectron2 链接:https…...

串口与wifi模块
经过以下学习,我们掌握: AT指令与wifi模块的测试方法:通过CH340直接测试,研究各种AT指令下wifi模块的响应信息形式。编程,使用串口中断接收wifi模块对AT指令的响应信息以及透传数据,通过判断提高指令执行的…...

上财黄烨:金融科技人才的吸引与培养
“金融科技企业在吸引人才前,应先完善人才培养机制,建立员工画像,有针对性地培训提高成员综合素质。” ——上海金融智能工程技术研究中心上海财经大学金融科技研究院秘书长&院长助理黄烨老师 01.何为数字人才? 目前大多数研…...
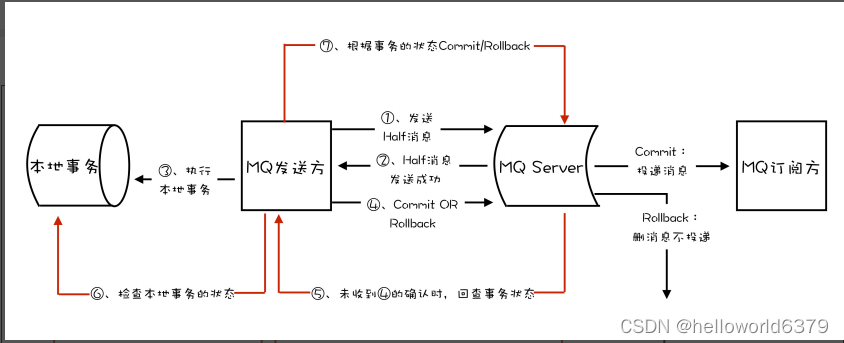
利用MQ事务消息实现分布式事务
MQ事务消息使用场景 消息队列中的“事务”,主要解决的是消息生产者和消息消费者的数据一致性问题。 拿我们熟悉的电商来举个例子。一般来说,用户在电商 APP 上购物时,先把商品加到购物车里,然后几件商品一起下单,最后…...

C++面向对象设计:深入理解多态与抽象类实现技巧
面向对象的多态 一、概念二、实现1. 静态多态1.1 函数重载1.2 运算符重载 2. 动态多态2.1 虚函数2.2 纯虚函数 三、虚函数1. 定义2. 实现3. 注意 四、纯虚函数1. 定义2. 作用 五、虚析构函数1. 定义2. 作用 六、 抽象类七、实现多态的注意事项1. 基类虚函数必须使用 virtual 关…...

长三角生物医药产业加速跑,飞桨螺旋桨为创新药企、医药技术伙伴装上AI大模型引擎...
生物医药是国家“十四五”规划中明确的战略性新兴产业之一。长三角地区是中国生物医药产业的排头兵,也是《“十四五”生物经济发展规划》的“生物经济先导区”之一。据《上海市生物医药产业投资指南》显示,2022 年上海市生物医药产业在 I 类国产创新药数…...
orin Ubuntu 20.04 配置 Realsense-ROS
librealsense安装 sudo apt-get install libudev-dev pkg-config libgtk-3-dev sudo apt-get install libusb-1.0-0-dev pkg-config sudo apt-get install libglfw3-dev sudo apt-get install libssl-dev sudo apt-get install ros-noetic-ddynamic-reconfigure二进制安装libr…...

MyBatis基础知识点总结
MyBatis了解 MyBatis 是什么? MyBatis 是支持定制化 SQL、存储过程以及高级映射的优秀的持久层框架 MyBatis 避免了几乎所有的 JDBC 代码和手动设置参数以及获取结果集 MyBatis 可以使用简单的XML或注解用于配置和原始映射,将接口和Java的 POJO&#x…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

Redis上篇--知识点总结
Redis上篇–解析 本文大部分知识整理自网上,在正文结束后都会附上参考地址。如果想要深入或者详细学习可以通过文末链接跳转学习。 1. 基本介绍 Redis 是一个开源的、高性能的 内存键值数据库,Redis 的键值对中的 key 就是字符串对象,而 val…...

RLHF vs RLVR:对齐学习中的两种强化方式详解
在语言模型对齐(alignment)中,强化学习(RL)是一种重要的策略。而其中两种典型形式——RLHF(Reinforcement Learning with Human Feedback) 与 RLVR(Reinforcement Learning with Ver…...

Go爬虫开发学习记录
Go爬虫开发学习记录 基础篇:使用net/http库 Go的标准库net/http提供了完善的HTTP客户端功能,是构建爬虫的基石: package mainimport ("fmt""io""net/http" )func fetchPage(url string) string {// 创建自定…...
shellcode混淆uuid/ipv6/mac)
【免杀】C2免杀技术(十五)shellcode混淆uuid/ipv6/mac
针对 shellcode 混淆(Shellcode Obfuscation) 的实战手段还有很多,如下表所示: 类型举例目的编码 / 加密XOR、AES、RC4、Base64、Poly1305、UUID、IP/MAC改变字节特征,避开静态签名或 YARA结构伪装PE Stub、GIF/PNG 嵌入、RTF OLE、UUID、IP/MAC看起来像合法文件/数据,弱…...

Git 切换到旧提交,同时保证当前修改不丢失
在 Git 中,可以通过以下几种方式切换到之前的提交,同时保留当前的修改 1. 使用 git checkout 创建临时分离头指针(推荐用于查看代码) git checkout <commit-hash>这会让你进入"分离头指针"状态,你可…...

C++信息学竞赛中常用函数的一般用法
在C 信息学竞赛中,有许多常用函数能大幅提升编程效率。下面为你介绍一些常见函数及其一般用法: 一、比较函数 1、max()//求出a,b的较大值 int a10,b5,c;cmax(a,b);//得出的结果就是c等于10. 2、min()//求出a,b的较小值 int a1…...
