Leetcode 322. 零钱兑换(完全背包)
- Leetcode 322. 零钱兑换(完全背包)
- 题目
- 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
- 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
- 你可以认为每种硬币的数量是无限的。
- 1 <= coins.length <= 12
- 1 <= coins[i] <= 2^31 - 1
- 0 <= amount <= 10^4
- 解法
- 动态规划之完全背包:
- 定义一维数组 dp,其中 dp[i] 表示组成总金额 i 所需的最少硬币数
- 初始化 dp 数组,dp[0] 为 0,表示组成金额 0 需要 0 个硬币,dp[1…amount] 初始化为极大值,表示当前无法组成该总金额
- 遍历硬币数组 coins,对于每种面额的硬币,遍历总金额范围内可以添加该硬币的金额下标。即 dp[j] 不为极大值,说明可以组成 j + coins[i] 金额,此时转移方程为:dp[j + coins[i]] = Math.min(dp[j + coins[i]], dp[j] + 1)
- 遍历结束后,dp[amount] 如果仍为极大值,则无法组成,返回 -1;否则返回 dp[amount] 表示最少需要的硬币数
- PS:由于 amount 最多由 amount 个硬币组成,因此初始化极大值只要大于 amount 就可以
- 代码
/*** 动态规划之完全背包:* 定义一维数组 dp,其中 dp[i] 表示组成总金额 i 所需的最少硬币数* 初始化 dp 数组,dp[0] 为 0,表示组成金额 0 需要 0 个硬币,dp[1...amount] 初始化为极大值,表示当前无法组成该总金额* 遍历硬币数组 coins,对于每种面额的硬币,遍历总金额范围内可以添加该硬币的金额下标。即 dp[j] 不为极大值,说明可以组成 j + coins[i] 金额,此时转移方程为:dp[j + coins[i]] = Math.min(dp[j + coins[i]], dp[j] + 1)* 遍历结束后,dp[amount] 如果仍为极大值,则无法组成,返回 -1;否则返回 dp[amount] 表示最少需要的硬币数* PS:由于 amount 最多由 amount 个硬币组成,因此初始化极大值只要大于 amount 就可以*/private static int solution(int[] coins, int amount) {// 判空if (amount == 0) {return 0;}if (coins == null || coins.length <= 0) {return -1;}// 定义且初始化 dp 数组int[] dp = new int[amount + 1];Arrays.fill(dp, 1, dp.length, Integer.MAX_VALUE);// 循环添加每一种硬币int coinsLen = coins.length;int dpLen = dp.length;for (int i = 0; i < coinsLen; i++) {for (int j = 0; j < dpLen - coins[i]; j++) {if (dp[j] < Integer.MAX_VALUE) {dp[j + coins[i]] = Math.min(dp[j + coins[i]], dp[j] + 1);}}}return dp[amount] == Integer.MAX_VALUE ? -1 : dp[amount];}
相关文章:
)
Leetcode 322. 零钱兑换(完全背包)
Leetcode 322. 零钱兑换(完全背包)题目 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额&…...
怎么恢复回收站?分享4个宝藏方法!
案例:怎么恢复回收站 【请问大家怎么恢复误删的文件呀?如果回收站被清空了,又应该怎么恢复呢?】 电脑回收站是我们存储被删除文件的地方。但是有时候,我们会不小心把一些重要的文件或者照片误删了。这时候࿰…...

大模型混战,最先实现“智慧涌现”的会是谁?
作者 | 曾响铃 文 | 响铃说 几秒钟写出了一篇欢迎词; 小说人物乱入现实,快速创作不重样的故事; 鼠标一点,一封英文工作沟通邮件撰写完成; 准确解出数学应用题,还给出解题步骤; 甚至还能理…...
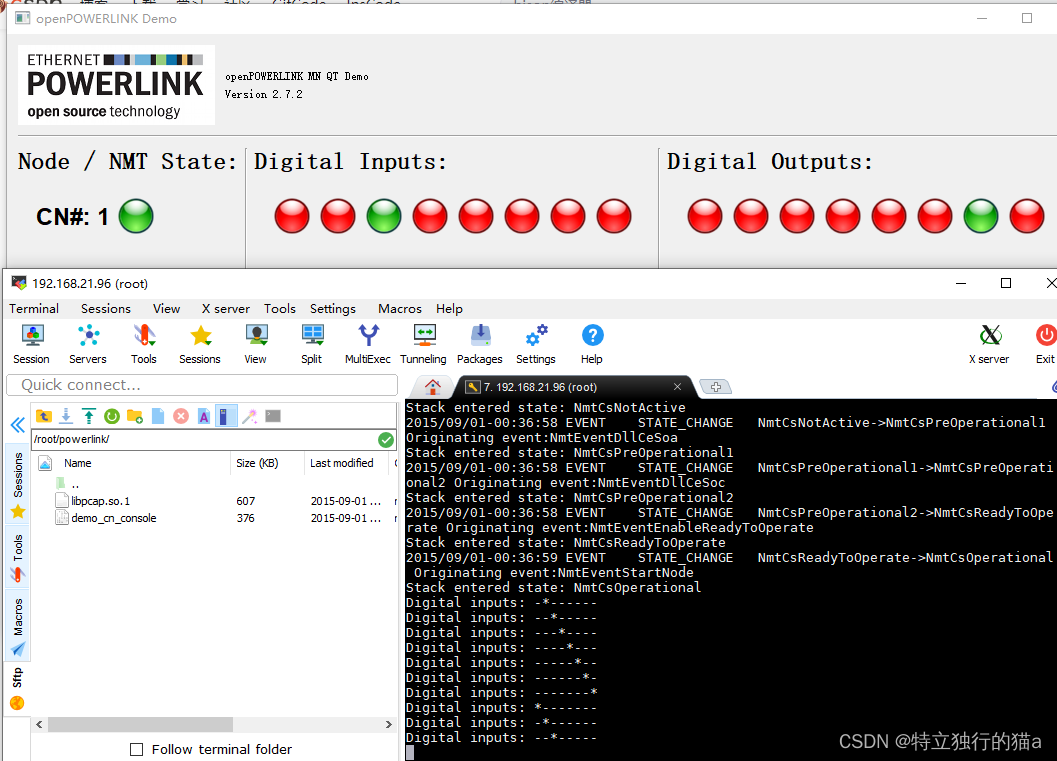
Powerlink协议在嵌入式linux上的移植和主从站通信(电脑和linux板通信实验)
使用最新的openPOWERLINK 2.7.2源码,业余时间搞定了Powerlink协议在嵌入式linux上的移植和测试,并进行了下电脑和linux开发板之间的通信实验。添加了一个节点配置,跑通了源码中提供的主站和从站的两个demo。这里总结下移植过程分享给有需要的…...
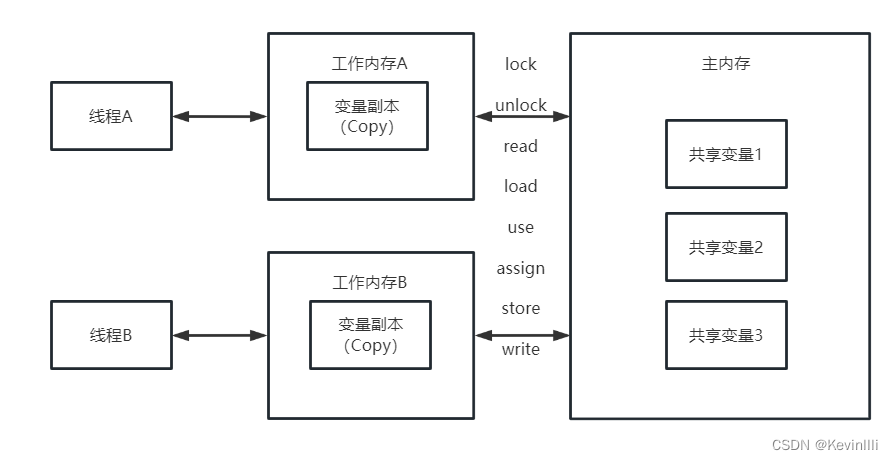
快速理解基本的cookie、session 和 redis
一、Cookie 1、什么是Cookie 1、Cookie实际上是一小段的文本信息,是一种keyvalue形式的字符串。客户端请求服务器,如果服务器需要记录该用户状态,就使用response向客户端浏览器颁发一个Cookie。客户端会把Cookie保存起来。 2、当浏览器再请求…...
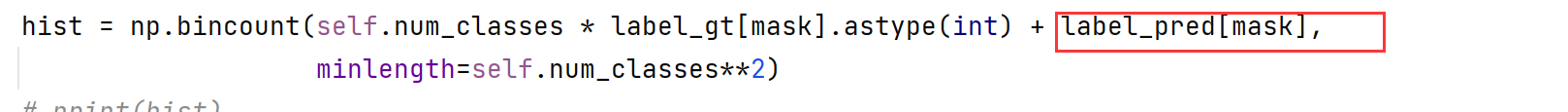
STANet代码复现出现的问题
1 IndexError: boolean index did not match indexed array along dimension 0; dimension is 4194304 but corresponding boolean dimension is 65536定位到导致错误的代码,是metric.py,Collect values for Confusion Matrix 收集混淆矩阵的值时出错 …...

Java 中String对象详解
Java语言中的String对象是一个非常常见的数据类型,大多数情况下我们都是在使用String对象来表示字符串类型的数据。Java中的String类是一个final class,它是不可被继承的。本文将对Java中的String对象进行详细全面的描述,包括以下几个方面&am…...
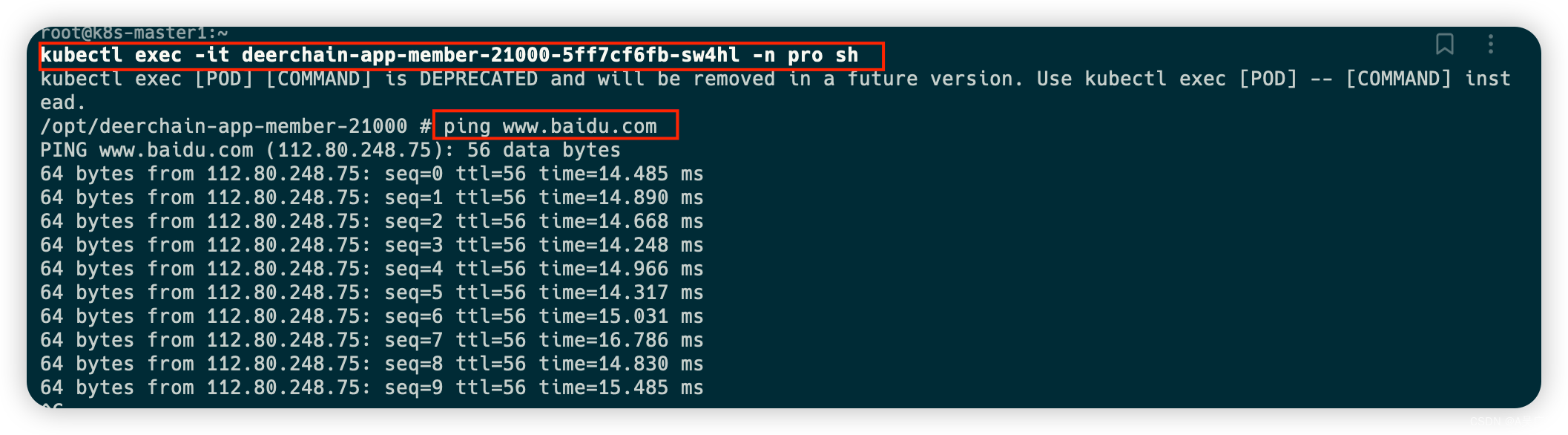
k8s nfs运行问题、etcd问题、calico网络问题
服务器重启后nfs运行问题导致服务不能正常重启 解决办法 在每个节点下使用如下命令进行查看nfs是否正常启动 systemctl status nfs 如果没有启动,则使用如下命令启动,保证三个节点下的nfs都正常启动 systemctl start nfs 再次查看nfs是否正常启动 syst…...

Qt--QString字符串类、QTimer定时器类
目录 1. QString 字符串类 dialog.cpp 2. 容器类 2.1 顺序容器 QList 示例代码: student.h student.cpp dialog.h dialog.cpp 运行结果: 2.2 关联容器 QMap 示例代码: dialog.h dialog.cpp 运行结果: 3. Qt类型 3.1 跨平台数据类型…...
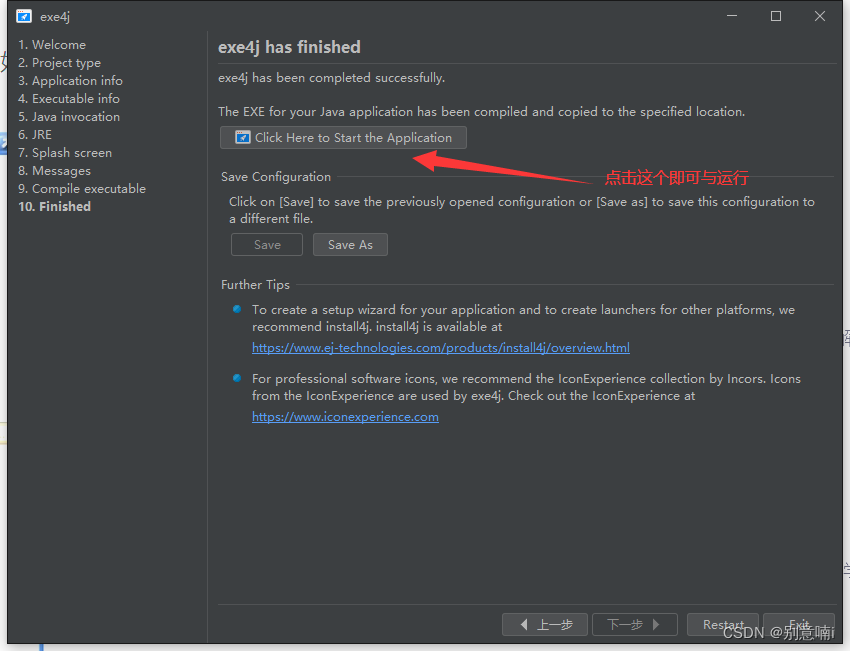
2023.5.13>>Eclipse+exe4j打包Java项目及获取exe所在文件的路径
Eclipseexe4j打包Java项目及获取exe所在文件的路径 1、打包exe文件1.1 打jar包1.2 打包exe2、在程序中获取exe所在路径3、遇到问题4、JDK version和class file version(Class编译版本号)对应关系5、参考文章 1、打包exe文件 1.1 打jar包 右单击项目选择“Export…” 1.2…...

Centos系统的使用基本教程
Centos是一款流行的Linux操作系统,它基于Red Hat Enterprise Linux系统,是一款稳定、可靠、安全的操作系统。本文将介绍Centos系统的基本使用方法,包括安装、命令行操作、软件安装和系统管理等方面的内容。 安装Centos系统 Centos系统可以从…...

IDEA生成ER图、UML类图、时序图、流程图等的插件推荐或独立工具推荐
以下是几个常用的IDEA插件和独立工具,可以用于生成ER图、UML类图、时序图、流程图等: Visual Paradigm (独立工具) Visual Paradigm是一个强大的建模工具,可以生成UML类图、时序图、流程图等。它支持多种语言和框架,包括Java、Spr…...

Python心经(3)
这一节总结点demo和常用知识点 目录 有关字符串格式化打印的 lambda匿名函数,,将匿名函数作为参数传入 文件读写 生成器 python的装饰器 简单的网站代码: 有关三元运算 推导式: 新浪面试题: 有关面向对象里…...

单工,半双工,全双工通讯
对于点对点之间的通信,按照消息传送的方向与时间关系,通信方式可分为单工通信、半双工通信及全双工通信三种。 单工通信 单工通信(Simplex Communication)是指消息只能单方向传输的工作方式。 在单工通信中,通信的信…...
)
【2023-05-09】 设计模式(单例,工厂)
2023-05-09 设计模式(单例,工厂) 单例模式 顾名思义,就是整个系统对外提供的实例有且只有一个 特点: 1、单例类只有一个实例 2、必须是自己创建唯一实例 3、必须给所以对象提供这个实例 分类ÿ…...
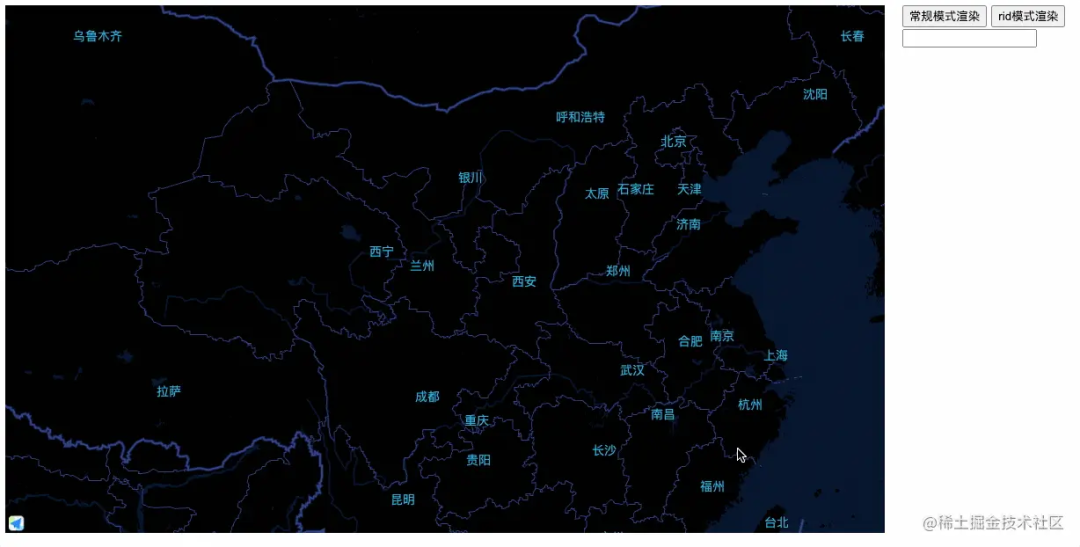
批量任务导致页面卡死解决方案
需求背景 需要基于高德地图展示海量点位(大概几万个),点位样式要自定义(创建DOM),虽然使用了聚合点,但初始化时仍需要将几万个点位的DOM结构都创建出来。 这里补充一句,高德地图在2.…...

避免“文献综抄”,5种写作结构助你完成文献综述→
很多作者可能有过这样的体验:读了很多文献,但在写综述的时候总感觉不像是在写文献综述,更像在写文献总结 如果引用方面不注意,甚至会成为文献综抄。 那么,你可以参考下我们整理的以下资料哦~ 01 文献总结和文献综述的…...

Java异常和反射
JAVA 异常分类及处理 概念 } final Entry<K,V> getEntryUsingComparator(Object key) { K k (K) key; // 获取该 TreeMap 的 comparator Comparator<? super K> cpr comparator; if (cpr ! null) { // 从根节点开始 Entry<K,V> p …...

Accesss数据库的那点事
Accesss数据库的那点事 1.Access的简介 Access(全称为Microsoft Access)是一个关系型数据库管理系统(RDBMS)。它是由微软公司开发的数据库软件,用于创建、管理和操作数据库应用程序。 Access提供了一个可视化的开发环…...

网络基础学习:osi网络七层模型
osi网络七层模型 什么是OSI,什么是ISO?为什么ISO要提出OSI网络七层模型?OSI七层的划分以及具体内容第七层 应用层第六层 表示层第五层 会话层第四层 传输层第三层 网络层第二层 数据链路层第一层 物理层 每一层与设备的对应关系 什么是OSI,什…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...
