Splay
前言
Splay是一种维护平衡二叉树的算法。虽然它常数大,而且比较难打,但Splay十分方便,而且LCT需要用到。
约定
cnticnt_icnti:节点iii的个数
valival_ivali:节点iii的权值
sizisiz_isizi:节点iii的子树大小
chi,0/1ch_{i,0/1}chi,0/1:节点iii的左右儿子
faifa_ifai节点iii的父亲
rootrootroot当前的根节点
tottottot当前的节点数量
gt(x)gt(x)gt(x):返回xxx是左儿子还是右儿子
pushup(x)pushup(x)pushup(x):更新当前子树大小
int gt(int x){return ch[fa[x]][1]==x;
}
void pt(int x){siz[x]=cnt[x]+siz[ch[x][0]]+siz[ch[x][1]];
}
基本操作
旋转操作

- yyy是zzz的哪个儿子,xxx就是zzz的哪个儿子
- xxx是yyy的哪个儿子,yyy就是xxx的对应儿子的兄弟
- xxx是yyy的哪个儿子,yyy的那个儿子就是xxx的对应儿子的兄弟
void rot(int x){int y=fa[x],z=fa[y],k=gt(x);ch[z][gt(y)]=x,fa[x]=z;ch[y][k]=ch[x][!k],fa[ch[y][k]]=y;ch[x][!k]=y,fa[y]=x;pt(y);pt(x);
}
伸展操作
splay(x,g)splay(x,g)splay(x,g),表示将xxx旋转到ggg下面。
我们可以一直rotrotrot,但如果xxx的父亲不是ggg且xxx和xxx的父亲是同一边的儿子,则可以旋转父亲。先旋转父亲可以减少深度。
void splay(int x,int g=0){for(int y;fa[x]!=g;rot(x)){y=fa[x];if(fa[y]!=g) rot((gt(x)==gt(y))?y:x);}if(!g) root=x;
}
普通操作
find操作
找到值最接近xxx的点,并伸展到根。
void find(int x){if(!root) return;int u=root;while(ch[u][x>v[u]]&&x^v[u]) u=ch[u][x>v[u]];splay(u);
}
insert操作
插入值为xxx的点,需进行一下操作
- 找到插入点的位置
- 如果存在值为xxx的点,则加对应的cntcntcnt
- 否则新加一个点
- 把该节点伸展到根
void insert(int x){int u=root,fu=0;while(u&&v[u]!=x){fu=u,u=ch[u][x>v[u]];}if(u) ++cnt[u];else{u=++tot;if(fu) ch[fu][x>v[fu]]=u;fa[u]=fu;v[u]=x;cnt[u]=siz[u]=1;}splay(u);
}
前驱和后继
求xxx的前驱和后继
先find(x)find(x)find(x),那么前驱就是左子树中最大的一个,后继就是右子树中最小的一个。
int nxt(int x,int f){find(x);int u=root;if(v[u]>x&&f) return u;if(v[u]<x&&!f) return u;u=ch[u][f];while(ch[u][!f]) u=ch[u][!f];return u;
}
delete操作
删除值为xxx的点
首先找到xxx的前驱sucsucsuc和xxx的后继preprepre,然后
- splay(pre)splay(pre)splay(pre)
- splay(suc,pre)splay(suc,pre)splay(suc,pre)
然后sucsucsuc的左子树就是要删除的点,删除即可。
void dele(int x){int lt=nxt(x,0),nt=nxt(x,1);splay(lt);splay(nt,lt);int tx=ch[nt][0];if(cnt[tx]>1) --cnt[tx],splay(tx);else ch[nt][0]=0;
}
kth操作
找到排名为kkk的节点的权值
int kth(int k){int u=root,sn=0;for(;;){sn=ch[u][0];if(k>siz[sn]+cnt[u]) k-=siz[sn]+cnt[u],u=ch[u][1];else if(siz[sn]>=k) u=sn;else return v[u];}
}
例题
普通平衡树
对于操作1,2,4,5,6,可以用上述操作解决即可。对于操作3,可以find(x)find(x)find(x)将其置为根,然后xxx的排名就是它左子树的节点个数+1+1+1。
注意为了防止splaysplaysplay出锅,要在加上两个节点∞\infty∞和−∞-\infty−∞。注意这两个节点对操作的影响。
#include<iostream>
#include<cstdio>
#define N 500000
using namespace std;
int root,tot,t,cnt[N],v[N],siz[N],ch[N][2],fa[N];
int gt(int x){return ch[fa[x]][1]==x;
}//Return 0 or 1 means x is the left or right son
void pt(int x){siz[x]=cnt[x]+siz[ch[x][0]]+siz[ch[x][1]];
}//Update the x
void rot(int x){int y=fa[x],z=fa[y],k=gt(x);ch[z][gt(y)]=x,fa[x]=z;ch[y][k]=ch[x][!k],fa[ch[y][k]]=y;ch[x][!k]=y,fa[y]=x;pt(y);pt(x);
}//Rotate
void splay(int x,int g=0){for(int y;fa[x]!=g;rot(x)){y=fa[x];if(fa[y]!=g) rot((gt(x)==gt(y))?y:x);}if(!g) root=x;
}//Put the x under the g
void find(int x){if(!root) return;int u=root;while(ch[u][x>v[u]]&&x^v[u]) u=ch[u][x>v[u]];splay(u);
}//Find the closest node and put it under the root
void insert(int x){int u=root,fu=0;while(u&&v[u]!=x){fu=u,u=ch[u][x>v[u]];}if(u) ++cnt[u];else{u=++tot;if(fu) ch[fu][x>v[fu]]=u;fa[u]=fu;v[u]=x;cnt[u]=siz[u]=1;}splay(u);
}//Insert the x
//1.Find the root which should be inserted
//2.If there is a node as same as it,plus its cnt
//3.Else plus a node
//4.Make the new node be the root
int nxt(int x,int f){find(x);int u=root;if(v[u]>x&&f) return u;if(v[u]<x&&!f) return u;u=ch[u][f];while(ch[u][!f]) u=ch[u][!f];return u;
}//Find the suc or the pre of the x
//After finding x,then
//The pre is the biggest one in left tree
//The suc is the smallest one in right tree
void dele(int x){int lt=nxt(x,0),nt=nxt(x,1);splay(lt);splay(nt,lt);int tx=ch[nt][0];if(cnt[tx]>1) --cnt[tx],splay(tx);else ch[nt][0]=0;
}//Find the pre and the suc of the x
//Splay(pre),splay(suc,pre)
//Then delete the left son of the suc
int kth(int k){int u=root,sn=0;for(;;){sn=ch[u][0];if(k>siz[sn]+cnt[u]) k-=siz[sn]+cnt[u],u=ch[u][1];else if(siz[sn]>=k) u=sn;else return v[u];}
}
int main()
{insert(2147483647);insert(-2147483647);scanf("%d",&t);while(t--){int op,x;scanf("%d%d",&op,&x);if(op==1) insert(x);else if(op==2) dele(x);else if(op==3) find(x),printf("%d\n",siz[ch[root][0]]);else if(op==4) printf("%d\n",kth(x+1));else if(op==5) printf("%d\n",v[nxt(x,0)]);else printf("%d\n",v[nxt(x,1)]);}return 0;
}
相关文章:

Splay
前言 Splay是一种维护平衡二叉树的算法。虽然它常数大,而且比较难打,但Splay十分方便,而且LCT需要用到。 约定 cnticnt_icnti:节点iii的个数 valival_ivali:节点iii的权值 sizisiz_isizi:节点iii的子…...
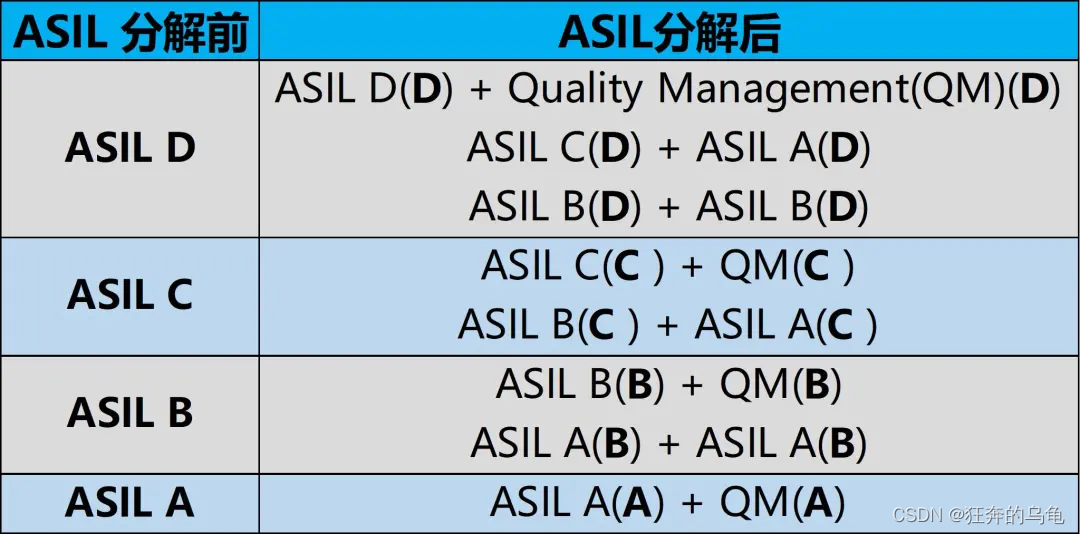
智能网联汽车ASIL安全等级如何划分
目录一、功能安全标准二、功能安全等级定义三、危险事件的确定四、ASIL安全等级五、危险分析和风险评定六、功能安全目标的分解一、功能安全标准 ISO 26262《道路车辆功能安全》脱胎于IEC 61508《电气/电子/可编程电子安全系统的功能安全》,主要定位在汽车行业&…...

Stable Diffusion 1 - 初始跑通 文字生成图片
文章目录关于 Stable DiffusionLexica代码实现安装依赖库登陆 huggingface查看 huggingface token下载模型计算生成设置宽高测试迭代次数生成多列图片关于 Stable Diffusion A latent text-to-image diffusion model Stable Diffusion 是一个文本到图像的潜在扩散模型ÿ…...
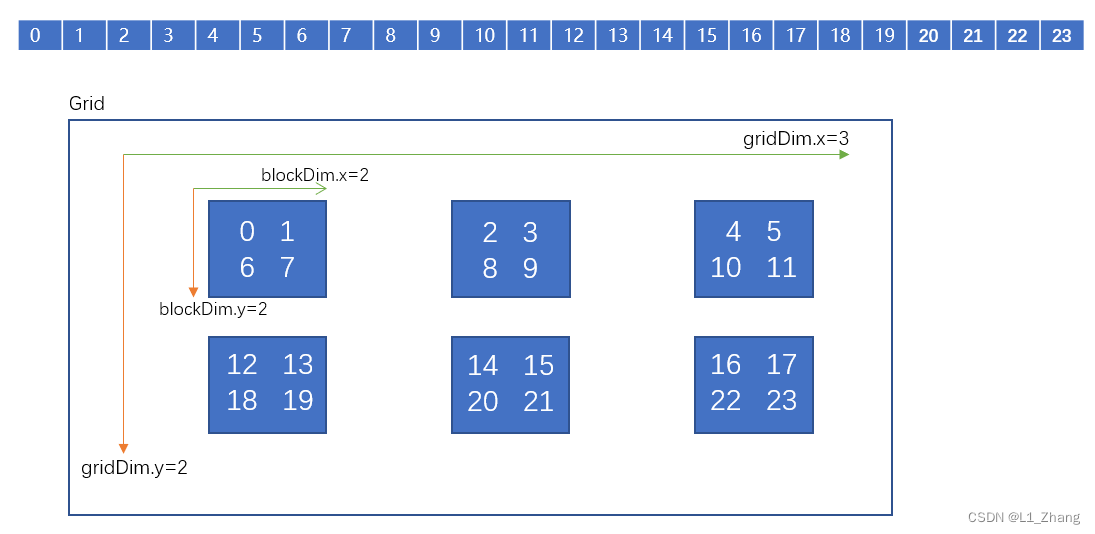
【cuda入门系列】通过代码真实打印线程ID
【cuda入门系列】通过代码真实打印线程ID1.gridDim(6,1),blockDim(4,1)2.gridDim(3,2),blockDim(2,2)【cuda入门系列之参加CUDA线上训练营】在Jetson nano本地跑 hello cuda! 【cuda入门系列之参加CUDA线上训练营】一文认识cuda基本概念 【cuda入门系列之参加CUDA线…...

【Python语言基础】——Python NumPy 数据类型
Python语言基础——Python NumPy 数据类型 文章目录 Python语言基础——Python NumPy 数据类型一、Python NumPy 数据类型一、Python NumPy 数据类型 Python 中的数据类型 默认情况下,Python 拥有以下数据类型: strings - 用于表示文本数据,文本用引号引起来。例如 “ABCD”…...

数据工程师需要具备哪些技能?
成为数据工程师需要具备哪些技能?数据工程工作存在于各个行业,在银行业、医疗保健业、大型科技企业、初创企业和其他行业找到工作机会。许多职位描述要求数据工程师、拥有数学或工程学位,但如果有合适的经验学位往往没那么重要。 大数据开发…...
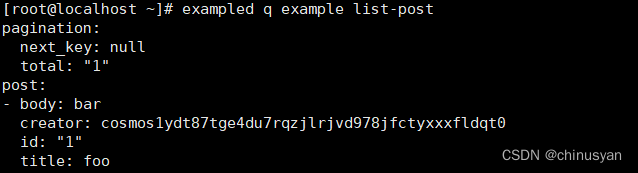
Cosmos 基础 -- Ignite CLI(二)Module basics: Blog
一、快速入门 Ignite CLI version: v0.26.1 在本教程中,我们将使用一个模块创建一个区块链,该模块允许我们从区块链中写入和读取数据。这个模块将实现创建和阅读博客文章的功能,类似于博客应用程序。最终用户将能够提交新的博客文章&#x…...

Quartz 快速入门案例,看这一篇就够了
前言 Quartz 是基于 Java 实现的任务调度框架,对任务的创建、修改、删除、触发以及监控这些操作直接提供了 api,这意味着开发人员拥有最大的操作权,也带来了更高的灵活性。 什么是任务调度? 任务调度指在将来某个特定的时间、固…...

图解LeetCode——1233. 删除子文件夹(难道:中等)
一、题目 你是一位系统管理员,手里有一份文件夹列表 folder,你的任务是要删除该列表中的所有 子文件夹,并以 任意顺序 返回剩下的文件夹。 如果文件夹 folder[i] 位于另一个文件夹 folder[j] 下,那么 folder[i] 就是 folder[j] …...
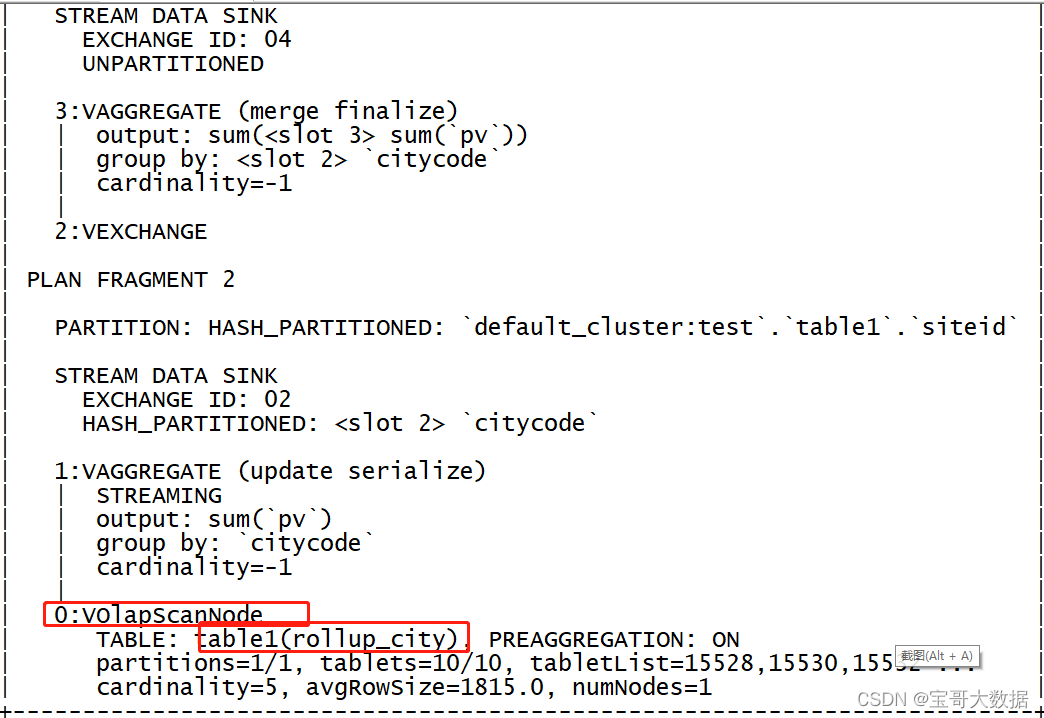
Doris--简单使用
一、数据表的创建与数据导入 1.1、创建表 1.1.1、单分区 CREATE TABLE table1 (siteid INT DEFAULT 10,citycode SMALLINT,username VARCHAR(32) DEFAULT ,pv BIGINT SUM DEFAULT 0 -- 聚合模型, value column 使用sum聚合 ) AGGREGATE KEY(siteid, citycode, …...

使用GPT让你的RStudio如虎添翼
API的的调用目前来说不限制地区,但是OpenAI的API的申请限制了地区。运行的时候,如果出现了429,意味着你被限流了,需要等一会才行。 前提是,你需要注册一个OpenAI的账户,然后在https://openai.com/api/ 里申…...

Python 算法交易实验45 再探量化
说明 去年大部分精力都在构建底层架构和工具了,一直都没有时间搞量化。目前底层的数据库服务(ADB)和清洗(衍生 AETL) 工具已经好了,我想尽快的把量化启动起来。 内容 1 思想 作为交易来说,只有买卖。通过数据分析与模型,我们获得的增强点是决策。在合适的时候进行买卖的…...

Dubbo加载配置文件方式,加载流程,加载配置文件源码解析
配置方法 API配置 以Java编码的方式组织配置,Dubbo3配置API详解 :https://dubbo.apache.org/zh/docs3-v2/java-sdk/reference-manual/config/api/#bootstrap-api public static void main(String[] args) throws IOException {ServiceConfig<Greet…...

十大开源测试工具和框架,一定有你需要的
目录 前言 Katalon Studio Selenium Appium JMeter SOAP UI Robot Framework Watir JUnit Robotium Citrus 总结 前言 免费的开源框架和工具由于其开源特性,现在逐渐成为自动化测试的首选解决方案。区别在于,你是喜欢使用类库编写一个全新的…...

加密技术在android中的应用
1、算法基础 算法基础参照linux的全盘加密与文件系统加密在android中的应用 消息摘要算法 对称加密算法 非对称加密算法...

备战蓝桥杯【一维前缀和】
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...

研报精选230214
目录 【行业230214艾瑞股份】中国增强现实(AR)行业研究报告【行业230214国信证券】信息安全深度剖析5:密评和信创双催化,密码产业开启从1到N【行业230214民生证券】磁性元器件深度报告:乘新能源之风,磁性元…...
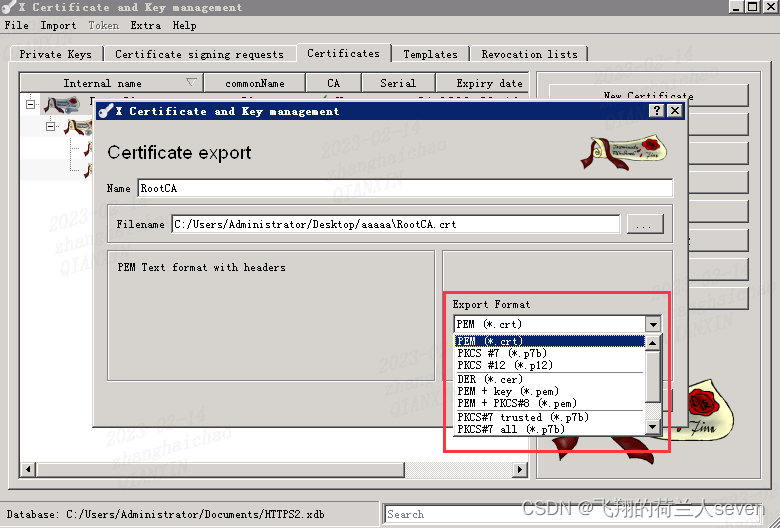
【SSL/TLS】准备工作:证书格式
证书格式1. 格式说明1.1 文件编码格式1.2 文件后缀格式2. xca导出格式1. 格式说明 1.1 文件编码格式 1. PEM格式: 使用Base 64 ASCII进行编码的纯文本格式。后缀为“.pem”, ".cer", ".crt", ".key" 2. DER格式 二进制编码格式,文件…...
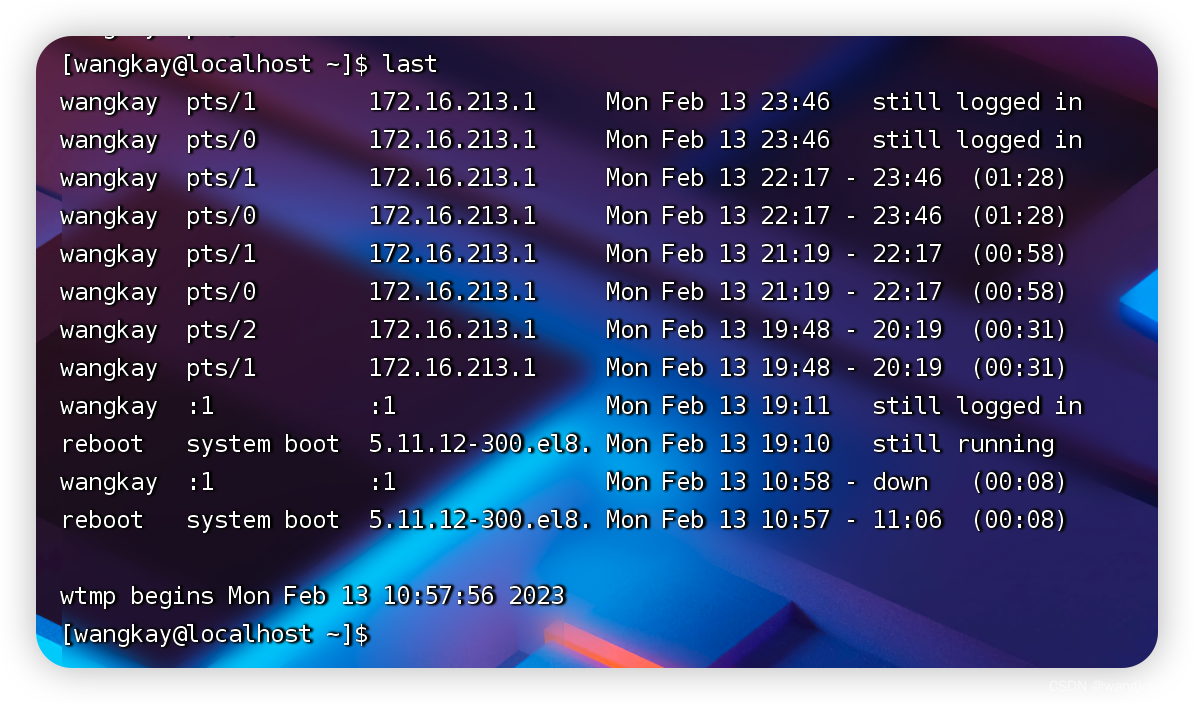
Linux常用命令---系统常用命令
Linux系统常用命令场景一: 查看当前系统内核版本相关信息场景二: sosreport 命令场景三: 如何定位并确定命令?场景四:查看当前系统运行负载怎场景五: 查看当前系统的内存可用情况场景六:查看网卡…...

C 结构体
C 数组允许定义可存储相同类型数据项的变量,结构是 C 编程中另一种用户自定义的可用的数据类型,它允许您存储不同类型的数据项。结构用于表示一条记录,假设您想要跟踪图书馆中书本的动态,您可能需要跟踪每本书的下列属性ÿ…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...
