【神经网络】tensorflow实验9--分类问题
1. 实验目的
①掌握逻辑回归的基本原理,实现分类器,完成多分类任务;
②掌握逻辑回归中的平方损失函数、交叉熵损失函数以及平均交叉熵损失函数。
2. 实验内容
①能够使用TensorFlow计算Sigmoid函数、准确率、交叉熵损失函数等,并在此基础上建立逻辑回归模型,完成分类任务;
②能够使用MatPlotlib绘制分类图。
- 实验过程
题目一:
观察6.5.3小节中给出的鸢尾花数据集可视化结果(如图1所示),编写代码实现下述功能:(15分)
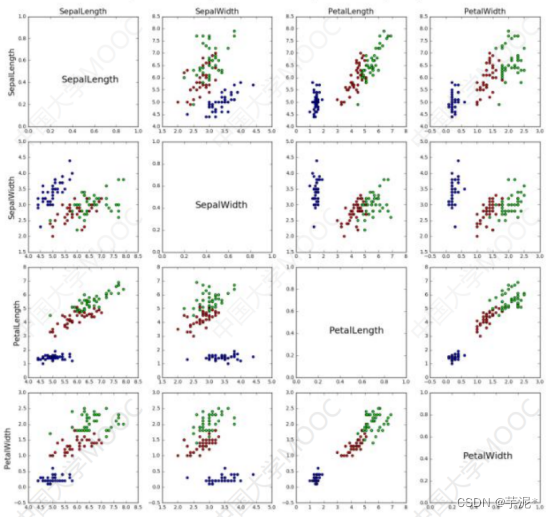
图1 鸢尾花数据集
要求:
⑴选择恰当的属性或属性组合,训练逻辑回归模型,区分山鸢尾和维吉尼亚鸢尾,并测试模型性能,以可视化的形式展现训练和测试的过程及结果。
⑵比较选择不同属性或属性组合时的学习率、迭代次数,以及在训练集和测试集上的交叉熵损失和准确率,以表格或合适的图表形式展示。
⑶分析和总结:
区分山鸢尾和维吉尼亚鸢尾,至少需要几种属性?说明选择某种属性或属性组合的依据;通过以上结果,可以得到什么结论,或对你有什么启发。
① 代码
import tensorflow as tf
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
TRAIN_URL='http://download.tensorflow.org/data/iris_training.csv'
train_path=tf.keras.utils.get_file(TRAIN_URL.split('/')[-1],TRAIN_URL)
df_iris=pd.read_csv(train_path,header=0)
iris=np.array(df_iris)#把二维数据表转化成二维numpy数组
train_x=iris[:,0:2]#取花萼的长度和宽度
train_y=iris[:,4]#取最后一列作为标签值
x_train=train_x[train_y!=1] #提取山鸢尾与维吉尼亚鸢尾
y_train=train_y[train_y!=1]#使用花萼长度和花萼宽度作为样本画散点图
num=len(x_train)
cm_pt=mpl.colors.ListedColormap(['b','r'])
plt.scatter(x_train[:,0],x_train[:,1],c=y_train,cmap=cm_pt) #色彩方案
# plt.show()
#使用花萼长度和花萼宽度作为样本画散点图 中心化后的图
x_train=x_train-np.mean(x_train,axis=0) #属性中心化 按列
plt.scatter(x_train[:,0],x_train[:,1],c=y_train,cmap=cm_pt)
# plt.show()#生成多元模型的属性矩阵和标签列向量X,Y
x0_train=np.ones(num).reshape(-1,1)
X=tf.cast(tf.concat((x0_train,x_train),axis=1),tf.float32)
Y=tf.cast(y_train.reshape(-1,1),tf.float32)#设置超参数
learn_rate=0.03
iter=50
display_step=10#设置模型变量初始值
np.random.seed(612)
W=tf.Variable(np.random.randn(3,1),dtype=tf.float32)#训练模型
ce=[]#保存每次交叉熵损失
acc=[]#保存准确率
for i in range(0,iter+1):with tf.GradientTape() as tape:PRED=1/(1+tf.exp(-tf.matmul(X,W)))Loss=-tf.reduce_mean(Y*tf.math.log(PRED)+(1-Y)*tf.math.log(1-PRED))accuracy=tf.reduce_mean(tf.cast(tf.equal(tf.where(PRED.numpy()<0.5,0.,1.),Y),tf.float32))ce.append(Loss)acc.append(accuracy)#加入数据dL_dW=tape.gradient(Loss,W)W.assign_sub(learn_rate*dL_dW)if i % display_step ==0:print('i:%i,Acc:%f,Loss:%f'%(i,accuracy,Loss))
#可视化
plt.figure(figsize=(5,3))
plt.plot(ce,color='b',label='Loss')
plt.plot(acc,color='r',label='acc')
plt.legend()
# plt.show()#绘制决策边界
plt.scatter(x_train[:,0],x_train[:,1],c=y_train,cmap=cm_pt)
x_=[-1.5,1.5]
y_=-(W[1]*x_+W[0]/W[2])
plt.plot(x_,y_,color='g')
# plt.show()np.random.seed(612)
W=tf.Variable(np.random.randn(3,1),dtype=tf.float32)
cm_pt=mpl.colors.ListedColormap(['b','r'])
x_=[-1.5,1.5]
y_=-(W[0]+W[1]*x_)/W[2]#绘制训练集的散点图
plt.scatter(x_train[:,0],x_train[:,1],c=y_train,cmap=cm_pt)
plt.plot(x_,y_,color='r',lw=3)
plt.xlim([-1.5,1.5])
plt.ylim([-1.5,1.5])#在训练过程中显示训练结果
ce=[]
acc=[]
for i in range(0,iter+1):with tf.GradientTape() as tape:PRED=1/(1+tf.exp(-tf.matmul(X,W)))Loss=-tf.reduce_mean(Y*tf.math.log(PRED)+(1-Y)*tf.math.log(1-PRED))accuracy=tf.reduce_mean(tf.cast(tf.equal(tf.where(PRED.numpy()<0.5,0.,1.),Y),tf.float32))ce.append(Loss)acc.append(accuracy)dL_dW=tape.gradient(Loss,W)W.assign_sub(learn_rate*dL_dW)if i % display_step ==0:print('i:%i,Acc:%f,Loss:%f'%(i,accuracy,Loss))y_=-(W[0]+W[1]*x_)/W[2]plt.plot(x_,y_)
plt.show()② 结果记录
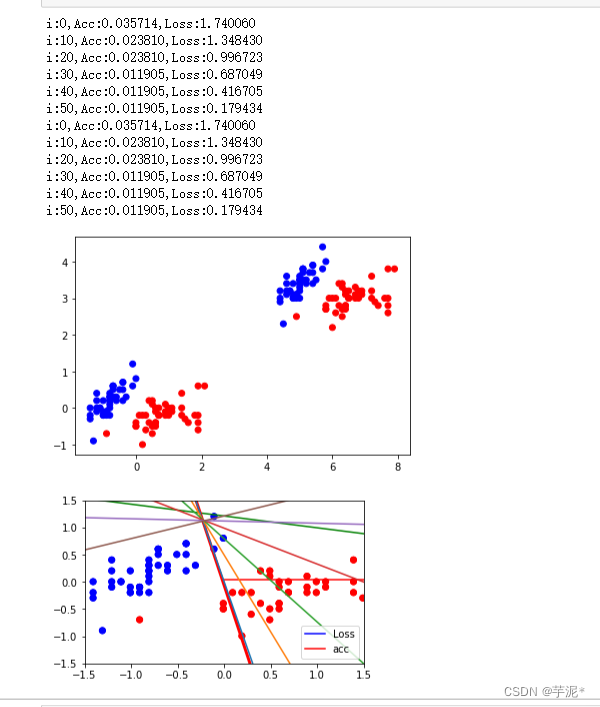
③ 实验总结
在训练集上训练的模型在测试集上也有比较好的效果,超参数需要不断调试才能达到一个比较好的效果.
题目二:
在Iris数据集中,分别选择2种、3种和4种属性,编写程序,区分三种鸢尾花。记录和分析实验结果,并给出总结。(20分)
⑴确定属性选择方案。
⑵编写代码建立、训练并测试模型。
⑶参考11.6小节例程,对分类结果进行可视化。
⑷分析结果:
比较选择不同属性组合时的学习率、迭代次数、以及在训练集和测试集上的交叉熵损失和准确率,以表格或合适的图表形式展示。
(3)总结:
通过以上分析和实验结果,对你有什么启发。
① 代码
import tensorflow as tf
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['Droid Sans Fallback']
# 下载鸢尾花数据集
TRAIN_URL = 'http://download.tensorflow.org/data/iris_training.csv'
TEST_URL = 'http://download.tensorflow.org/data/iris_test.csv'
# 获取文件名
train_path = tf.keras.utils.get_file(TRAIN_URL.split('/')[-1], TRAIN_URL)
test_path = tf.keras.utils.get_file(TEST_URL.split('/')[-1], TEST_URL)
COLUMN_NAMES = ['SepalLength', 'SepalWidth', 'PetalLength', 'PetalWidth', 'Species']df_iris_train = pd.read_csv(train_path, header=0)
iris_train = np.array(df_iris_train)# 提取长度,宽度
# x_train = iris_train[:, 2:4]
# y_train = iris_train[:, 4]#花萼宽度、花瓣长度、花瓣宽度
x_train = iris_train[:, 1:3]
y_train = iris_train[:, 4]
x_train=x_train[y_train>0]
y_train=y_train[y_train>0]
num_train = len(x_train)
#处理数据
x0_train = np.ones(num_train).reshape(-1, 1)
X_train = tf.cast(tf.concat([x0_train, x_train], axis=1), tf.float32)
Y_train = tf.one_hot(tf.constant(y_train, dtype=tf.int32), 3)#设置超参数 设置模型参数初始值
learn_rate = 0.2
iter = 500
display_step = 50
np.random.seed(612)
W = tf.Variable(np.random.randn(3,3), dtype=tf.float32)#训练模型
acc = []
cce = []
for i in range(0, iter + 1):with tf.GradientTape() as tape:PRED_train = tf.nn.softmax(tf.matmul(X_train, W))Loss_train = -tf.reduce_sum(Y_train * tf.math.log(PRED_train)) / num_trainaccuracy = tf.reduce_mean(tf.cast(tf.equal(tf.argmax(PRED_train.numpy(), axis=1), y_train), tf.float32))acc.append(accuracy)cce.append(Loss_train)dL_dW = tape.gradient(Loss_train, W)W.assign_sub(learn_rate * dL_dW)if i % display_step == 0:print('i:%i,Acc: %f,Loss: %f' % (i, accuracy, Loss_train))#绘制分类图
M = 500
x1_min, x2_min = x_train.min(axis=0)
x1_max, x2_max = x_train.max(axis=0)
t1 = np.linspace(x1_min, x1_max, M)
t2 = np.linspace(x2_min, x2_max, M)
m1, m2 = np.meshgrid(t1, t2)
m0 = np.ones(M * M)
X_ = tf.cast(np.stack((m0, m1.reshape(-1), m2.reshape(-1)), axis=1), tf.float32)
Y_ = tf.nn.softmax(tf.matmul(X_, W))
Y_ = tf.argmax(Y_.numpy(), axis=1) #转化为自然顺序码,决定网格颜色
n = tf.reshape(Y_, m1.shape)#绘制分类图
plt.figure(figsize=(8, 6))
cm_bg = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
plt.pcolormesh(m1, m2, n, cmap=cm_bg)
plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train, cmap='brg')
plt.show()② 结果记录
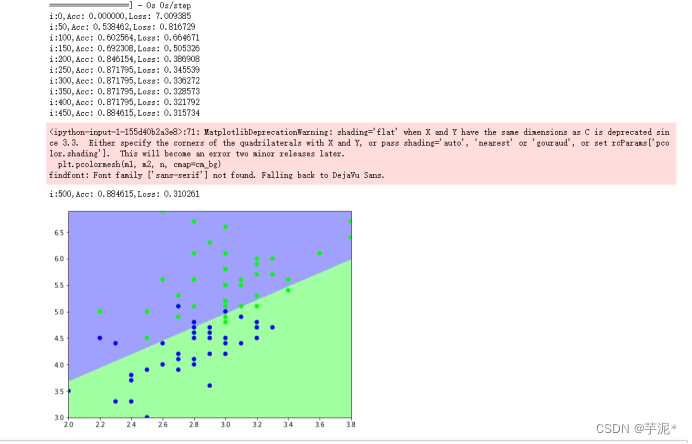
③ 实验总结
在训练集上训练的模型在测试集上也有比较好的效果,超参数需要不断调试才能达到一个比较好的效果.
| 学习率 | 训练轮数 | 测试损失值 | 测试集准确率 | 所花时间 | |
| 1 | 1e-3 | 1000 | 0.483739 | 87.2% | 1.73s |
| 2 | 1e-4 | 10000 | 0.483747 | 87.2% | 16.68s |
| 3 | 5e-2 | 1000 | 0.211227 | 93.6% | 1.73s |
拓展题(选做):
乳腺癌肿瘤数据集,由威斯康辛大学麦迪逊医院的William博士提供,可在UCI数据库(加州大学欧文分校提出的用于机器学习的数据库)里下载。
下载地址:https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data
该数据集中有699个乳腺癌肿瘤样本,每个样本包含10个属性和1个肿瘤标签,其结构如图1所示。第1列为id号,第2-10列为肿瘤特征,第11列为肿瘤的标签。每个属性的属性值均为0-9之间的整数,标签值取2或4,2表示良性、4表示恶性。
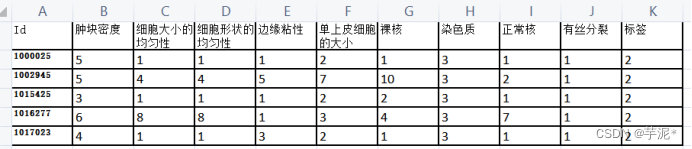
图1 乳腺癌肿瘤数据集(前5行数据)
要求:
⑴下载并划分数据集:
下载数据集,合理划分为训练集和测试集;
⑵数据预处理:
数据集中有16处缺失值,用“?”表示,在将数据输入模型之前,需要对这些缺失值进行处理。首先将“?”替换为NaN,再丢弃缺失值所在的样本,最后对已经丢弃缺失值的数组索引进行重置;
相关函数:
| 序号 | 函数 | 函数功能 | 函数相关库 |
| (1) | 对象名.replace(to_replace=’?’,value=np.nan) | 将问号替换为NaN | Python内置函数 |
| (2) | 对象名.dropna() | 丢弃缺失值 | Pandas库 |
| (3) | 对象名.reset_index() | 索引重置 | Pandas库 |
(3)建立逻辑回归模型,使用属性“肿块密度”和“细胞大小的均匀性”训练模型,综合考虑准确率、交叉熵损失、和训练时间等,使模型在测试集达到最优的性能,并以合适的形式展现训练过程和结果;
(4)选择其他属性或属性组合训练模型:
尝试选择数据集中的其他属性或者属性组合,训练和测试逻辑回归模型,并展现训练过程和结果;
(5)分析和总结:
比较采用不同的属性或属性组合训练模型时,学习率、迭代次数,以及交叉熵损失、准确率和模型训练时间等,以表格或其他合适的图表形式展示。通过以上结果,可以得到什么结论,或对你有什么启发。
① 代码
② 结果记录
③ 实验总结
3. 实验小结&讨论题
①实现分类问题的一般步骤是什么?实现二分类和多分类问题时有什么不同之处?哪些因素会对分类结果产生影响?
答:1.问题的提出2.神经网络模型的搭建和训3.结果展示。
多分类:
每个样本只能有一个标签,比如ImageNet图像分类任务,或者MNIST手写数字识别数据集,每张图片只能有一个固定的标签。
对单个样本,假设真实分布为,网络输出分布为,总的类别数为,则在这种情况下,交叉熵损失函数的计算方法如下所示,我们可以看出,实际上也就是计算了标签类别为1的交叉熵的值,使得对应的信息量越来越小,相应的概率也就越来越大了。
二分类:
对于二分类,既可以选择多分类的方式,也可以选择多标签分类的方式进行计算,结果差别也不会太大
②将数据集划分为训练集和测试集时,应该注意哪些问题?改变训练集和测试集所占比例,对分类结果会有什么影响?
答:同样的迭代次数,和学习率下,随着训练集的比例逐渐变大,训练集交叉熵损失大致变小准确率变高的趋势,测试集交叉熵损失大致变大准确率变高的趋势。
③当数据集中存在缺失值时,有哪些处理的方法?查阅资料并结合自己的思考,说明不同处理方法的特点和对分类结果的影响。
答:(1)删除,直接去除含有缺失值的记录,适用于数据量较大(记录较多)且缺失比较较小的情形,去掉后对总体影响不大。
(2)常量填充,变量的含义、获取方式、计算逻辑,以便知道该变量为什么会出现缺失值、缺失值代表什么含义。
(3)插值填充,采用某种插入模式进行填充,比如取缺失值前后值的均值进行填充。
(4)KNN填充
(5)随机森林填充,随机森林算法填充的思想和knn填充是类似的,即利用已有数据拟合模型,对缺失变量进行预测。
相关文章:

【神经网络】tensorflow实验9--分类问题
1. 实验目的 ①掌握逻辑回归的基本原理,实现分类器,完成多分类任务; ②掌握逻辑回归中的平方损失函数、交叉熵损失函数以及平均交叉熵损失函数。 2. 实验内容 ①能够使用TensorFlow计算Sigmoid函数、准确率、交叉熵损失函数等,…...
LeetCode2. 两数相加
写在前面: 题目链接:LeetCode2两数相加 编程语言:C 题目难度:中等 一、题目描述 给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。 …...

基于无线传感网络(WSN)的目标跟踪技术(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨💻4 Matlab代码 💥1 概述 无线传感器网络由于其自组织性、鲁棒性及节点数量巨大的特点,非常适合于目标跟踪。无线传感器网络中的移动目标跟踪实际上就是…...

百度发布首个可信AI工具集TrustAI,助力数据分析与增强
百度发布首个集分析与增强于一体的可信AI工具集TrustAI,该工具集旨在帮助用户快速、准确地对各种类型的数据进行分析和增强,从而提高数据的价值和可信度。 随着人工智能技术的快速发展,数据的价值和重要性日益凸显。然而,在数据处…...
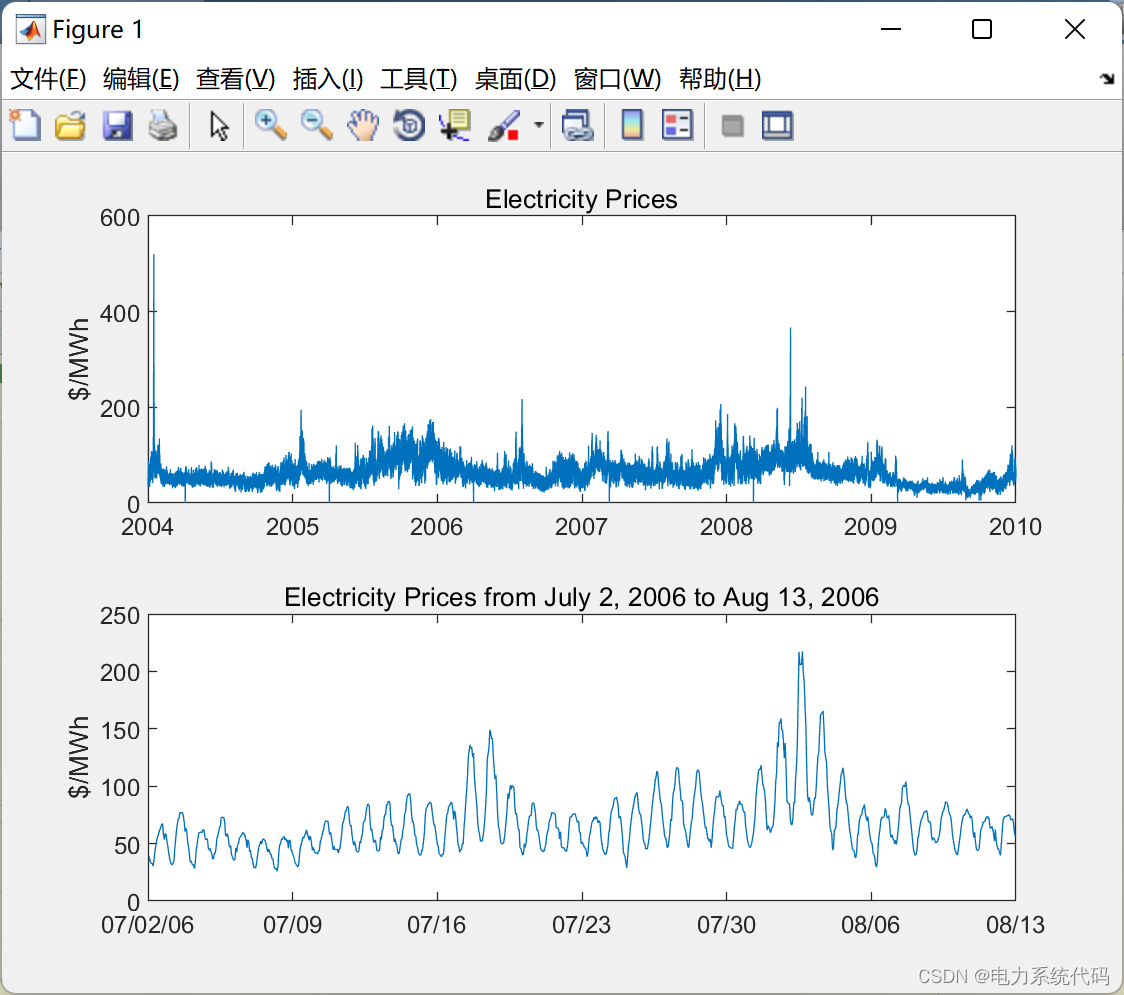
电力系统负荷与电价预测优化模型(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
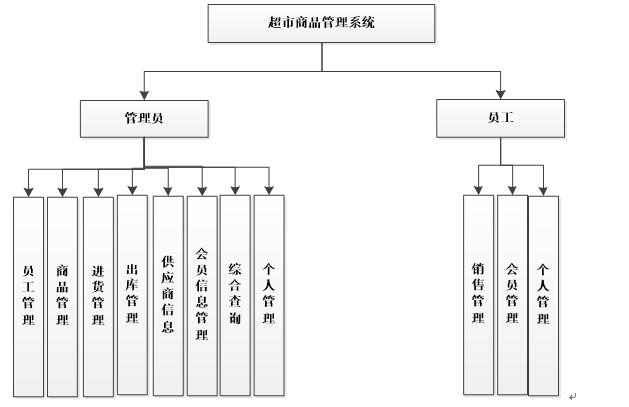
asp.net+C#超市商品进销存管理系统
本超市商品管理系统主要超市内部提供服务,系统分为管理员员工两部分。 本研究课题重点主要包括了下面几大模块:管用户登录,员工管理,商品管理,进货管理,销售管理,供应商信息,会员信…...

轻量级K8s发行版的五大优势,助力企业快速拥抱边缘计算
随着物联网和移动设备的普及,边缘计算已成为当前信息技术领域的热门话题。为了满足这一需求,越来越多的企业开始探索使用容器化技术来打造轻量级的K8s发行版。这种发行版可以更加灵活地部署在物理边缘,提供更快速、更稳定的服务。 在这篇文章…...
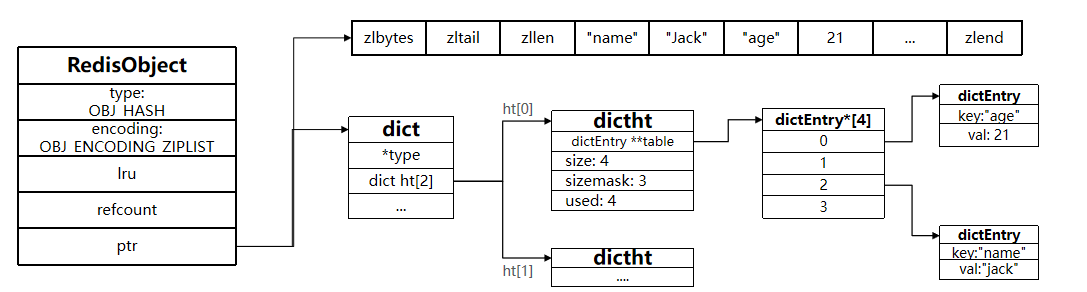
【深入理解redis】数据结构
文章目录 动态字符串SDS字符串编码类型 intsetDictZipListZipList的连锁更新问题 QuickListSkipListRedisObjectStringListSet结构ZSETHash Redis 共有 5 种基本数据结构:String(字符串)、List(列表)、Set(…...

《计算机网络—自顶向下方法》 第三章Wireshark实验:DNS协议分析
域名系统 DNS(Domain Name System) 是互联网使用的命名系统,用于把便于大家使用的机器名字转换为 IP 地址。许多应用层软件经常直接使用 DNS,但计算机的用户只是间接而不是直接使用域名系统。 互联网采用层次结构的命名树作为主机的名字,并使…...
-线程中断相关问题(LockSupport,sleep,InterruptException))
JUC(十二)-线程中断相关问题(LockSupport,sleep,InterruptException)
JUC线程中断相关问题总结 线程中断相关问题总结 JUC线程中断相关问题总结一、 sleep 和线程中断之间的关系和特点结论测试验证代码如下 二、 LockSupport 和线程中断之间的关系结论测试验证代码如下 一、 sleep 和线程中断之间的关系和特点 结论 线程调用 Thread.sleep之后会进…...

Kotlin高级协程
Kotlin高级协程 一.前言二.先从线程说起三.协程的设计思想四.协程特点:优雅的实现移步任务五.协程基本使用六.协程和线程相比有什么特点,如何优雅的实现异步任务 一.前言 在文章正式上干货之前,先说一点背景吧;我是 Kotlin 协程官…...

车载软件架构——闲聊几句AUTOSAR BSW(四)
我是穿拖鞋的汉子,魔都中坚持长期主义的工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 我们并不必要为了和谐,而时刻保持通情达理;我们需要具备的是,偶尔有肚量欣然承认在某些方面我们可能会有些不可理喻。该有主见的时候能掷地有声地镇得住场…...
Linux:rpm查询安装 yum安装
环境: 需要插入安装镜像 镜像内有所需的安装库 我这里使用的虚拟机直接连接光盘 连接的光盘挂载在/dev/cdrom 由于我们无法直接进入,所以选择把/dev/cdrom挂载到别的地方即可 mount /dev/cdrom /123 将/dev/cdrom 挂载到 /123 目录下 Packages下就是…...

Android音视频开发之音频录制和播放
1.封装音频录制工具类: public class RecorderAudioManagerUtils {private static volatile RecorderAudioManagerUtils mInstance;public static RecorderAudioManagerUtils getInstance() {if (mInstance null) {synchronized (RecorderAudioManagerUtils.class…...

Java之单例模式
目录 一.上节内容 1.什么是线程安全 2.线程不安全的原因 3.JMM(Java内存模型) 4.synchronized锁 5.锁对象 6.volatile关键字 7.wait()和notify() 8.Java中线程安全的类 二.单例模式 1.什么是单例 2.怎么设计一个单例 1.口头约定 2.使用编程语言的特性 三.饿汉模式…...

【分组码系列】线性分组码的网格图和维特比译码
线性分组码的网格图 由于码字的比特位是统计独立的,所以编码过程可以利用有限状态机来描述,它能精确地确定初始和最终状态。可以利用网格图进一步描述编码过程[36],采用维特比算法进行最大似然译码. 在GF(2)上定义线性分组码(n,k)。相应的(n-k)Xn维校验阵可以写成 令码字为系…...
代码命名规范是真优雅呀!代码如诗
日常编码中,代码的命名是个大的学问。能快速的看懂开源软件的代码结构和意图,也是一项必备的能力。那它们有什么规律呢? Java项目的代码结构,能够体现它的设计理念。Java采用长命名的方式来规范类的命名,能够自己表达…...
你不知道的自动化?使用自动化测试在项目中创造高业务价值...
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 脱离数据支撑谈价…...

通过实现一个简单的 JavaScript 猜数字大小的游戏,介绍如何进行布局样式处理
JavaScript 猜数字大小是一个非常简单、却又经典的游戏,可以锻炼玩家的逻辑思维能力。在这个游戏中,电脑会随机生成一个数字,玩家需要根据提示逐步猜出正确的数字。接下来,我们将通过实现一个简单的 JavaScript 猜数字大小游戏来介…...
策略模式)
Java设计模式(二十二)策略模式
一、概述 策略模式是一种行为型设计模式,它允许在运行时选择算法的行为。策略模式通过将算法封装成独立的策略类,使得它们可以相互替换,而不影响使用算法的客户端。这样可以使客户端代码与具体算法的实现细节解耦,提高了代码的可…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

FOPLP vs CoWoS
以下是 FOPLP(Fan-out panel-level packaging 扇出型面板级封装)与 CoWoS(Chip on Wafer on Substrate)两种先进封装技术的详细对比分析,涵盖技术原理、性能、成本、应用场景及市场趋势等维度: 一、技术原…...

【Java多线程从青铜到王者】单例设计模式(八)
wait和sleep的区别 我们的wait也是提供了一个还有超时时间的版本,sleep也是可以指定时间的,也就是说时间一到就会解除阻塞,继续执行 wait和sleep都能被提前唤醒(虽然时间还没有到也可以提前唤醒),wait能被notify提前唤醒…...

开源 vGPU 方案:HAMi,实现细粒度 GPU 切分
本文主要分享一个开源的 GPU 虚拟化方案:HAMi,包括如何安装、配置以及使用。 相比于上一篇分享的 TimeSlicing 方案,HAMi 除了 GPU 共享之外还可以实现 GPU core、memory 得限制,保证共享同一 GPU 的各个 Pod 都能拿到足够的资源。…...

Java严格模式withResolverStyle解析日期错误及解决方案
在Java中使用DateTimeFormatter并启用严格模式(ResolverStyle.STRICT)时,解析日期字符串"2025-06-01"报错的根本原因是:模式字符串中的年份格式yyyy被解释为YearOfEra(纪元年份),而非…...

鸿蒙APP测试实战:从HDC命令到专项测试
普通APP的测试与鸿蒙APP的测试有一些共同的特征,但是也有一些区别,其中共同特征是,它们都可以通过cmd的命令提示符工具来进行app的性能测试。 其中区别主要是,对于稳定性测试的命令的区别,性能指标获取方式的命令的区…...
