LeetCode周赛复盘(第345场周赛)
文章目录
- 1、找出转圈游戏输家
- 1.1 题目链接
- 1.2 题目描述
- 1.3 解题代码
- 1.4 解题思路
- 2、相邻值的按位异或
- 2.1 题目链接
- 2.2 题目描述
- 2.3 解题代码
- 2.4 解题思路
- 3、 矩阵中移动的最大次数
- 3.1 题目链接
- 3.2 题目描述
- 3.3 解题代码
- 3.4 解题思路
- 4、 统计完全连通分量的数量
- 4.1 题目链接
- 4.2 题目描述
- 4.3 解题代码
- 4.4 解题思路
- 打鸡血
1、找出转圈游戏输家
1.1 题目链接
点击跳转到题目位置
1.2 题目描述
n 个朋友在玩游戏。这些朋友坐成一个圈,按 顺时针方向 从 1 到 n 编号。从第 i 个朋友的位置开始顺时针移动 1 步会到达第 (i + 1) 个朋友的位置(1 <= i < n),而从第 n 个朋友的位置开始顺时针移动 1 步会回到第 1 个朋友的位置。
游戏规则如下:
第 1 个朋友接球。
接着,第 1 个朋友将球传给距离他顺时针方向 k 步的朋友。
然后,接球的朋友应该把球传给距离他顺时针方向 2 * k 步的朋友。
接着,接球的朋友应该把球传给距离他顺时针方向 3 * k 步的朋友,以此类推。
换句话说,在第 i 轮中持有球的那位朋友需要将球传递给距离他顺时针方向 i * k 步的朋友。
当某个朋友第 2 次接到球时,游戏结束。
在整场游戏中没有接到过球的朋友是 输家 。
给你参与游戏的朋友数量 n 和一个整数 k ,请按升序排列返回包含所有输家编号的数组 answer 作为答案。
1.3 解题代码
class Solution {unordered_map<int, int> hash;
public:vector<int> circularGameLosers(int n, int k) {int i = 0;int m = 1;while(hash[i] == 0){hash[i] = 1;i = (i + m * k) % n; ++m;}vector<int> res;for(int i = 0; i < n; ++i){if(hash[i] == 0){res.push_back(i+1);}}return res;}
};
1.4 解题思路
(1) 模拟题,首先我们要弄懂模拟规则,用一个参数m来表示传到第几次了。然后下标i从0开始(不是题目中从1开始),其目的就是为了方便进行模运算。
(2) 每次下标变换到的位置是(i + m * k )% n。
(3) 然后用哈希表来记录谁被传到球了,如果传了两次,则跳出传球过程模拟。
(4) 最后遍历,如果哈希表中记录没有传到球,则压入结果数组当中。
2、相邻值的按位异或
2.1 题目链接
点击跳转到题目位置
2.2 题目描述
下标从 0 开始、长度为 n 的数组 derived 是由同样长度为 n 的原始 二进制数组 original 通过计算相邻值的 按位异或(⊕)派生而来。
特别地,对于范围 [0, n - 1] 内的每个下标 i :
如果 i = n - 1 ,那么 derived[i] = original[i] ⊕ original[0]
否则 derived[i] = original[i] ⊕ original[i + 1]
给你一个数组 derived ,请判断是否存在一个能够派生得到 derived 的 有效原始二进制数组 original 。
如果存在满足要求的原始二进制数组,返回 true ;否则,返回 false 。
二进制数组是仅由 0 和 1 组成的数组。
2.3 解题代码
class Solution {
public:bool doesValidArrayExist(vector<int>& derived) {int n = derived.size();vector<int> copy1(n);vector<int> copy2(n);copy1[0] = 1;for(int i = 1; i < n; ++i){copy1[i] = (copy1[i-1]^derived[i-1]);}if(derived[n-1] == (copy1[n-1] ^ copy1[0])){return true;}copy2[0] = 0;for(int i = 1; i < n; ++i){copy2[i] = (copy2[i-1]^derived[i-1]);}if(derived[n-1] == (copy2[n-1] ^ copy2[0])){return true;}return false;}
};
2.4 解题思路
(1) 这道题目的核心就在于倒推,给结果,能否知晓是由什么数组生成而来的。
(2) 根据规则,我们假设生成数组第一个元素分别为0和1可以倒推生成数组,判断生成得到的数组能否满足题目要求,这里用derived[n-1]来判断,因为这个数字与生成数组的第一个元素也有关系。
(3) 如果无论生成数组第一个元素是0还是1都不能得到最终的数组,那么就可以下判断不可能派生得到derived数组。
3、 矩阵中移动的最大次数
3.1 题目链接
点击跳转到题目位置
3.2 题目描述
给你一个下标从 0 开始、大小为 m x n 的矩阵 grid ,矩阵由若干 正 整数组成。
你可以从矩阵第一列中的 任一 单元格出发,按以下方式遍历 grid :
从单元格 (row, col) 可以移动到 (row - 1, col + 1)、(row, col + 1) 和 (row + 1, col + 1) 三个单元格中任一满足值 严格 大于当前单元格的单元格。
返回你在矩阵中能够 移动 的 最大 次数。
3.3 解题代码
class Solution {
public:int maxMoves(vector<vector<int>>& grid) {int m = grid.size();int n = grid[0].size();int dp[m][n];memset(dp, 0, sizeof(dp));for(int j = n-2; j >= 0; --j){for(int i = 0; i < m; ++i){int row = i;if(row - 1 >= 0){if(grid[row - 1][j + 1] > grid[i][j]){dp[i][j] = max(dp[i][j], dp[row - 1][j + 1] + 1);}}if(grid[i][j+1] > grid[i][j]){dp[i][j] = max(dp[i][j], dp[i][j+1] + 1);}if(row + 1 < m){if(grid[row + 1][j + 1] > grid[i][j]){dp[i][j] = max(dp[i][j], dp[row + 1][j + 1] + 1);}}}}int max0 = 0;for(int i = 0; i < m; ++i){max0 = max(max0, dp[i][0]);}return max0;}
};
3.4 解题思路
(1) 根据题目所描述的,这道题目的关键在于最终要求的是第一列元素所能移动的最大值。
(2) 我们又可以得出移动的方向永远是向着下一列,这代表着我们同一列的每一个元素的所在的位置的最大值只与后面一列的元素有关,即考虑使用动态规划来解决问题。
(3) 最终找出第一列的最大值即可。
4、 统计完全连通分量的数量
4.1 题目链接
点击跳转到题目位置
4.2 题目描述
给你一个整数 n 。现有一个包含 n 个顶点的 无向 图,顶点按从 0 到 n - 1 编号。给你一个二维整数数组 edges 其中 edges[i] = [ai, bi] 表示顶点 ai 和 bi 之间存在一条 无向 边。
返回图中 完全连通分量 的数量。
如果在子图中任意两个顶点之间都存在路径,并且子图中没有任何一个顶点与子图外部的顶点共享边,则称其为 连通分量 。
如果连通分量中每对节点之间都存在一条边,则称其为 完全连通分量 。
4.3 解题代码
class Solution {int Find(vector<int>& pre, int index){while(pre[index] != index){index = pre[index];}return index;}void Join(vector<int>& pre, int index1, int index2){index1 = Find(pre, index1);index2 = Find(pre, index2);if(index1 != index2){pre[index1] = index2;}}unordered_map<int, int> hash;unordered_map<int, int> point;
public:int countCompleteComponents(int n, vector<vector<int>>& edges) {int m = edges.size();vector<int> pre(100);for(int i = 0; i < n; ++i){pre[i] = i;}for(int i = 0; i < m; ++i){int x = edges[i][0]; int y = edges[i][1];Join(pre, x, y);}for(int i = 0; i < m; ++i){int x = edges[i][0];hash[Find(pre, x)]++;}for(int i = 0; i < n; ++i){point[Find(pre, i)]++;}int res = 0;for(int i = 0; i < n; ++i){if(i == pre[i]){if(hash[i] == (point[i] * (point[i] - 1)) / 2){res++;}}}return res;}
};
4.4 解题思路
(1) 这道题目是问有多少个完全通量,那么我们首先要知道有多少个子图。那么我们可以用并查集来统计有多少个子图。
(2) 我们将并查集中统领子图中的所有节点的节点所连接的边和所拥有的点的数量统计出来。
(3) 遍历所有子图,已知点的数量n,已知边的数量m,如果m 等于(n * n-1) / 2,那么完全通量+1即可。
打鸡血
心若在,梦就在,只不过是从头再来。哪怕每次周赛一题都做不出来,都得努力去研究,因为未来的某一天一定能够进步的。
相关文章:
)
LeetCode周赛复盘(第345场周赛)
文章目录 1、找出转圈游戏输家1.1 题目链接1.2 题目描述1.3 解题代码1.4 解题思路 2、相邻值的按位异或2.1 题目链接2.2 题目描述2.3 解题代码2.4 解题思路 3、 矩阵中移动的最大次数3.1 题目链接3.2 题目描述3.3 解题代码3.4 解题思路 4、 统计完全连通分量的数量4.1 题目链接…...

Call for Papers丨第三届GLB@KDD‘23 Workshop
鉴于介绍新数据集和Benchmark研究往往需要不同于常规论文的评审标准,计算机视觉和自然语言处理领域,以及最近的NeurIPS会议,都有专门致力于建立新Benchmark数据集和任务的Conference Track。然而在图机器学习领域,我们还没有类似的…...

【多线程】单例模式
目录 饿汉模式 懒汉模式-单线程版 懒汉模式-多线程版 懒汉模式-多线程版(改进) 单例是一种设计模式。 啥是设计模式 ? 设计模式好比象棋中的 " 棋谱 ". 红方当头炮 , 黑方马来跳 . 针对红方的一些走法 , 黑方应招的时候有一些固定的套路. 按照套路来走局势…...
7搜索管理
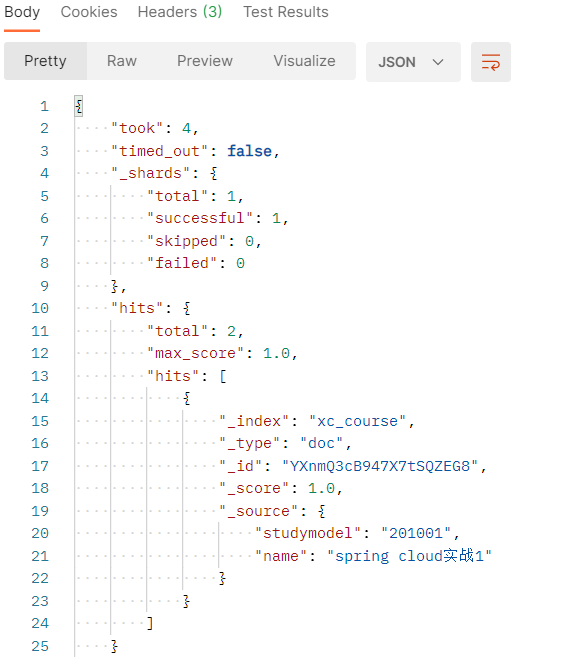
7搜索管理 7.1 准备环境 7.1.1 创建映射 创建xc_course索引库。 创建如下映射 post:http://localhost:9200/xc_course/doc/_mapping 参考 “资料”–》搜索测试-初始化数据.txt { "properties": { "description": { "type": &…...

在Pytorch中使用Tensorboard
Tensorboard是一款深度学习可视化软件,目前主要使用了它的可视化模型, 可视化模型权重和可视化损失函数功能。 x.1 tensorboard初始化 tensorboard初始化需要导入SummaryWriter包并指定存储位置和开放端口号。 from torch.utils.tensorboard import SummaryWrite…...
[笔记]深入解析Windows操作系统《四》管理机制
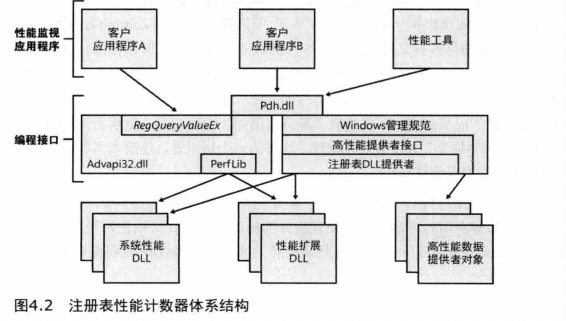
文章目录 前言4.1注册表查看和修改注册表注册表用法注册表数据类型注册表逻辑结构HKEY_CURRENT_USERHKEY_USERS 实验:观察轮廓加载和卸载HKEY_CLASSES_ROOTHKEY_LOCAL_MACHINE 实验:离线方式或远程编辑BCDHKEY_CURRENT_CONFIGHKEY_PERFORMANCE_DATA 前言 本章讲述了…...
【小沐学Python】Python实现在线英语翻译功能
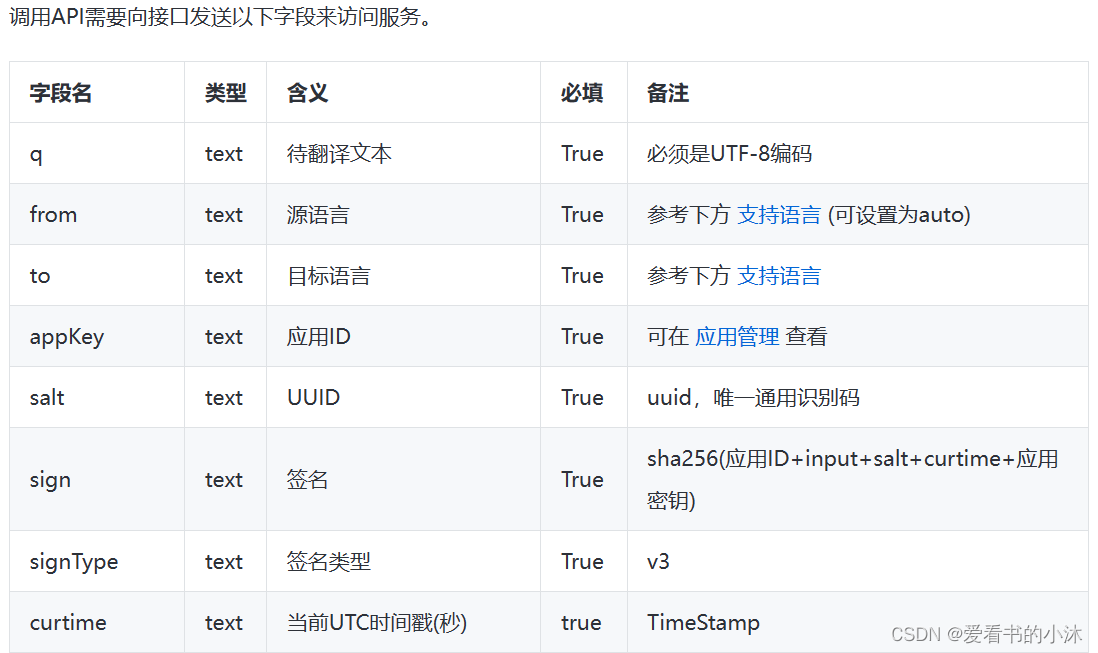
文章目录 1、简介2、在线翻译接口2.1 Google Translate API2.2 Microsoft Translator API2.2.1 开发简介2.2.2 开发费用2.2.3 开发API 2.3 百度翻译开放平台 API2.3.1 开发简介2.3.2 开发费用2.3.3 开发API 2.4 Tencent AI 开放平台的翻译 API2.4.1 开发简介2.4.2 开发API 2.5 …...

k8s中pod使用详解
一、前言 在之前k8s组件一篇中,我们谈到了pod这个组件,了解到pod是k8s中资源管理的最小单位,可以说Pod是整个k8s对外提供服务的最基础的个体,有必要对Pod做深入的学习和探究。 二、再看k8s架构图 为了加深对k8s中pod的理解,再来回顾下k8s的完整架构 三、pod特点 结合上面这…...
案例说明:vue中Element UI下拉列表el-option中的key、value、label含义各是什么
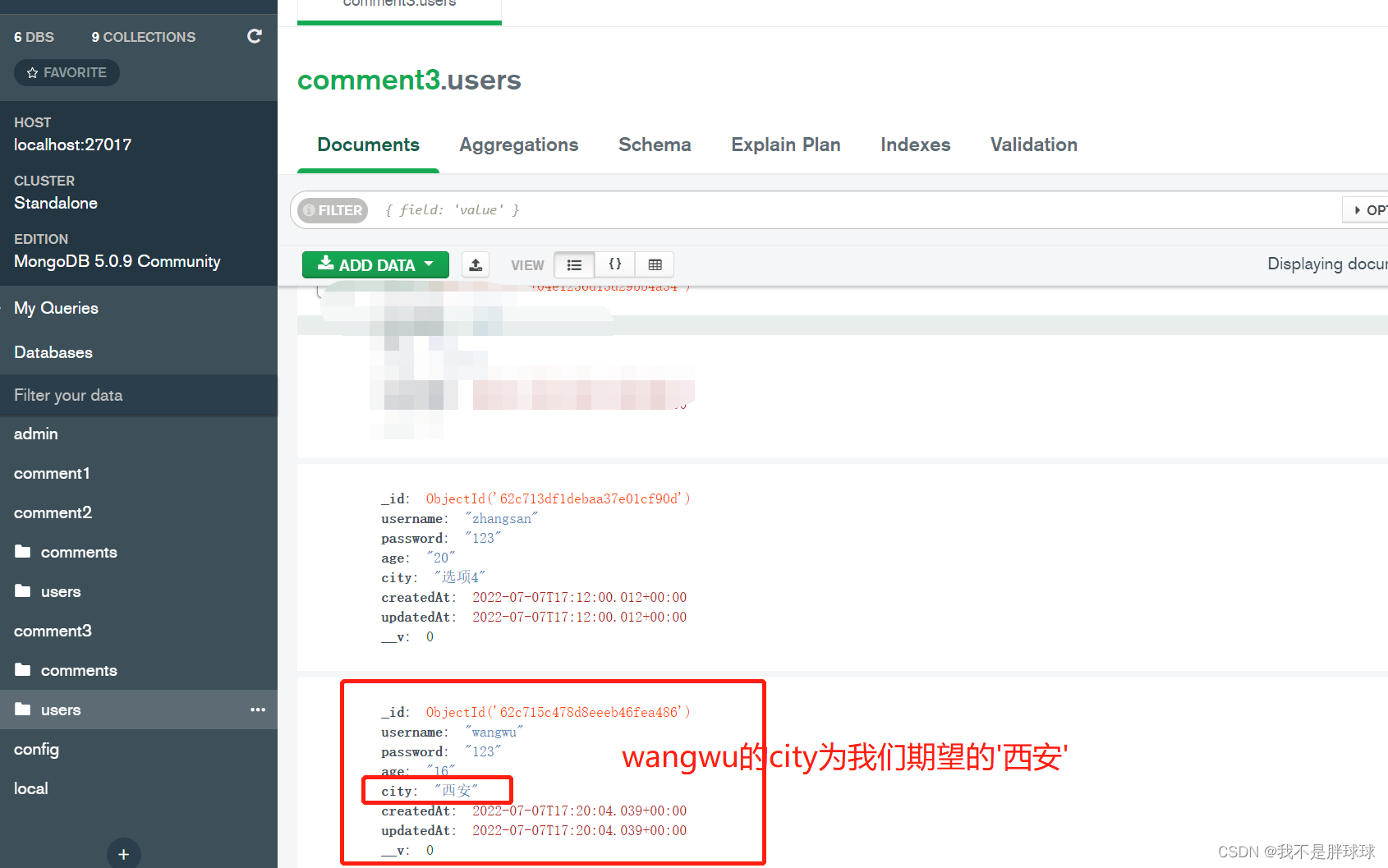
可以简单理解为:label 是给用户展示的东西,value是前端往后端传递的真实值 <template><div><el-page-header back"goBack" content"注册"></el-page-header><el-divider></el-divider><el-…...
idea创建javaweb项目步骤超详细(2022最新版本)
目录 前言必读 一、新建文件 1.在idea里面点击文件-新建-项目 2.新建项目-更改名称为自己想要的项目名称-创建 3.右键自己建立的项目-添加框架支持(英文版是Add Framework Support...) 4.勾选Web应用程序-确定 5.建立成功界面 二、配置tomcat 6.…...

「SAP ABAP」OPEN SQL(六)【DELETE语句 | MODIFY语句】
💂作者简介: THUNDER王,一名热爱财税和SAP ABAP编程以及热爱分享的博主。目前于江西师范大学本科在读,同时任汉硕云(广东)科技有限公司ABAP开发顾问。在学习工作中,我通常使用偏后端的开发语言ABAP,SQL进行任务的完成,对SAP企业管理系统,SAP ABAP开发和数据库具有较…...

SpringCloud --- Feign远程调用
一、RestTemplate问题 先来看我们以前利用RestTemplate发起远程调用的代码: 存在下面的问题: 代码可读性差,编程体验不统一参数复杂URL难以维护 Feign是一个声明式的http客户端,官方地址:GitHub - OpenFeign/feign:…...
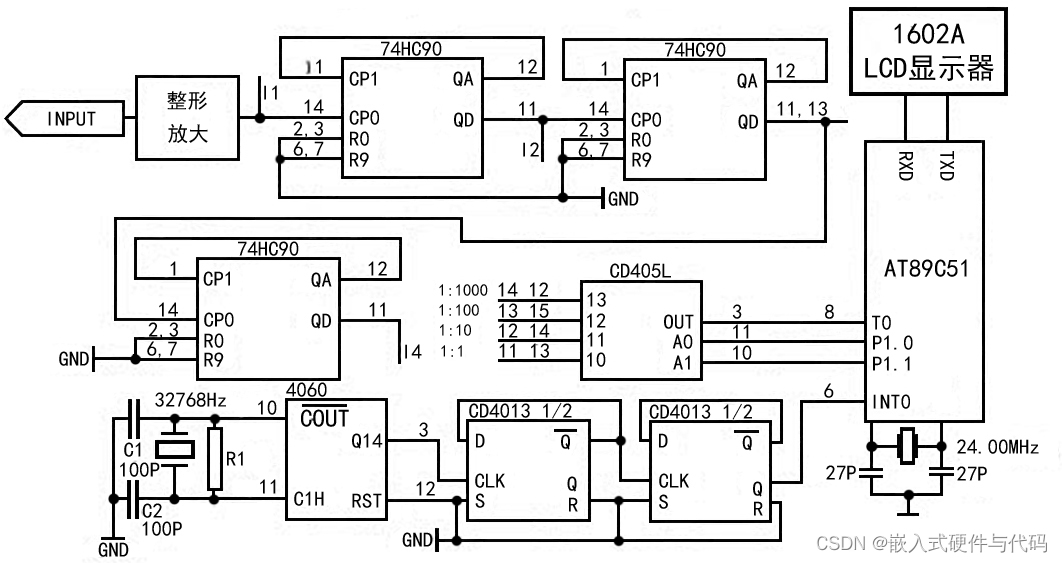
基于单片机的数字频率计设计
数字频率计概述 数字频率计是计算机、通讯设备、音频视频等科研生产领域不可缺少的测量仪器。它是一种用十进制数字显示被测信号频率的数字测量仪器。它的基本功能是测量正弦信号,方波信号及其他各种单位时间内变化的物理量。在进行模拟、数字电路的设计、安装、调试…...
我看看哪个靓仔还没把Github Copilot用起来?
本人经常分享有价值的生产力工具、技术、好物与书籍,可关注同名公众🐭并设为🌟星标,第一时间获得更新 Github Copilot 是一个AI编程助手,其使用 OpenAI CodeX 在你的编辑器中实时建议代码或给你实现整个功能。 视频版介…...

C++系列一: C++简介
C入门简介 1. C语言的特点2. C编译器3. 第一个 C 程序4. 总结(手稿版) C 是一种高级编程语言,是C语言的扩展和改进版本,由Bjarne Stroustrup于1983年在贝尔实验室为了支持C语言中的面向对象编程而创建。C 既能够进行底层的系统编程…...

信通初试第一:无科研无竞赛一战上岸上海交大819学硕感悟
笔者来自通信考研小马哥23上交819全程班学员 信通初试第一:无科研无竞赛一战上岸上海交大819学硕感悟 原创2023-04-27 11:04通信考研小马哥 笔者来自通信考研小马哥23上交819全程班学员 本人情况: 本人是19届交本,本科成绩很差,…...

Spring —— Spring Boot 配置文件
JavaEE传送门 JavaEE Spring —— Bean 作用域和生命周期 Spring —— Spring Boot 创建和使用 目录 Spring Boot 配置文件Spring Boot 配置文件格式properties配置文件properties 基本语法properties 缺点 yml 配置文件yml 基本语法yml 配置不同类型数据及 nullyml 配置对象…...
Python 网络爬虫与数据采集(一)
Python 网络爬虫与数据采集 第1章 序章 网络爬虫基础1 爬虫基本概述1.1 爬虫是什么1.2 爬虫可以做什么1.3 爬虫的分类1.4 爬虫的基本流程1.4.1 浏览网页的流程1.4.2 爬虫的基本流程 1.5 爬虫与反爬虫1.5.1 爬虫的攻与防1.5.2 常见的反爬与反反爬 1.6 爬虫的合法性与 robots 协议…...

2023年6月DAMA-CDGP数据治理专家认证请尽快报名啦!
目前6月DAMA-CDGP数据治理认证考试开放报名地区有:北京、上海、广州、深圳、长沙、呼和浩特。 目前南京、济南、西安、杭州等地区还在接近开考人数中,打算参加6月考试的朋友们可以抓紧时间报名啦!!! 5月初,…...
STM32+esp8266,让你的STM32开发板连接网络-----esp8266
分享一下,STM32开发板连接网络的第一种方法:连接esp8266。 esp8266与STM32利用串口通信连接,esp8266连接网络,把收到的数据通过串口的方式传输给STM32,之后STM32接收到消息做出对应的反应。 使用到的开发板如图&…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...
