[刷题]贪心入门
文章目录
- 贪心
- 区间问题
- 区间选点
- 区间合并
- 区间覆盖
- 哈夫曼树(堆)
- 合并果子
- 排序不等式
- 排队打水
- 绝对值不等式
- 货仓选址
- 推出来的不等式
- 耍杂技的牛
- 以前的题
贪心
贪心:每一步行动总是按某种指标选取最优的操作来进行, 该指标只看眼前,并不考虑以后可能造成的影响。
局部最优 → 整体最优。
区间问题
区间选点
给定 N 个闭区间 [ai,bi][ai,bi],请你在数轴上选择尽量少的点,使得每个区间内至少包含一个选出的点。
输出选择的点的最小数量。
位于区间端点上的点也算作区间内。
输入格式
第一行包含整数 N,表示区间数。
接下来 N 行,每行包含两个整数 ai,bi,表示一个区间的两个端点。
输出格式
输出一个整数,表示所需的点的最小数量。
数据范围
1≤N≤105,
−109≤ai≤bi≤109
此题同理:最大不相交区间数量
给定 NN 个闭区间 [ai,bi][ai,bi],请你在数轴上选择若干区间,使得选中的区间之间互不相交(包括端点)。
思路:
右端点排序,直接对比。下面是题解
左端点排序的话,逆序对比。
#include<iostream>
#include<algorithm>
using namespace std;const int N = 1e5+10;
pair<int,int> v[N];
bool cmp(pair<int,int> a,pair<int,int> b)
{return a.second<b.second;
}
int main(void)
{int n;scanf("%d",&n);for(int i=0;i<n;i++)cin>>v[i].first>>v[i].second;sort(v,v+n,cmp);int res = 0,ed = -2e9;for(int i=0;i<n;i++){if(v[i].first>ed) {res++;ed = v[i].second;}}cout<<res;
}
区间合并
给定 N 个闭区间 [ai,bi][ai,bi],请你将这些区间分成若干组,使得每组内部的区间两两之间(包括端点)没有交集,并使得组数尽可能小。
输出最小组数。
输入格式
第一行包含整数 N,表示区间数。
接下来 N 行,每行包含两个整数 ai,bi,表示一个区间的两个端点。
输出格式
输出一个整数,表示最小组数。
数据范围
1≤N≤105,
−109≤ai≤bi≤109
左端点排序:
1.逻辑解释:
当第cnt个区间的左端点小于前cnt - 1个区间的最小的max_r时,前cnt -1个区间的左端点不一定都小于第cnt个区间的左端点,因为是按照右端点排序的。如果有些区间的左端点大于第cnt个区间的左端点,并且大于另一些区间的max_r,就不能保证这cnt个区间都有一个共同点(就是第cnt个区间的左端点)。
2.反证解释:
按照右边排序的话,各个区间的左端点不能保证单调性,所以有可能第三个区间的左端点比第一个区间的左端点还要左边,它可以特别长。
反例: [1, 3], [2, 5], [4, 100], [10, 13]
3.比喻:
比如,有n个人需要用教室,每个人占用教室的起始时间和终止时间是不一样的。
1、如果想知道只有一间教室,能安排下的最多不冲突人数(不是所有的人都有机会,有的会被舍掉)是多少(区间选点和最大不相交问题),那么当然是最先结束的人排在前面,这样后面的人才有更多机会。如果是按左端点排序,那么如过一个人0点开始用,那么肯定他排在最前面,但是如果他自己就占用了24小时,那么只能给他一个人用了,这样就达不到最大的效果。所以按左端点排序。
2、如果想知道这些人都必须安排,没有人被舍弃,至少需要多少个教室能安排下(区间分组问题)。那么肯定是按照开始时间排序,开始时间越早越优先。这样每间教室都能得到最充分的利用。
偷偷说:实际按左右无所谓的。这题的区间只是一个一维坐标系,如果要按右端点排序,那你就从右往左找 min_r 好了。只是一个方向问题。
思路:
1.将所有区间按左端点从小到大排序
2.从前往后判断 : if L[i] > Max_r ,即是否能将其放到某个现有的组中
①如果存在,将其放进去,并更新当前组的 MAX_r
②如果不存在,开新组,然后再将其放进去
#include <iostream>
#include <algorithm>
#include <queue>using namespace std;const int N = 100010;int n;
struct Range
{int l, r;bool operator< (const Range &W)const{return l < W.l;}
}range[N];int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ ){int l, r;scanf("%d%d", &l, &r);range[i] = {l, r};}sort(range, range + n);priority_queue<int, vector<int>, greater<int>> heap;for (int i = 0; i < n; i ++ ){//小根堆里存的是每个分组的最大右端点,//当前要判断的区间的左端点至少要大于其中一个分组的最大右端点,才会用更新替代开新组。auto it = range[i];if (heap.empty() || heap.top() >= it.l) heap.push(it.r); //开新组else{heap.pop(); //不开组,更新当前组的MAX_r。heap.push(it.r);}}printf("%d\n", heap.size());return 0;
}区间覆盖
给定 N 个闭区间 [ai,bi][ai,bi] 以及一个线段区间 [s,t][s,t],请你选择尽量少的区间,将指定线段区间完全覆盖。
输出最少区间数,如果无法完全覆盖则输出 −1。
输入格式
第一行包含两个整数 s 和 t,表示给定线段区间的两个端点。
第二行包含整数 N,表示给定区间数。
接下来 N 行,每行包含两个整数 ai,bi,表示一个区间的两个端点。
输出格式
输出一个整数,表示所需最少区间数。
如果无解,则输出 −1。
数据范围
1≤N≤105,
−109≤ai≤bi≤109,
−109≤s≤t≤109
思路:
1.从左到右按左端点排序
2.从前往后依次枚举每个区间,在所有能覆盖start的区间中,选择右端点最大的区间,
然后将start更新成右端点最大值
#include <iostream>
#include <algorithm>using namespace std;const int N = 100010;int n;
struct Range
{int l, r;bool operator< (const Range &W)const{return l < W.l;}
}range[N];int main()
{int st, ed;scanf("%d%d", &st, &ed);scanf("%d", &n);for (int i = 0; i < n; i ++ ){int l, r;scanf("%d%d", &l, &r);range[i] = {l, r};}sort(range, range + n);int res = 0;bool success = false;for (int i = 0; i < n; i ++ ){int j = i, r = -2e9;while (j < n && range[j].l <= st){r = max(r, range[j].r);j ++ ;}if (r < st){res = -1;break;}res ++ ;if (r >= ed){success = true;break;}st = r;i = j - 1;}if (!success) res = -1;printf("%d\n", res);return 0;
}Q :最后为什么是i=j-1 而不是i=j ?
A :比如说: j扫描到了 2 此时while() 退出了 我们下次 i 应该从 2开始但是需要注意的是我们的for()循环 i++ ,i还会加1次 此时 我们的 i=3 直接从 3 开始循环了,故需要减1。
Q :那为什么不把i++去掉,然后i = j好理解一点
A :因为j不一定会++,这样可能会死循环
哈夫曼树(堆)
合并果子
在一个果园里,达达已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。
达达决定把所有的果子合成一堆。
每一次合并,达达可以把两堆果子合并到一起,消耗的体力等于两堆果子的重量之和。
可以看出,所有的果子经过 n−1n−1 次合并之后,就只剩下一堆了。
达达在合并果子时总共消耗的体力等于每次合并所耗体力之和。
因为还要花大力气把这些果子搬回家,所以达达在合并果子时要尽可能地节省体力。
假定每个果子重量都为 11,并且已知果子的种类数和每种果子的数目,你的任务是设计出合并的次序方案,使达达耗费的体力最少,并输出这个最小的体力耗费值。
例如有 33 种果子,数目依次为 1,2,91,2,9。
可以先将 1、21、2 堆合并,新堆数目为 33,耗费体力为 33。
接着,将新堆与原先的第三堆合并,又得到新的堆,数目为 1212,耗费体力为 1212。
所以达达总共耗费体力=3+12=15=3+12=15。
可以证明 15 为最小的体力耗费值。
输入格式
输入包括两行,第一行是一个整数 n,表示果子的种类数。
第二行包含 n 个整数,用空格分隔,第 i 个整数 ai 是第 i种果子的数目。
输出格式
输出包括一行,这一行只包含一个整数,也就是最小的体力耗费值。
输入数据保证这个值小于 231。
数据范围
1≤n≤10000,
1≤ai≤20000
#include<iostream>
#include<queue>
using namespace std ;
int res;
int main(void)
{priority_queue<int,vector<int>,greater<int> > heap;int n;cin>>n;while(n--) {int x ;scanf("%d",&x);heap.push(x);}while(heap.size()>1){int a = heap.top();heap.pop();int b = heap.top();heap.pop();res += a+b;heap.push(a+b);}printf("%d",res);}
排序不等式
排队打水
有 n 个人排队到 11 个水龙头处打水,第 ii 个人装满水桶所需的时间是 ti,请问如何安排他们的打水顺序才能使所有人的等待时间之和最小?
输入格式
第一行包含整数 n。
第二行包含 n 个整数,其中第 i 个整数表示第 i 个人装满水桶所花费的时间 ti。
输出格式
输出一个整数,表示最小的等待时间之和。
数据范围
1≤n≤105,
1≤ti≤104
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e5+10;
long long res;
int main(void)
{int a[N],n;cin>>n;for(int i = 0;i<n;i++){cin>>a[i];}sort(a,a+n);for(int i=0;i<n;i++){res += a[i]*(n-1-i);}cout<<res;
}
绝对值不等式
货仓选址
在一条数轴上有 N 家商店,它们的坐标分别为 A1∼AN。
现在需要在数轴上建立一家货仓,每天清晨,从货仓到每家商店都要运送一车商品。
为了提高效率,求把货仓建在何处,可以使得货仓到每家商店的距离之和最小。
输入格式
第一行输入整数 N。
第二行 N 个整数 A1∼AN。
输出格式
输出一个整数,表示距离之和的最小值。
数据范围
1≤N≤1000001≤N≤100000,
0≤Ai≤40000
#include<iostream>
#include<algorithm>
using namespace std ;
const int N = 1e5+10;
int n;
int a[N];
int res;
int main(void)
{scanf("%d",&n);for(int i=0;i<n;i++){scanf("%d",&a[i]);}sort(a,a+n);for(int i=0;i<n;i++){res += abs(a[i]-a[n/2]);}cout<<res;
}推出来的不等式
耍杂技的牛
农民约翰的 N 头奶牛(编号为1…N)计划逃跑并加入马戏团,为此它们决定练习表演杂技。
奶牛们不是非常有创意,只提出了一个杂技表演:
叠罗汉,表演时,奶牛们站在彼此的身上,形成一个高高的垂直堆叠。
奶牛们正在试图找到自己在这个堆叠中应该所处的位置顺序。
这 N 头奶牛中的每一头都有着自己的重量 Wi 以及自己的强壮程度 Si。
一头牛支撑不住的可能性取决于它头上所有牛的总重量(不包括它自己)减去它的身体强壮程度的值,现在称该数值为风险值,风险值越大,这只牛撑不住的可能性越高。
您的任务是确定奶牛的排序,使得所有奶牛的风险值中的最大值尽可能的小。
输入格式
第一行输入整数 N,表示奶牛数量。
接下来 N 行,每行输入两个整数,表示牛的重量和强壮程度,第 i 行表示第 i 头牛的重量 Wi 以及它的强壮程度 Si。
输出格式
输出一个整数,表示最大风险值的最小可能值。
数据范围
1≤N≤50000,
1≤Wi≤10,000,
1≤Si≤1,000,000,000
既然是推出来的不等式,下面来贴下推理过程:
/ 交换前 交换后 第i头牛 W1+W2+…W(i-1) - Si W1+…Wi-1+Wi+1 - Si 第i+1头牛 W1+W2+…Wi - S(i+1) W1+…Wi-1 - S(i+1) 去掉重复的W1+…W(i-1) , 得
/ 交换前 交换后 第i头牛 - Si Wi+1 - Si 第i+1头牛 Wi - S(i+1) - S(i+1) 题目所求答案为危险系数最大值的最小值,所以找到最大值就OK。
对于上表,易知 Wi -S(i+1) > -S(i+1) , Wi+1-Si > -Si ;
故交换前取最大值 Wi -S(i+1) ,交换后去最大值 Wi+1-Si 。
假设交换后,我们得到的是最小值(这样假设得到的式子能够帮助我们求得答案),则有不等式:
Wi - S(i+1) > Wi+1 - Si ,即交换后变小。
移项得 Wi + Si > Wi+1 + Si+1 。
此时我们发现,设 Q = W+S ,只需要按照Q对输入排序(也就是完成交换的过程),再依次比较。
取Q1 … Qi 中的最小值即可。
#include <iostream>
#include <algorithm>using namespace std;typedef pair<int, int> PII;const int N = 50010;int n;
PII cow[N];int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ ){int s, w;scanf("%d%d", &w, &s);cow[i] = {w + s, w};}sort(cow, cow + n);int res = -2e9, sum = 0;for (int i = 0; i < n; i ++ ){int s = cow[i].first - cow[i].second, w = cow[i].second;res = max(res, sum - s);sum += w;}printf("%d\n", res);return 0;
}
以前的题
圣诞节来临了,圣诞老人准备分发糖果,现
在有多箱不同的糖果,每箱糖果有自己的价值和重
量,每箱糖果都可以拆分成任意散装组合带走。圣
诞老人的驯鹿雪橇最多只能装下重量W的糖果,请
问圣诞老人最多能带走多大价值的糖果。
#include<iostream>
#include<algorithm>
#include<memory.h>
#include<iomanip>
const double eps = 1e-6;
using namespace std;
int W;
double V;
struct suger{int w;int v;bool operator<(const suger& s){return double(v)/w-double(s.v)/s.w>eps;}
}sugers[110];
void greedy(int &total,int &n){for(int i=0;i<n;i++){if(total+sugers[i].w<=W){total += sugers[i].w;V += sugers[i].v;}else {V += sugers[i].v* double(W-total)/sugers[i].w; W = W+W-total;break;}}
}
int main(void)
{int n,total=0;cin>>n>>W;for(int i=0;i<n;i++){cin>>sugers[i].v>>sugers[i].w;}sort(sugers,sugers+n);//自己写greedy(total,n);cout<<fixed<<setprecision(1)<<V;}
各地放了多部电影 ,给定每部电影的放映时间区间,区间重叠的电影不可能同时
看(端点可以重合),问李雷最多可以看多少部电影。
int total;
struct film{int s;int e;bool operator<(const film& f){return e<f.e;}
}f,films[110];
int main(void)
{ int n;cin>>n;for(int i=0;i<n;i++){cin>>films[i].s>>films[i].e;}sort(films,films+n);total++;f=films[0];for(int i=1;i<n;i++){if(f.e<=films[i].s){total++;f=films[i];}}cout << endl<<total;
}有 n头牛(1<=n<=50,000)要挤奶。给定每头牛挤奶的时间区
间[A,B] (1<=A<=B<=1,000,000,A,B为整数)。
牛需要呆畜栏里才能挤奶。一个畜栏同一时间只能容纳一头牛。
问至少需要多少个畜栏,才能完成全部挤奶工作,以及每头牛都
放哪个畜栏里(Special judged)
去同一个畜栏的两头牛,它们挤奶时间区间哪怕只在端点重合也
是不可以的。
//难点:优先队列的运用 + 配合贪心和队列的排序
//(奶牛和栅栏的顺序定义operator,栅栏和奶牛都需要no来记录原顺序编号)
#include<iostream> //(因为它们都被排序打乱了 )
#include<algorithm> //ps:循环均为从1开始
#include<queue>
using namespace std;
struct cow{int s;//时间区间 start -end int e;int no; //奶牛编号:防止原奶牛顺序 由于进入时间的排序而被打乱 operator<(const cow& c){ //排序 return s<c.s;}
}cows[100];
int pos[100];
typedef struct fence{int e;//栅栏的结束时间不断在变 ,作为队列排序依据int no; //栅栏编号,方便记录奶牛进入的栅栏(同样是防止队列顺序更新而失去原顺序编号) bool operator<(const fence & f) const {return e > f.e; }fence(int e,int n):e(e),no(n){};// 对栅栏赋值。
}fen;
int total; //栅栏数
int main(void)
{ //1.奶牛赋值+排序 int n;cin>>n;for(int i=1;i<=n;i++){cin>>cows[i].s>>cows[i].e;cows[i].no=i;//排序前,在赋值no过程记录好原位置 }sort(cows+1,cows+n+1); //2.栅栏赋值+排序 priority_queue<fen> pq;for(int i=1;i<=n;i++){ if(pq.empty()){//情况1.最开始(无奶牛) ++total;pq.push(fen(cows[i].e,total));pos[cows[i].no]=total;}else { //情况2. next奶牛与目前栅栏冲突 fen f=pq.top();//利用排序(目前结束最快) 找到待命栅栏 if(f.e>=cows[i].s){++total;pq.push(fen(cows[i].e,total)); //冲突加入新栅栏,编号即total pos[cows[i].no]=total;}else {//情况3. 不冲突 //不冲突:total不变,队列弹出原奶牛,压入新奶牛 pq.pop(); pos[cows[i].no]=f.no; //进入编号为top(待命)的栅栏 pq.push(fen(cows[i].e,f.no)); //不冲突使用原栅栏}}}//3.循环结束,事件结束,输出 cout<< total<<endl;for(int i=1;i<=n;i++)cout<<pos[i]<<endl;
}[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YwPjrjKm-1684146461476)(data:image/gif;base64,R0lGODlhAQABAPABAP///wAAACH5BAEKAAAALAAAAAABAAEAAAICRAEAOw==)]
放置雷达:
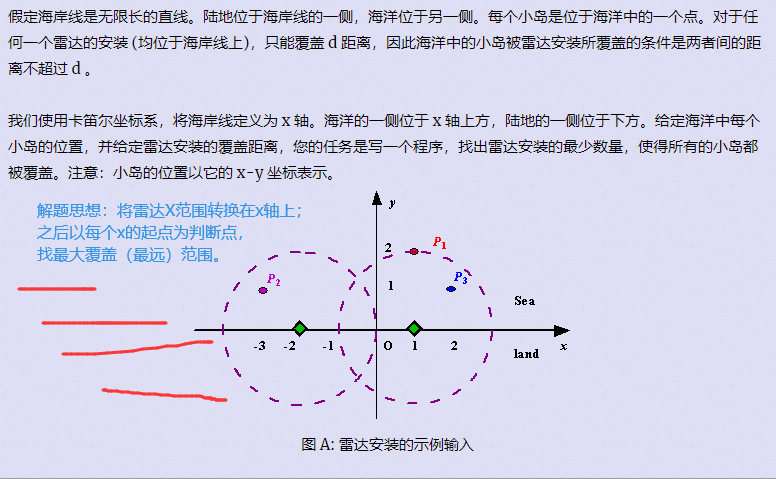 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-k2PNb52e-1684146461477)(data:image/gif;base64,R0lGODlhAQABAPABAP///wAAACH5BAEKAAAALAAAAAABAAEAAAICRAEAOw==)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-k2PNb52e-1684146461477)(data:image/gif;base64,R0lGODlhAQABAPABAP///wAAACH5BAEKAAAALAAAAAABAAEAAAICRAEAOw==)]
#include<iostream>
#include<vector>
#include<cmath>
#include<algorithm>
using namespace std;
int n,d,total;
class how{public:bool operator()(pair<double,double> p1,pair<double,double> p2){return p1.first<p2.first;}
};
bool decide(vector<pair<double,double> > m,int F,int i)
{for(int k=F;k<i;k++){if(m[i].first<=m[k].second&&m[i].first>=m[k].first)continue;else return false;}return true;}
void dfs(const vector<pair<double,double> >&m)
{int FNC=0;while(1){ int i;for(i=FNC+1;i<n;i++){ if(decide(m,FNC,i)) continue;else{FNC=i;total++;break;}} if(i>=n) {total++;break;}}}
int flag=1;
int main(void)
{ while(cin>>n>>d&&n!=0){total=0;vector<pair<double,double> > m;for(int i=0;i<n;i++){int x,y;cin>>x>>y;pair<double,double> p;p.first =x-sqrt(d*d-y*y);p.second=x+sqrt(d*d-y*y);m.push_back(p);}sort(m.begin(),m.end(),how());dfs(m);cout<<"case"<<flag<<":"<<total<<endl;flag++;}
} 相关文章:

[刷题]贪心入门
文章目录 贪心区间问题区间选点区间合并区间覆盖 哈夫曼树(堆)合并果子 排序不等式排队打水 绝对值不等式货仓选址 推出来的不等式耍杂技的牛 以前的题 贪心 贪心:每一步行动总是按某种指标选取最优的操作来进行, 该指标只看眼前&…...
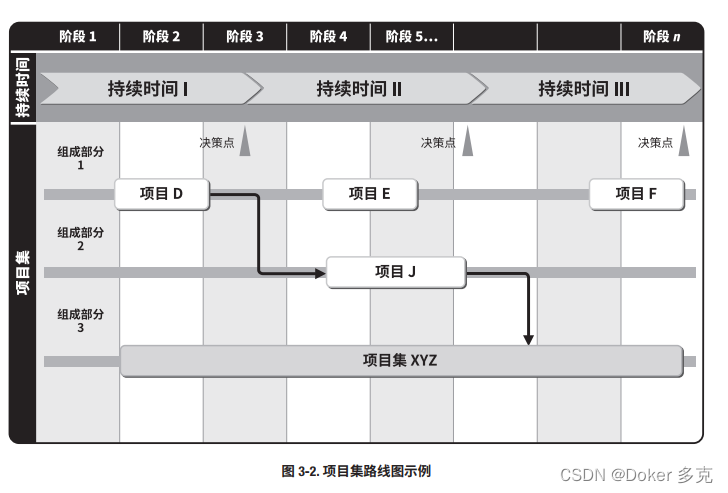
项目集战略一致性
项目集战略一致性是识别项目集输出和成果,以便与组织的目标和目的保持一致的绩效领域。 本章内容包括: 1 项目集商业论证 2 项目集章程 3 项目集路线图 4 环境评估 5 项目集风险管理战略 项目集应与组织战略保持一致,并促进组织效益的实现。为…...
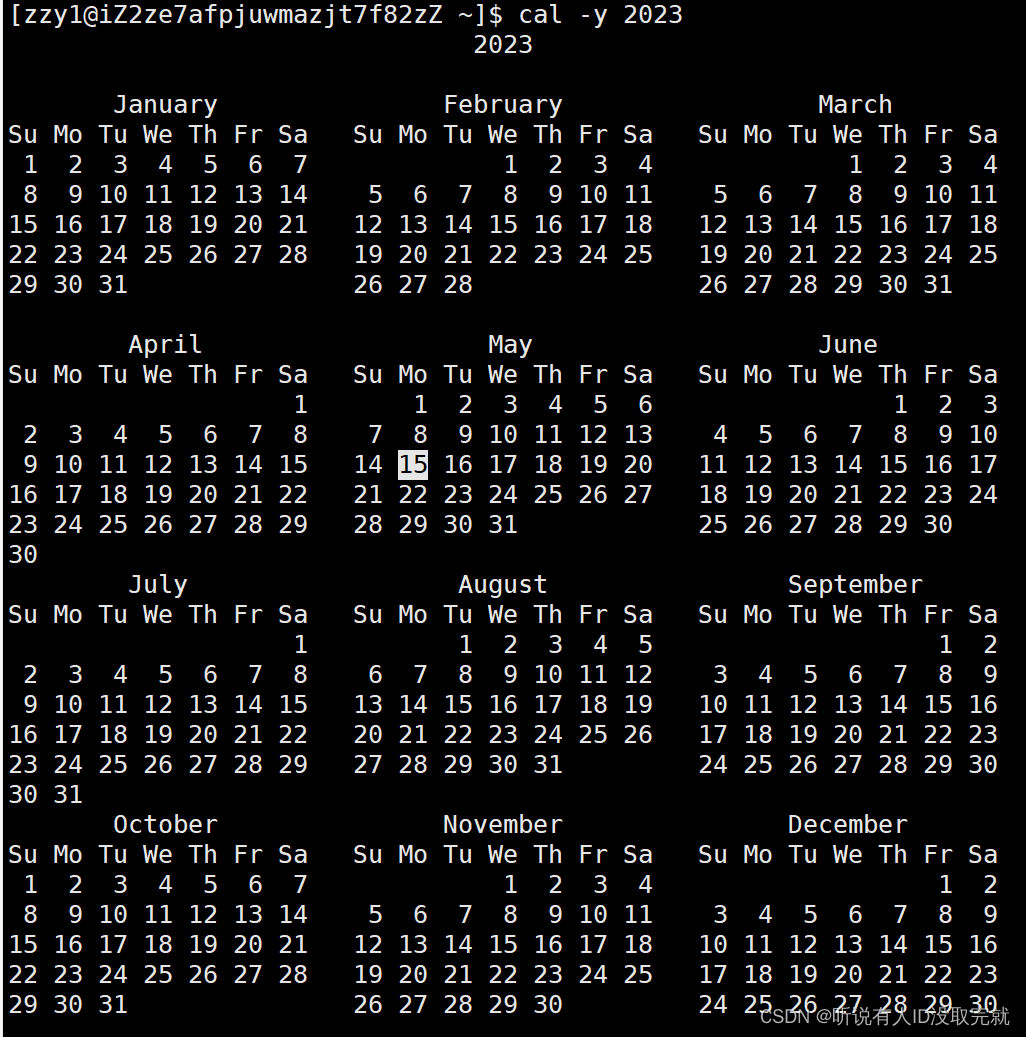
Linux学习 Day3
目录 1. 时间相关的指令 2. cal指令 3. find指令:(灰常重要) -name 4. grep指令 5. zip/unzip指令 6. tar指令(重要):打包/解包,不打开它,直接看内容 7. bc指令 8. uname –…...

前端开发推荐vscode安装什么插件?
前言 可以参考一下下面我推荐的插件,注意:插件的目的是用于提高开发的效率,节约开发的时间,像类似检查一些bug、拼写错误等这些可以使用插件快速的识别,避免在查找错误上浪费过多的时间,但切记不要过度依赖…...

如何打造完整的客户服务体系?
对于企业来说,提供优质的客户服务是保持竞争力和赢得市场份额的关键因素之一。一个高效、专业、人性化的客户服务体系,对于企业吸引和留住客户,提升品牌声誉,甚至增加销售额都有着不可忽视的作用。本文将从多个方面来阐述如何打造…...

裸奔时代,隐私何处寻?
随着互联网的普及,人工智能时代的大幕初启,数据作为人工智能的重要支撑,数据之争成为“兵家必争之地”,随之而来的就是,各种花式手段“收割”个人信息,用户隐私暴露程度越来越高,隐私保护早已成…...
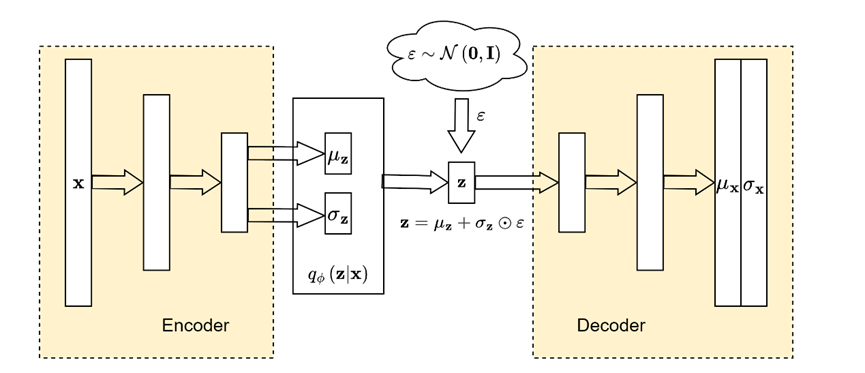
从期望最大化(EM)到变分自编码器(VAE)
本文主要记录了自己对变分自编码器论文的理解。 Kingma D P, Welling M. Auto-encoding variational bayes[J]. arXiv preprint arXiv:1312.6114, 2013. https://arxiv.org/abs/1312.6114 1 带有潜在变量的极大似然估计 假设我们有一个有限整数随机数发生器 z ∼ p θ ( z ) …...

【数学杂记】表达式中的 s.t. 是什么意思
今天写题的时候遇见了这个记号:s.t.,查了一下百度。 s.t.,全称 subject to,意思是“使得……满足”。 比如这个: 意思是存在 i i i,使得 i i i 满足 A i ≠ B i A_i\neq B_i AiBi. 运用这个记号…...

flink watermark介绍及watermark的窗口触发机制
Flink的三种时间 在谈watermark之前,首先需要了解flink的三种时间概念。在flink中,有三种时间戳概念:Event Time 、Processing Time 和 Ingestion Time。其中watermark只对Event Time类型的时间戳有用。这三种时间概念分别表示: …...

Spring Cloud: 云原生微服务实践
文章目录 1. Spring Cloud 简介2. Spring Cloud Eureka:服务注册与发现在Spring Cloud中使用Eureka 3. Spring Cloud Config:分布式配置中心在Spring Cloud中使用Config 4. Spring Cloud Hystrix:熔断器在Spring Cloud中使用Hystrix 5. Sprin…...

存bean和取bean
准备工作存bean获取bean三种方式 准备工作 bean:一个对象在多个地方使用。 spring和spring boot:spring和spring boot项目;spring相当于老版本 spring boot本质还是spring项目;为了方便spring项目的搭建;操作起来更加简单 spring…...

39. 组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。 candidates 中的 同一个 数字可以 无限制重复被选取 。如…...

100行以内Python能做那些事
Python100 找到一个很好的python教程分享出来---->非本人 B站视频连接 100行以内的Pyhton代码可以做哪些有意思的事 按照难度1-5颗星,分为五个文件夹 希望大家可以补充 关于运行环境的补充 Python3.7 Pycharm社区版2019 关于用到的Python库,有些是自带的&am…...

Android 电源键事件流程分析
Android 电源键事件流程分析 电源按键流程处理逻辑在 PhoneWindowManager.java类中的 dispatchUnhandledKey 方法中 frameworks/base/services/core/java/com/android/server/policy/PhoneWindowManager.java从dispatchUnhandledKey方法开始分析 Overridepublic KeyEvent dis…...

游戏搬砖简述-1
游戏搬砖是一种在游戏中通过重复性的任务来获取游戏内货币或物品的行为。这种行为在游戏中非常普遍,尤其是在一些MMORPG游戏中。虽然游戏搬砖看起来很无聊,但是它确实是一种可以赚钱的方式,而且对于一些玩家来说,游戏搬砖也是一种…...

多线程基础总结
1. 为什么要有多线程? 线程:线程是操作系统能够进行运算调度的最小单位。它被包含在进程之中,是进程中实际运行单位。 进程:进程是程序的基本执行实体。 什么是多线程? 有了多线程,我们就可以让程序同时做…...
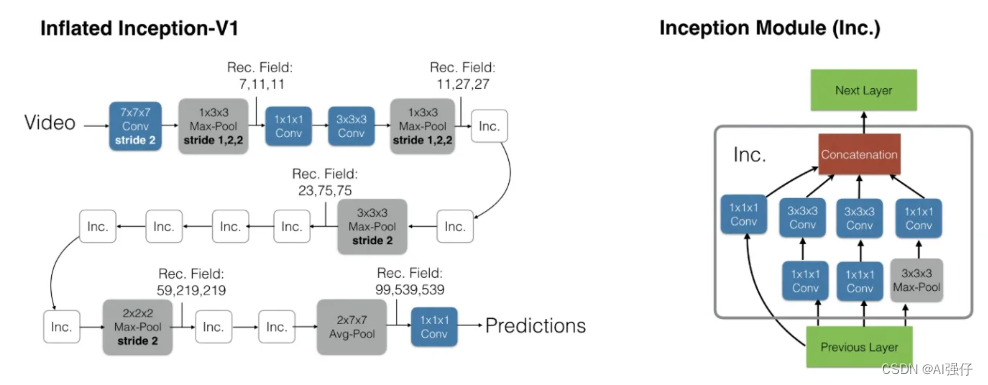
视频理解AI模型分类与汇总
人工智能领域视频模型大体也经历了从传统手工特征,到卷积神经网络、双流网络(2014年-2017年)、3D卷积网络、transformer的发展脉络。为了时序信息,有的模型也结合用LSTM。 视频的技术大多借鉴图像处理技术,只是视频比…...
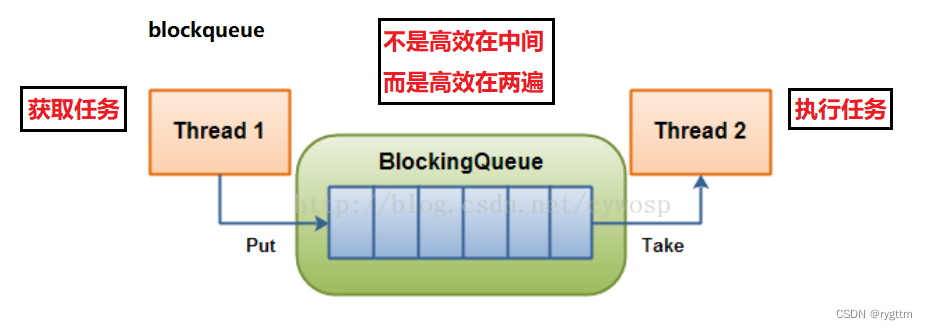
【Linux】多线程 --- 线程同步与互斥+生产消费模型
人生总是那么痛苦吗?还是只有小时候是这样? —总是如此 文章目录 一、线程互斥1.多线程共享资源访问的不安全问题2.提出解决方案:加锁(局部和静态锁的两种初始化/销毁方案)2.1 对于锁的初步理解和实现2.2 局部和全局锁…...

17.模型的定义
学习要点: 1.默认设置 2.模型定义 本节课我们来开始学习数据库的模型部分的定义和默认值的设置。 一.默认设置 1. 框架可以使用 Eloquent ORM 进行数据库交互,也就是关系对象模型; 2. 在数据库入门阶段,我们已经创建了…...

golang 记录交叉编译sqlite的报错信息 go build -ldflags
go build -ldflags ‘-s -w --extldflags “-static -fpic”’ -o go-web main.go [gos20230512]# CGO_ENABLED1 CCaarch64-linux-gnu-gcc CXXaarch64-linux-gnu-g GOOSlinux GOARCHarm64 go build -ldflags -s -w --extldflags "-static -fpic" -o go-web m…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
