Codeforces Round #699 (Div. 2)
E.

题意:n本书,每本书有颜色a[i],一次操作可以将其中一本书放在末尾,求满足:相同颜色的书都是相邻的 的最小操作次数.
显然最多只需要n次,考虑能节省多少次.倒着考虑,记f[i]为i~n最多能节约的次数.先预处理出每种颜色的出现的位置范围l[i],r[i].
1.不节约这本书f[i] = f[i + 1]
2.if i == l[a[i]], f[i] = cnt[a[i]] + f[r[a[i]]+1]
3.if i != l[a[i]], f[i] = cnt[a[i]](位置i后的a[i]个数),为什么不加上f[r[a[i]]+1]呢?首先这个转移必然不可能是最优的,肯定会被前面i = l[a[i]]时替换掉,所以我们只考虑这部分被继承时的情况.如果被继承只有可能前面出现i' == l[a[i']],并且r[a[i']]>i,那么f[i'] = cnt[a[i']] + f[r[a[i']+1]],此时我们保留a[i']和i以及i后面的a[i]不动,先将i前面i'后面的a[i]移到末尾,再把其他与a[i],a[i']不同的数移到末尾即可.
#include <bits/stdc++.h>
#define int long long
#define IOS ios::sync_with_stdio(false), cin.tie(0)
#define ll long long
// #define double long double
#define ull unsigned long long
#define PII pair<int, int>
#define PDI pair<double, int>
#define PDD pair<double, double>
#define debug(a) cout << #a << " = " << a << endl
#define point(n) cout << fixed << setprecision(n)
#define all(x) (x).begin(), (x).end()
#define mem(x, y) memset((x), (y), sizeof(x))
#define lbt(x) (x & (-x))
#define SZ(x) ((x).size())
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
// namespace nqio { const unsigned R = 4e5, W = 4e5; char* a, * b, i[R], o[W], * c = o, * d = o + W, h[40], * p = h, y; bool s; struct q { void r(char& x) { x = a == b && (b = (a = i) + fread(i, 1, R, stdin), a == b) ? -1 : *a++; } void f() { fwrite(o, 1, c - o, stdout); c = o; } ~q() { f(); }void w(char x) { *c = x; if (++c == d) f(); } q& operator >>(char& x) { do r(x); while (x <= 32); return *this; } q& operator >>(char* x) { do r(*x); while (*x <= 32); while (*x > 32) r(*++x); *x = 0; return *this; } template<typename t> q& operator>>(t& x) { for (r(y), s = 0; !isdigit(y); r(y)) s |= y == 45; if (s) for (x = 0; isdigit(y); r(y)) x = x * 10 - (y ^ 48); else for (x = 0; isdigit(y); r(y)) x = x * 10 + (y ^ 48); return *this; } q& operator <<(char x) { w(x); return *this; }q& operator<< (char* x) { while (*x) w(*x++); return *this; }q& operator <<(const char* x) { while (*x) w(*x++); return *this; }template<typename t> q& operator<< (t x) { if (!x) w(48); else if (x < 0) for (w(45); x; x /= 10) *p++ = 48 | -(x % 10); else for (; x; x /= 10) *p++ = 48 | x % 10; while (p != h) w(*--p); return *this; } }qio; }using nqio::qio;
using namespace std;
mt19937 rnd(random_device{}());
const int N = 2e6 + 10;
int n, a[N], f[N], l[N], r[N];
map<int, int> cnt;
signed main() {IOS;cin >> n;for (int i = 1; i <= n; ++i) {cin >> a[i];}for (int i = 1; i <= n; ++i) {r[a[i]] = i;}for (int i = n; i >= 1; --i) {l[a[i]] = i;}for (int i = n; i >= 1; --i) {++cnt[a[i]];f[i] = f[i + 1];if (i == l[a[i]]) f[i] = max(f[i], f[r[a[i]] + 1] + cnt[a[i]]);else f[i] = max(f[i], cnt[a[i]]);}cout << n - f[1] << "\n";
}F.

题意:对n个节点1为根的树ab染色,有x个a,n-x个b.定义i节点上的字符串为1到i路径上的字符.求字符串种类数最少多少种,输出染色方案.
首先每一层尽可能染成一种颜色,如果恰好平分,那么答案为树的最大深度.这毫无疑问是答案下界,我们再去找答案上界,猜测是最大深度+1.假设我们在染色某一层时,剩下m个点未染色,有t个非叶节点,那么我们肯定能将这t个非叶节点染成同一种颜色,因为至少还有t个叶子节点,我们只需要拿数量多的颜色来染即可,然后染叶子节点,显然能调整成与刚才非叶节点同一种颜色.
问题转化成了将每一层都染成a或者b,能否刚好染好每一层.这是一个典型的多重背包,我们将每层点的个数看成是物品,x或者n - x看成容积,然后求出选出若干层能否得到容积即可.由于要回溯,我们不压缩状态.设f[i][j]为考虑前i个物品,选的点数为j的可行性,可行性多重背包可以用贪心优化成O(nm).修改状态为f[i][j]为前i个物品凑出j的前提下,前i - 1个物品最多凑的价值.
这里详细说一下多重背包的优化方法:
由于我们只关注可行性,所以我们只需要关注会传递可行性的转移即可.
1.如果前i - 1个物品能凑出j,那么显然前i个也肯定能凑出来.if (f[i - 1][j] != -1) f[i][j] = j
2.如果前i - 1个物品凑不出来j,需要用第i个物品配合前i - 1个物品来凑,我们让体积从小到大枚举,先得到小于j能凑出来的体积,如果能凑出j - v[i],(v[i]为第i个物品的体积),那么如果还有至少一个i号物品,肯定能凑出j - v[i],换而言之,如果f[j - v[i]] != -1 && (j - f[i][j - v[i]) / v[i] <= cnt[i],那么f[i][j] = f[i][j - v[i]].
回溯的时候,我们需要求出拼成容积m每个价值的物品用了多少个.可以倒着来used[i] = (cur - f[i][cur]) / v[i]; cur = f[i][cur].
#include <bits/stdc++.h>
#define int long long
#define IOS ios::sync_with_stdio(false), cin.tie(0)
#define ll long long
// #define double long double
#define ull unsigned long long
#define PII pair<int, int>
#define PDI pair<double, int>
#define PDD pair<double, double>
#define debug(a) cout << #a << " = " << a << endl
#define point(n) cout << fixed << setprecision(n)
#define all(x) (x).begin(), (x).end()
#define mem(x, y) memset((x), (y), sizeof(x))
#define lbt(x) (x & (-x))
#define SZ(x) ((x).size())
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
// namespace nqio { const unsigned R = 4e5, W = 4e5; char* a, * b, i[R], o[W], * c = o, * d = o + W, h[40], * p = h, y; bool s; struct q { void r(char& x) { x = a == b && (b = (a = i) + fread(i, 1, R, stdin), a == b) ? -1 : *a++; } void f() { fwrite(o, 1, c - o, stdout); c = o; } ~q() { f(); }void w(char x) { *c = x; if (++c == d) f(); } q& operator >>(char& x) { do r(x); while (x <= 32); return *this; } q& operator >>(char* x) { do r(*x); while (*x <= 32); while (*x > 32) r(*++x); *x = 0; return *this; } template<typename t> q& operator>>(t& x) { for (r(y), s = 0; !isdigit(y); r(y)) s |= y == 45; if (s) for (x = 0; isdigit(y); r(y)) x = x * 10 - (y ^ 48); else for (x = 0; isdigit(y); r(y)) x = x * 10 + (y ^ 48); return *this; } q& operator <<(char x) { w(x); return *this; }q& operator<< (char* x) { while (*x) w(*x++); return *this; }q& operator <<(const char* x) { while (*x) w(*x++); return *this; }template<typename t> q& operator<< (t x) { if (!x) w(48); else if (x < 0) for (w(45); x; x /= 10) *p++ = 48 | -(x % 10); else for (; x; x /= 10) *p++ = 48 | x % 10; while (p != h) w(*--p); return *this; } }qio; }using nqio::qio;
using namespace std;
mt19937 rnd(random_device{}());
const int N = 2e6 + 10;
int n, a[N], f[N], l[N], r[N];
map<int, int> cnt;
signed main() {IOS;cin >> n;for (int i = 1; i <= n; ++i) {cin >> a[i];}for (int i = 1; i <= n; ++i) {r[a[i]] = i;}for (int i = n; i >= 1; --i) {l[a[i]] = i;}for (int i = n; i >= 1; --i) {++cnt[a[i]];f[i] = f[i + 1];if (i == l[a[i]]) f[i] = max(f[i], f[r[a[i]] + 1] + cnt[a[i]]);else f[i] = max(f[i], cnt[a[i]]);}cout << n - f[1] << "\n";
}相关文章:

Codeforces Round #699 (Div. 2)
E. 题意:n本书,每本书有颜色a[i],一次操作可以将其中一本书放在末尾,求满足:相同颜色的书都是相邻的 的最小操作次数. 显然最多只需要n次,考虑能节省多少次.倒着考虑,记f[i]为i~n最多能节约的次数.先预处理出每种颜色的出现的位置范围l[i],r[i]. 1.不节约这本书f[i] f[i 1]…...

MySQL存储过程的传参和流程控制
目录 一.存储过程传参—in 演示 二.存储过程传参—out 演示 三.存储过程传参—inout 演示 四.流程控制—判断 格式 演示 五.流程控制—case 语法 演示 六.流程控制—循环 循环—while 循环—repeat 循环—loop 一.存储过程传参—in in表示传入的参数,可以传…...
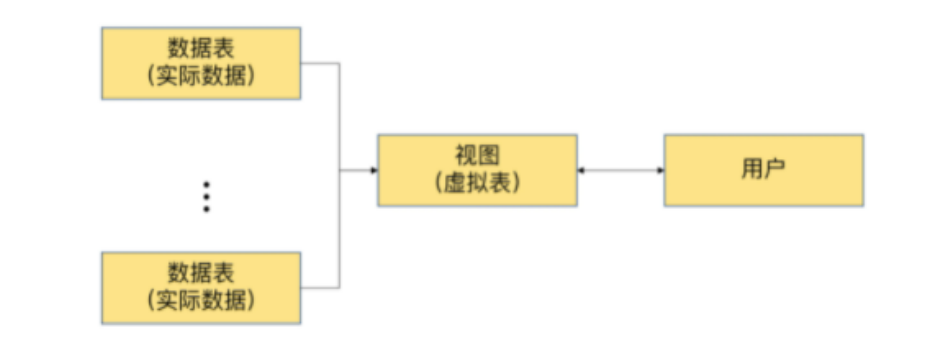
MySQl学习(从入门到精通11)
MySQl学习(从入门到精通11)第 14 章_视图1. 常见的数据库对象2. 视图概述2. 1 为什么使用视图?2. 2 视图的理解3. 创建视图3. 1 创建单表视图3. 2 创建多表联合视图3. 3 基于视图创建视图4. 查看视图5. 更新视图的数据5. 1 一般情况5. 2 不可…...

关于ThreadLocal
弱引用 1.1 java中的各种引用和测试: https://blog.csdn.net/thewindkee/article/details/102723838 1.2 treadlocal中的弱引用测试: https://blog.csdn.net/thewindkee/article/details/103726942 (这篇很重要) 内存泄露: https://zhuanlan.zhihu.com/p/523628871 综合考虑 …...

【C++】类和对象(中)
文章目录1. 类的6个默认成员函数2. 构造函数概念特性3. 析构函数概念特性4. 拷贝构造函数概念特征5. 运算符重载5.1 前置和后置重载5.2 赋值运算符重载6. 日期类的实现7. const成员8. 取地址及const取地址操作符重载1. 类的6个默认成员函数 如果一个类中什么成员都没有&#x…...

js下载文件
url为文件的src地址 url必须符合同源策略或者url的接口地址允许跨域,否则浏览器会报跨域错误 axios.get(data.url ,{ responseType: ‘blob’, }) .then( response>{ let blob new Blob([response.data]); let url window.URL.createObjectURL(blob); // 创建 …...

ESP8266 + STC15+ I2C OLED带网络校时功能的定时器时钟
ESP8266 + STC15+ I2C OLED带网络校时功能的定时器时钟 📍相关篇《ESP8266 + STC15基于AT指令通过TCP通讯协议获取时间》 📌ESP8266 AT固件基于安信可AT固件,相关刷AT固件可以参考《NodeMCU-刷写AT固件》 🔖STC15 单片机采用的是:STC15F2K60S2 晶振频率采用内部:22.11…...

计算机入门基础知识大全
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的,绽…...

Python程序出现错误怎么办?
Python 异常处理 python提供了两个非常重要的功能来处理python程序在运行中出现的异常和错误。你可以使用该功能来调试python程序。 异常处理: 本站Python教程会具体介绍。 断言(Assertions):本站Python教程会具体介绍。 python标准异常 异常名称 描述 BaseException 所有异常…...

【Vue3】v-if和v-for优先级
🎈博客主页:🌈我的主页🌈 🎈欢迎点赞 👍 收藏 🌟留言 📝 欢迎讨论!👏 🎈本文由 【泠青沼~】 原创,首发于 CSDN🚩…...

Windows上实现 IOS 自动化测试
本文介绍如何使用tideviceWDAairtest/facebook-wda实现在Windows上进行IOS APP自动化测试 环境准备 Windows Python环境 Python 3.6 WebDriverAgent安装 下载最新的项目到Mac:https://github.com/appium/WebDriverAgent $ git clone https://github.com/appiu…...
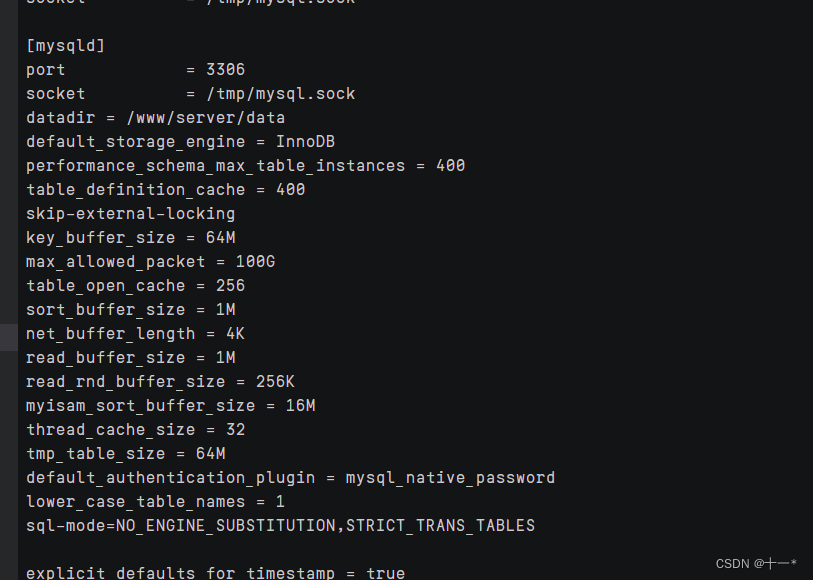
Linux云服务器下怎么重置MySQL8.0数据库密码
文章目录一、修改my.cnf配置文件为mysql免登陆二、免密登陆mysql三.给root用户重置密码1、首先查看当前root用户相关信息,在mysql数据库的user表中2、把root密码置为空3、退出mysql,删除/etc/my.cnf文件中添加进去的skip-grant-tables 重启mysql服务4、使…...
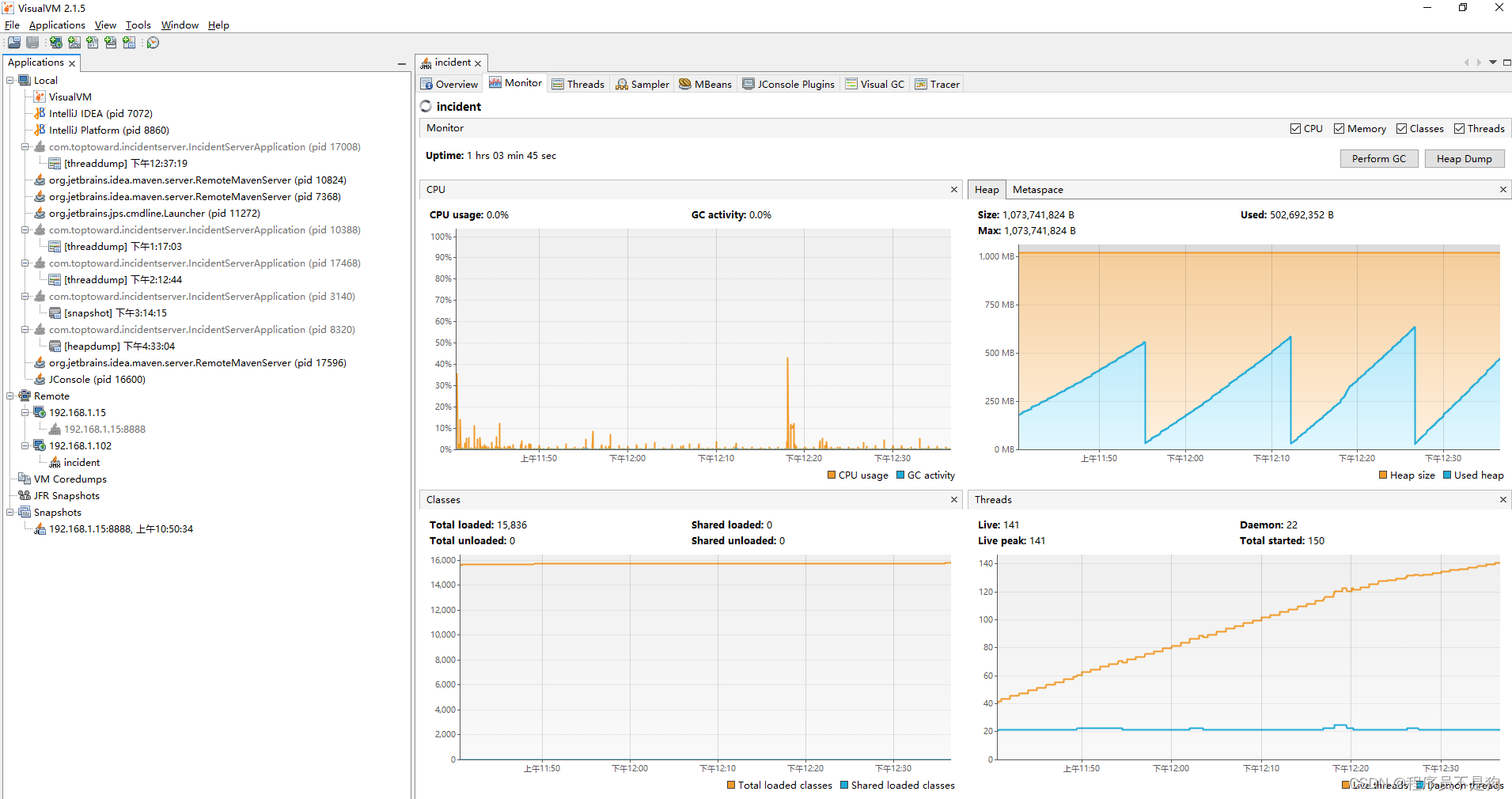
JVM调优
JVM调优-VisualVmVisualVm/ Jconsule远程连接第一种方式第二种方式:java 11开启远程GC连接如果还连不上考虑防火墙拦截了端口firewall-cmd --list-all,查看一下并暴露对应端口连接配置VisualVm界面简介采集GC信息的一些命令垃圾回收器切换VisualVm/ Jconsule远程连接…...
【配电网规划】SOCPR和基于线性离散最优潮流(OPF)模型的配电网规划( DNP )(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

锦正茂EM3电磁铁的技术参数
产品特点: ※U形结构、视野开阔、磁场强度高、磁场强度大小调节方便 ※体积小、重量轻、占空比小、结构紧凑、磁场性能更佳 ※电磁铁的工作气隙调节轻便灵活,极头处设有螺纹,更换极头装卸方便 ※可选配工作间隙刻度指示 ※小气隙时用于铁…...

Go最新版下载 Go1.20版新特性
Go官方正式发布了Go1.20稳定版 该版本依然保持 Go1 兼容性,可以升级到 Go1.20,而不需要做任何代码改动。 可以使用你任何喜欢的方式升级: 比如: go install golang.org/dl/go1.20latest 具体的可以参考官网教程: ht…...

Pywirt:一款基于Python的Windows安全应急响应工具
关于Pywirt Pywirt是一款基于Python开发的网络安全工具,该工具专门针对Windows操作系统设计,可以帮助广大研究人员使用winrm并通过在Windows操作系统上收集各种信息来加快安全事件应急响应的速度。 该工具已在Windows 10操作系统上进行过完整测试。 功…...

KDZD832 智能蓄电池活化仪
一、产品概述 KDZD832 智能蓄电池活化仪(2V-24V 一体机,适用于 2V、6V、12V/24V 蓄电池,以下简称活化仪),是专用于日常维护中对落后蓄电池处理的便携式产品,它具有四种独立的使用方式:电池放电…...

纯css实现loading加载中(多种展现形式)
前言 现如今网页越来越趋近于动画,相信大家平时浏览网页或多或少都能看到一些动画效果,今天我们来做一个有意思的动画效果,纯 css 实现 loading 加载中(多种展现形式),下面一起看看吧。 1. 常规 loading 实…...

【面试题】2023 vue高频面试知识点汇总
一、MVVM原理在Vue2官方文档中没有找到Vue是MVVM的直接证据,但文档有提到:虽然没有完全遵循MVVM模型,但是 Vue 的设计也受到了它的启发,因此在文档中经常会使用vm(ViewModel 的缩写) 这个变量名表示 Vue 实例。为了感受MVVM模型的…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

【2D与3D SLAM中的扫描匹配算法全面解析】
引言 扫描匹配(Scan Matching)是同步定位与地图构建(SLAM)系统中的核心组件,它通过对齐连续的传感器观测数据来估计机器人的运动。本文将深入探讨2D和3D SLAM中的各种扫描匹配算法,包括数学原理、实现细节以及实际应用中的性能对比,特别关注…...
