承诺协议:定义 构造
文章目录
- 安全性定义
- 方案构造
- 基于 OWP 存在性
- 基于 DL 假设
- 基于 OWF 存在性
- 基于 DDH 假设
- 总结
安全性定义
承诺协议(Commitment Scheme)是一个两阶段的两方协议。一方是承诺者(Committer) C C C,另一方是接收者(Receiver) R R R,两者都是 PPT 能力的。形式化描述如下:

承诺协议的安全性分为两部分:绑定性(Binding)、隐藏性(Hiding)。Binding 是用于保护 R R R 的,使得恶意的 C C C 无法将已有的承诺值 Open 成不同的内容。Hiding 是用于保护 C C C 的,使得恶意的 R R R 无法从承诺值中获得有关于内容的信息。

如果考虑 unbounded 敌手,那么可以得到 Perfect、Statistical、Computational 三种安全强度。
- Perfect Binding 是说:每一个承诺值 c c c,都仅存在一个 ( m , d e c ) (m,dec) (m,dec) 与之对应,从而无界敌手也不能找出一对不同的消息。在 Statistical 版本中,存在多个消息与之对应的承诺值的占比(依赖于 R R R 的随机带)可忽略。
- Perfect Hiding 是说:任意的两个消息 m 0 ≠ m 1 m_0 \neq m_1 m0=m1,它们的承诺值 c c c 的分布(依赖于 C C C 的随机带)完全相同。在 Statistical 版本中,两者的统计距离可忽略。
Perfect / Statistical Binding 与 Perfect / Statistical Hiding 不可同时存在:
- 如果是 Statistical Binding 的,那么承诺值 c c c 几乎总是仅能对应两个消息 m 0 ≠ m 1 m_0 \neq m_1 m0=m1 的其中之一,无界敌手总可以穷举所有的随机带找出这个 m b m_b mb,从而打破 Hiding(不是 Statistical Hiding)
- 如果是 Statistical Hiding 的,那么承诺值 c c c 几乎总是可以对应两个消息 m 0 ≠ m 1 m_0 \neq m_1 m0=m1,无界敌手总可以穷举所有的随机带找出对应的 d e c 0 , d e c 1 dec_0,dec_1 dec0,dec1,从而打破 Binding(不是 Statistical Binding)
- Perfect 导致 Statistical,因此 Perfect 也无法共存
在 PZK IP 中,有 “实例依赖” 的承诺方案:对于 x ∈ L x \in L x∈L 可以达成 Perfect Hiding(从而是 Perfect ZK),对于 x ∉ L x \notin L x∈/L 可以达成 Perfect Binding(从而是 Proof System)。
方案构造
承诺方案的存在性,等价于 ZKP 的存在性。在标准假设下,承诺方案存在,于是 ZKP 也存在。下面给出若干种构造。
基于 OWP 存在性
假设 OWP f ′ ( x ) f'(x) f′(x) 存在,那么可以利用 Goldreich-Levin 定理,给出一个带有 hardcore h ( x , r ) = ⟨ x , r ⟩ h(x,r)=\langle x,r \rangle h(x,r)=⟨x,r⟩ 的新 OWP f ( x , r ) = ( f ′ ( x ) , r ) f(x,r)=(f'(x),r) f(x,r)=(f′(x),r)
基于 OWP 的比特承诺方案:

它是 Perfect-Binding and Computational-Hiding 的非交互承诺协议。因为 OWP 是置换,因此它完美绑定了随机数。其隐藏性来源于 OWP 的单向性。
基于 DL 假设
如果素数 p p p 满足 p − 1 = ∏ i q i p-1=\prod_iq_i p−1=∏iqi 可分解为若干小的素因子 q i q_i qi,那么基于 CRT 分解,可以快速穷举出每个子群 G q i ⊆ Z p ∗ G_{q_i} \subseteq \mathbb Z_p^* Gqi⊆Zp∗ 上的 DL 问题的解。从而在这种素数下, Z p ∗ \mathbb Z_p^* Zp∗ 上的 DL 问题不难。
如果素数 p = 2 q + 1 p=2q+1 p=2q+1,其中 q q q 是大素数,此时上述的攻击方法就必须爆破阶 q q q 的子群 G q ⊆ Z p ∗ G_{q} \subseteq \mathbb Z_p^* Gq⊆Zp∗ 上的 DL 问题。然而,根据 x x x 的奇偶性 ( g x ) ( p − 1 ) / 2 (g^x)^{(p-1)/2} (gx)(p−1)/2 分别等于 + 1 , − 1 +1,-1 +1,−1,由于 ( g x , g y , g x y ) (g^x,g^y,g^{xy}) (gx,gy,gxy) 指数的奇偶性有关系,因此可以快速与 ( g x , g y , g z ) (g^x,g^y,g^z) (gx,gy,gz) 做区分。从而在这种素数下, Z p ∗ \mathbb Z_p^* Zp∗ 上的 DDH 问题不难。
如果我们选取形如 p = 2 q + 1 p=2q+1 p=2q+1 的大素数,在循环群 Z p ∗ = < g > \mathbb Z_p^* = <g> Zp∗=<g> 中选择二次剩余群 Q R ( p ) = < g 2 > QR(p)=<g^2> QR(p)=<g2> 作为 DDH 问题的群,那么就使得所有群元素的指数都是偶数,从而避免上述的奇偶分析。假设这种群上的 DDH 问题是困难的,因为在 Cook 归约下 D D H ≤ c C D H ≤ c D L DDH \le_c CDH \le_c DL DDH≤cCDH≤cDL,因此在 Q R ( 2 q + 1 ) QR(2q+1) QR(2q+1) 上的 DL 问题也是困难的。
基于离散对数问题的 Pedersen 承诺方案(关于群元素的,而非单比特):

它是 Computational-Binding and Perfect-Hiding 的2-round承诺协议。假如 r r r 均匀采样那么 h r h^r hr 也是均匀的,因此是完美隐藏的。其绑定性来源于 h = g x h=g^x h=gx 的 DL 问题。
可以证明,对于 non-uniform 敌手 C ∗ C^* C∗,不存在非交互 Perfect-Hiding 的承诺协议可以达成 Binding 安全性。因为是 Perfect Hidng,因此承诺值 c c c 可以对应两个不同的消息 ( m 0 , r 0 ) , ( m 1 , r 1 ) (m_0,r_0),(m_1,r_1) (m0,r0),(m1,r1),因此可以把它作为 advice 写入到某个 non-uniform PPT 敌手 C ∗ C^* C∗(存在性),这就打破了 Computational Binding(因此必须引入 R R R 的随机性,这需要交互)
不过,确实存在基于 hash 的非交互 statistical-hiding and computational-binding 的承诺协议,可以抵御 uniform(能力弱)PPT 的敌手 C ∗ C^* C∗ [Halevi, Micali, 96]
基于 OWF 存在性
OWP 存在性的假设较强,实际上只要 OWF 存在就可以导致承诺协议存在。密码学课程都会讲授 Levin 的从带 hardcore OWP 构造 PRG 的方法,而 [Hill90] 证明了 OWF 就可以构造出 PRG(但是很复杂)。
基于 OWF 的 Naor 比特承诺方案:

它是 Statistical-Binding and Computational-Hiding 的2-round承诺协议。由于 G G G 将 n n n 比特的 r r r 拉长为 3 n 3n 3n 比特,因此 G ( r 0 ) ⊕ G ( r 1 ) G(r_0) \oplus G(r_1) G(r0)⊕G(r1) 仅仅有 2 2 n 2^{2n} 22n 种取值,但是 x ∈ { 0 , 1 } 3 n x \in \{0,1\}^{3n} x∈{0,1}3n 有 2 3 n 2^{3n} 23n 种取值,仅仅占比 n e g l ( n ) negl(n) negl(n) 的随机串可能被敌手利用,然而 x x x 是被诚实的 R R R 均匀掷出的。其隐藏性来源于 PRG 的伪随机性。
那么,是否可以基于 OWF 构造 Statistical-Hiding 的承诺方案呢?假如 hiding 仅仅来源于 one-way,那么无界敌手 C ∗ C^* C∗ 必然可以求逆,从而打破它。令人吃惊的是,[Haitner, Nguyen, et al. 09] 给出了一种构造。
基于 DDH 假设
基于 OWP 的 Perfect-Binding 比特承诺方案,当遇到了需要承诺多个比特的情况时,就必须独立执行多次。如果串行组合,根据 Sequential composition theorems 这依然是安全的,但是 round complexity 就会快速上升;如果并行组合,那么这就很复杂了(基于游戏的归约,loss factor 可能会是指数级;基于模拟的归约,rewind 次数可能会是指数级)。
基于 DDH 问题的 ElGamal 承诺协议(关于群元素的,而非单比特):

它是 Perfect-Binding and Computational-Hiding 的非交互承诺协议。因为 g r g^r gr 是置换,因此这是完美绑定的。可以将 DDH 问题归约到打破它的隐藏性:输入一个三元组 ( g x , g y , g z ) (g^x,g^y,g^z) (gx,gy,gz),将 h h h 替换为 g x g^x gx,将 g r g^r gr 替换为 g y g^y gy,因为它们都是均匀分布。接着将 g m b h r g^{m_b}h^r gmbhr 替换为 g m b g z g^{m_b}g^z gmbgz:假如 z z z 均匀,那么 g m 0 g z g^{m_0}g^z gm0gz 和 g m 1 g z g^{m_1}g^z gm1gz 同分布,无界敌手也不能给出有偏的输出分布;假如 z = x y z=xy z=xy,那么 g m b g z g^{m_b}g^z gmbgz 和 g m b h r g^{m_b}h^r gmbhr 同分布,于是针对 Hiding 的敌手 ( R ∗ , D ) (R^*,D) (R∗,D) 就转化为了针对 DDH 的敌手。
总结
下面的 Round Complexity 考虑的是 Committing 阶段的,而 Opening 阶段直接发送 C C C 所使用的随机带即可(必然是 1-round 的)。
- 如果 DL 假设成立,则存在 2-round 的 perfect-hiding 以及 computational-binding 的承诺协议(二次剩余群上的 Pedersen 承诺方案)
- 如果 OWF 存在,则存在 2-round 的 computational-hiding 以及 statistical-binding 的承诺协议(基于 PRG 的 Naor’s 比特承诺方案)
- 如果 OWP 存在,则存在 1-round 的 computational-hiding 以及 perfect-binding 的承诺协议(基于 hardcore 的比特承诺方案)
- 如果 DDH 假设成立,则存在 1-round 的 computational-hiding 以及 perfect-binding 的承诺协议(二次剩余群上的 ElGamal 承诺方案)
前三者可以被用于 Blum’s ZKP for HC 的构造,从而导出 ZKP 的存在性结论。
相关文章:

承诺协议:定义 构造
文章目录 安全性定义方案构造基于 OWP 存在性基于 DL 假设基于 OWF 存在性基于 DDH 假设 总结 安全性定义 承诺协议(Commitment Scheme)是一个两阶段的两方协议。一方是承诺者(Committer) C C C,另一方是接收者&#…...

二、easyUI中的layout(布局)组件
1.layout(布局)组件的概述 布局容器有5个区域:北、南、东、西和中间。中间区域面板是必须的,边缘的面板都是可选的。每个边缘区域面板都可以通过拖拽其边框改变大小,也可以点击折叠按钮将面板折叠起来。布局可以进行嵌…...

MySQL---聚合函数、字符串函数、数学函数、日期函数
1. 聚合函数 数据准备: create database mydb4; use mydb4;create table emp(emp_id int primary key auto_increment comment 编号,emp_name char(20) not null default comment 姓名,salary decimal(10,2) not null default 0 comment 工资,department char(20…...

边缘计算盒子有哪些?边缘计算应用场景
边缘计算(Edge Computing)是一种分布式计算模型,旨在将数据处理和计算功能从中心数据中心移到数据源附近的边缘设备上。它的目标是在接近数据生成的地方进行实时数据处理和分析,减少数据传输延迟和网络拥塞,提高应用程…...
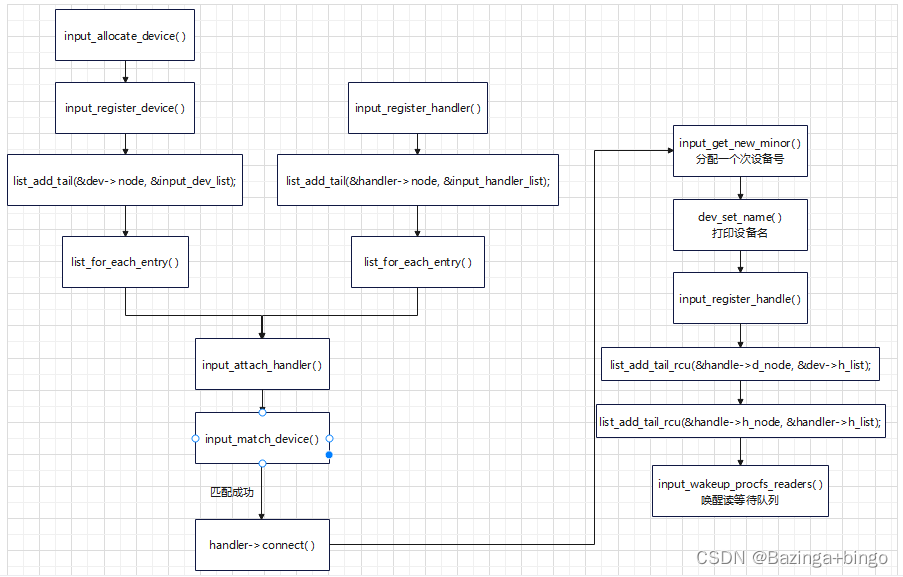
Linux内核(十四)Input 子系统详解 IV —— 配对的input设备与input事件处理器 input_register_handle
文章目录 input_handle结构体详解配对的input设备与input事件处理器实例input核心层对驱动层和事件层之间的框架建立流程图 本文章中与input子系统相关的结构体可参考input子系统结构体解析 input函数路径:drivers/input/input.c input_handle结构体详解 input_ha…...
)
Vue2.x源码解析(三)
Platform 函数 Platform 函数是用于与各种浏览器和平台进行交互的函数,它为 Vue 提供了跨平台的支持,例如浏览器、Node.js 等。Platform 函数提供了一些常用的工具和配置项,例如事件的托管、资源请求和异步更新等。下面是 Platform 函数的伪…...
)
全面理解守护进程的基础概念,以及如何创建一个守护进程(系列文章第三篇)
前言 这个系列的文章有四篇,其目的是为了搞清楚: 进程,shell,shell进程,终端,控制终端,前台进程,后台进程,控制进程,前台进程组,后台进程组&#…...

Leetcode刷题日志5.0
目录 前言: 1.两数相加 2.无重复字符的最长子串 3.整数反转 4.删除链表的倒数第 N 个结点 前言: 今天我又来继续分享最近做的题了,现在开始进入我们快乐的刷题时间吧!(编程语言Python3.0,难度…...

母亲节:向世界上最伟大的母爱致敬
在这世间众多的亲情关系中,有一种关系无与伦比,毫不费力地凌驾于其他任何已知的地球关系之上。这种非凡的关系就是母亲与子女之间的关系。 母亲对家庭无尽的爱、奉献和忠诚使这份感情无价。为了向全球所有母亲表示敬意,母亲节在世界46个国家庆…...
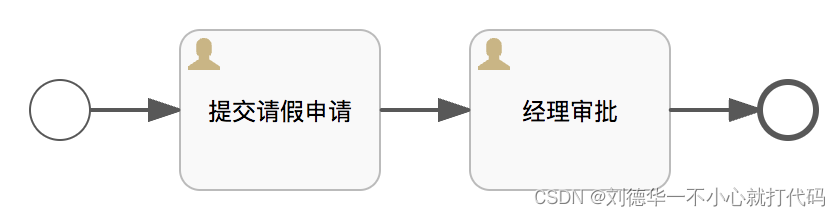
Springboot +Flowable,各种历史信息如何查询(二)
一.简介 正在执行的流程信息是保存在以 ACT_RU_ 为前缀的表中,执行完毕的流程信息则保存在以 ACT_HI_ 为前缀的表中,也就是流程历史信息表。 假设有一个流程,流程图如下: 当这个流程执行完毕后,以 ACT_RU_ 为前缀的…...

DataX下载安装使用
文章目录 01.Clickhouse到HBase(Phoenix)数据导入 DataX介绍下载执行同步的组件配置数据同步查看官方读写配置样例创建Hbase和Phoenix表创建ClickHouse表写入ClickHouse测试数据编写ClickHouse2Hbase配置文件执行同步命令 拓展ClickHouse同步到MySQL配置文件 01.Clickhouse到HB…...
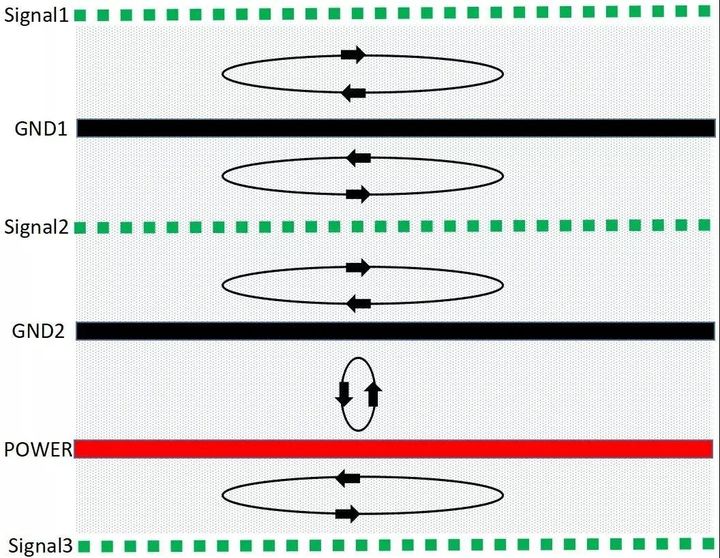
PCB多层板 : 磁通对消法有效控制EMC
在PCB的EMC设计考虑中,首先涉及的便是层的设置;单板的层数由电源、地的层数和信号层数组成;在产品的EMC设计中,除了元器件的选择和电路设计之外,良好的PCB设计也是一个非常重要的因素。 PCB的EMC设计的关键࿰…...

基于正点原子电机实验的pid调试助手代码解析(速度环控制)
这里写目录标题 下位机与PID调试助手传输的原理代码讲解(基于正点原子)解析数据接受和数据发送的底层函数数据接受数据帧格式环形数组以及怎么找到它的帧头位置crc校验 数据发送数据上传函数 通过前两节文章,我已经了解了基本的pid算法,现在在完成了电机…...
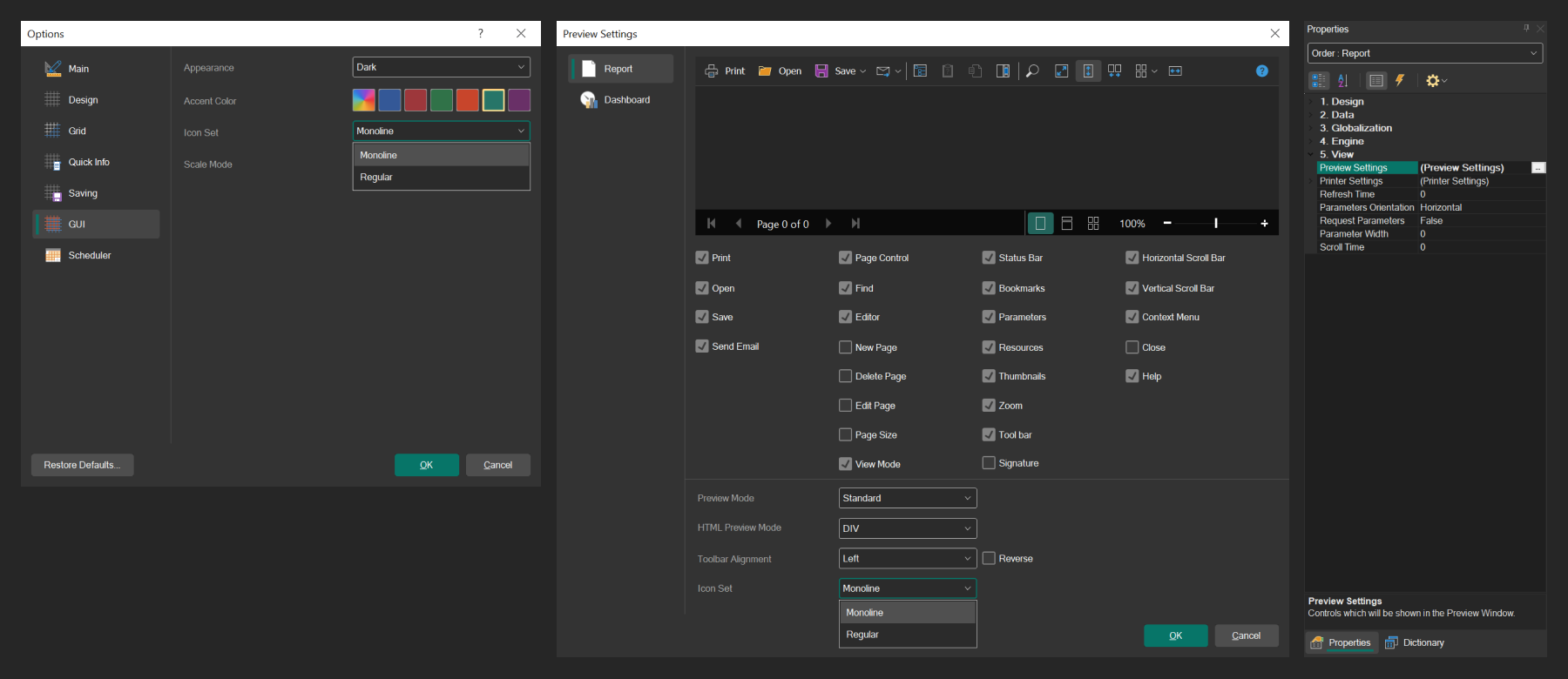
报表设计器Stimulsoft 2023.2提供深色主题和 Monoline 图标包
Stimulsoft Reports 是一款报告编写器,主要用于在桌面和Web上从头开始创建任何复杂的报告。可以在大多数平台上轻松实现部署,如ASP.NET, WinForms, .NET Core, JavaScript, WPF, Angular, Blazor, PHP, Java等,在你的应用程序中嵌入报告设计器…...

文本三剑客之——sed编辑器
sed编辑器 sed编辑器sed基础语法sed查询sed删除sed 替换sed 插入 sed编辑器 sed是文本处理工具,依赖于正则表达式,可以读取文本内容,工具指定条件对数据进行添加、删除、替换等操作,被广泛应用于shell脚本,以完成自动…...

华为OD机试真题 Java 实现【贪心的商人】【2023Q1 100分】
一、题目描述 商人经营一家店铺,有number种商品,由于仓库限制每件商品的最大持有数量是item[index],每种商品的价格在每天是item_price[item_index][day],通过对商品的买进和卖出获取利润,请给出商人在days天内能获取到的最大利润。 注:同一件商品可以反复买进和卖出;…...

《数据结构与算法C++版》实验二-链表实验
一、实验内容 实验目的 1、实现线性表的链式存储结构(链表)。 2、熟悉 C++程序的基本结构,掌握程序中的头文件、实现文件和主文件之间的 相互关系及各自的作用。 3、熟悉链表的基本操作方式,掌握链表相关操作的具体实现。 实验内容 对链式存储结构的线性表进行一些基本操作…...

【2023华为OD笔试必会25题--C语言版】《06 简单的自动曝光》——数组
本专栏收录了华为OD 2022 Q4和2023Q1笔试题目,100分类别中的出现频率最高(至少出现100次)的25道,每篇文章包括原始题目 和 我亲自编写并在Visual Studio中运行成功的C语言代码。 仅供参考、启发使用,切不可照搬、照抄,查重倒是可以过,但后面的技术面试还是会暴露的。✨✨…...
Science Advances:宋艳课题组发现经颅近红外激光刺激可提升人类工作记忆
图1. 新闻稿封面 工作记忆——在几秒钟内主动“记住”有用信息的能力——在许多高级认知活动中起着至关重要的作用。由于工作记忆能力的个体差异可以预测流体智力和广泛的认知功能,这使得提高工作记忆能力成为干预和增强的有吸引力的目标。 美国食品及药品管理局声…...

Linux系统crash后定位方法-PCIE举例
crash解释 在Linux操作系统中,"crash"通常是指一种用于分析系统崩溃(crash)的工具或方法。当系统发生崩溃时,可能会产生一些关键信息,如错误日志、内存转储文件等。使用crash工具可以分析这些信息ÿ…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
