横截面收益率
横截面收益率指的是在经典资产定价模型中,在横截面上线性确定的一个与资产风险匹配的资产收益率。
横截面收益率的预测[1]
(一)变量和方法
我们主要使用月度频率数据进行检验。交易数据和公司财务数据来自于CSMAR数据库。CSMAR数据库的收益率调整了送股、配股以及拆细等公司股本变动,使得前后的收益率具有可比性。样本包含沪深A股的上市股票,剔除了PT,ST的股票。进入样本的股票要求具有当月和之前一个月的月度收益率、换手率以及至少15天的日度换手率数据。样本区间为1995年1月至2010年12月。1995年之前上市的股票较少,且公司法在1994年正式颁布,公司之间的财务数据开始具有可比性。最后共有172792个公司-月度观测值,其中平均每个月有约981个观测值,最少的月份有169个观测值,最多的月份有1660个观测值。
文中使用换手率来定义交易活动。换手率定义为交易量和流通市值的比值。一般来说,如果均值扩大一倍,相应的标准差也会扩大一倍。因此为了避免均值对于二阶距的影响,本文将主要使用变异系数作为股票横截面比较的主要变量,在后面的检验中,我们将分别考虑使用标准差来衡量波动和使用交易金额来代替换手率衡量交易行为进行进一步的稳健性检验。变异系数定义为:
CV(Turnover)=Std(Turnover)/Mean(Turnover)
之前,国内有文献使用过去几年内月度交易行动的标准差作为衡量这一波动的影响,得出的结果并不显著。考虑到国内市场主要为个体投资者,投资周期相对较短,只有几个月的时间,因此很多长期的影响并不显著,因此我们主要使用日度交易量构造的月度波动数据进行检验。每个月,我们使用日度交易数据构造二阶距然后检验对于未来收益率的影响。我们在稳健性检验中使用3个月和6个月的时间跨度构造的变量进行检验,并不影响我们的主要结果。
在检验过程中,我们选取的控制变量包括公司规模,账面市值比,股票动量以及衡量股票流动性的指标和股票个体波动性的指标。主要控制变量的定义在表1中。为避免异常值的影响,利用Winsorize方法对相关变量在1%和99%分位数进行处理。表2是相关变量之间的Pearson相关系数,可以初步看到变量之间的关系。从表中可以看出流通市值小和账面市值比低的公司具有更高的换手率和换手率波动。一般来说大公司能够提供更好的流动性,这点我们可以从非流动性指标和公司市值的相关系数中看到(-0.73),表明在国内市场上换手率并不是流动性的一个很好的指标。而一般来说小公司以及账面市值比低的公司处于增长期,公司基本价值中不确定性较高,关于公司的信息的准确性也相对较低,因此也会导致投资者意见差异更大,波动更为剧烈,会有更高的换手率和波动率。更进一步的,我们看到换手率波动与公司特质性波动之间显著正相关,考虑到特质波动被用来衡量公司个体风险以及不确定性,这也可以部分印证上面关于公司不确定性与换手率波动之间关系的分析。换手率波动与同期的股票收益率之间显著正相关,而与接下来一个月的月度收益率显著负相关,这与换手率波动高代表了股票价格中转售期权的价值高,因此使得股票价值进一步被高估,未来收益率下降的解释相吻合。
相关文章:

横截面收益率
横截面收益率指的是在经典资产定价模型中,在横截面上线性确定的一个与资产风险匹配的资产收益率。 横截面收益率的预测[1] (一)变量和方法 我们主要使用月度频率数据进行检验。交易数据和公司财务数据来自于CSMAR数据库。CSMAR数据库的收益率调整了送股、配股以及拆…...
C++解析JSON JSONCPP库的使用
首先去GitHub下载JSONCPP的源码: JSonCpp的源码 解压后得到:jsoncpp-master 文件夹 需要的是:jsoncpp-master\src\lib_json 目录下的所有文件和 jsoncpp-master\include\json 目录下的所有文件,在MFC工程目录下新建两个文件夹或…...
不会Elasticsearch标准查询语句,如何分析数仓数据?
1 Elasticsearch的查询语句 ES中提供了一种强大的检索数据方式,这种检索方式称之为Query DSL,Query DSL是利用Rest API传递JSON格式的请求体(Request Body)数据与ES进行交互,这种方式的丰富查询语法让ES检索变得更强大,更简洁。 1.1 查询预发 # GET /…...

获得GitHub Copilot并结合VS Code使用
一、什么是GitHub Copilot GitHub Copilot是一种基于AI的代码生成工具。它使用OpenAI的GPT(生成式预训练Transformer)技术来提供建议。它可以根据您正在编写的代码上下文建议代码片段甚至整个函数。 要使用GitHub Copilot,您需要在编辑器中…...
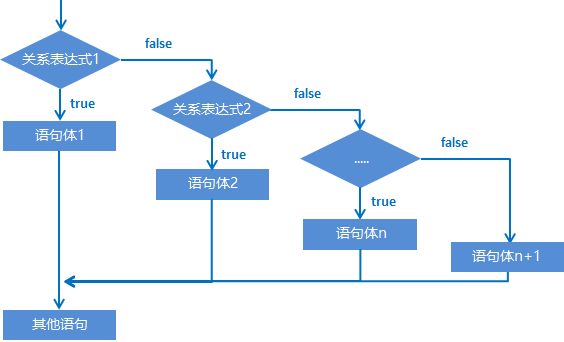
Java基础-判断和循环
1 流程控制语句 在一个程序执行的过程中,各条语句的执行顺序对程序的结果是有直接影响的。所以,我们必须清楚每条语句的执行流程。而且,很多时候要通过控制语句的执行顺序来实现我们想要的功能。 1.1 流程控制语句分类 顺序结构 判…...

ESP32 FreeRTOS学习总结
2023.5.11 FreeRTOS中文数据手册:https://www.freertos.org/zh-cn-cmn-s/RTOS.html 感谢以下两位B站UP主的教程:孤独的二进制、Michael_ee 1.Task 创建任务常用API: 任务函数描述xTaskCreate()使用动态的方法创建一个任务xTaskCreatePinne…...
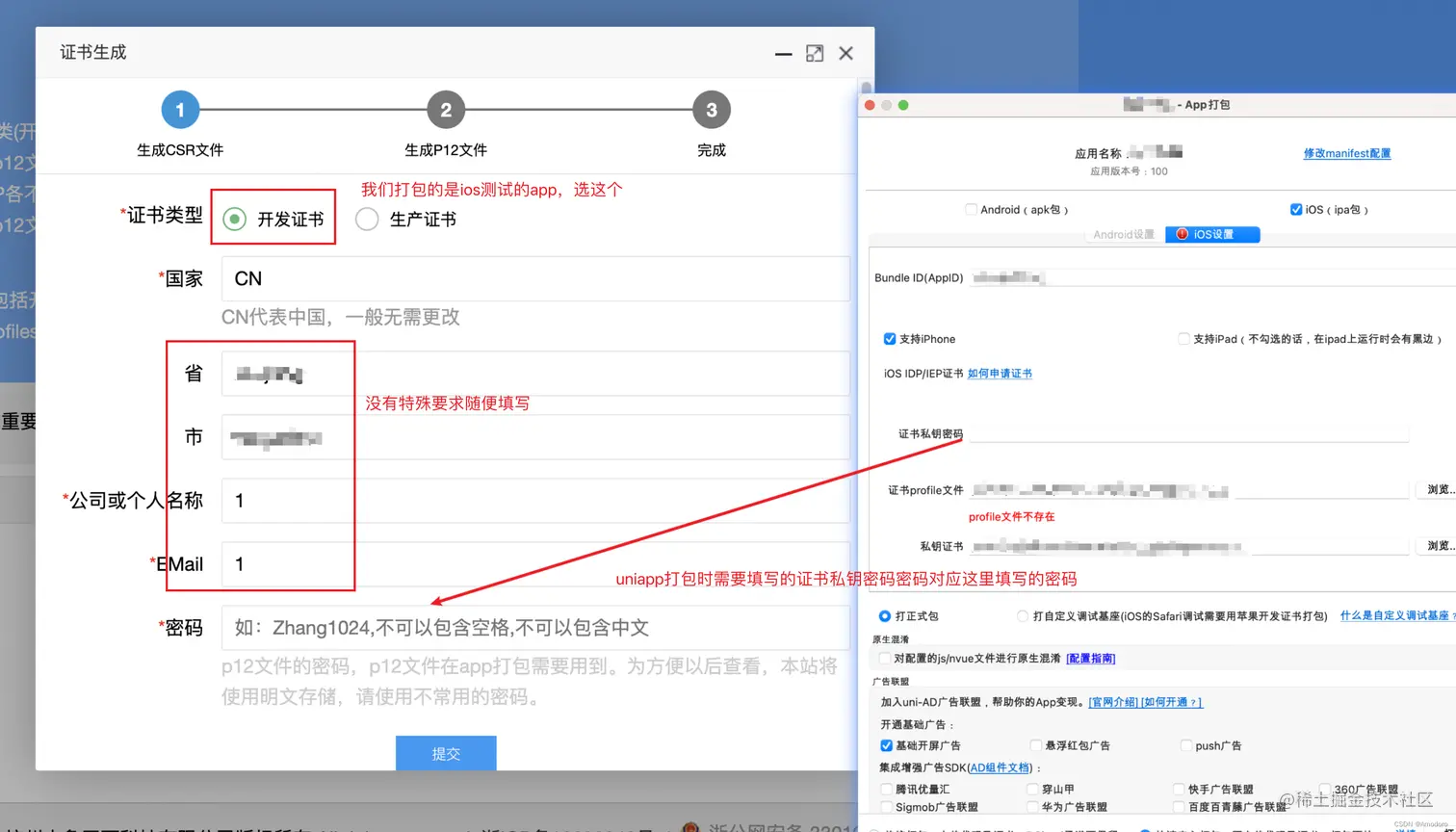
uniapp打包ios保姆式教程【最新】
uniapp打包 打包方式ios打包一、前往官网登录二、添加证书 三、添加标识符(Identifiers)四、添加安装ios测试机(Devices)五、获取证书profile文件六、生成并下载p12文件七、开始打包 打包方式 安卓打包直接使用公共测试证书即可打包成功,简单方便,这里我…...

Thread线程学习(2) Linux线程的创建、终止和回收
目录 1.首先要了解什么是线程ID,以及它的作用是什么 2.创建线程 3.终止线程 4.回收线程 5.总结 在Linux系统中,线程是轻量级的执行单元,能够在同一个进程中并发执行。本文将介绍如何在Linux环境下创建、终止和回收线程,并提供…...

linux-项目部署软件安装
安装jdk 操作步骤: 1、使用FinalShell自带的上传工具将jdk的二进制发布包上传到Linux jdk-8u171-linux-x64.tar.gz 2、解压安装包,命令为tar -zxvf jdk-8u171-linux-x64.tar.gz -C /usr/local 3、配置环境变量,使用vim命令修改/etc/profile文…...
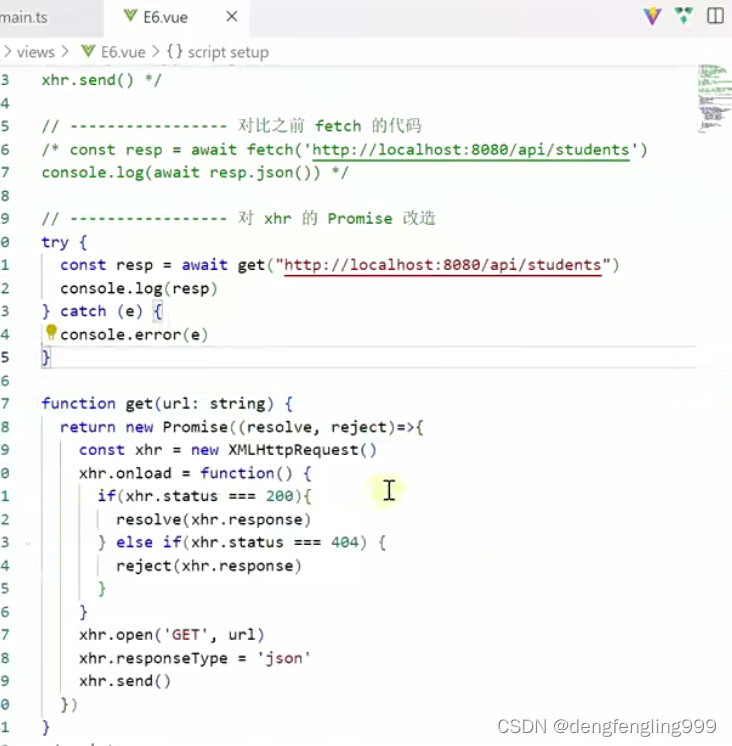
Vue3-黑马(三)
目录: (1)vue3-基础-计算属性 (2) vue3-基础-xhr-基本使用 (3)vue3-基础-xhr-promise改造 (1)vue3-基础-计算属性 上面有重复的代码,用计算属性࿰…...
,sprintf(),snprintf()的函数使用方法(往文件中写入数据,将变量的值转换成字符串输出))
标准C库函数fprintf(),sprintf(),snprintf()的函数使用方法(往文件中写入数据,将变量的值转换成字符串输出)
前言 如果,想要深入的学习标准C库中函数fprintf(),sprintf(),snprintf(),还是需要去自己阅读Linux系统中的帮助文档。 具体输入命令: man 3 fprintf/sprintf/snprintf即可查阅到完整的资料信息。 fprintf 函数 fprin…...

不到1分钟,帮你剪完旅行vlog,火山引擎全新 AI「神器」真的这么绝?
旅行时,想在社交平台发布一支精美的旅行 vlog,拍摄剪辑需要花费多长时间? 20 分钟?一小时?半天? 在火山引擎算法工程师眼里,可能 1 分钟都用不了,因为会有 AI 替你完成。 没错&#…...

MySQL的概念、编译安装,以及自动补全
一.数据库的基本概念 1、数据(Data) • 描述事物的符号记录 • 包括数字,文字,图形,图像,声音,档案记录等 • 以“记录”形式按统一的格式进行存储 2、表 • 将不同的记录组织在一起 • …...

Jmeter常见问题和工作中遇到的问题解决方法汇总
一、标题Jmeter常见问题解决 1.1 Jmeter如何针对https协议进行接口测试? 解决方法: 协议更改为:https,端口号更改为443;Jmeter默认的是:http协议,端口号是:80 1.2 Jmeter如何解决默…...

蓝牙单连接和多连接知识
蓝牙单连接和多连接知识 生活中蓝牙连接多路蓝牙的情况越来越多,下面介绍下单连接和多连接的知识,供大家参考 一:蓝牙单连接 蓝牙单连接也称为Point-to-Point 点对点连接,是最常见的蓝牙连接场景,如手机<–>车载蓝牙。&…...

Mongodb—查询数据报错 Sort operation used more than the maximum 33554432 bytes of RAM
线上服务的MongoDB中有一个很大的表数据有十几万条。然后报了下面这个错误: “exception”:”org.springframework.data.mongodb.UncategorizedMongoDbException”, “message”:”Query failed with error code 96 and error message ‘Executor error during find command:…...

Java内存异常和垃圾回收机制
内存溢出异常 Java会存在内存泄漏吗?请简单描述 内存泄漏是指不再被使用的对象或者变量一直被占据在内存中。理论上来说, Java是有GC垃圾回收机制 的,也就是说,不再被使用的对象,会被GC自动回收 掉,自动…...

linux系统挂载逻辑卷和扩展逻辑卷组
fdisk /dev/vdb fdisk /dev/vdc在分区后需要修改分区类型为 8e,操作过程类似: [rootlocal ~] $ fdisk /dev/xvdb #### 选择磁盘 Command (m for help): m #### 帮助 Command actiona tog…...
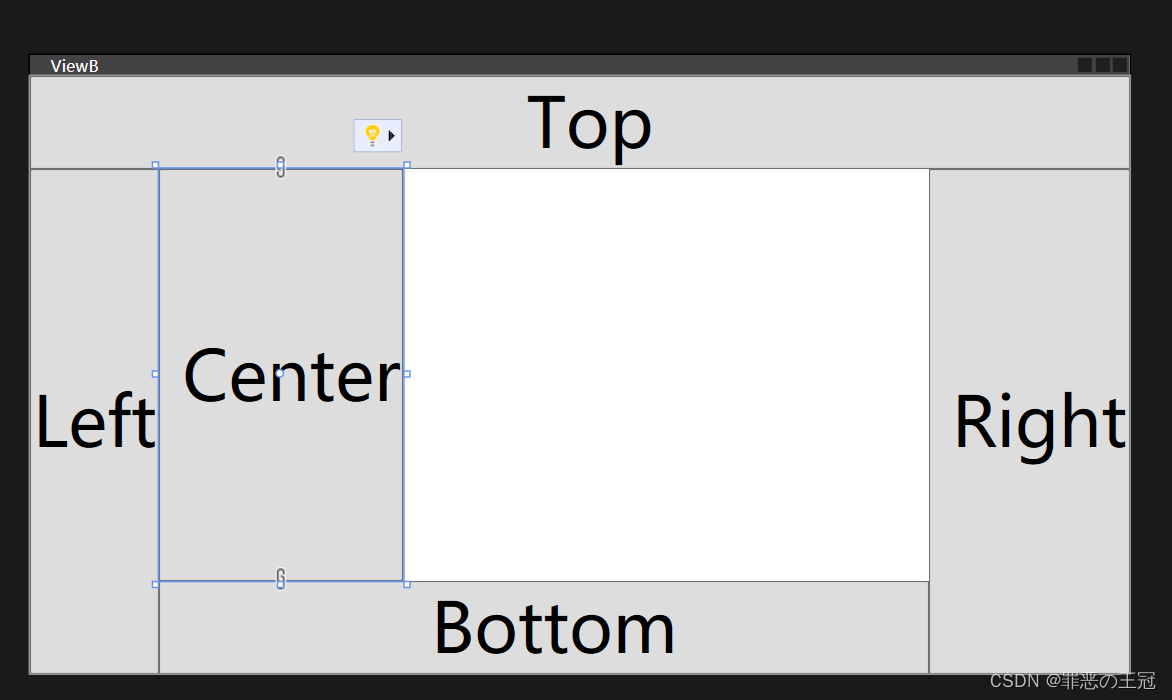
WPF:WPF原生布局说明
前言 WPF在国内讨论度很小,我在这里记录一下WPF简单的原生控件是如何使用的,顺便回忆一下WPF的基础知识,有些忘记的比较厉害了 WPF简介 WPF是微软推出的桌面UI软件,是我觉得最早实现MVVM(数据驱动事务)&…...
SpringMVC常用注解用法
Spring MVC是基于Servlet API构建的原始Web框架。 MVC是Model View Controller的缩写即视图模型控制器,是一种思想,而Spring MVC是对该思想的具体实现。关于SpringMVC的学习我们需要掌握用户和程序的连接、获取参数以及返回数据三大部分。而这三大功能的…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...
