leecode654——最大二叉树
leecode最大二叉树
🌻题目要求:
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
创建一个根节点,其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
🌻思路一:递归
🌻思路二: 单调栈
使用递归虽然每次对数组进行了拆分,但是会对数组中的元素也进行多次遍历,那么会不会有一种方式,可以仅通过一次遍历就可以得出最终结果。
单调栈的思路:
🔵(1)如果栈顶元素大于待插入的元素,那么直接入栈;
🔵(2)如果栈顶元素小于待插入的元素,那么栈顶元素出栈
在对比节点的同时,也要进行二叉树得到构造,即:
🔵(1)如果栈顶元素大于待插入的元素,则栈顶元素.right=待插入元素
🔵(2) 如果栈顶元素小于待插入的元素,则待插入元素.left=栈顶元素。
图来自:leecode大佬思路
🌻 以nums=[3,2,1,6,0,5]为例,看单调栈如何创建二叉树。
🌿首先,对于数组前3个元素,满足Node(3)>Node(2)>Node(1),所以3个元素直接入栈,并且构造二叉树Node(3).right=Node(2),Node(2).right=Node(1)
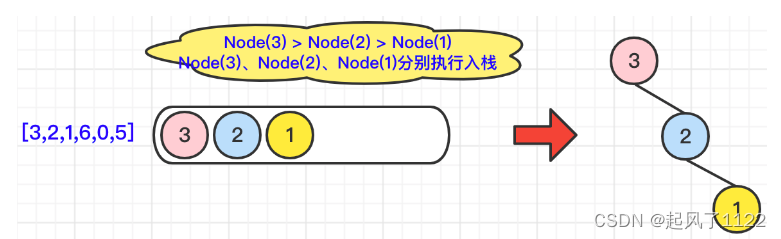
🌿当遍历到Node(6)时,由于Node(1)<Node(6),所以Node(1)出栈,并且执行Node(6).left=Node(1),又由于Node(2)<Node(6),所以Node(2)也出栈,并且执行Node(6).left=Node(2),
🔔注意:此时Node(6)的左节点从Node(1)变成了Node(2),由于Node(3)<Node(6),所以Node(6).left=Node(3),注意:此时Node(6)的左节点从Node(2)变成了Node(3),由于栈中没有元素可以出栈 了,没有可以和Node(6)对比的元素了,因此Node(6)入栈。
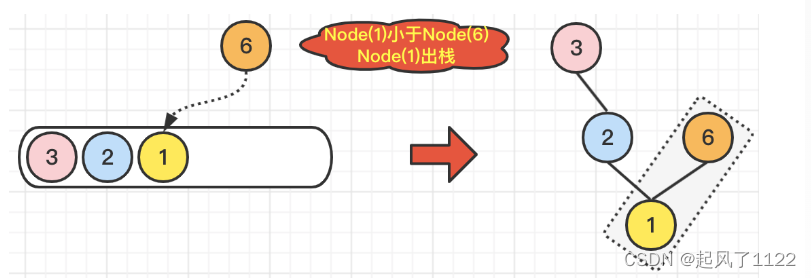

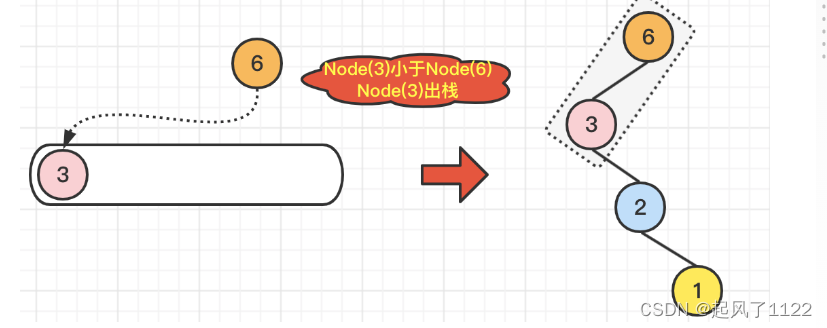
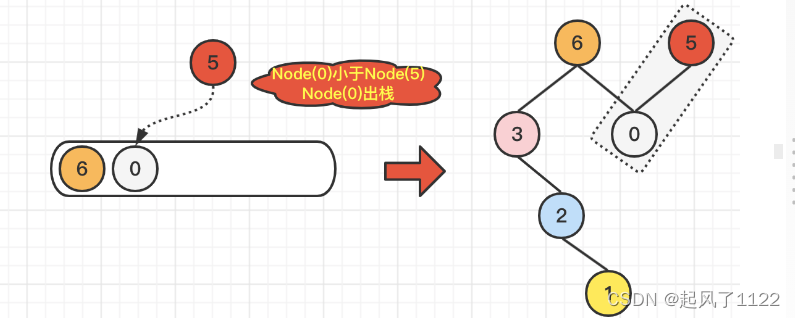
🌿我们继续遍历到Node(0),由于Node(0)小于栈顶元素Node(6),所以Node(0)直接入栈就可以了。但是,别忘记维护一下二叉树,也就是说,配置一下Node(6).right = Node(0)。具体操作,如下图所示:
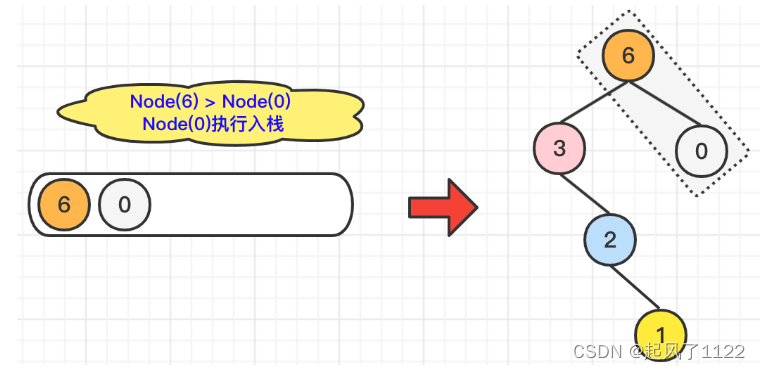
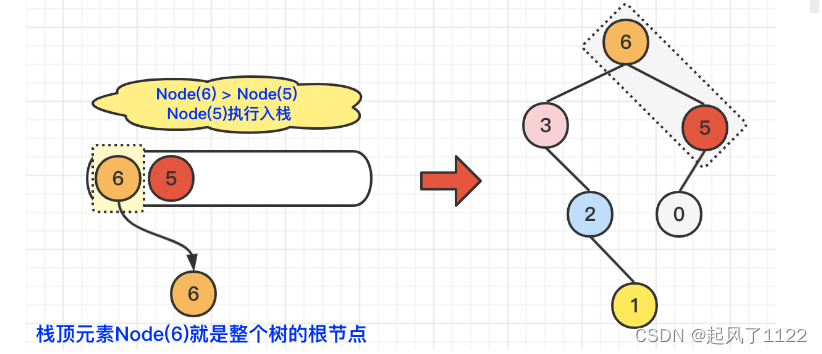
🌿最后,我们遍历到了Node(5),由于Node(5)大于当前栈顶元素Node(0),所以Node(0)执行出栈操作,并维护二叉树结构Node(5).left = Node(0);在对比Node(5)小于当前栈顶元素Node(6),所以,Node(5)直接入栈即可。维护二叉树结构Node(6).right = Node(5)。具体操作,如下图所示:
🌻代码如下:
class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {Deque<TreeNode> q=new ArrayDeque<>();for(int i=0;i<nums.length;i++){TreeNode node=new TreeNode(nums[i]);while(!q.isEmpty()){TreeNode topNode=q.peekLast();if(topNode.val>node.val){q.addLast(node);topNode.right=node;break;}else{q.removeLast();node.left=topNode;}}if(q.isEmpty()){q.addLast(node);}}return q.peek();}
}
🌻补充:
1.单调栈
🟢单调栈是一种特殊的栈数据结构,它的特点是栈内的元素保持单调递增或单调递减的顺序。具体来说,单调栈可以分为单调递增栈和单调递减栈两种类型。
在使用单调栈时,通常需要解决与元素的大小关系相关的问题,例如找到数组中元素的下一个更大元素、下一个更小元素等。单调栈提供了一种高效的方法来解决这些问题。
🟢单调递增栈的特点是栈内的元素从栈底到栈顶保持递增的顺序,而单调递减栈则是栈内的元素从栈底到栈顶保持递减的顺序。
🟢使用单调栈的好处包括:
快速找到某个元素的下一个更大或更小元素。通过保持栈内元素的单调性,可以在 O(1) 的时间复杂度内找到下一个更大或更小的元素,而无需遍历整个数组或其他数据结构。
节省空间和时间复杂度。相比其他数据结构,单调栈通常可以以更少的空间和更低的时间复杂度来解决一些特定的问题。解决一些特定的问题。单调栈常用于解决与元素大小相关的问题,如找到数组中元素的下一个更大元素、下一个更小元素,或者计算数组中每个元素的距离最近的更大或更小元素等。
2.单调栈和普通栈的区别
🟢 单调性要求:
单调栈要求栈内的元素保持单调递增或单调递减的顺序,而普通栈没有这个要求,可以存储任意顺序的元素。
🟢入栈规则:
单调栈的入栈规则与普通栈相同,即将元素压入栈顶。但是,单调栈在入栈时需要根据单调性进行调整。对于单调递增栈,当有新的元素要入栈时,需要将栈内比该元素小的元素全部出栈;对于单调递减栈,则是将栈内比该元素大的元素全部出栈。
🟢出栈规则:
单调栈的出栈规则与普通栈相同,即将栈顶元素弹出。在单调栈中,出栈操作通常与寻找下一个更大或更小元素有关,具体出栈规则会根据问题的需求而定。
🟢使用场景:
普通栈可以用于存储和操作任意类型的数据,适用于一般的栈操作。而单调栈主要应用于一些特定问题,例如找到数组中元素的下一个更大或更小元素、计算数组中每个元素的距离最近的更大或更小元素等,这些问题与元素的大小关系有关,而单调栈提供了一种高效的解决方法。
相关文章:

leecode654——最大二叉树
leecode最大二叉树 🌻题目要求: 给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建: 创建一个根节点,其值为 nums 中的最大值。 递归地在最大值 左边 的 子数组前缀上 构建左子树。 递归地在最大值 右边 的…...

【笔试强训选择题】Day12.习题(错题)解析
作者简介:大家好,我是未央; 博客首页:未央.303 系列专栏:笔试强训选择题 每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!! 文章目录…...

边缘计算与开放源代码的完美结合
随着人工智能、大数据和物联网等技术的快速发展,边缘计算已经成为一种普遍使用的计算方式,尤其是在物联网领域。与此同时,越来越多的开放源代码项目也在不断涌现,这些项目为边缘计算提供了更多的选择和灵活性。那么,边…...

边缘计算网关在储能系统中的应用——提高储能系统的安全性和稳定性
随着全球能源消耗和环境保护意识的不断提高,储能技术逐渐成为了各国电力系统中的重要一环。而作为储能技术中的关键设备之一,边缘计算网关在储能系统中的应用也越来越受到关注。本文将从边缘计算网关的定义、特点以及其在储能行业中的应用三个方面来介绍…...
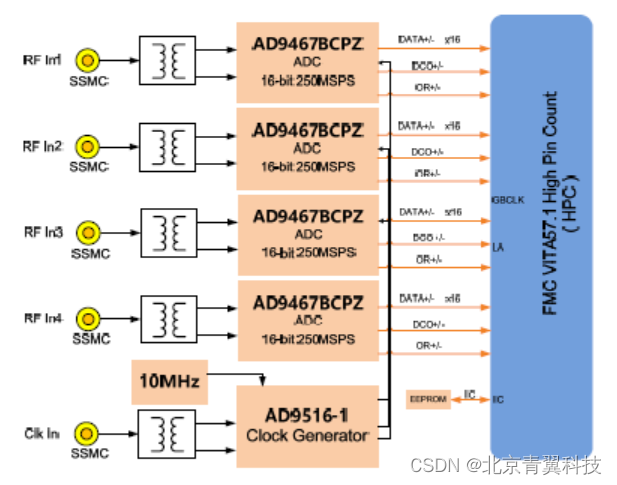
【FMC136】AD9467之4通道 250MSPS 采样率16位AD 采集子卡模块得设计原理图中文资料
板卡概述 FMC136 是一款4 通道250MHz 采样率16 位AD 采集FMC子卡,符合VITA57 规范,可以作为一个理想的IO 模块耦合至FPGA前端,4 通道AD 通过高带宽的FMC 连接器(HPC)连接至FPGA 从 而大大降低了系统信号延迟。该板卡支…...
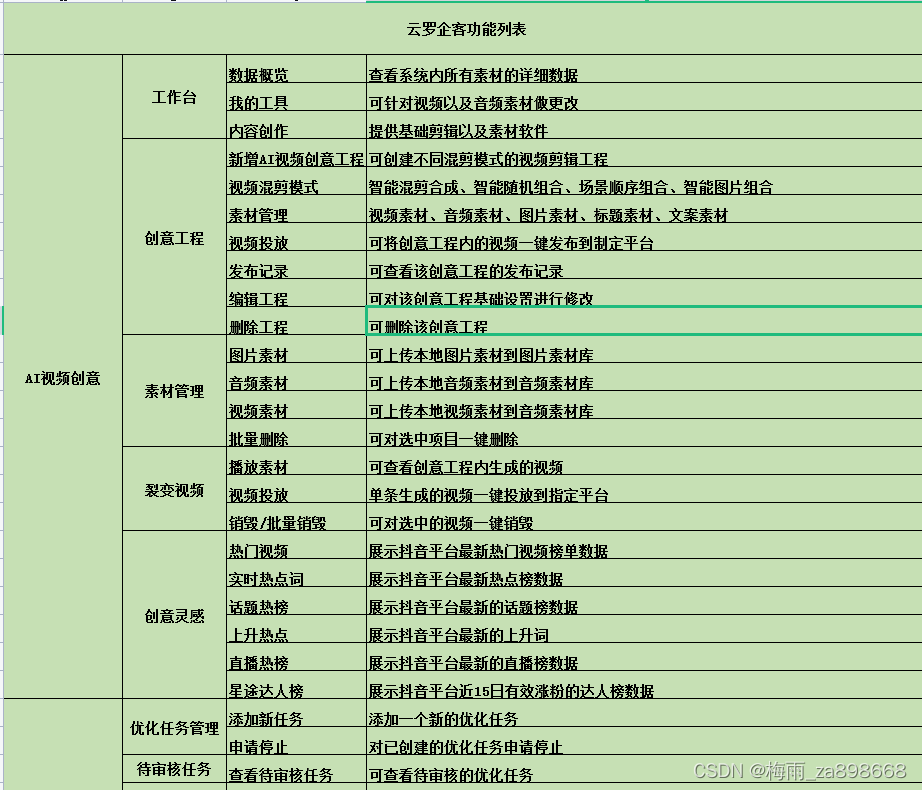
抖音SEO矩阵系统源码开发(一)
抖音seo矩阵营销系统/抖音SEO矩阵号管理系统/抖音霸屏源码开发搭建,抖音官方团队大力推广抖音SEO生态,我们应如何布局开发抖音SEO矩阵系统,来达到账号排名优化的效果,很显然,账号关键词起到了很关键的作用。首先&#…...
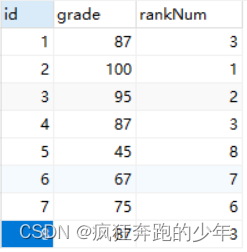
Mysql实现对某一字段排序并将排名写入另一字段
文章目录 前言一、数据库表结构和样例数据二、排名操作1.普通排名2.无间隔排名3.有间隔排名 总结 前言 最近业务上碰到这样一个需求,需要对表按照某一个字段进行排序,并且将得到的排名写入对应的排名字段。这个需求于我而言确实没有遇到过,好…...

vector容器 [上]
目录 一、 对于vector的介绍 二、vector的定义 0x01 无参构造 0x02 构造并初始化n个val 0x03 使用迭代器进行初始化构造 0x04 拷贝构造 0x05 比较 三、 vector的遍历 0x01 push_back() 0x02 operator[] 和at() 0x03 遍历 四、vector 容量空间 0x01 max_size : 返回v…...

React Native技术探究:开发高质量的跨平台移动应用的秘诀
作为一个跨平台移动应用开发框架,React Native在开发过程中能够有效提高开发效率、降低开发成本、缩短上线时间,因此备受开发者的欢迎。然而,如何使用React Native开发出高质量的跨平台移动应用呢?本文将探究这个问题,…...
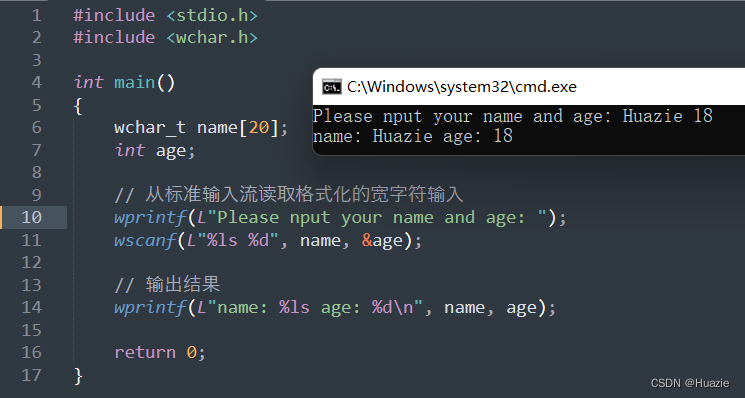
C语言函数大全-- w 开头的函数(2)
C语言函数大全 本篇介绍C语言函数大全-- w 开头的函数 1. wcstok 1.1 函数说明 函数声明函数功能wchar_t *wcstok(wchar_t *wcs, const wchar_t *delim, wchar_t **ptr);用于将一个长字符串拆分成几个短字符串(标记),并返回第一个标记的地…...

kafka启动创建topic报错:zookeeper is not a recognized option
当前使用版本:kafka_2.13-3.4.0 使用老版本的创建topic的命令,是用zookeeper来创建,但是报错如下 D:\Software\Doument\kafka_2.13-3.4.0> .\bin\windows\kafka-topics.bat --create --zookeeper localhost:2181 --replication-factor 1 …...

11个超好用的SVG编辑工具
SVG的优势在于SVG图像可以更加灵活,自由收缩放大而不影响图片的质量,一个合适的SVG编辑工具能够让你的设计事半功倍,下面就一起来看看这些冷门软件好用在哪里。这11个超好用的SVG编辑工具依次为:即时设计、Justinmind、Sketsa SVG…...
低代码平台:10分钟从入门到原理
导航目录 一、低代码概念 二、优势及局限 三、基础功能及搭建 1、业务流程 2、用户权限 3、统计图表 四、使用感受 五、总结 传统的软件研发方式目前并不能很好地满足企业的需求:人员成本高、研发时间长、运维复杂。这时低代码工具的出现为快速开发软件提供…...

【JavaScript】如何获取客户端IP地址?
使用这个库:request-ip 它按照如下顺序获取请求的IP地址: X-Client-IPX-Forwarded-For (Header may return multiple IP addresses in the format: “client IP, proxy 1 IP, proxy 2 IP”, so we take the first one.)CF-Connecting-IP (Cloudflare)F…...
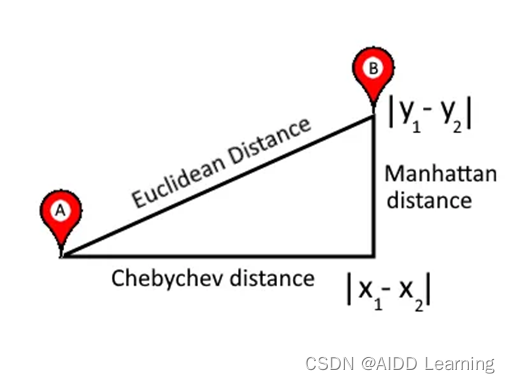
数据科学中使用的17 种相似性和相异性度量之欧氏距离
目录 1简介 2距离函数 2.1 L2范数(欧氏距离) 1简介 在数据科学中,相似性度量是一种衡量数据样本如何相互关联或相互接近的方法。另一方面,相异性度量是告诉数据对象有多少是不同的。此外,当相似的数据样本被分组到一…...

朋友去华为面试,轻松拿到30K的Offer,羡慕了......
最近有朋友去华为面试,面试前后进行了20天左右,包含4轮电话面试、1轮笔试、1轮主管视频面试、1轮hr视频面试。 据他所说,80%的人都会栽在第一轮面试,要不是他面试前做足准备,估计都坚持不完后面几轮面试。 其实&…...

MySQL入门第五课:数据更新
数据更新 1 插入 插入表数据 insert into 表名 (字段列表) values(值列表) insert into 表名 set 字段名1 值1,字段名2值2 插入多个数据 insert into 表名 values(值1,值2,值3.....) 这里面的值与列索引是对应的 显示表数据 select * fr…...

ALSA子系统(十八)------指纹解锁动画提示声卡顿问题解析
你好!这里是风筝的博客, 欢迎和我一起交流。 很久没写kernel相关的东西了,主要是来到手机厂之后,大部分还是在Android上,Kernel虽然也有涉及,但毕竟只是有所涉及,主要业务逻辑还是在HAL之上&am…...

[230513] TPO72 | 2022年托福阅读真题第1/36篇 | 10:45
Invading Algae 目录 Invading Algae 全文 题目 Paragraph 1 P1 段落大意 问题1 Paragraph 2 P2 段落大意 问题2 *问题3* Paragraph 3 P3 段落大意 问题4 Paragraph 4 P4 段落大意 Paragraph 5 P5 段落大意 *问题5* *问题6* 问题7 问题8 问题9…...
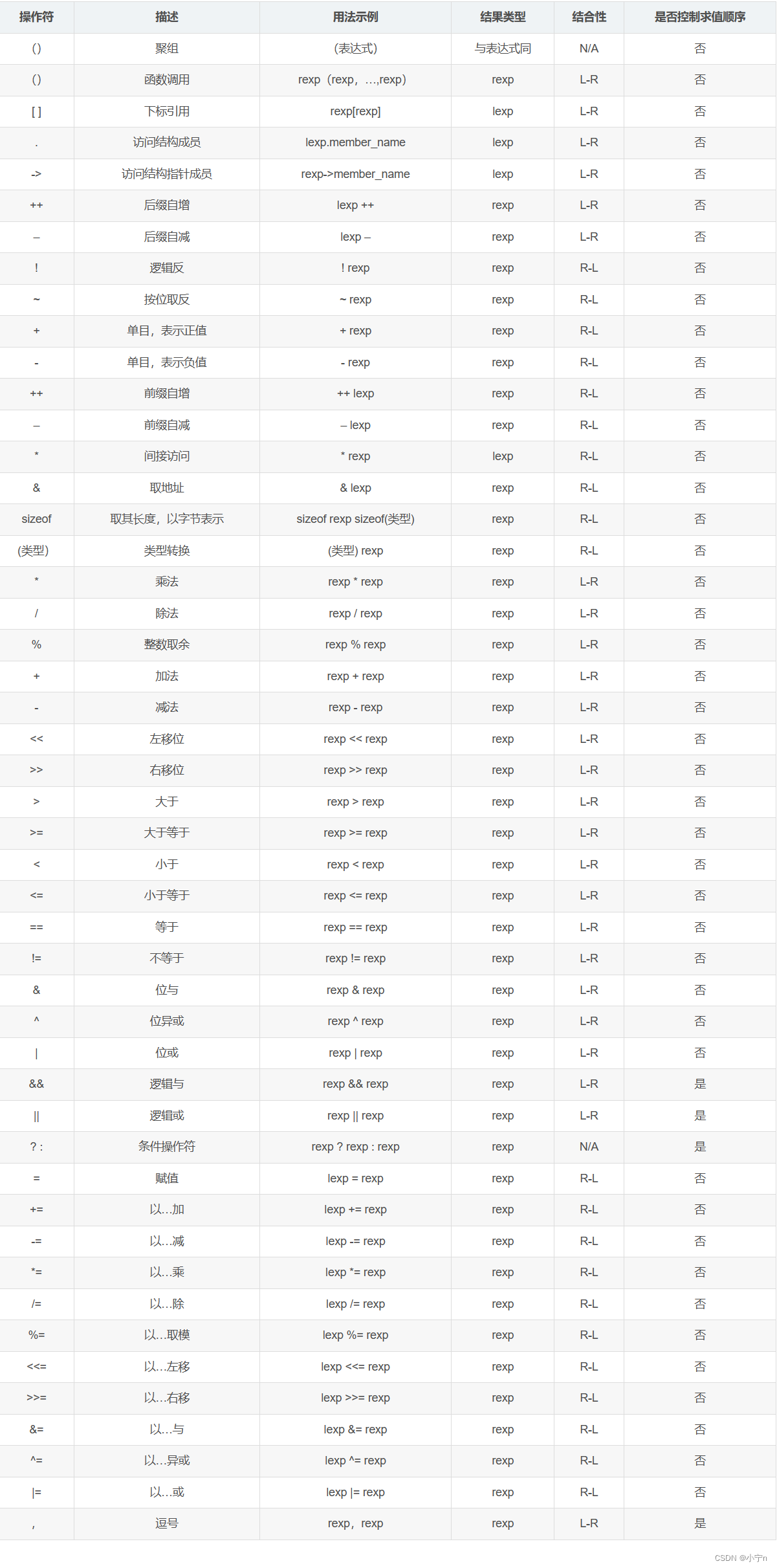
操作符详解
目录 操作符分类 算术操作符 - * / % 二进制 二进制总结 移位操作符(操作数只能为整数) << >> 位操作符(操作数必须为整数) & | ^ 面试题 赋值操作符 复合赋值符 单目操作符 单目操作符介绍…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...
