2023 年第八届数维杯数学建模挑战赛 赛题浅析
为了更好地让大家本次数维杯比赛选题,我将对本次比赛的题目进行简要浅析。本次比赛的选题中,研究生、本科组请从A、B题中任选一个 完成答卷,专科组请从B、C题中任选一个完成答卷。这也暗示了本次比赛的难度为A>B>C
选题人数初步估计也是B>C>A
下面给大家带来每个问题简要的分析,以方便大家提前选好题目。
A 题 河流-地下水系统水体污染研究
该问题,初步来看属于物理方程类题目,难度较大。需要我们通过查阅相关文献和资料,分析并建立河流-地下水系统中有机污染物的对流、弥散及吸附作用的数学模型 。通过简单的查阅资料(其中公式为latex输入语言,大家看不懂的,可以直接看图片)
河流-地下水系统中有机污染物的对流、弥散及吸附作用的数学模型可以参考以下公式:
$$\frac{\partial C}{\partial t}+\nabla\cdot(\mathbf{v}C)=D\nabla^2C-\lambda C+R$$
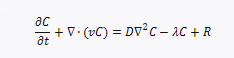

其中,$C$是有机污染物的浓度,$\mathbf{v}$是地下水的速度,$D$是水动力弥散系数,$\lambda$是有机污染物的降解速率,$R$是有机污染物的源项或汇项。
对于吸附作用,可以采用双模式吸附模型,即:
$$S=\frac{K_dC}{1+bC}+\frac{S_0bC}{1+bC}$$
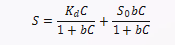
其中,$S$是沉积物上的吸附量,$K_d$是线性吸附系数,$S_0$是最大吸附容量,$b$是吸附表面亲和性常数。
对于阻滞作用,可以采用阻滞系数(R)来表示,即:
$$R=\frac{1}{1+\rho_b\frac{dS}{dC}}$$
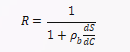
其中,$\rho_b$是沉积物的密度。
整体来看,难度较大,需要有较好的数学能力或者物理能力。问题二三将会后续问题分析中进行讲解。
B 题 节能列车运行控制优化策略
对于问题B问题一也是于A题相同,类似于物理微分方程模型,要解决这个问题,我们可以采用数值积分的方法,将列车在运行过程中的运动学方程和牵引力、制动力、阻力之间的关系相结合。以下是一个简单的 Python 程序,(要是大家有需要,我也可以编写对应的matlab代码)用于计算列车的运动学参数和能量消耗
import numpy as np
import matplotlib.pyplot as plt# Parameters
m = 176.3 * 1000 # Mass of the train (kg)
p = 1.08 # Rotational mass factor
v_max = 100 / 3.6 # Maximum velocity (m/s)
f_davis = lambda v: 2.0895 + 0.0098*v + 0.006*v**2 # Davis resistance equation
F_max = 310 * 1000 # Maximum traction force (N)
B_max = 760 * 1000 # Maximum braking force (N)
L = 5144.7 # Distance between A and B (m)
delta_t = 0.01 # Time step (s)# Initial conditions
x = 0 # Initial position (m)
v = 0 # Initial velocity (m/s)
t = 0 # Initial time (s)
E_kin = 0 # Initial kinetic energy (J)
E_pot = 0 # Initial potential energy (J)
E_loss = 0 # Initial energy loss (J)# Arrays for storing results
x_array = []
v_array = []
t_array = []
F_array = []
E_array = []# Simulation loop
while x < L:# Calculate accelerationF_net = F_max if x < L/2 else -B_max # Traction force or braking forceF_resist = f_davis(v) # Resistance forcea = (F_net - F_resist) / (m + p*v*v)# Calculate velocity and positionv += a * delta_tx += v * delta_tt += delta_t# Store resultsx_array.append(x)v_array.append(v)t_array.append(t)F_array.append(F_net if F_net > 0 else -F_resist) # Store positive force (traction) or negative force (braking)# Calculate energyE_kin = 0.5 * m * v**2E_pot = m * 9.8 * xE_loss += abs(F_resist * v * delta_t) # Accumulate energy lossE_array.append(E_kin + E_pot - E_loss)# Plot results
fig, axs = plt.subplots(2, 2, figsize=(12, 8))
axs[0, 0].plot(x_array, v_array)
axs[0, 0].set_xlabel("Distance (m)")
axs[0, 0].set_ylabel("Velocity (m/s)")
axs[0, 1].plot(x_array, F_array)
axs[0, 1].set_xlabel("Distance (m)")
axs[0, 1].set_ylabel("Force (N)")
axs[1, 0].plot(x_array, t_array)
axs[1, 0].set_xlabel("Distance (m)")
axs[1, 0].set_ylabel("Time (s)")
axs[1, 1].plot(x_array, E_array)
axs[1, 1].set在这种情况下,需要进一步考虑列车行驶过程中的各种因素,比如不同路段的限速和坡度、列车电机的动态特性以及储能装置的运用等等,以构建更加准确的模型。具体的建模过程需要综合考虑物理、数学、机械和电气等学科的知识,并采用合适的软件工具进行仿真和分析。
建模过程中需要考虑的因素很多,例如列车的动力学特性、牵引系统和制动系统的控制策略、能量管理系统等。在具体建模时,需要确定模型的输入和输出,以及各个子系统之间的关系,进而确定模型的结构和参数。同时,还需要考虑模型的有效性和可靠性,对模型进行验证和测试,以确保其能够准确地反映实际情况。
总的来说,建立列车运行模型是一个复杂的过程,需要充分考虑各种因素,采用合适的建模方法和软件工具,进行仿真和分析。同时,需要对模型进行验证和测试,以确保其能够准确地反映实际情况,并为实际应用提供有效的支持。
或者,我们也可以使用
根据搜索结果,列车运行建模方法可以分为以下几个步骤:利用Simulink或其他工具搭建列车运行的仿真模型,可以参考MATLAB提供的Powertrain Blockset和Vehicle Dynamics Blockset工具箱,或者使用专业软件如CarMaker、CarSim等。
设计列车运行的速度控制算法,根据列车的运行状态、线路参数、限速条件等信息,自动调整牵引/制动力,使列车沿最优速度-距离曲线运行。
通过仿真实验验证列车运行的速度控制效果,绘制速度-距离曲线、牵引制动力-距离曲线、时间-距离曲线与能量消耗-距离曲线等图形,分析列车运行的安全性、准时性、舒适性和经济性¹⁴。
程序的运行时间取决于仿真模型的复杂度、控制算法的效率、计算机的性能等因素,无法一概而论。需要获取不同到达时间的曲线时,可以通过调整控制算法中的参数或目标函数来实现。
C 题 宫内节育器的生产
C题为本次比赛最简单的一道题目,可惜选题受限。下面主要讲解一下各问解题思路。
问题一,分析两个医院的临床数据有无显著性差异,即进行显著性分析,相应的SPSS、matlab 、python各个软件都是可以实现的。
import pandas as pd
import numpy as np
import scipy.stats as stats# 读取数据
data = pd.read_csv('data.csv')# 计算相关系数和P值
corr_matrix = data.corr()
p_matrix = np.zeros(corr_matrix.shape)
for i in range(corr_matrix.shape[0]):for j in range(corr_matrix.shape[1]):pearson_coef, p_value = stats.pearsonr(data.iloc[:, i], data.iloc[:, j])p_matrix[i, j] = p_value# 显示相关系数矩阵和P值矩阵
print("Correlation Matrix:")
print(corr_matrix)
print("P-Value Matrix:")
print(p_matrix)# 进行显著性检验
threshold = 0.05 # 设置显著性水平
sig_matrix = p_matrix < threshold # 判断P值是否小于显著性水平
print("Significant Matrix:")
print(sig_matrix)这里只考虑了相关性的显著性检验,实际上显著性分析还可以涉及到多元回归分析、方差分析、卡方检验等方法。在实际应用中,我们需要根据具体问题选择合适的显著性检验方法,并使用相应的工具库进行分析。
问题二、分析受试者的身体指标与随访主诉情况的联系,典型的关联性分析。根据情况选择合适的方法即可。

问题三、分析 VCu260 与 VCu380 记忆型宫内节育器的质量哪个更优。可以理解为优化模型,设置0-1变量为决策变量对最优节育器进行求解,也可以建立综合评价模型,具体选择因对而异。
相关文章:

2023 年第八届数维杯数学建模挑战赛 赛题浅析
为了更好地让大家本次数维杯比赛选题,我将对本次比赛的题目进行简要浅析。本次比赛的选题中,研究生、本科组请从A、B题中任选一个 完成答卷,专科组请从B、C题中任选一个完成答卷。这也暗示了本次比赛的难度为A>B>C 选题人数初步估计也…...
Spring Boot单元测试
什么是单元测试? 单元测试(unit testing),是指对软件中的最小可测试单元进行检查和验证的过程就叫单元测试。 单元测试是开发人员编写的一小段代码,用于检验被测代码的一个很小的、很明确的(代码) 功能是否正确。执行单元测试就是为了证明某…...

实景三维浪潮翻涌,新技术“席卷”石家庄!
5月11日,“全自主、全流程、全覆盖”2023实景三维新技术研讨会石家庄站暨航测与遥感学术交流会在石家庄凯旋金悦大酒店圆满举行。 本次会议由中国测绘学会、中国地理信息产业协会指导,河北省测绘学会、河北省地理信息产业协会主办,武汉大势智…...

【Python】使用小脚本
本文整理了我在学习和工作中用到的实用python脚本,希望也能帮助到需要的小伙伴~ 文章目录 视频格式转换顺序遍历文件夹中的文件 视频格式转换 安装视频处理库moviepy pip install moviepy安装FFmpeg(FFmpeg是一个开源的多媒体框架,moviepy…...

技术日志2023-5-18
1、Java远程调试 可参考:https://kefeng.wang/2018/03/06/idea-remote-debug/ 2、用户中心这样的基础项目有什么用,感觉非常鸡肋。 今天开发讨论中涉及到了用户中心,感觉在项目中使用用户中心只是给业务系统发一个token,业务系…...

JUC之锁
公平锁、非公平锁 公平锁指的是多线程按照申请锁的顺序来获取锁; 非公平锁指的是多线程不按照申请锁的顺序来获取锁。可能会出现优先级反转(后者居上) 公平锁为了保证线程申请顺序,势必要付出一定的性能代价,因此其吞…...

C++中的 cout 和 printf 用法
文章目录 前言cout & printfexampleprintf输出string字符串总结 前言 C是一种面向对象的编程语言,它继承了C语言的特点,同时也增加了许多新的特性。在C中的cout 和 printf是两种常用的输出函数,它们都可以将数据显示在屏幕上,…...
Maven基础使用
Maven 学习目标 理解Maven的用途掌握Maven的基本操作掌握Maven如何创建Web项目 Maven是什么 面临问题 在学习Maven之前,我们先来看一下我们现在做的项目都有哪些问题。假设你现在做了一个crm的系统,项目中肯定要用到一些jar包,比如说myb…...

【C++ 入坑指南】(06)运算符
文章目录 一、算术运算符二、赋值运算符三、比较运算符四、逻辑运算符五、算法题5.1、拆分位数 运算符是一种告诉编译器执行特定的数学或逻辑操作的符号。C 内置了丰富的运算符,并提供了以下类型的运算符: 运算符类型作用算术运算符用于处理四则运算赋值…...

了解一下js中的函数式编程
js中的函数式编程是一种编程范式,它将函数作为一等公民来使用。 在函数式编程中,函数是一种特殊的对象,可以赋值给变量、作为参数传递给其他函数、或作为其他函数的返回值。 函数式编程强调了函数的纯函数性,即函数输入相同时&a…...

动态HTTP代理在linux里的使用
动态HTTP代理是一种可以自动切换代理IP地址的代理方式,可以有效地绕过一些限制访问的网站。在Linux系统中,可以使用Privoxy和Proxychains来实现动态HTTP代理。 以下是在Linux中使用动态HTTP代理的步骤: 1. 安装Privoxy和Proxychains 在终端中…...

软考证书值得考吗?怎么考?
软考证书是什么?有什么用处?必须先明确这两个问题,才能有复习和考取的动力。怎么考过?这是第二步要着重解决的问题。今天详细帮助大家分析一下。 软考是国家级考试,具有强大的权威性与公信力。 软考全称为计算机技术…...
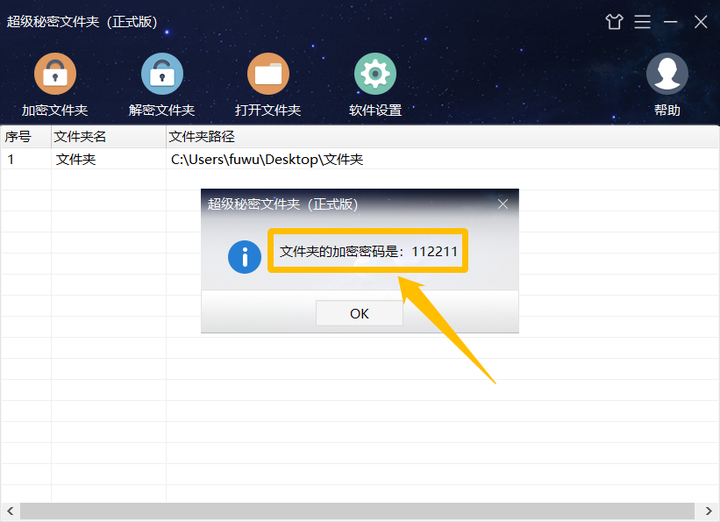
超级秘密文件夹忘记密码的解决办法
超级秘密文件夹是一款非常特殊的文件夹加密软件,它来无影去无踪,在安装后不会留下任何痕迹,只能通过软件热键才能打开。那么如果在使用过程中忘记了密码,这时我们该怎么办呢?下面我们就来了解一下。 首先,我…...
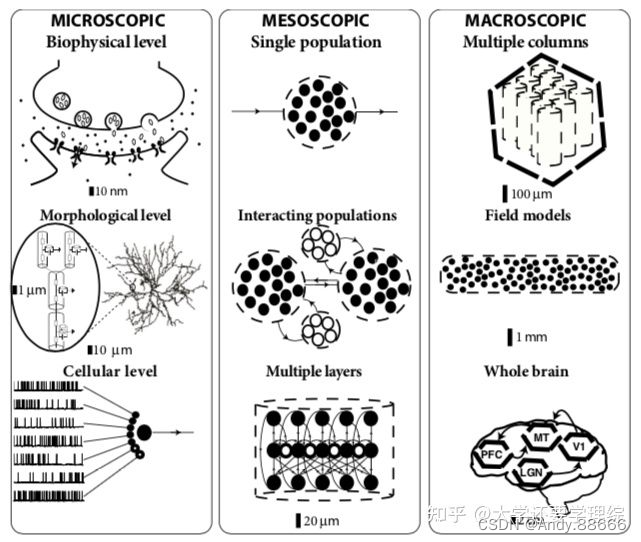
脑的物理系统
⼤脑模块化 人脑是一个复杂的网络,一般将大脑划分为不同的区域(即节点),并使用某种方法表征大脑区域之间的关系(即连接的边)来构建人脑网络。在功能磁共振成像(fMRI)数据的网络模型…...
-------------------c++实现)
1054. 距离相等的条形码(leetcode,堆问题,priority_queue)-------------------c++实现
1054. 距离相等的条形码(leetcode,堆问题,priority_queue)-------------------c实现 题目表述 在一个仓库里,有一排条形码,其中第 i 个条形码为 barcodes[i]。 请你重新排列这些条形码,使其中任意两个相…...

QT开发实战-动态壁纸软件
动态壁纸软件开发 项目源代码在下面链接获取: ----------------------------- 开发者:CodeSharkSJ 希望此项目能加强你对Qt的应用 文章目录 项目图与开发环境核心技术原理自定义窗口程序UI布局背景绘制样式表基本实现QWebEngineQMedia使用系统托盘隐藏记忆功能应用程序打包 …...
)
Netty核心组件模块(一)
1.Bootstrap和ServerBootstrap 1>.Bootstrap意思是引导,一个Netty应用通常由一个Bootstrap开始,主要作用是配置整个Netty程序,串联各个组件,Netty中Bootstrap类是客户端程序的启动引导类,ServerBootstrap是服务端启动引导类; 2>.常见的方法有: ①.public ServerBootstr…...
Robot Framework+Jenkins持续集成UI自动化项目
使用Robot Framework框架可进行Web端和APP端的UI自动化测试,为方便定时执行,可将Robot Framework的自动化项目持续集成至Jenkins平台,具体的操作步骤如下: 安装Jenkins的步骤如下: 手把手教小白安装Jenkins_程序员馨馨…...
【ROS】ROS1编程速览
1、简述 很多项目已经转向ROS2,本人作为ROS小白从ROS1开始学起,但是不会深入学习ROS1,只一带而过。 下面只了解一些ROS1中的概念和基本编程接口。 ROS1中有两种通信模式:话题模式和服务模式,区别如下 2、话题模式 …...

探索智能化:TOOM解析未来稿件校验系统的技术进展与应用展望
在信息时代,随着大数据、人工智能和自然语言处理等技术的快速发展,稿件校验系统正朝着智能化的方向迈进。智能化的稿件校验系统能够更准确、高效地检测虚假信息、抄袭行为以及提升文章质量。本文将探讨智能化稿件校验系统的技术进展与应用展望࿰…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...
