索洛模型(二)
索洛模型(二)
文章目录
- 索洛模型(二)
- @[toc]
- 1 事实
- 2 假设
- 2.1 对生产函数的假设
- 2.2对投入要素的假设
- 3 索洛模型的动态学
- 3.1 k k k的动态学
- 3.2 平衡增长路径
- 4 储蓄率变化的影响
- 4.1 对产出的影响
- 4.2 对消费的影响
文章目录
- 索洛模型(二)
- @[toc]
- 1 事实
- 2 假设
- 2.1 对生产函数的假设
- 2.2对投入要素的假设
- 3 索洛模型的动态学
- 3.1 k k k的动态学
- 3.2 平衡增长路径
- 4 储蓄率变化的影响
- 4.1 对产出的影响
- 4.2 对消费的影响
索罗经济增长模型(Solow growth model),罗伯特·索罗(Robert Solow)所提出的发展经济学中著名的模型,又称作新古典经济增长模型、外生经济增长模型,是在新古典经济学框架内的经济增长模型。
1 事实
增长奇迹:国家的增长在长期中远远高于世界平均水平,从而导致该国在世界收入分,布中的排名迅速上升。日本以及东亚新兴工业化国家和地区(简称NIC)–韩国、中国台湾、新加坡和中国香港。
增长灾难:增长灾难则是指一个国家的增长远远低于世界平均水平的现象。
一般而言,长期增长对福利的影响会超过短期波动影响,但传统宏观经济学却习惯于关注短期波动。
2 假设
四个变量:产出( Y Y Y)、资本( K K K)、劳动( L L L)与知识或有效劳动( L L L),在任意时刻 t t t满足
Y ( t ) = F ( K ( t ) , A ( t ) L ( t ) ) (1.1) Y(t) = F(K(t),A(t)L(t)) \tag{1.1} Y(t)=F(K(t),A(t)L(t))(1.1)
注:这里 A A A与 L L L是以相乘的方式进入生产函数的, A L AL AL称为有效劳动,这种引入方式称为劳动增强或哈罗德中性。索罗模型的核心假设包括两个方面:
- 生成函数的假设
- 对要素投入的假设
2.1 对生产函数的假设
-
两个要素自变量(资本与有效劳动)的
规模报酬是不变的
F ( c K , c A L ) = c F ( K , A L ) , ∀ c ≥ 0 (1.2) F(cK,cAL) = cF(K,AL),\forall c \ge 0 \tag{1.2} F(cK,cAL)=cF(K,AL),∀c≥0(1.2)
这意味着经济规模足够大,使得专业分工能够的好处能最大限度利用 -
相对资本、劳动与知识来说,其他投入要素并不重要
-
索罗模型忽略土地与自然资源的作用
假定规模报酬不变的好处: 函数形式更加紧凑。在(1.2)中,令 c = 1 / A L c = 1/AL c=1/AL 得到
F ( K A L , 1 ) = 1 A L F ( K , A L ) (1.3) F(\frac{K}{AL},1) = \frac{1}{AL}F(K,AL)\tag{1.3} F(ALK,1)=AL1F(K,AL)(1.3)
其中 K / A L K/AL K/AL表示有效劳动平均资本量,而$ F(K,AL)/AL = Y/AL$表示单位有效劳动的平均产出。定义
Expected node of symbol group type, but got node of type cr
从而
y = f ( k ) (1.4) y =f(k)\tag{1.4} y=f(k)(1.4)
即把单位有效劳动平均产出写为单位有效劳动平均产出的函数。工人平均产出为
Y L = A ( Y A L ) = A f ( k ) \frac{Y}{L}=A(\frac{Y}{AL})=Af(k) LY=A(ALY)=Af(k)
函数(1.4)的经济含义是将经济体划分为 A L AL AL个小经济体,每个小经济体都包含1单位有效劳动与 k = K / A L k =K/AL k=K/AL单位资本,由于规模报酬不变,每个小经济体的产出都是原有经济体的 1 / A L 1/AL 1/AL。关于函数(1.4)还需要满足以下条件
1 资本边际产出
f ( 0 ) = 0 , f ′ ( k ) > 0 , f ′ ′ ( k ) < 0 f(0)=0,f^{\prime}(k)>0,f^{\prime\prime}(k)<0 f(0)=0,f′(k)>0,f′′(k)<0
由 F ( K , A L ) = A L f ( K / A L ) F(K,AL) = ALf(K/AL) F(K,AL)=ALf(K/AL)可得
∂ F ( K , A L ) ∂ K = A L f ′ ( K A L ) 1 A L = f ′ ( k ) \frac{\partial F(K,AL) }{\partial K} = AL f^{\prime}(\frac{K}{AL})\frac{1}{AL}=f^{\prime}(k) ∂K∂F(K,AL)=ALf′(ALK)AL1=f′(k)
即要求资本的边际产出为正,且边际产出随着资本的增加而下降。
2 稻田条件
lim k → 0 f ′ ( k ) = ∞ , lim k → ∞ f ′ ( k ) = 0 \mathop {\lim }\limits_{k \to 0} f^{\prime}(k) = \infty,\mathop {\lim }\limits_{k \to \infty} f^{\prime}(k) = 0 k→0limf′(k)=∞,k→∞limf′(k)=0
即当资本存量很小时,资本的边际产出非常大;当资本存量很大时,资本的边际产出非常小。其作用是保证经济路径不会发散。
例:柯布道格拉斯生产函数(Cobb-Douglas)
F ( K , A L ) = K α ( A L ) 1 − α , 0 < α < 1 F(K,AL) =K^\alpha (AL)^{1-\alpha},0<\alpha<1 F(K,AL)=Kα(AL)1−α,0<α<1
- 规模报酬不变
F ( c K , c A L ) = c α c 1 − α K α ( A L ) 1 − α = c F ( K , A L ) F(cK,cAL) =c^\alpha c^{1-\alpha}K^\alpha (AL)^{1-\alpha}=cF(K,AL) F(cK,cAL)=cαc1−αKα(AL)1−α=cF(K,AL)
2)稻田条件
f ( k ) = F ( K A L , 1 ) = ( K A L ) α = k α f(k)=F(\frac{K}{AL},1)=(\frac{K}{AL})^{\alpha}=k^{\alpha} f(k)=F(ALK,1)=(ALK)α=kα
于是
f ′ ( k ) = α > 0 , f ′ ′ ( k ) = − ( 1 − α ) α k α − 2 < 0 f^{\prime}(k)=\alpha>0,f^{\prime\prime}(k)=-(1-\alpha)\alpha k^{\alpha-2}<0 f′(k)=α>0,f′′(k)=−(1−α)αkα−2<0
2.2对投入要素的假设
-
时间是连续的,每个变量都是关于时间的连续函数
-
资本、劳动与知识的初始值已知,并严格大于0。劳动与知识都严格按照固定比率增长
L ˙ ( t ) = n L ( t ) , A ˙ ( t ) = g A ( t ) (1.5) \dot L(t)=nL(t),\dot A(t)=gA(t)\tag{1.5} L˙(t)=nL(t),A˙(t)=gA(t)(1.5)
其中 n n n与 g g g都是外生变量。
假设经济体为两部门封闭经济,则经济总体产出 Y Y Y被划分为消费 C C C与投资 I I I,即
Y = C + I = C + S Y= C+I = C+S Y=C+I=C+S
若产出 s s s份额被用于投资, ( 1 − s ) (1-s) (1−s)的份额用于消费,其中储蓄 s s s是外生给定的参数;先假设现有资本折旧率为 δ \delta δ,于是
K ˙ ( t ) = s Y ( t ) − δ K ( t ) (1.6) \dot K\left( t \right) = sY\left( t \right) - \delta K\left( t \right)\ \tag{1.6} K˙(t)=sY(t)−δK(t) (1.6)
其中 K ˙ ( t ) \dot K\left( t \right) K˙(t)表示资本存量变化率,$sY\left( t \right) 为资本存量因投资而增加的数量; 为资本存量因投资而增加的数量; 为资本存量因投资而增加的数量;\delta K\left( t \right)$表示资本存量折旧而减少的数量。
3 索洛模型的动态学
3.1 k k k的动态学
经济总量会随时间不断增长,着眼于分析单位有效劳动的平均资本存量 k k k要比分析未经调整的资本存量 K K K容易得多。由 k = K / A L k =K/AL k=K/AL,利用链式法则得
k ˙ ( t ) = K ˙ ( t ) A ( t ) L ( t ) − K ( t ) [ A ( t ) L ( t ) ] 2 [ A ( t ) L ˙ ( t ) + L ( t ) A ˙ ( t ) ] = K ˙ ( t ) A ( t ) L ( t ) − K ( t ) A ( t ) L ( t ) L ˙ ( t ) L ( t ) − K ( t ) A ( t ) L ( t ) A ˙ ( t ) A ( t ) (1.7) \begin{aligned} \dot{k}(t) &=\frac{\dot{K}(t)}{A(t) L(t)}-\frac{K(t)}{[A(t) L(t)]^{2}}[A(t) \dot{L}(t)+L(t) \dot{A}(t)] \\ \\ &=\frac{\dot{K}(t)}{A(t) L(t)}-\frac{K(t)}{A(t) L(t)} \frac{\dot{L}(t)}{L(t)}-\frac{K(t)}{A(t) L(t)} \frac{\dot{A}(t)}{A(t)} \end{aligned} \tag{1.7} k˙(t)=A(t)L(t)K˙(t)−[A(t)L(t)]2K(t)[A(t)L˙(t)+L(t)A˙(t)]=A(t)L(t)K˙(t)−A(t)L(t)K(t)L(t)L˙(t)−A(t)L(t)K(t)A(t)A˙(t)(1.7)
将(1.5)、(1.6)带入到(1.7)得到
k ˙ ( t ) = s Y ( t ) − δ K ( t ) A ( t ) L ( t ) − k ( t ) n − k ( t ) g = s Y ( t ) A ( t ) L ( t ) − δ k ( t ) − n k ( t ) − g k ( t ) (1.8) \begin{aligned} \dot{k}(t) &=\frac{s Y(t)-\delta K(t)}{A(t) L(t)}-k(t) n-k(t) g \\ \\ &=s \frac{Y(t)}{A(t) L(t)}-\delta k(t)-n k(t)-g k(t) \end{aligned} \tag{1.8} k˙(t)=A(t)L(t)sY(t)−δK(t)−k(t)n−k(t)g=sA(t)L(t)Y(t)−δk(t)−nk(t)−gk(t)(1.8)
最后根据 f ( k ) = Y / A L f(k) = Y/AL f(k)=Y/AL得
k ˙ ( t ) = s f ( k ( t ) ) − ( n + g + δ ) k ( t ) (1.9) \dot k(t) = sf(k(t))-(n+g+\delta)k(t) \tag{1.9} k˙(t)=sf(k(t))−(n+g+δ)k(t)(1.9)
该微分方程是索洛模型得关键方程,它表明单位有效劳动平均资本存量的变化率是由以下两项之差决定的:
-
s f ( k ( t ) ) sf(k(t)) sf(k(t)):单位有效劳动的平均产出是 f ( k ) f(k) f(k),用于投资的比率为 s s s,因此该项为单位有效劳动的
实际投资 -
( n + g + δ ) k ( t ) (n+g+\delta)k(t) (n+g+δ)k(t):它代表了使得 k k k保持在现有水平所需要视为必要投资量。为防止 k k k不断减少,需要
持平投资:A A A: 现有资本会折旧,折旧部分资本必须得到资本补偿能防止资本存量下降,即 δ k ( t ) \delta k(t) δk(t)
B B B: 有效劳动的数量增加,仅保持资本存量 K K K不变的投资(补偿折旧的投资)并不足以保持单位有效劳动的平均资本存量 k k k不变。有效劳动数量增长率为 n + g n+g n+g,资本存量增长率也必须是 n + g n+g n+g才能保持 k k k不变,即 ( n + g ) k ( t ) (n+g)k(t) (n+g)k(t)
由(1.9)式可知,若
- 实际投资 > > >持平投资, k ˙ ( t ) > 0 \dot k(t) >0 k˙(t)>0,即单位有效劳动平均资本存量上升;
- 实际投资 < < <持平投资, k ˙ ( t ) < 0 \dot k(t) <0 k˙(t)<0,即单位有效劳动平均资本存量下降;
- 实际投资 = = =持平投资, k ˙ ( t ) = 0 \dot k(t) =0 k˙(t)=0,即单位有效劳动平均资本存量不变;
将实际投资与持平投资视为有效劳动平均资本 k k k的函数,其中 ( n + g + δ ) k (n+g+\delta)k (n+g+δ)k与 k k k成正比,而实际投资 s f ( k ) sf(k) sf(k)等于一个常数乘以单位有效流动平均产出。由稻田条件可知,实际投资曲线与持平投资曲线一定会在 k ≠ 0 k\ne 0 k=0之外的点 k ∗ k^* k∗出仅一次相交,用 k ∗ k^* k∗表示实际投资等于持平投资时的 k k k值。
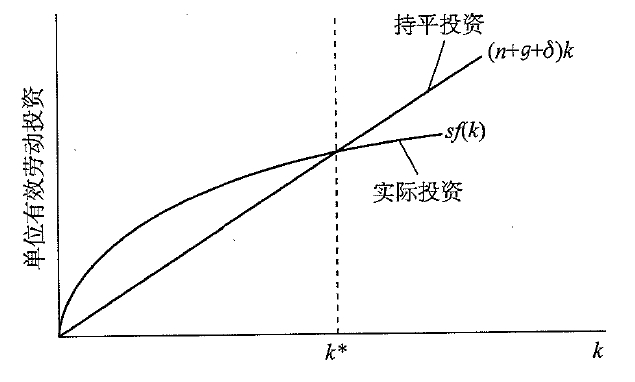
上图中, k ˙ \dot k k˙的值等于两条曲线之间的距离,将 k k k视为自变量, k ˙ \dot k k˙为因变量,于是得到关于 k k k的相位图。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LVxAMK5C-1684133736347)(null)]
关于相位图的解释:
- 当 k < k ∗ k< k^* k<k∗时,实际投资超过持平投资,因而 k ˙ \dot k k˙为正, k k k将不断上升;
- 当 k > k ∗ k> k^* k>k∗时,实际投资小于持平投资,因而 k ˙ \dot k k˙为负, k k k将不断下降;
- 当 k = k ∗ k = k^* k=k∗时,实际投资等于持平投资,因而 k ˙ \dot k k˙为0, k k k将保持不变,即 k ∗ k^* k∗;
因此无论 K K K位于何处,最终将会收敛到 k ∗ k^* k∗
3.2 平衡增长路径
当 k = k ∗ k = k^* k=k∗时,模型各个变量的具体变动为:
A :资本存量 K = A L k K = ALk K=ALk,由于 k = k ∗ k = k^* k=k∗,因此 K K K的增长率为 K ˙ / K = n + g \dot K/K = n+g K˙/K=n+g
B :有效劳动 A L AL AL的增长率也为( n + g n+g n+g)
C : 由于假定规模报酬不变,因此产出 Y Y Y的增长率也为 n + g n+g n+g
D: 工人平均资本 K / L K/L K/L的增长率为 g g g
E: 工人平均产出 Y / L Y/L Y/L的增长率为 g g g
证明A:
因为 K = A L k K = ALk K=ALk, k = k ∗ k = k^* k=k∗两边取对数得
l n K = l n A + l n L + l n k lnK = ln A+lnL+lnk lnK=lnA+lnL+lnk
同对时间求全微分
K ˙ K = A ˙ A + L ˙ L = g + n \frac{\dot K}{K} = \frac{\dot A}{A}+ \frac{\dot L}{L} = g+n KK˙=AA˙+LL˙=g+n
证明C:
Y = K α ( A L ) 1 − α ⇒ l n Y = α l n K + ( 1 − α ) l n A + ( 1 − α ) l n L ⇒ Y ˙ Y = α K ˙ K + ( 1 − α ) ( L ˙ L + A ˙ A ) = α ( n + g ) + ( 1 − α ) ( n + g ) = n + g \begin{aligned} Y& = K^\alpha(AL)^{1-\alpha} \Rightarrow lnY=\alpha lnK+(1-\alpha)lnA+(1-\alpha)lnL \\ \\ & \Rightarrow \frac{\dot Y}{Y} = \alpha\frac{\dot K}{K}+ (1-\alpha)(\frac{\dot L}{L} + \frac{\dot A}{A})= \alpha(n+g)+(1-\alpha)(n+g) =n+g \end{aligned} Y=Kα(AL)1−α⇒lnY=αlnK+(1−α)lnA+(1−α)lnL⇒YY˙=αKK˙+(1−α)(LL˙+AA˙)=α(n+g)+(1−α)(n+g)=n+g
证明D、E:利用两个变量之比的增长率等于两个变量增长率之差得 ( n + g ) − n = g (n+g)-n = g (n+g)−n=g
因此索洛模型表明:无论初始点在何处,经济总是收敛平衡增长路径,即模型中每个变量的增长率都是常数。在平衡增长路径上,工人平均产出的增长率是由技术进步唯一确定的。
4 储蓄率变化的影响
4.1 对产出的影响
假设储蓄率 s s s永久性提高,根据公式1.9得到 k ∗ k^* k∗提高,如下图所示
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fq587fh2-1684133736298)(null)]
下图展现了 t 0 t_0 t0时刻储蓄率变化对储蓄率 s s s,有效劳动平均资本增长率 k ˙ \dot k k˙,有效劳动平均资本 k k k,工人平均产出 Y / L Y/L Y/L和边际消费倾向 c c c的变化情况。
- 第一幅图表明储蓄率 s s s出现永久的提高
- 第二幅图由于 s s s增加导致实际投资大于持平投资,从而忽然 k ˙ > 0 \dot k>0 k˙>0,但持平投资的增长率保持不变,进而 k ˙ \dot k k˙逐渐缩小为0.
- 第三幅图由第二幅图解释。
- 第四幅图工人平均产出 Y / L = A f ( k ) Y/L = Af(k) Y/L=Af(k)的,其增长率只取决于技术进步率 g g g。随着储蓄率 s s s提高导致 k ˙ \dot k k˙短暂增加再缩小至0,因此 k k k也会增加从而 Y / L Y/L Y/L也会在 g g g的基础上提高,但后期依然取决于 g g g。第五幅图为第四幅图的对数形式
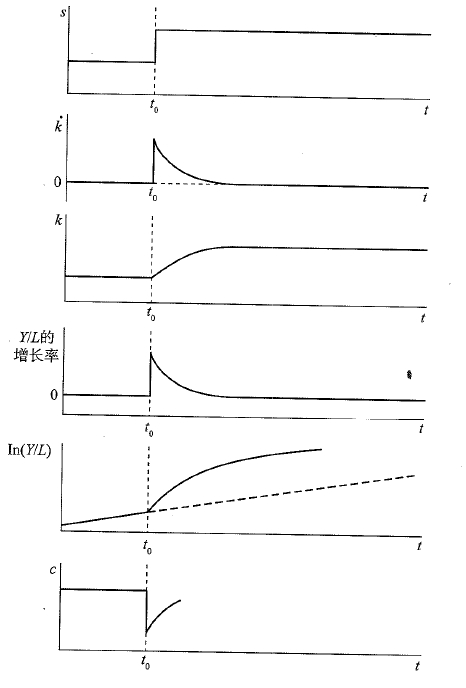
综上,储蓄率的变化只有水平效应,没有增长效应。事实上,在索洛模型中,仅有技术进步率才具有增长效应。
4.2 对消费的影响
单位有效劳动平均消费 c c c等于单位有效劳动的平均产出 f ( k ) f(k) f(k)乘以消费比例 1 − s 1-s 1−s,即 ( 1 − s ) f ( k ) (1-s)f(k) (1−s)f(k)。当储蓄率 s s s提高(阶梯式增加),而 k k k也提高(连续型增加),故 c c c出现断崖式降低,再从 t 0 t_0 t0时刻开始回升,见上第六幅图。但后期上升的幅度会超过原来的水平 c c c吗?
令 c ∗ c^* c∗为平衡增长路径上单位有效劳动平均消费,则
c ∗ = f ( k ∗ ) − ( n + g + δ ) k ∗ c^{*} = f(k^{*})-(n+g+\delta)k^{*} c∗=f(k∗)−(n+g+δ)k∗
因为平衡增长路径上 k ∗ = s f ( k ∗ ) − ( n + g + δ ) k ∗ k^{*}=sf(k^*)-(n+g+\delta)k^{*} k∗=sf(k∗)−(n+g+δ)k∗。显然 k ∗ k^{*} k∗由 n , g , δ n,g,\delta n,g,δ共同决定,那么根据链式法则
∂ c ∗ ∂ s = [ f ′ ( k ∗ ( s , n , g , δ ) ) − ( n + g + δ ) ] ∂ k ∗ ( s , n , g , δ ) ∂ s \frac{\partial c^{*}}{\partial s}=\left[f^{\prime}\left(k^{*}(s, n, g, \delta)\right)-(n+g+\delta)\right] \frac{\partial k^{*}(s, n, g, \delta)}{\partial s} ∂s∂c∗=[f′(k∗(s,n,g,δ))−(n+g+δ)]∂s∂k∗(s,n,g,δ)
其中 s s s增加会导致 k ∗ k^{*} k∗提高,因此储蓄率对消费的影响取决于单位有效劳动平均资本的边际产出与持平投资增长率的大小关系。
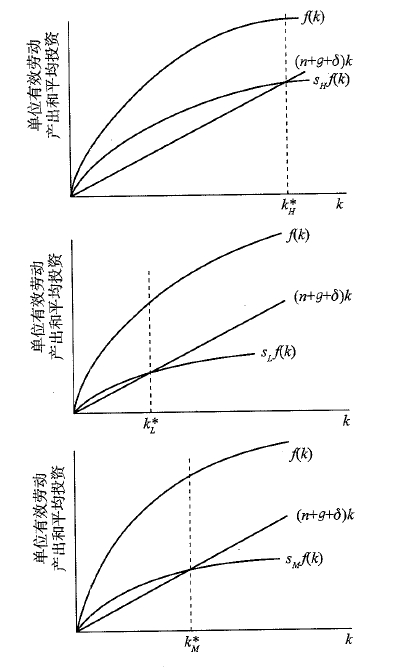
- 当 f ′ ( k ∗ ( s , n , g , δ ) ) > ( n + g + δ ) f^{\prime}\left(k^{*}(s, n, g, \delta)\right)>(n+g+\delta) f′(k∗(s,n,g,δ))>(n+g+δ)时(第一幅图),储蓄率提高促进消费增加
- 当 f ′ ( k ∗ ( s , n , g , δ ) ) < ( n + g + δ ) f^{\prime}\left(k^{*}(s, n, g, \delta)\right)<(n+g+\delta) f′(k∗(s,n,g,δ))<(n+g+δ)时(第二幅图),储蓄率提高抑制消费增加
- 当 f ′ ( k ∗ ( s , n , g , δ ) ) = ( n + g + δ ) f^{\prime}\left(k^{*}(s, n, g, \delta)\right)=(n+g+\delta) f′(k∗(s,n,g,δ))=(n+g+δ)时(第三幅图),储蓄率提高不对消费产生影响,但此时消费达到最大水平,此时的 k ∗ k^{*} k∗也称为资本存量的
黄金水平。
参考文献
[美] 戴维·罗默 . 高级宏观经济学(第四版) [M]. 上海财经大学出版社,2014
相关文章:

索洛模型(二)
索洛模型(二) 文章目录 索洛模型(二)[toc]1 事实2 假设2.1 对生产函数的假设2.2对投入要素的假设 3 索洛模型的动态学3.1 k k k的动态学3.2 平衡增长路径 4 储蓄率变化的影响4.1 对产出的影响4.2 对消费的影响 索罗经济增长模型(Solow growth model)&am…...
【多微电网】基于粒子群优化算法的面向配电网的多微电网协调运行与优化(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

使用Atmel Studio开发Arduino的ATmega328P单片机
摘要:我们知道Arduino开发板常用的芯片是Atmel公司生产的AVR微控制器系列。最常见的是ATmega328P,被广泛用于Arduino Uno开发板。其他常用的AVR芯片包括ATmega2560和ATmega32U4。使用Arduino平台开发AVR的单片机非常方便。Arduino IDE提供了一个非常简洁…...

docker基础命令
查找镜像 docker search nginx 拉取镜像 不指定镜像版本的话默认拉取最新的版本,可以在dockerhub上查看镜像的版本 dockerhub地址:Docker docker pull nginx docker pull nginx:1.23 查看镜像列表 docker images 打包镜像 打包的镜像可以迁移到其它的主机上部署 …...

数组名+1和数组名+1的区别
数组名和&数组名区别 #include <stdio.h>int main() {int a[5] {1,2,3,4,5};int *ptr (int *)(&a 1);printf("%d,%d,%d\n",*(a 4),*(ptr - 1),*ptr); // 2 5 为什么是5printf("数组a[4]的地址%p,(ptr-1)地址%p, ptr的地址%p",(a 4)…...
开放原子训练营(第三季)inBuilder低代码开发实验室初体验
一、活动介绍 开放原子训练营开启inBuilder低代码实验室活动。无论您是计算机行业相关从业者、低代码开发爱好者还是普通用户,都可以基于inBuilder低代码开发平台社区版(基于UBML开源项目的一个可以广泛使用的发行版),体验向导式、…...
)
sql数据定义语句(cascade,set,null,no action的区别)
(一)ADD 基本格式: ALTER TABLE <表名> ADD 新属性名 新属性类型 例:alter table s1 add tele char(12):增加一个电话号码(tele)属性 注: 新增的属…...

Java进程(基础)
基本概念 1、进程:程序的执行过程 2、线程:一个进程可以有单个线程也就是我们说的单线程,还可以有多个线程也就是我们说的多线程, 线程 1、当一个类继承了Thread类就可以当成一个线程用 2、我们会重写run方法写上我们自己的业务…...
Android之 Activity活动详解
一 四大组件 1.1 Activity组件,它一个单独的窗口,程序流程都必须在Activity中运行。 1.2 service组件,用于在后台完成用户指定的操作。 1.3 content provider组件,会为所有的应用准备一个内容窗口,并且保留数据库、…...

车载软件架构——闲聊几句AUTOSAR BSW(五)
我是穿拖鞋的汉子,魔都中坚持长期主义的工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 我们并不必要为了和谐,而时刻保持通情达理;我们需要具备的是,偶尔有肚量欣然承认在某些方面我们可能会有些不可理喻。该有主见的时候能掷地有声地镇得住场…...
APP图标尺寸规范一文了解清楚
在进行图标设计前,熟知手机 app 图标尺寸规范,能更好地去针对不同平台设计出更极致的图标。当前智能手机系统主要以 iOS 及 Android 为主,APP 图标是产品给用户的第一印象,图标视觉设计的美感与吸引力,与用户是否选择下…...

写给程序员Android Framework 开发,
前言 在 Android 开发者技能中,如果想进大厂,一般拥有较好的学历可能有优势一些。但是如果你靠硬实力也是有机会的,例如死磕Framework。Framework 知识广泛应用在Android各个领域中,重要性显而易见。 成为一名Android Framework…...

html实现一个一闪一闪的按钮,CSS实现一个一闪一闪的按钮,Css闪烁点标,css设置按钮层次感,css按钮美化,CSS按钮动画过渡,CSS按钮添加阴影
效果 动态 静态 实现 底部多加了几个过渡按钮 <!DOCTYPE html> <html><head><meta charset"UTF-8"><title></title><style>#app {margin: 2% auto;text-align: center;}.lay-btn-box {position: relative;display: …...
品优购项目学习记录04--列表页
文章目录 1.品优购项目列表页制作准备工作2.列表页header和nav修改2.1 秒杀logo的制作2.2 导航栏nav修改 3.列表页主体sk_container 1.品优购项目列表页制作准备工作 1.列表页面是新的页面,我们需要新建页面文件list.html 2.因为列表页的头部和底部基本一致&#x…...

script标签type值application/json,importmap和module
type(默认text/javascript) 该属性定义 script 元素包含或src引用的脚本语言。属性的值为 MIME 类型(媒体类型); 如果没有定义这个属性,脚本会被视作 JavaScript。 如果 MIME 类型不是 JavaScript 类型&a…...

基于ArcGIS实现陕西省1:250000比例尺地形图分幅和编号
1地形图的分幅与编号原理 我国1:1000000地形图的分幅采用国际1:1000000地图分幅标准,而其他比例尺地形图分幅以1:1000000比例尺地形图为基准进行分幅。每幅1:1000000地形图范围是经差6、纬差4;纬度60~ 76之间经差12、纬差4;纬度76~ 88之间经…...

校园安全,一键报警主机助力保障
校园安全,一键报警主机助力保障 随着社会发展和科技进步,校园安全问题日益受到重视。如何保障师生们的安全成为了学校一项重要任务。而校园可视一键报警主机就是一种非常有效的安保设备。 这种报警主机集合了视频监控、安全防范、数据处理等多个功能&a…...
)
RabbitMQ养成记 (7. 消息可靠性投递)
消息可靠性 什么是消息的可靠性呢?? 简单来说就是 你的消息发放给 exchange 这个过程中 有可能丢失或者失败 这时候需要一个回调机制来监控 发送结果 必要时还要返回信息。 rabbitmq 给我们提供了两种: 首先是生产者到exchange发送过程的监…...

SpringBoot配置连接两个或多个数据库
在Spring Boot应用中连接多个数据库或数据源可以使用多种方式,下面介绍两种常用的方法: 1、使用Spring Boot官方支持的多数据源配置 Spring Boot提供了官方支持的多数据源配置,可以简单地配置和管理多个数据源。 需要在application.proper…...

Python面试题汇总:高效备战技巧
Python面试题汇总:高效备战技巧 一、基础知识准备1 语言特点及优缺点2 数据类型3 运算符4 控制流程语句5 函数 二、面向对象编程1 面向对象编程基础2 类的创建及继承3 魔术方法4 多态5 设计模式 三、常用数据结构与算法1 字符串、列表、字典、集合字符串列表字典集合…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

渗透实战PortSwigger Labs指南:自定义标签XSS和SVG XSS利用
阻止除自定义标签之外的所有标签 先输入一些标签测试,说是全部标签都被禁了 除了自定义的 自定义<my-tag onmouseoveralert(xss)> <my-tag idx onfocusalert(document.cookie) tabindex1> onfocus 当元素获得焦点时(如通过点击或键盘导航&…...

CVE-2023-25194源码分析与漏洞复现(Kafka JNDI注入)
漏洞概述 漏洞名称:Apache Kafka Connect JNDI注入导致的远程代码执行漏洞 CVE编号:CVE-2023-25194 CVSS评分:8.8 影响版本:Apache Kafka 2.3.0 - 3.3.2 修复版本:≥ 3.4.0 漏洞类型:反序列化导致的远程代…...
react更新页面数据,操作页面,双向数据绑定
// 路由不是组件的直接跳转use client,useEffect,useRouter,需3个结合, use client表示客户端 use client; import { Button,Card, Space,Tag,Table,message,Input } from antd; import { useEffect,useState } from react; impor…...
智警杯备赛--excel模块
数据透视与图表制作 创建步骤 创建 1.在Excel的插入或者数据标签页下找到数据透视表的按钮 2.将数据放进“请选择单元格区域“中,点击确定 这是最终结果,但是由于环境启不了,这里用的是自己的excel,真实的环境中的excel根据实训…...

基于谷歌ADK的 智能产品推荐系统(2): 模块功能详解
在我的上一篇博客:基于谷歌ADK的 智能产品推荐系统(1): 功能简介-CSDN博客 中我们介绍了个性化购物 Agent 项目,该项目展示了一个强大的框架,旨在模拟和实现在线购物环境中的智能导购。它不仅仅是一个简单的聊天机器人,更是一个集…...
