函数序列与函数项级数
文章目录
- 函数序列与函数项级数
- 函数序列
- 函数项级数
- Weierstrass M 判别法
函数序列与函数项级数
函数序列
点态收敛:设 f n ( x ) : [ a , b ] → R f_n(x):\,[a,\,b]\to\bold{R} fn(x):[a,b]→R 是定义在区间 [ a , b ] [a,\,b] [a,b] 上的函数序列:
f 1 ( x ) , f 2 ( x ) , ⋯ , f n ( x ) , ⋯ f_1(x),\,f_2(x),\,\cdots,\,f_n(x),\,\cdots f1(x),f2(x),⋯,fn(x),⋯
若对于 ∀ α ∈ [ a , b ] \forall\,\alpha\in[a,\,b] ∀α∈[a,b] ,都有:
lim n → ∞ f n ( α ) = f ( α ) \lim\limits_{n\to\infty}f_n(\alpha)=f(\alpha) n→∞limfn(α)=f(α)
则这个函数列 { f n ( x ) } \{f_n(x)\} {fn(x)} 将点态收敛于函数:
f ( x ) : [ a , b ] → R f(x):\,[a,\,b]\to \bold{R} f(x):[a,b]→R
一致收敛:如果给定 ∀ ε \forall \varepsilon ∀ε , ∃ N ∈ N + \exists N\in N^+ ∃N∈N+ ,使得对于 ∀ n ≥ N \forall n\geq N ∀n≥N ,对于 ∀ x ∈ [ a , b ] \forall x\in [a,\,b] ∀x∈[a,b] ,都有:
∣ f ( x ) − f n ( x ) ∣ < ε \left| f(x)-f_n(x) \right|< \varepsilon ∣f(x)−fn(x)∣<ε
则称函数序列 f n ( x ) : [ a , b ] → R f_n(x):\,[a,\,b]\to\bold{R} fn(x):[a,b]→R 一致收敛于函数 f ( x ) : [ a , b ] → R f(x):\,[a,\,b]\to \bold{R} f(x):[a,b]→R ;
点态收敛和一致收敛的区别在于 ∀ x \forall x ∀x 和 ∃ N \exists N ∃N 的顺序问题:
点态收敛: ∀ x ∈ [ a , b ] , ∀ ε , ∃ N 一致收敛: ∀ ε , ∃ N , ∀ x ∈ [ a , b ] \begin{array}{l} \text{点态收敛:}\forall x\in[a,\,b],\,\forall \varepsilon,\,\exists N \\ \text{一致收敛:}\forall \varepsilon,\,\exists N,\,\forall x\in[a,\,b] \end{array} 点态收敛:∀x∈[a,b],∀ε,∃N一致收敛:∀ε,∃N,∀x∈[a,b]
因此在一致收敛的情况下,所有 [ a , b ] [a,\,b] [a,b] 中的点都有一个共同的 N N N 可以 bound,就像是 f ( x ) f(x) f(x) 周围放一个半径为 ε \varepsilon ε 的管状区域的话,那么函数 y = f n ( x ) y=f_n(x) y=fn(x) 最终都会进入这个区域里;而点态收敛的 N N N 的选择依赖于 x x x ;
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uoxLAenH-1684155322871)(figures/series_1.jpg)]
Th:设列 f n ( x ) : [ a , b ] → R f_n(x):\,[a,\,b]\to\bold{R} fn(x):[a,b]→R 是一个一致收敛于函数 f ( x ) : [ a , b ] → R f(x):\,[a,\,b]\to \bold{R} f(x):[a,b]→R 的连续函数序列,则 f ( x ) f(x) f(x) 是连续的。
证明:要证明 f ( x ) f(x) f(x) 是连续的,只需要证明 ∀ α ∈ [ a , b ] , ∀ ε > 0 \forall \alpha\in[a,\,b],\,\,\forall \varepsilon > 0 ∀α∈[a,b],∀ε>0 ,我们能够找到某个 δ > 0 \delta>0 δ>0 ,对于 0 < ∣ x − α ∣ < δ 0<|x-\alpha|<\delta 0<∣x−α∣<δ ,有:
∣ f ( x ) − f ( α ) ∣ < ε |f(x)-f(\alpha)|<\varepsilon ∣f(x)−f(α)∣<ε
对于上述 α \alpha α 、 x x x 和 ε \varepsilon ε ,由于 { f n ( x ) } \{f_n(x)\} {fn(x)} 一致收敛于 f ( x ) f(x) f(x) ,因此存在 N ∈ N + N\in N^+ N∈N+ ,使得当 n ≥ N n\geq N n≥N 时,有:
∣ f ( α ) − f n ( α ) ∣ < ε 3 ∣ f ( x ) − f n ( x ) ∣ < ε 3 \begin{align} |f(\alpha)-f_n(\alpha)| <&\, \frac{\varepsilon}{3} \\ |f(x)-f_n(x)| <&\, \frac{\varepsilon}{3} \end{align} ∣f(α)−fn(α)∣<∣f(x)−fn(x)∣<3ε3ε
而 f n ( x ) f_n(x) fn(x) 是连续的,因此对于上述 ε \varepsilon ε、 α \alpha α 和 n ≥ N n\geq N n≥N ,存在 δ > 0 \delta>0 δ>0 ,使得对于 0 < ∣ x − α ∣ < δ 0<|x-\alpha|<\delta 0<∣x−α∣<δ ,有:
∣ f n ( x ) − f n ( α ) ∣ < ε 3 |f_n(x)-f_n(\alpha)|<\frac{\varepsilon}{3} ∣fn(x)−fn(α)∣<3ε
对于上述的 δ \delta δ ,有:
∣ f ( x ) − f ( α ) ∣ = ∣ f ( x ) − f n ( x ) + f n ( x ) − f n ( α ) + f n ( α ) − f ( α ) ∣ ≤ ∣ f ( x ) − f n ( x ) ∣ + ∣ f n ( x ) − f n ( α ) ∣ + ∣ f n ( α ) − f ( α ) ∣ < ε \begin{align} |f(x)-f(\alpha)|=&\,|f(x)-f_n(x)+f_n(x)-f_n(\alpha)+f_n(\alpha)-f(\alpha)| \\ \leq &\, |f(x)-f_n(x)|+|f_n(x)-f_n(\alpha)|+|f_n(\alpha)-f(\alpha)| \\ \lt &\, \varepsilon \end{align} ∣f(x)−f(α)∣=≤<∣f(x)−fn(x)+fn(x)−fn(α)+fn(α)−f(α)∣∣f(x)−fn(x)∣+∣fn(x)−fn(α)∣+∣fn(α)−f(α)∣ε
得证。
(这个证明好经典啊,让我想到大一时复习数分的样子,当时是在二教,现在再来复习也是在二教。。。)
函数项级数
一致收敛:设 { f n ( x ) } \{f_n(x)\} {fn(x)} 是一个函数列,函数项级数:
f 1 ( x ) + f 2 ( x ) + ⋯ = ∑ k = 1 ∞ f k ( x ) f_1(x)+f_2(x)+\cdots=\sum\limits_{k=1}^{\infty}f_k(x) f1(x)+f2(x)+⋯=k=1∑∞fk(x)
一致收敛于函数 f ( x ) f(x) f(x) ,如果部分和 f 1 ( x ) f_1(x) f1(x) , f 1 ( x ) + f 2 ( x ) f_1(x)+f_2(x) f1(x)+f2(x) , f 1 ( x ) + f 2 ( x ) + f 3 ( x ) f_1(x)+f_2(x)+f_3(x) f1(x)+f2(x)+f3(x), ⋯ \cdots ⋯ 一致收敛于 f ( x ) f(x) f(x) 。用 ε \varepsilon ε 和 δ \delta δ 语言表示为对于 ∀ ε > 1 \forall \varepsilon >1 ∀ε>1, ∃ N ∈ N + \exists N\in N^+ ∃N∈N+ ,对于 ∀ n ≥ N \forall n\geq N ∀n≥N ,对于 ∀ x ∈ D \forall x\in \bold{D} ∀x∈D ,都有:
∣ f ( x ) − ∑ k = 1 n f k ( x ) ∣ < ε \left|f(x)-\sum\limits_{k=1}^nf_k(x) \right|< \varepsilon f(x)−k=1∑nfk(x) <ε
Th:如果每个函数 f k ( x ) f_k(x) fk(x) 都连续,且若 ∑ k = 1 ∞ f k ( x ) \sum\limits_{k=1}^{\infty}f_k(x) k=1∑∞fk(x) 一致收敛于 f ( x ) f(x) f(x) ,则 f ( x ) f(x) f(x) 必定连续。
证明:因为每个函数 f k ( x ) f_k(x) fk(x) 都连续,因此部分和函数 ∑ k = 1 n f k ( x ) \sum\limits_{k=1}^{n}f_k(x) k=1∑nfk(x) 都连续,由上面的定理得, f ( x ) f(x) f(x) 必定连续。
Weierstrass M 判别法
Th:设 ∑ k = 1 ∞ f k ( x ) \sum\limits_{k=1}^{\infty}f_k(x) k=1∑∞fk(x) 为函数项级数,其中没和函数 f k ( x ) f_k(x) fk(x) 都定义在实数集的子集 D \bold{D} D 上。假设 ∑ k = 1 ∞ M k \sum\limits_{k=1}^{\infty}M_k k=1∑∞Mk 是数项级数,满足:
- 0 ≤ ∣ f k ( x ) ∣ ≤ M k 0\leq |f_k(x)|\leq M_k 0≤∣fk(x)∣≤Mk 对于 ∀ x ∈ D \forall x\in \bold{D} ∀x∈D ;
- 级数 ∑ k = 1 ∞ M k \sum\limits_{k=1}^{\infty}M_k k=1∑∞Mk 收敛;
则 ∑ k = 1 ∞ f k ( x ) \sum\limits_{k=1}^{\infty}f_k(x) k=1∑∞fk(x) 绝对一致收敛。
证明:为了证明一致收敛,我们要证明对于 ∀ ε > 0 \forall \varepsilon > 0 ∀ε>0 ,我们可以找到某个 N ∈ N + N\in N^+ N∈N+ ,对于 ∀ n ≥ N \forall n\geq N ∀n≥N ,对于 ∀ x ∈ D \forall x\in \bold{D} ∀x∈D ,有:
∣ ∑ k = n ∞ f ( x ) ∣ < ε \left|\sum\limits_{k=n}^{\infty}f(x)\right| < \varepsilon k=n∑∞f(x) <ε
无论 ∑ k = 1 ∞ f k ( x ) \sum\limits_{k=1}^{\infty}f_k(x) k=1∑∞fk(x) 是否收敛,都有:
∣ ∑ k = n ∞ f ( x ) ∣ ≤ ∑ k = n ∞ ∣ f ( x ) ∣ \left|\sum\limits_{k=n}^{\infty}f(x)\right| \leq \sum\limits_{k=n}^{\infty}\left|f(x)\right| k=n∑∞f(x) ≤k=n∑∞∣f(x)∣
因为级数 ∑ k = 1 ∞ M k \sum\limits_{k=1}^{\infty}M_k k=1∑∞Mk 收敛,因此对于上述 ε \varepsilon ε ,我们可以找到某个 N ∈ N + N\in N^+ N∈N+ ,使得对于 ∀ n ≥ N \forall n\geq N ∀n≥N ,有:
∑ k = n ∞ M k < ε \sum\limits_{k=n}^{\infty}M_k < \varepsilon k=n∑∞Mk<ε
又对于 ∀ x ∈ D \forall x\in \bold{D} ∀x∈D ,有 0 ≤ ∣ f k ( x ) ∣ ≤ M k 0\leq |f_k(x)|\leq M_k 0≤∣fk(x)∣≤Mk ,故:
∣ ∑ k = n ∞ f ( x ) ∣ ≤ ∑ k = n ∞ ∣ f ( x ) ∣ ≤ ∑ k = n ∞ M k < ε \left|\sum\limits_{k=n}^{\infty}f(x)\right| \leq \sum\limits_{k=n}^{\infty}\left|f(x)\right| \leq \sum\limits_{k=n}^{\infty}M_k < \varepsilon k=n∑∞f(x) ≤k=n∑∞∣f(x)∣≤k=n∑∞Mk<ε
得证。
例:考虑级数 ∑ k = 1 ∞ x k k ! \sum\limits_{k=1}^{\infty}\frac{x^k}{k!} k=1∑∞k!xk ,我们知道它收敛于函数 e x \mathrm{e}^{x} ex ,我们使用 Weierstrass 判别法来证明这个级数在任意区间 [ − a , a ] [-a,\,a] [−a,a] 上都一致收敛。我们设 f k ( x ) = x k k ! f_k(x)=\frac{x^k}{k!} fk(x)=k!xk , M k = a k k ! M_k=\frac{a^k}{k!} Mk=k!ak ,显然对于 ∀ x ∈ [ − a , a ] \forall x\in[-a,\,a] ∀x∈[−a,a] ,有:
0 ≤ ∣ x n n ! ∣ ≤ a n n ! 0\leq \left| \frac{x^n}{n!} \right| \leq \frac{a^n}{n!} 0≤ n!xn ≤n!an
而:
lim k → ∞ M k + 1 M k = lim k → ∞ a k + 1 ( k + 1 ) ! a k k ! = lim k → ∞ a k + 1 < 1 \lim_{k\to\infty} \frac{M_{k+1}}{M_k}=\lim_{k\to\infty}\frac{\frac{a^{k+1}}{(k+1)!}}{\frac{a^k}{k!}}=\lim_{k\to\infty}\frac{a}{k+1}<1 k→∞limMkMk+1=k→∞limk!ak(k+1)!ak+1=k→∞limk+1a<1
因此级数 ∑ k = 1 ∞ M k \sum\limits_{k=1}^{\infty}M_k k=1∑∞Mk 收敛,由 Weierstrass 判别法可知 e x \mathrm{e}^x ex 的 Taylor 级数 ∑ k = 1 ∞ x k k ! \sum\limits_{k=1}^{\infty}\frac{x^k}{k!} k=1∑∞k!xk 在任意区间 [ − a , a ] [-a,\,a] [−a,a] 上都一致收敛。
相关文章:

函数序列与函数项级数
文章目录 函数序列与函数项级数函数序列函数项级数Weierstrass M 判别法 函数序列与函数项级数 函数序列 点态收敛:设 f n ( x ) : [ a , b ] → R f_n(x):\,[a,\,b]\to\bold{R} fn(x):[a,b]→R 是定义在区间 [ a , b ] [a,\,b] [a,b] 上的函数序列࿱…...
UML时序图详解
上篇文章,介绍了UML状态图,并通过visio绘制一个全自动洗衣机的UML状态图实例进行讲解。 本篇,来继续介绍UML中的另一种图——时序图。 1 时序图简介 时序图(Sequence Diagram),也叫顺序图,或序列图,是一…...

Centos7.6部署postgresql15主从
目录 安装pg15(master和standby)主数据库配置(master)初始化数据库创建归档日志目录设置数据库访问权限修改数据库配置文件开启数据库 从数据库配置(standby)同步主库的数据文件创建文件standby.signal启动从数据库 主从状态验证master上验证standby上验…...

【ThinkPHP6系列学习-2】多应用模式配置
这里写一写TP6下配置多应用。因为TP6和TP5有所差异,TP6默认是单应用模式(单模块),而我们实际项目中往往是多应用的(多个模块),所以在利用TP6是就需要进行配置,开启多应用模式。 目录…...
Linux内核oops panic简析
源码基于:Linux 5.4 0. 前言 内核异常的级别大致分为三个:BUG、oops、panic。 BUG 是指那些不符合内核的正常设计,但内核能够检测出来并且对系统运行不会产生影响的问题,比如在原子上下文中休眠,在内核中用 BUG 标识。…...

Spark大数据处理讲课笔记4.8 Spark SQL典型案例
文章目录 零、本讲学习目标一、使用Spark SQL实现词频统计(一)数据源 - words.txt(二)创建Maven项目(三)添加依赖和构建插件(四)修改源目录名称(五)创建日志属…...
WhatsApp Business 多人使用终极指南
今时今日,几乎每个人的手机上都安装了 WhatsApp,不少电商更会依赖 WhatsApp作为和客户沟通的主要渠道。但对有一定规模的店铺来说,WhatsApp绑定一个号码和设备的设定实在很不方便。如何才能用WhatsApp Business批量处理客户查询呢?…...

布局和视图的常用属性
0、用户界面由布局和GUI组件组成 之前的项目中都是使用线性布局LinearLayout,LinearLayout将视图显示在一行或一列中。其使用方法如下所示: <LinearLayoutxmlns:android"http://schemas.android.com/apk/res/android"android:layout_width…...
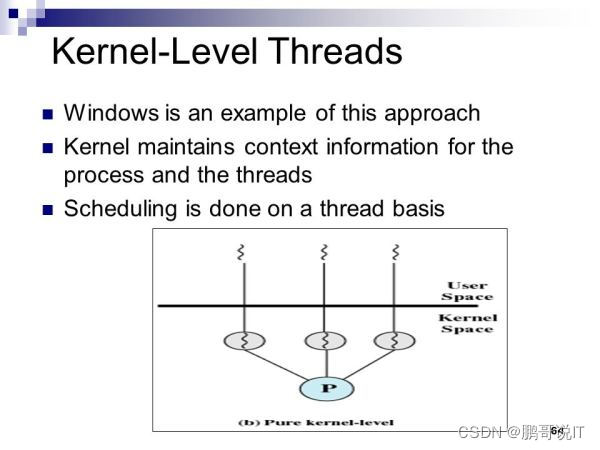
解说天下之操作系统
解说天下之操作系统 本文由桌案drawon (https://www.drawon.cn),云晶(https://www.yunjingxz.com)创始人根据多年从业经验, 从操作系统的起源,应用分类, 设计分类,以及资源使用角度对操作系统进…...
layer常用简枝(torch)方法)
Pruning 系列 (八)layer常用简枝(torch)方法
环境 python 3.9numpy 1.24.1pytorch 2.0.0+cu117一、prune.random_unstructured pytorch:文档地址 用法: torch.nn.utils.prune.random_unstructured(module, name, amount) 参数: module(torch.nn.Module) -包含要修剪的张量的模块 name(str) -module 中的参数名称,将…...
Gigabyte Z490 Vision D i9-10900k电脑 Hackintosh 黑苹果efi引导文件
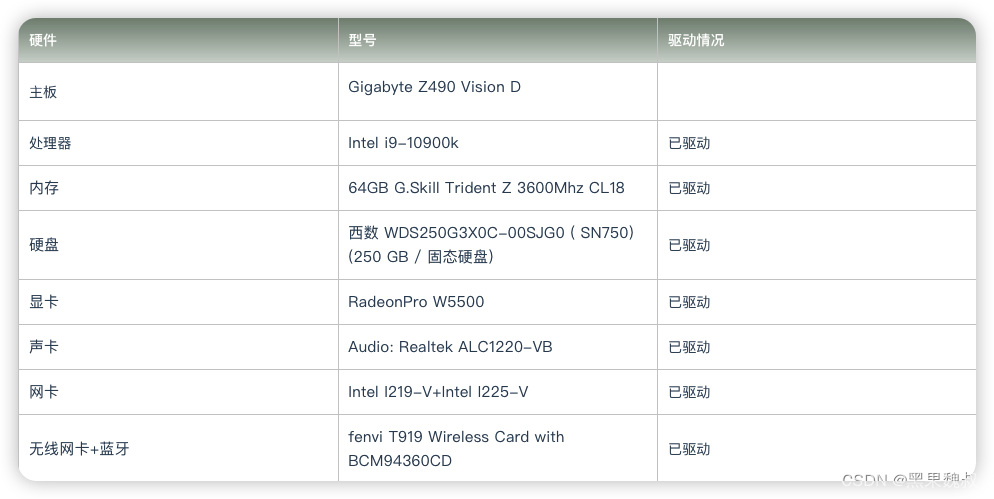
原文来源于黑果魏叔官网,转载需注明出处。(下载请直接百度黑果魏叔) 硬件型号驱动情况 主板Gigabyte Z490 Vision D 处理器Intel i9-10900k已驱动 内存64GB G.Skill Trident Z 3600Mhz CL18已驱动 硬盘西数 WDS250G3X0C-00SJG0 ( SN750) …...
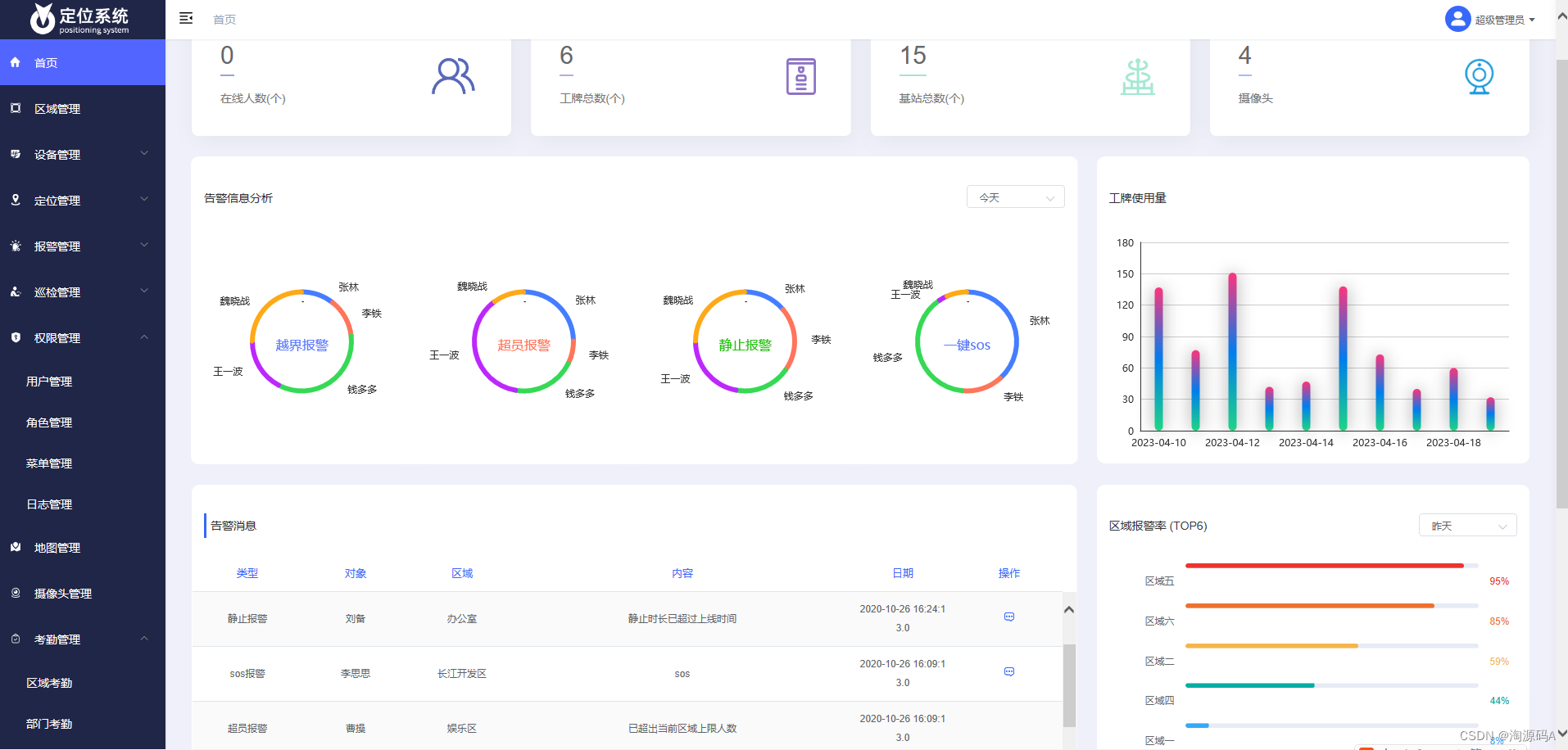
UWB智慧工厂人员定位系统源码,人员在岗监控、车辆实时轨迹监控源码
近年来人员定位系统在工业领域的发展势头迅猛,工业识别与定位成为促进制造业数字化的关键技术。通过实时定位可以判断所有的人、物、车的位置。实时定位系统要适用于复杂工业环境,单一技术是很难实现的,需要融合多种不同的定位技术࿰…...

从认识元注解到使用元注解
前言:注解是Java语言中的一种特殊语法,它可以为代码提供更加灵活的元数据信息,方便代码的处理和使用。而元注解则是用于定义注解的注解,它可以为注解提供更多的元数据信息和特性。本文将介绍如何自定义元注解,包括认识…...
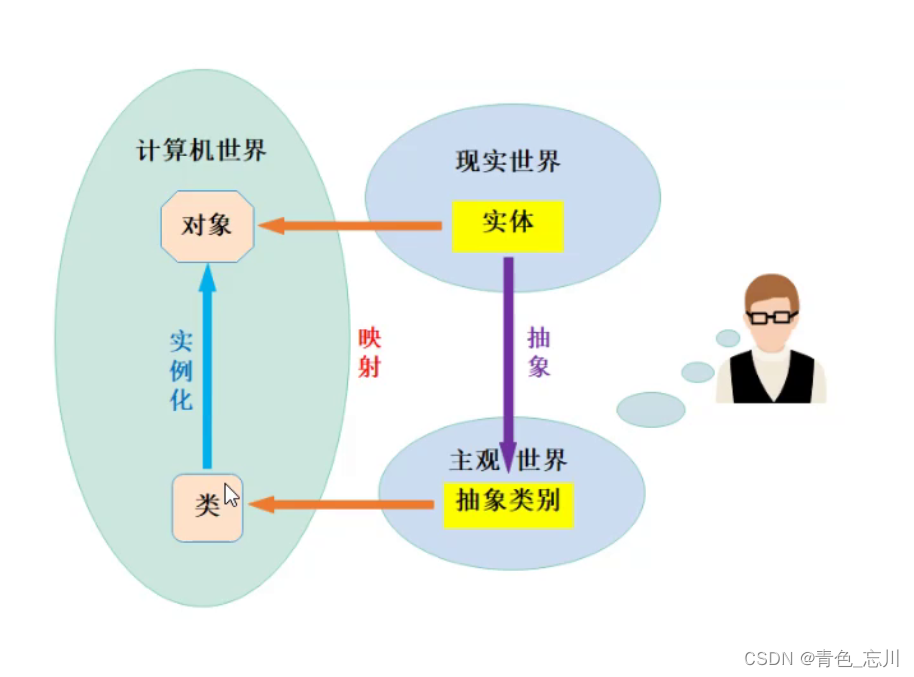
【C++从0到王者】第六站:类和对象(下)
文章目录 一、再谈构造函数1.构造函数体赋值2.初始化列表1>初始化列表的使用2>初始化列表的注意事项 3.explicit关键词 二、static成员1.如何统计当前程序中变量的个数2.static的特性3.从1加到n4.设计一个类,只能在栈或者堆上开辟空间 三、友元1.友元函数2.友…...
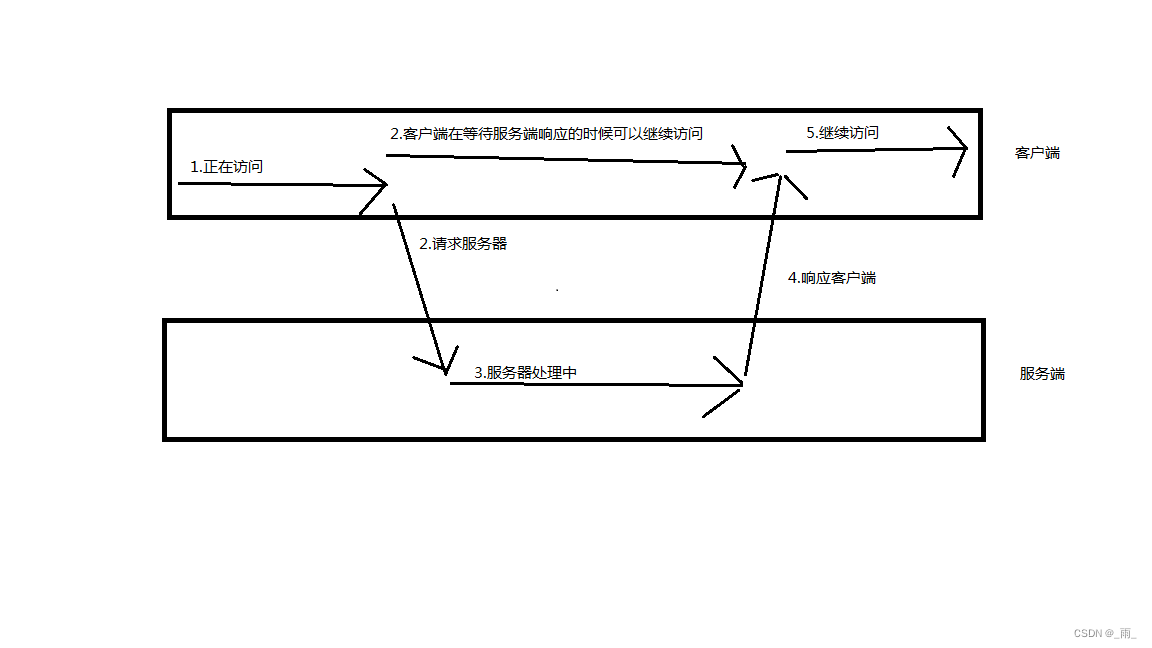
AJax和Axios的讲解
目录 Ajax Ajax基本介绍 同步异步 原生Ajax 原生的Ajax使用方式 Axios 基本介绍 Axios的基本使用 发送 get 请求 发送 post 请求 Axios快速入门 请求方法的别名 练习 Ajax Ajax基本介绍 Ajax: 全称Asynchronous JavaScript And XML,异步的JavaScript和XML…...

企业落地数字化转型,如何部署战略规划
当前环境下,各领域企业通过数字化相关的一切技术,以数据为基础、以用户为核心,创建一种新的,或对现有商业模式进行重塑就是数字化转型。这种数字化转型给企业带来的效果就像是一次重构,会对企业的业务流程、思维文化、…...
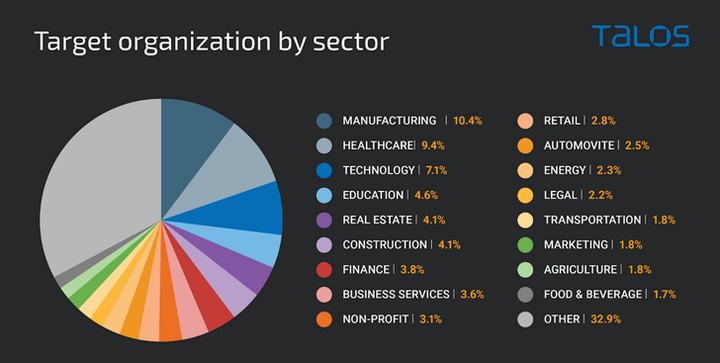
新的网络钓鱼即服务平台让网络犯罪分子生成令人信服的网络钓鱼页面
至少从2022年中期开始,网络犯罪分子就利用一个名为“伟大”的新型网络钓鱼即服务(PhaaS或PaaS)平台来攻击微软365云服务的企业用户,有效地降低了网络钓鱼攻击的门槛。 思科Talos研究员蒂亚戈佩雷拉表示:“目前,Greatness只专注于微软365钓鱼…...
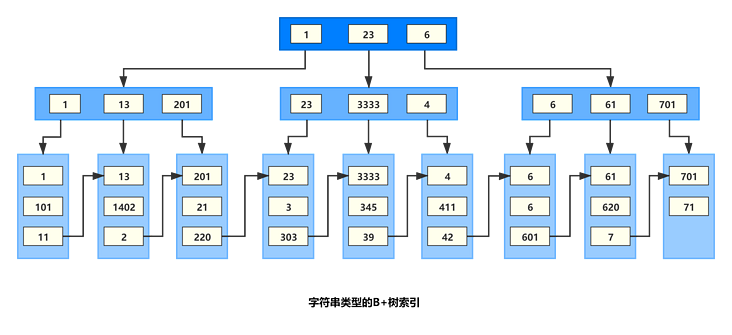
MySQL的隐式转换
隐式转换 若字符串是以数字开头,并且全部都是数字,则转换的数字结果是整个字符串;部分是数字,则转换的数字结果是截止到第一个不是数字的字符为止 若字符串不是以数字开头,则转换的数字结果是 0 varchar str "…...
LeetCode:23. 合并 K 个升序链表
23. 合并 K 个升序链表 1)题目2)过程3)代码1. 最开始2.初步优化 4)结果1. 最开始2. 初步优化 1)题目 给你一个链表数组,每个链表都已经按升序排列。 请你将所有链表合并到一个升序链表中,返回合…...
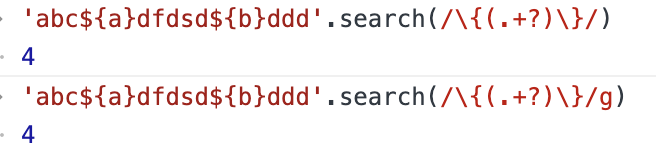
js:正则表达式常用方法总结test、exec、match、matchAll、replace、replaceAll、search
文章目录 正则使用testmatch/matchAll不加g加ggroup 的使用 matchAll不加g加g exec不加g加g searchreplace 正则使用 常用的几种方法有:test、exec、match、matchAll、replace、replaceAll、search test // 匹配返回true,不匹配false /e/.test("…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

第14节 Node.js 全局对象
JavaScript 中有一个特殊的对象,称为全局对象(Global Object),它及其所有属性都可以在程序的任何地方访问,即全局变量。 在浏览器 JavaScript 中,通常 window 是全局对象, 而 Node.js 中的全局…...
