当前位置： 首页 > news >正文

理论力学专题：张量分析

news 2026/2/9 17:20:41
  • 张量方法的引入
    • 自然法则与坐标无关，坐标系的引入方便分析，但也掩盖了物理本质
  • 指标符号
  • 哑标和自由标
    • Einstein求和约定：凡在某一项内，重复一次且仅重复一次的指标，表示对该指标在它的取值范围内求和，并称这样的指标为哑指标。
      • \begin{matrix} a_ix_i=(a_1x_1+a_2x_2+...+a_nx_n)\\ a_{ij}x_ix_j = \sum_i\sum_j a_{ij}x_ix_j \end{matrix}
    • 凡在同一项内不重复出现的指标为自由标
      • \begin{matrix} b_j = a_{ij}x_i,j=1,b_1 = a_{11}x_1 +a_{12}x_2 +a_{13}x_3 \end{matrix}
      • 同一个方程中各项自由标必须相同
      • 不能改变某一项的自由标，但所有项的自由标可以改变 
  • 克罗内克（Kronecker-δ）符号

\delta_{ij}=\left\{\begin{matrix} 1 & \,\,\,\,i=j \\ 0 & \,\,\,\,i\neq j \end{matrix}\right.

例如：ds^2=dx^2+dy^2+dz^2=dx_idx_i=\delta_{ij}dx_idx_j

常见性质：

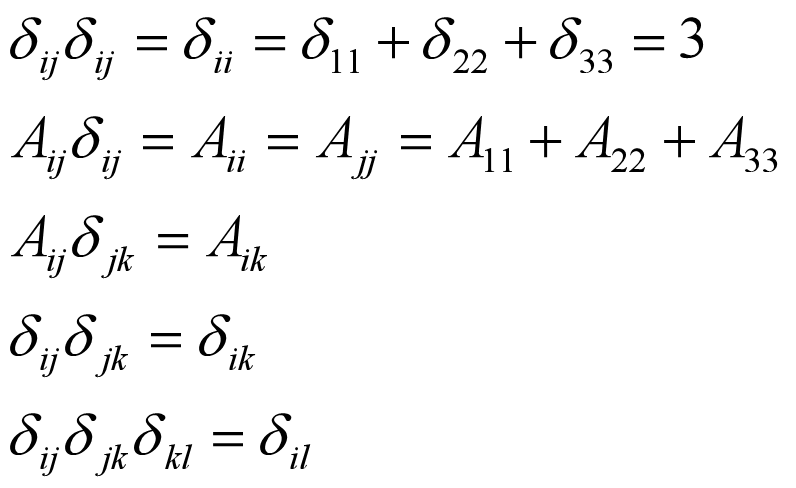
  •  Ricci 符号
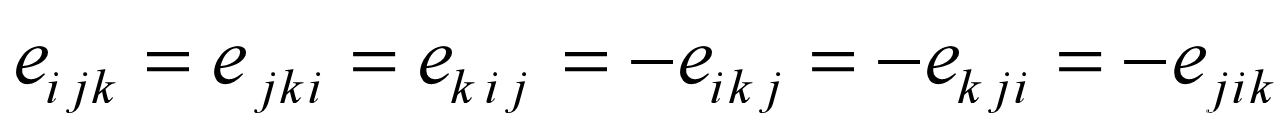
    • ｅ-δ恒等式
    • 其他重要等式

矢量的基本运算

点积

叉积

 

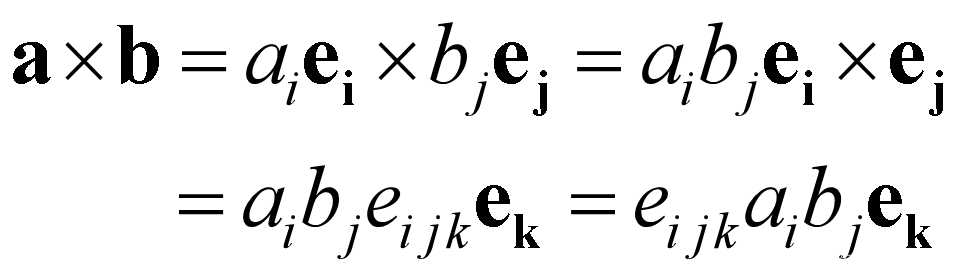
混合积

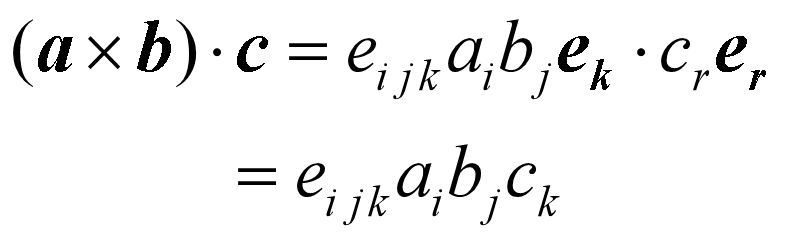
并矢

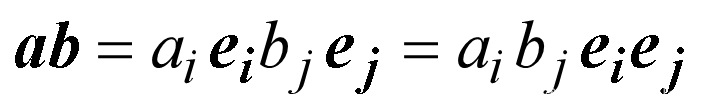
坐标变换与张量的定义 

  • 平面笛卡儿坐标系旋转变换
  • 张量定义：在坐标变换时，满足如下变换关系的量称为张量

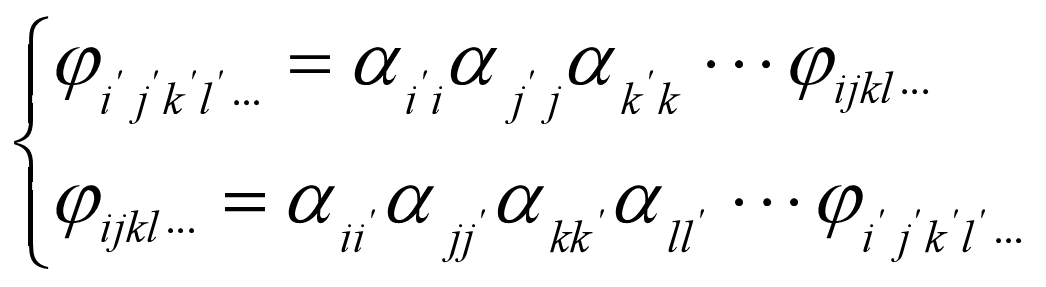
  •  可写成下式的量也称为张量

张量代数

加减法      

  • 只有同阶张量才能加减，仍为同阶张量

矢量与张量的点积

  • 点乘得到的新张量比原张量低一阶

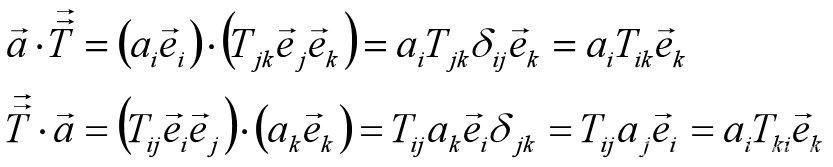
矢量与张量的叉积

  • 叉乘得到的新张量与原张量同阶

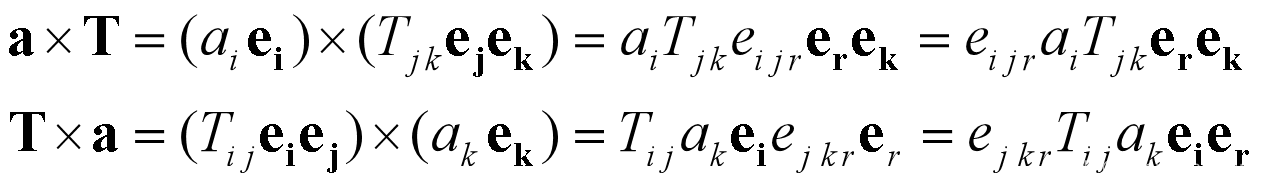
张量与张量的点积

  • 两个张量点积的结果仍为张量。新张量的阶数是原两个张量的阶数之和减2。

张量的双点积

张量的双叉乘

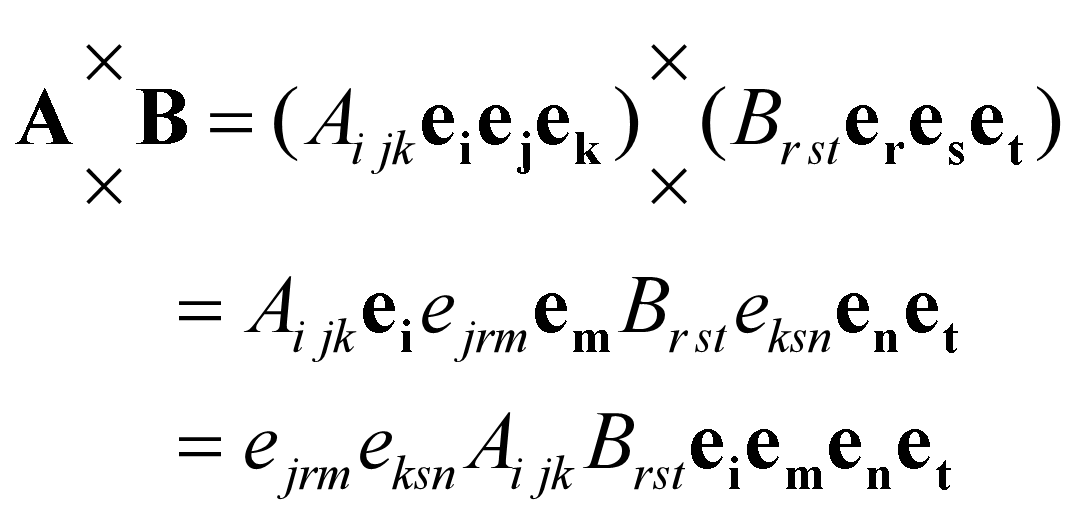
张量缩并

  • 进行缩并：将其中的二个基矢量点乘，得到比原张量低二阶的新张量。二阶张量相当于将对角元素求和。
  • 张量代数的商法则是指当两个张量空间之间的同态映射存在时，我们可以定义一个商空间，并在该空间中定义一个张量积。这种定义允许我们通过将一个张量空间中的元素等价于另一个张量空间中的元素，来将一个张量空间划分成等价类。在商空间中，我们将两个商元素的张量积定义为它们代表的等价类中的两个未经缩并的张量的张量积的等价类。这样，我们可以通过定义商张量空间来处理彼此之间有联系的张量空间。

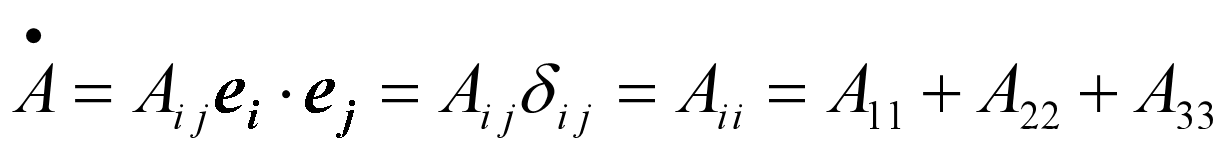
指标置换

  • 若对该张量的分量中任意两个指标交换次序，得到一个与原张量同阶的新张量。

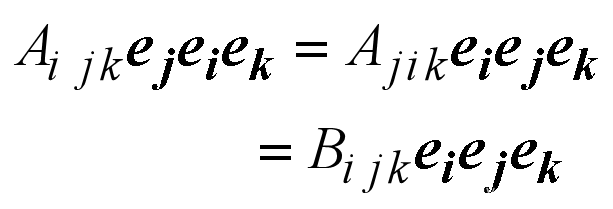
对称化和反称化

  • 对于二阶张量：
    • 对称，有6个独立分量
    • 反对称，有3个独立分量

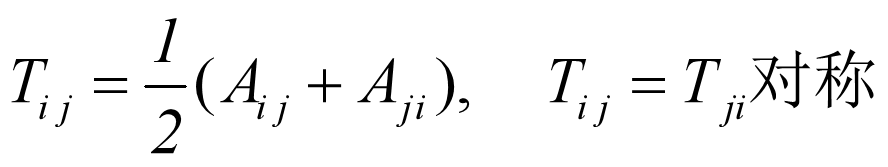
  • 高阶张量：
    • 关于（指标，指标）对称的？阶张量/反对称张量

商法则

  • 张量代数的商法则是指当两个张量空间之间的同态映射存在时，我们可以定义一个商空间，并在该空间中定义一个张量积。这种定义允许我们通过将一个张量空间中的元素等价于另一个张量空间中的元素，来将一个张量空间划分成等价类。在商空间中，我们将两个商元素的张量积定义为它们代表的等价类中的两个未经缩并的张量的张量积的等价类。这样，我们可以通过定义商张量空间来处理彼此之间有联系的张量空间。

二阶张量（仿射量）

  • 二阶张量相当于一个方矩阵，在向量空间有类似线性变换算子的作用。
    • 是线性算子

转置

略

逆

略

对称仿射量的主向和主值

  •  对于仿射量B，若存在三个相互垂直的方向i,j,k,其映象 B\cdot i,B\cdot j,B\cdotｋ也相互垂直，则称该三个方向为B的主向。
  • 对称仿射量T必存在三个主向和三个相应的主值。
  • 主值S满足特征方程：
    • 其中，Ⅰ，Ⅱ，Ⅲ称为仿射量T的第一、第二、第三不变量

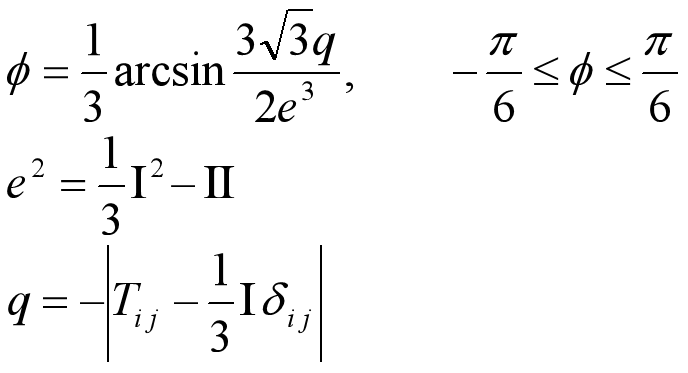各向同性张量 

  • 在坐标任意变换时，各分量保持不变的张量，称为各向同性张量。 
    • 零阶张量(标量)总是各向同性的。
    • 一阶张量(矢量)总不是各向同性的。
    • 对称二阶张量其三个主值相等与其各向同性等价。

 

张量分析

梯度、散度、旋度

  • Hamilton算子
    • Hamilton算子相当于一阶张量

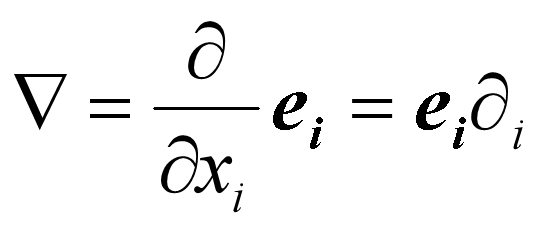
容许变换

  • 容许变换被用来表示在不同坐标系下的张量，而不是在一个特定的坐标系中。这在应用中非常有用，因为在不同坐标系中对于同一个物理问题的描述是常见的。通过使用容许变换，张量可以在不同的坐标系中转换，以便分析和处理。
  • 在计算机图形学中，容许变换常用于表示三维物体在不同的观察角度下的变化。这种类型的变换可以通过一个矩阵来实现，称为旋转矩阵。旋转矩阵可以用来描述平面和立体图形的旋转、缩放和平移。
  • 如下，依次有坐标变换和逆变换

  •  满足以下两个条件的变换称之为容许变换
    • 正逆变换函数均为单值连续可微函数
    • 在域内任意点处：

     

度规张量

  • 度规张量是描述空间度量的数学工具，在张量分析中非常重要。度规张量可以用来表示空间的内部结构和变形情况，也可以用来计算曲率、变形等量。
  • 在三维欧几里得空间中，度规张量可以表示为一个对称的二阶张量。它的每一个分量对应于两个向量之间的夹角余弦值，因此可以用来测量向量之间的角度和长度。
  • 度规张量还可以用来描述时空的性质。在相对论中，时空被视为四维弯曲的，度规张量可以用来描述这种弯曲的情况，进而推导出广义相对论的基本公式和方程。

 （度量张量，仅当i=j成立）

 例如：球坐标系

g_{ij}=\begin{bmatrix} 1 &\,\,0 &\,\,0 \\ 0 &\,\,r^2 &\,\, 0 \\ 0 & \,\,0 &\,\,r^2sin^2\theta \end{bmatrix}

矩阵导数

  • 常数求导为常数零
  • 线性算子
  • 乘积法则

 

  • 商法则

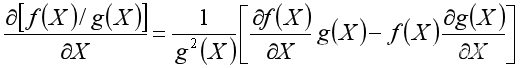
  • 经验式1

 

  • 经验式2

 

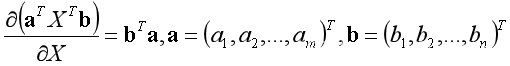
  • 经验式3

  • 经验式4

 

相关文章：

理论力学专题：张量分析

张量方法的引入 自然法则与坐标无关，坐标系的引入方便分析，但也掩盖了物理本质指标符号哑标和自由标 Einstein求和约定：凡在某一项内，重复一次且仅重复一次的指标，表示对该指标在它的取值范围内求和，并称这…...

编程日记 2023/5/29 23:33:12

索引失效情况

左或者左右模糊匹配，like %xx，like %xx% select * from student where name like %三; 原因：B是按照索引值有序排列，只能根据前缀比较来确定数据，一旦左边是模糊的，显然无法确定到底是哪个索引值 对索引字…...

编程日记 2023/5/19 17:30:50

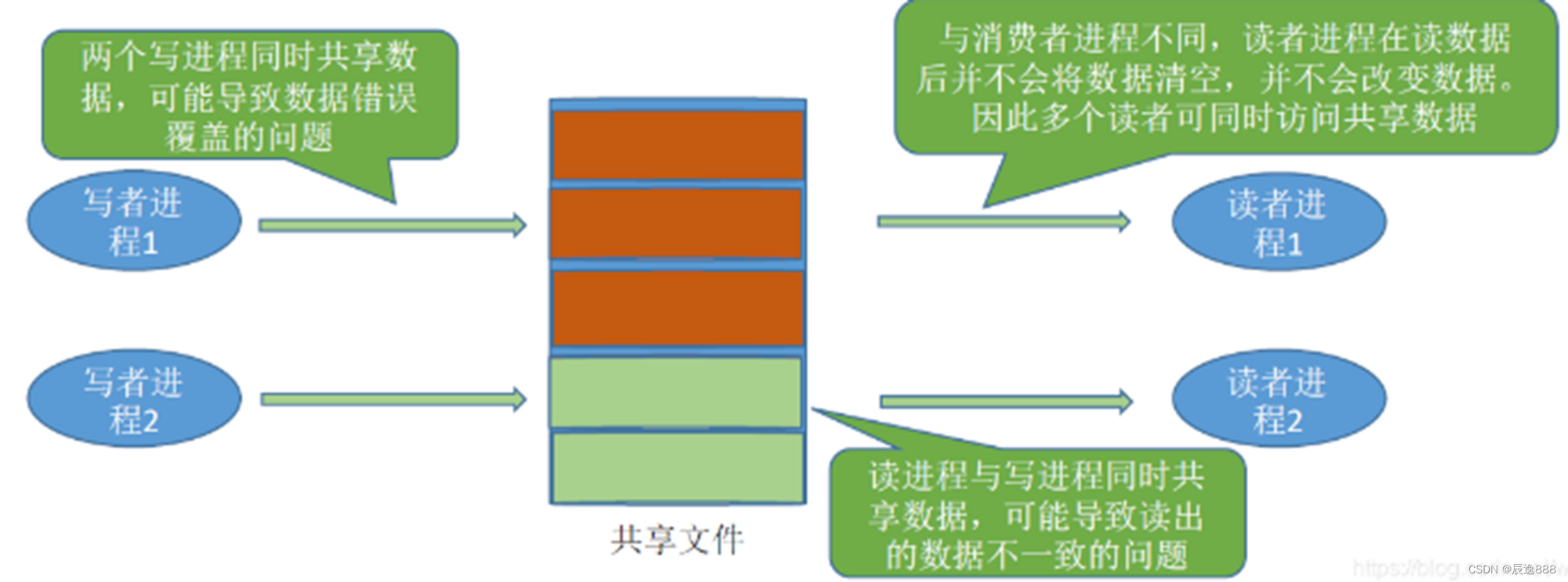
pv操作练习题

信号量解决五个哲学家吃通心面问题 题型一 有五个哲学家围坐在一圆桌旁，桌中央有盘通心面，每人面前有一只空盘于，每两人之间放一把叉子。每个哲学家思考、饥饿、然后吃通心面。为了吃面，每个哲学家必须获得两把叉子，…...

编程日记 2023/5/19 17:25:48

【小菜鸡刷题记】--字符串篇

【小菜鸡刷题记】：字符串 剑指 Offer 05. 替换空格剑指 Offer 58 - II.左旋转字符串剑指 Offer 20.表示数值的字符串剑指 Offer 67. 把字符串转换成整数 特此声明：题目均来自于力扣 剑指 Offer 05. 替换空格 题目链接 请实现一个函数，把字符…...

编程日记 2023/5/19 17:20:47

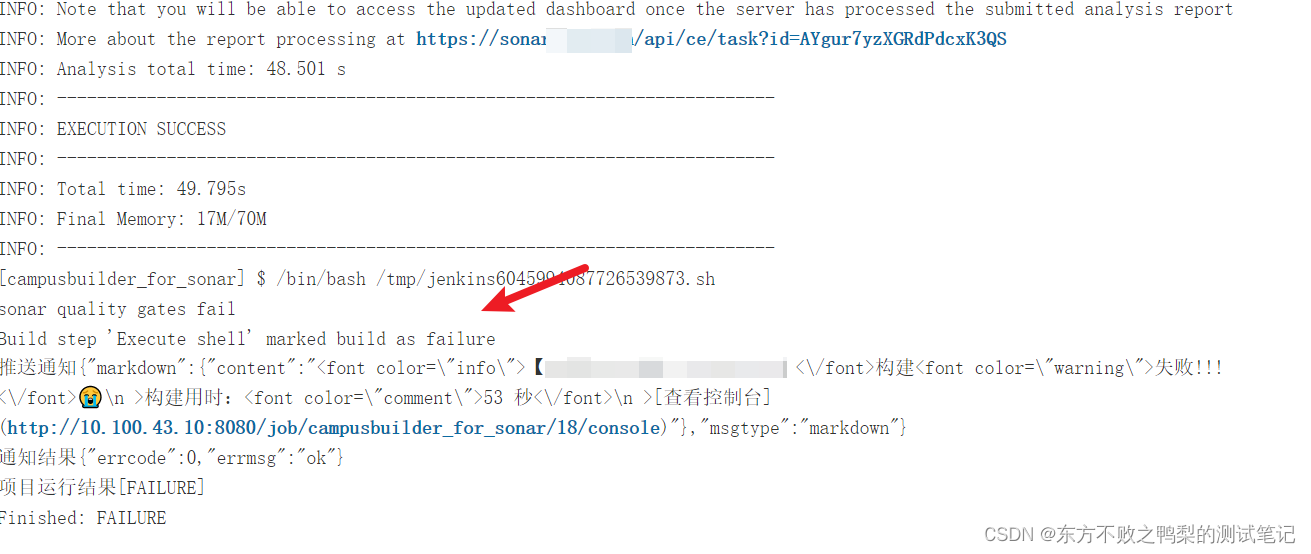
Sonar加入jenkins流水线

前提：已搭建sonarqube 1、配置sonarqube server jenkins 中manage jenkins-configure System配置sonarqube server 2、准备sonar环境 在jenkins项目的构建环境步骤中，勾选prepare SonarQube environment token需要提前在凭据里添加一个token 3、执行s…...

编程日记 2023/5/19 17:15:46

FSW26现金回收RS FSW43 信号和频谱分析仪

Rohde & Schwarz FSW26信号和频谱分析仪，2 Hz - 26.5 GHz 高性能 Rohde & Schwarz (R&S) FSW26 信号和频谱分析仪专为方便、准确和快速而设计。其独特的触摸屏、直观的多视图结果显示和优化的用户指南使 R&S FSW26 分析仪的操作高效方便。凭借其无…...

编程日记 2023/5/30 20:48:24

GraphPad Prism 9.5.1 for Mac 操作简便功能强大且实用的医学绘图分析工具

GraphPad Prism简介 GraphPad Prism是一款非常实用的统计软件，其功能非常强大，能够帮助用户进行各类科研数据的处理和分析，快速绘制出各种专业的图像和数据报告。 GraphPad Prism软件的用户界面非常友好，易于学习和操作&#xf…...

编程日记 2023/5/19 17:05:42

六. Activity启动模式

Task任务栈(ActivityTask) Activity属于App进程,但是Task属于操作系统,Task里面的Activity可以是属于不同的App的,所以App之间是可以相互调用的.比如:App里面可以使用打电话、地图等. 当我们查看手机后台运行的程序,他们其实就是一个个任务栈Task,我们平时可能会把他认为是一个…...

编程日记 2023/5/19 17:00:40

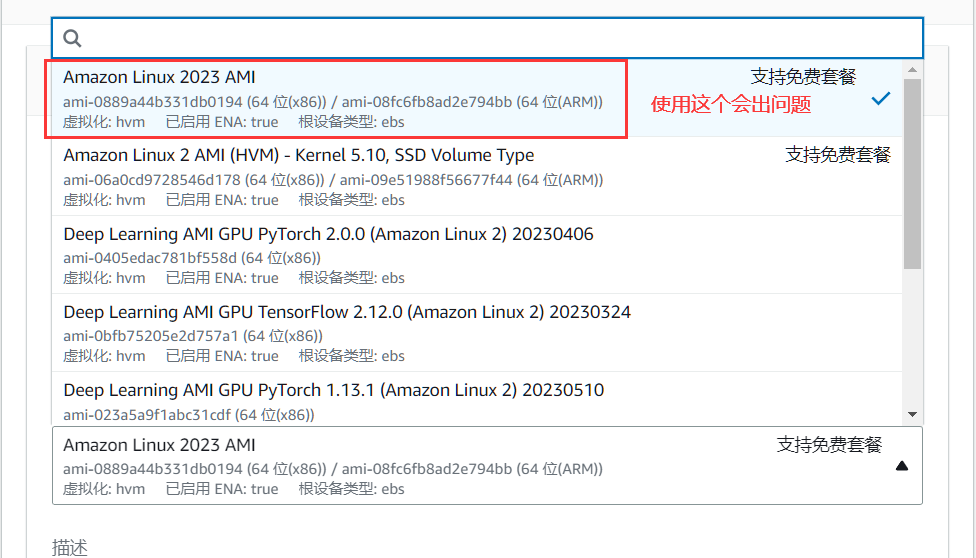
本机连接aws的ec2时报错：所选用户的用户密钥未在远程主机上注册

引言 由于工作的需要，所以需要去学习下AWS相关的知识，所以自己注册了一个AWS的账号去进行学习。 问题发现 按照启动ec2实例的步骤：选择镜像->选择系统配置->配置密钥对->配置安全组->设置存储卷大小->启动实例 在上述操作…...

编程日记 2023/5/19 16:55:38

谁看见我的猫照片了

今天分享一个可自由拖得动的图片效果样式。 先看效果&#xff1a; 谁看见我猫的照片了&#xff1f; 再上源码&#xff1a; <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Title</title><st…...

编程日记 2023/5/19 16:50:37

数据结构与算法之深度优先算法详解

深度优先算法&#xff08;Depth First Search&#xff0c;DFS&#xff09;是一种常见的图形算法&#xff0c;它是一种用于遍历或搜索树或图的算法。在深度优先搜索中&#xff0c;我们首先探索一个子树的深度&#xff0c;然后再回溯到父节点&#xff0c;接着探索另一个子树的深度…...

编程日记 2023/5/30 20:48:41

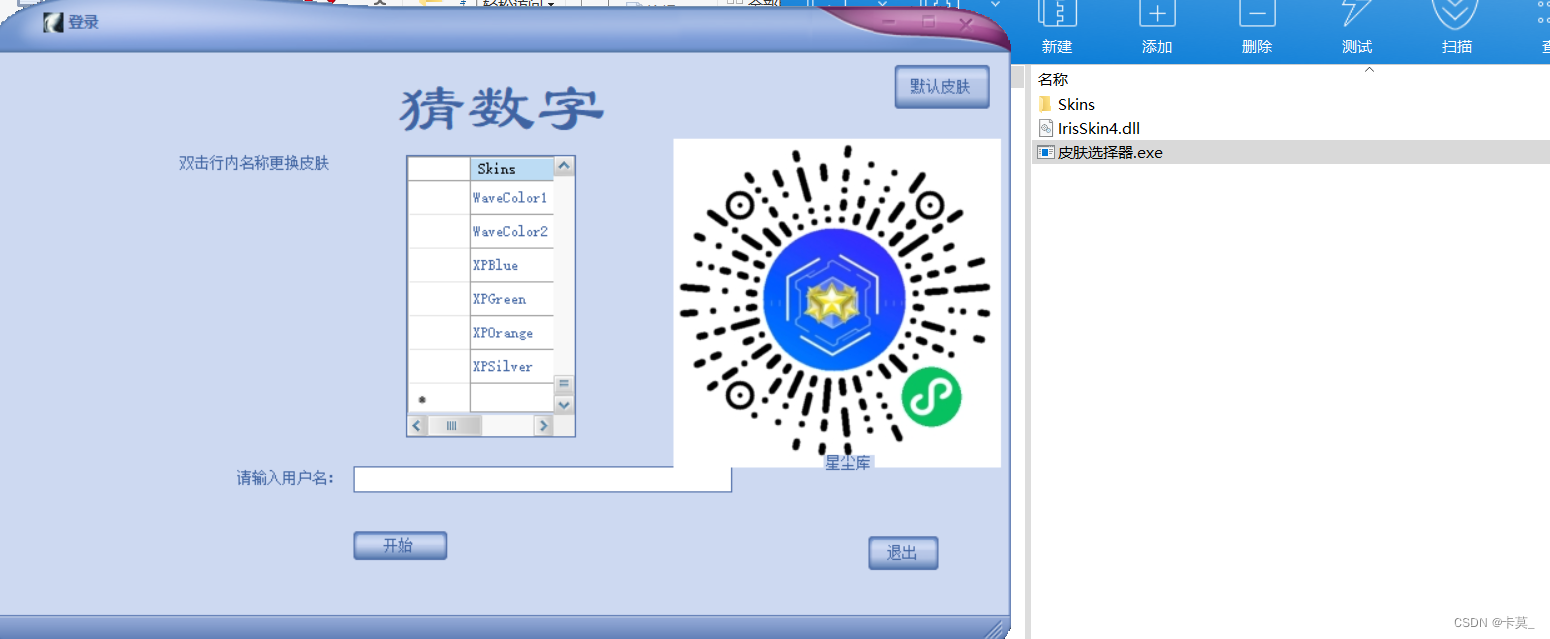
C# 给winfrom窗体添加皮肤控件

如何快速给C# winform添加好看的皮肤C# Winform中窗体的美化 SkinEngine的应用 皮肤控件换肤素材包&#xff0c;IrisSkin2.dll皮肤素材资源下载 压缩包内一共有22种皮肤素材&#xff0c;使用说明&#xff1a;把控件拖到你的form上&#xff0c;只需一行代码&#xff0c;即可实…...

编程日记 2023/5/19 16:40:35

数据分析真的很火吗？真的有很多企业需要这样的岗位吗？求大佬指点。

“我是去年毕业的&#xff0c;因为疫情影响&#xff0c;整个就业环境都很不好&#xff0c;很多企业都裁员了。加上疫情三年基本都是玩过去&#xff0c;也没啥一技之长&#xff0c;就业就更难了。听说现在做数据分析的人很多&#xff0c;我身边的朋友都在转行做数据分析。 其实…...

编程日记 2023/5/19 16:35:33

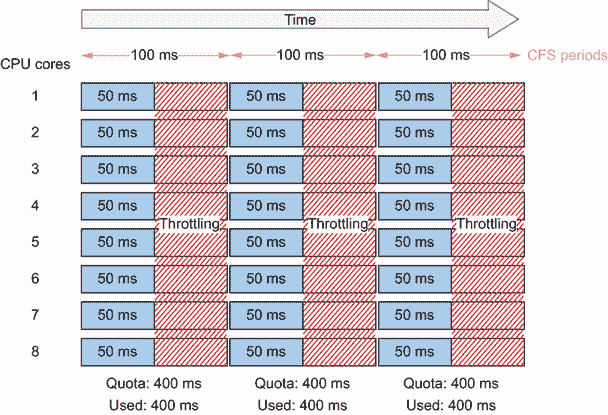
100 个 Go 错误以及如何避免：9~12

协议&#xff1a;CC BY-NC-SA 4.0 译者&#xff1a;飞龙 本文来自【OpenDocCN 饱和式翻译计划】&#xff0c;采用译后编辑&#xff08;MTPE&#xff09;流程来尽可能提升效率。 真相一旦入眼&#xff0c;你就再也无法视而不见。——《黑客帝国》 九、并发实践 本章涵盖 防止 …...

编程日记 2023/5/19 16:30:30

用户/用户组管理

用户管理 * useradd 命令添加用户&#xff0c;会在/etc/passwd生成用户信息&#xff0c;信息分为7列&#xff0c;被6个冒号隔开 第一列 username (login name) 第二列 密码&#xff0c;但是该列已经被移除&#xff0c;用x表示&#xff0c;密码信息已经存放在了/etc/shadow文…...

编程日记 2023/5/19 16:25:29

如何进行TCP抓包调试？

网络调试工具——Wireshark Wireshark 是世界上应用最广泛的网络协议分析器&#xff0c;它让我们在微观层面上看到整个网络正在发生的事情。 Wireshark 本身是一个开源项目&#xff0c;所以也得到了很多志愿者的支持。同时&#xff0c;Wireshark 具有丰富的功能集&#xff0c;…...

编程日记 2023/5/19 16:20:28

分享一个国内可用的ChatGPT网站，免费无限制，支持AI绘画 - AI 百晓生

背景 ChatGPT作为一种基于人工智能技术的自然语言处理工具&#xff0c;近期的热度直接沸腾&#x1f30b;。 作为一个AI爱好者&#xff0c;翻遍了各大基于ChatGPT的网站&#xff0c;终于找到一个免费&#xff01;免登陆&#xff01;手机电脑通用&#xff01;国内可直接对话的C…...

编程日记 2023/5/19 16:15:27

API安全性的要素与开发人员必修课测试

一、API安全性的要素主要包括以下几点&#xff1a; 1.身份验证和访问控制&#xff1a;API应该通过身份验证来验证请求的源&#xff0c;确保只有授权的用户或应用程序才能访问API。这可以通过使用API密钥、访问令牌、OAuth令牌或其他身份验证机制实现。 2.数据加密&#xff1a;A…...

编程日记 2023/5/19 16:10:25

leetcode 651. 4键键盘

651. 4键键盘 中等 102 company 微软 Microsoft company 谷歌 Google company 亚马逊 假设你有一个特殊的键盘包含下面的按键&#xff1a; A&#xff1a;在屏幕上打印一个 ‘A’。Ctrl-A&#xff1a;选中整个屏幕。Ctrl-C&#xff1a;复制选中区域到缓冲区。Ctrl-V&#xff1a…...

编程日记 2023/5/19 16:05:25

Python垃圾回收机制

Python 运行过程中会不停的创建各种变量&#xff0c;而这些变量是需要存储在内存中的&#xff0c;随着程序的不断运行&#xff0c;变量数量越来越多&#xff0c;所占用的空间势必越来越大&#xff0c;如果对变量所占用的内存空间管理不当的话&#xff0c;那么肯定会出现 out of…...

编程日记 2023/5/19 16:00:24

智慧医疗能源事业线深度画像分析（上）

引言 医疗行业作为现代社会的关键基础设施，其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入，智慧医疗能源事业线应运而生，致力于通过创新技术与管理方案，重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

编程新知 2026/2/8 20:41:46

【WiFi帧结构】

文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成&#xff1a;MAC头部frame bodyFCS&#xff0c;其中MAC是固定格式的&#xff0c;frame body是可变长度。 MAC头部有frame control&#xff0c;duration&#xff0c;address1&#xff0c;address2&#xff0c;addre…...

编程新知 2026/2/7 17:33:19

SciencePlots——绘制论文中的图片

文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了&#xff1a;一行…...

编程新知 2025/9/8 13:50:07

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例

使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件&#xff0c;常用于在两个集合之间进行数据转移&#xff0c;如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model&#xff1a;绑定右侧列表的值&…...

编程新知 2026/2/4 4:25:40

Cesium1.95中高性能加载1500个点

一、基本方式&#xff1a; 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

编程新知 2025/12/17 2:10:10

PAN/FPN

import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

编程新知 2025/10/20 4:39:36

C++：多态机制详解

目录 一. 多态的概念 1.静态多态&#xff08;编译时多态&#xff09; 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1&#xff09;.协变 2&#xff09;.析构函数的重写 5.override 和 final关键字 1&#…...

编程新知 2026/1/25 13:32:52

【网络安全】开源系统getshell漏洞挖掘

审计过程&#xff1a; 在入口文件admin/index.php中&#xff1a; 用户可以通过m,c,a等参数控制加载的文件和方法&#xff0c;在app/system/entrance.php中存在重点代码&#xff1a; 当M_TYPE system并且M_MODULE include时&#xff0c;会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

编程新知 2026/1/31 2:59:25

基于Java+VUE+MariaDB实现（Web）仿小米商城

仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意&#xff1a;运行前…...

编程新知 2026/1/31 4:37:40

探索Selenium：自动化测试的神奇钥匙

目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

编程新知 2025/11/19 18:06:51