MSQL系列(一) Mysql实战-索引结构 二叉树/平衡二叉树/红黑树/BTree/B+Tree
Mysql实战-索引结构 二叉树/平衡二叉树/红黑树/BTree/B+Tree
我们在项目中都会使用索引,所以我们要了解索引的存储结构,今天我们就着重讲解下Mysql的索引结构存储模型,并且看下 二叉树,平衡二叉树,红黑树,BTree及B+Tree的演变过程
1.索引的组成
为什么会有索引?
为了方便我们查找数据,快捷的查找数据,就像目录一样,我们在翻书的时候,可以根据目录,直接找到相应的位置,在DB中,索引就是在读取的数据的过程中,查找数据的目录信息
什么是联合索引?
联合索引就是多个字段的索引, 为什么需要联合索引呢? 下面我们看一个例子
user 表结构如下
CREATE TABLE `user` (`id` bigint NOT NULL AUTO_INCREMENT COMMENT '主键',`id_card` char(32) CHARACTER SET utf8mb4 COLLATE utf8mb4_unicode_ci NOT NULL COMMENT '身份证ID',`user_name` char(32) CHARACTER SET utf8mb4 COLLATE utf8mb4_unicode_ci NOT NULL COMMENT '用户名字',`age` int NOT NULL COMMENT '年龄',PRIMARY KEY (`id`)
) ENGINE=InnoDB AUTO_INCREMENT=1 DEFAULT CHARSET=utf8mb4 COLLATE=utf8mb4_unicode_ci COMMENT='用户表'> OK
> 时间: 0.627s
如果我们需要查询 身份证号 和 姓名信息, 我们应该如何操作?
select user_name from user where id_card = "xxxxx"
这个查询语句意味着什么? 回表查询
为什么会发生回表?这就要探究下我们的索引结构了,怎么能避免回表
2.索引结构
什么是回表查询 ? 讲清楚 回表查询之前,我们必须清楚的知道 Mysql的索引存储结构,这样才能讲明白回表查询
大家都知道Mysql 采用B+Tree 来存储索引结构,那么你一定听说过BTree, 那么他们俩到底有什么区别呢?
- Btree 是为了磁盘或其他存储设备而设计的一种多叉平衡树
- Btree 相当于二叉树,Btree每个内节点有多个分支,即多叉
- B+Tree是BTree的一个变种,是BTree在数据库中的一个实现,是常见的也是数据库中使用最为频繁的一种索引
2.1 二叉树,二叉平衡树
二叉树是什么?
这是二叉树大致的情况
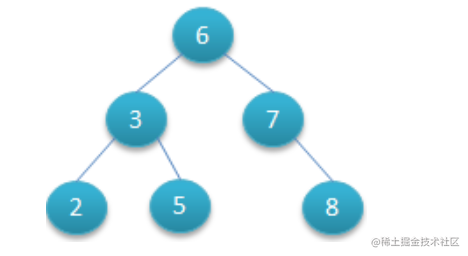
二叉树的极端情况-单链到底
二叉树 存在一种极端的情况, 这种效率就很差,一条链路走到底,效率极为低下
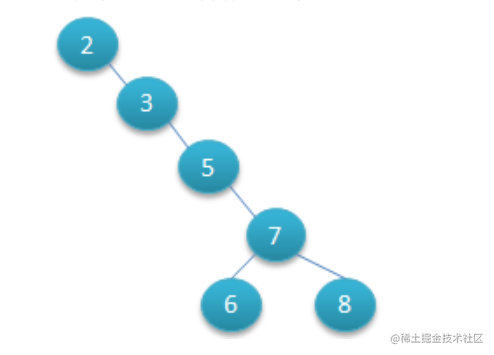
二叉平衡树
为了解决 一条路走到底的问题, 印出来了二叉平衡树,平衡二叉树 (AVL) 树是一种自平衡二叉查找树 (BST),
- 平衡二叉树是二叉树对于空间密度提升的升级
- 平衡二叉树比二叉树比较有规则,所以深度比二叉树小
- 所有节点的左右子树的高度差不能超过 1
- 平衡二叉树在数据量大的时候查询和插入速度都大于二叉树
2.2 红黑树
那什么是红黑树呢? 其实红黑树和上面的平衡二叉树类似, 红黑树是一种自平衡二叉搜索树
- 红黑树 每个节点多了一个额外的位置用来存储节点的颜色(红色或黑色)
- 每个节点颜色只有红或黑,要么是红色,要么是黑色,唯一选择
- 红黑树的根节点一定是黑色的
- 红黑树所有的叶子节点全是null,黑色
- 红黑树不能有相邻的红色节点,即红色节点不能有父/子 红节点
- 从任一节点到子树的每个叶子节点黑色节点数相同 叫做节点的黑高
- 从根节点到每个叶子节点路径的黑色节点数相同 叫做树的黑高
上面这些限制就是为了 红黑树实现自平衡而定义的准则,有了这些准则,就能避免 二叉树极端情况成为单链的场景,最后两点比较难理解,我们来验证下
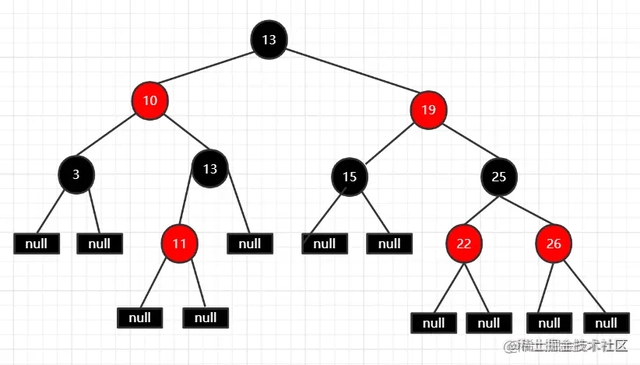
- 从任一节点到子树的每个叶子节点黑色节点数相同 叫做节点的黑高
- 计算节点黑高
- 根13->叶子A, 13->3->null 节点黑高3
- 根13->叶子B,13->19->25->26->null, 黑色节点 13,25,null 节点黑高3
- 所以从任一节点到叶子节点 黑节点数相同,黑高
- 从根节点到每个叶子节点路径的黑色节点数相同 叫做树的黑高
- 根节点 13,到叶子A, 3个黑色节点, 树的黑高就是3
- 黑高为3的红黑树,最小高度是3,全黑
- 黑高为3的红黑树,最大高度是5,交替红黑
- 黑稿为3的红黑树,子树最小高度是2,最大高度为4
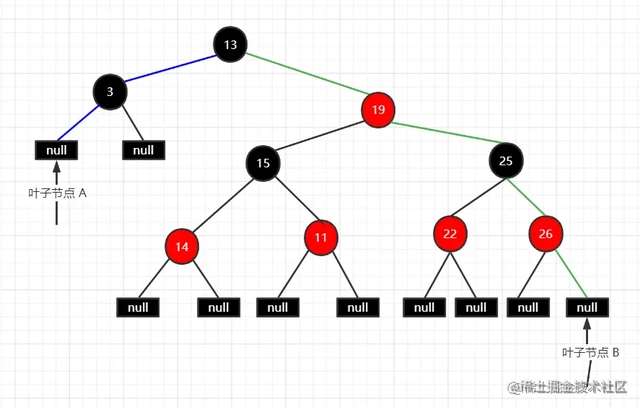
红黑树有什么操作呢?
红黑树的基本操作和其他树形结构一样,一般都包括查找、插入、删除等操作。
- 查找 红黑树是二叉树的一种,查找过程和二叉查找树一样
- 插入 红黑树的插入很复杂,红黑树插入新节点后,需要进行调整,新插入的新节点一定是红色
- 如果插入的节点是黑色,那么这个节点所在路径比其他路径多出一个黑色节点,这个调整起来会比较麻烦。
- 如果插入的节点是红色,此时所有路径上的黑色节点数量不变,仅可能会出现两个连续的红色节点的情况,这种情况下,通过变色和旋转进行调整即可
- 删除 删除更为复杂,要确定待删除节点有几个孩子,还要找删除节点的前驱/后继节点等等,不做赘述
2.3 B-Tree就叫做BTree
不存在B减树, 要么是BTree 要么是B+Tree,不存在B减树这种叫法,B树是一种多路自平衡搜索树,它类似普通的二叉树,但是BTree 允许每个节点有更多的子节点,这是和二叉树最大的区别, 每个子节点存在多节点
下面我们来看下BTree的特点 以下以下
- 所有键值分布在整个树中
- 任何关键字出现且只出现在一个节点中
- 搜索有可能在非叶子节点结束
- 在关键字全集内做一次查找,性能近似于二分查找算法
BTree 的数据存在每个节点中,所以每个节点能够保存的索引值很少,所以存储大量数据时,树的层级会很高,这样就导致与磁盘的 IO 交互次数增多,查找数据的效率就变得很低,为什么这么说?
我们来模拟一下BTree查找过程
可以看到有磁盘块和P1/P2/P3指针信息, 比如我现在要查找 60 60元素存储在 磁盘块9 中
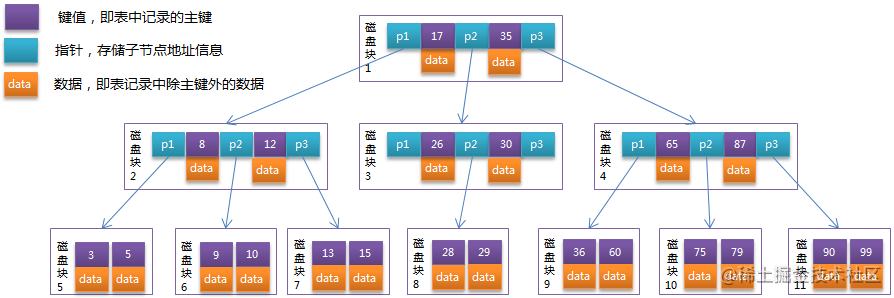
- 第一步 找 60 , 先根据根节点信息,找到根节点存储的磁盘1 ,把磁盘1信息加载到内存 发生磁盘IO操作第1次
- 第二步 加载磁盘1后,内存中有两个文件17和35及3个记录其他磁盘的地址的指针数据P1/P2/P3,根据 60 >35 ,因此我们二叉树右子树查找,找到指针 P3
- 第三步 根据P3指针,定位磁盘4, 然后把磁盘4的信息加载到内存,发生磁盘IO操作第2次
- 第四步 加载磁盘4后,内存中有两个文件 65和87及3个记录其他磁盘的地址的指针数据P1/P2/P3,根据 60 < 65 ,因此我们找二叉树左子树查找,找到指针 P1
- 第五步 根据指针P1, 定位磁盘9, 然后把磁盘9的信息加载到内存,发生磁盘IO操作第3次
- 第六步 加载磁盘9后,内存中有两个文件 36和60, 对比 要找的元素 60,找到,并且定位了该文件所在的磁盘位置 磁盘9
该过程 发生了三次IO过程,从磁盘加载了3次数据信息, 频繁的从IO磁盘获取数据, 这就产生了B+Tree,下一篇文章,我们介绍下B+Tree
本文 我们介绍了索引的基本结构,包括二叉树,平衡二叉树,红黑树,BTree的演变过程和他们之间的区别,特别是红黑树,插入和删除都需要复杂的操作,也讲解了BTree的读取原理,继而引出B+Tree与之对比
相关文章:

MSQL系列(一) Mysql实战-索引结构 二叉树/平衡二叉树/红黑树/BTree/B+Tree
Mysql实战-索引结构 二叉树/平衡二叉树/红黑树/BTree/BTree 我们在项目中都会使用索引,所以我们要了解索引的存储结构,今天我们就着重讲解下Mysql的索引结构存储模型,并且看下 二叉树,平衡二叉树,红黑树,B…...

理论力学专题:张量分析
张量方法的引入 自然法则与坐标无关,坐标系的引入方便分析,但也掩盖了物理本质指标符号哑标和自由标 Einstein求和约定:凡在某一项内,重复一次且仅重复一次的指标,表示对该指标在它的取值范围内求和,并称这…...

索引失效情况
左或者左右模糊匹配,like %xx,like %xx% select * from student where name like %三; 原因:B是按照索引值有序排列,只能根据前缀比较来确定数据,一旦左边是模糊的,显然无法确定到底是哪个索引值 对索引字…...
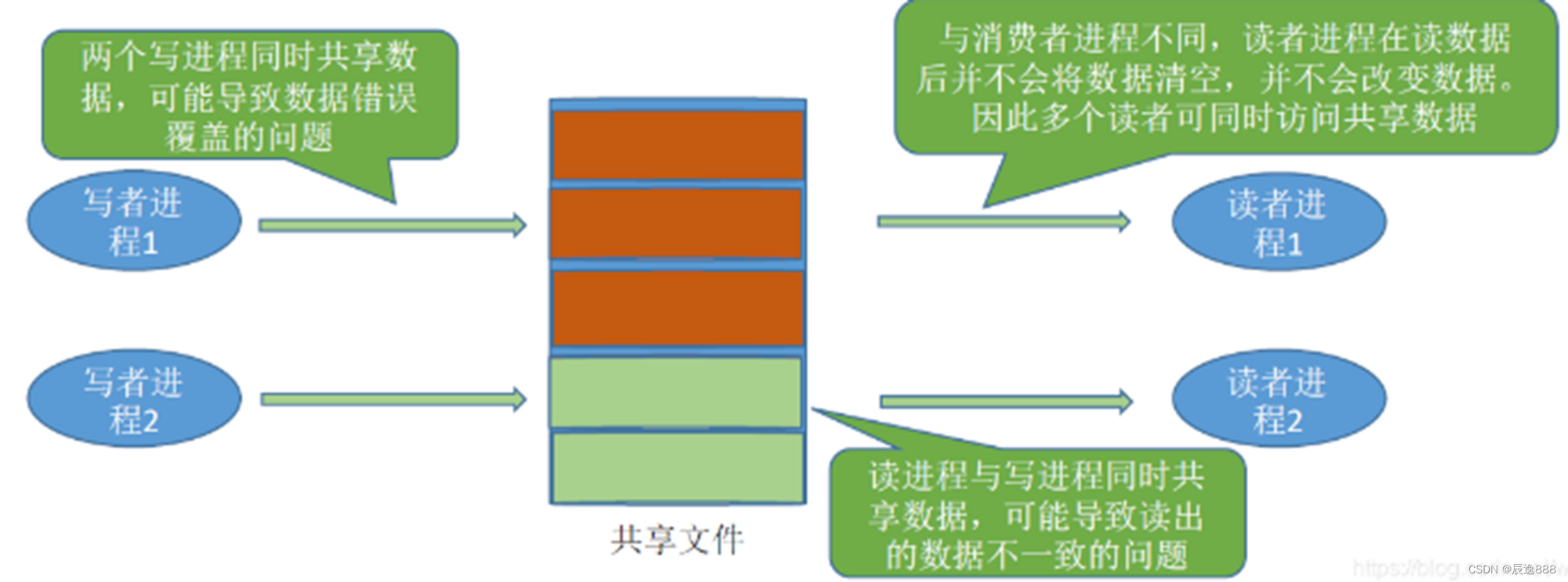
pv操作练习题
信号量解决五个哲学家吃通心面问题 题型一 有五个哲学家围坐在一圆桌旁,桌中央有盘通心面,每人面前有一只空盘于,每两人之间放一把叉子。每个哲学家思考、饥饿、然后吃通心面。为了吃面,每个哲学家必须获得两把叉子,…...

【小菜鸡刷题记】--字符串篇
【小菜鸡刷题记】:字符串 剑指 Offer 05. 替换空格剑指 Offer 58 - II.左旋转字符串剑指 Offer 20.表示数值的字符串剑指 Offer 67. 把字符串转换成整数 特此声明:题目均来自于力扣 剑指 Offer 05. 替换空格 题目链接 请实现一个函数,把字符…...
Sonar加入jenkins流水线
前提:已搭建sonarqube 1、配置sonarqube server jenkins 中manage jenkins-configure System配置sonarqube server 2、准备sonar环境 在jenkins项目的构建环境步骤中,勾选prepare SonarQube environment token需要提前在凭据里添加一个token 3、执行s…...

FSW26现金回收RS FSW43 信号和频谱分析仪
Rohde & Schwarz FSW26信号和频谱分析仪,2 Hz - 26.5 GHz 高性能 Rohde & Schwarz (R&S) FSW26 信号和频谱分析仪专为方便、准确和快速而设计。其独特的触摸屏、直观的多视图结果显示和优化的用户指南使 R&S FSW26 分析仪的操作高效方便。凭借其无…...

GraphPad Prism 9.5.1 for Mac 操作简便功能强大且实用的医学绘图分析工具
GraphPad Prism简介 GraphPad Prism是一款非常实用的统计软件,其功能非常强大,能够帮助用户进行各类科研数据的处理和分析,快速绘制出各种专业的图像和数据报告。 GraphPad Prism软件的用户界面非常友好,易于学习和操作…...

六. Activity启动模式
Task任务栈(ActivityTask) Activity属于App进程,但是Task属于操作系统,Task里面的Activity可以是属于不同的App的,所以App之间是可以相互调用的.比如:App里面可以使用打电话、地图等. 当我们查看手机后台运行的程序,他们其实就是一个个任务栈Task,我们平时可能会把他认为是一个…...
本机连接aws的ec2时报错:所选用户的用户密钥未在远程主机上注册
引言 由于工作的需要,所以需要去学习下AWS相关的知识,所以自己注册了一个AWS的账号去进行学习。 问题发现 按照启动ec2实例的步骤:选择镜像->选择系统配置->配置密钥对->配置安全组->设置存储卷大小->启动实例 在上述操作…...

谁看见我的猫照片了
今天分享一个可自由拖得动的图片效果样式。 先看效果: 谁看见我猫的照片了? 再上源码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Title</title><st…...

数据结构与算法之深度优先算法详解
深度优先算法(Depth First Search,DFS)是一种常见的图形算法,它是一种用于遍历或搜索树或图的算法。在深度优先搜索中,我们首先探索一个子树的深度,然后再回溯到父节点,接着探索另一个子树的深度…...
C# 给winfrom窗体添加皮肤控件
如何快速给C# winform添加好看的皮肤C# Winform中窗体的美化 SkinEngine的应用 皮肤控件换肤素材包,IrisSkin2.dll皮肤素材资源下载 压缩包内一共有22种皮肤素材,使用说明:把控件拖到你的form上,只需一行代码,即可实…...

数据分析真的很火吗?真的有很多企业需要这样的岗位吗?求大佬指点。
“我是去年毕业的,因为疫情影响,整个就业环境都很不好,很多企业都裁员了。加上疫情三年基本都是玩过去,也没啥一技之长,就业就更难了。听说现在做数据分析的人很多,我身边的朋友都在转行做数据分析。 其实…...
100 个 Go 错误以及如何避免:9~12
协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【OpenDocCN 饱和式翻译计划】,采用译后编辑(MTPE)流程来尽可能提升效率。 真相一旦入眼,你就再也无法视而不见。——《黑客帝国》 九、并发实践 本章涵盖 防止 …...

用户/用户组管理
用户管理 * useradd 命令添加用户,会在/etc/passwd生成用户信息,信息分为7列,被6个冒号隔开 第一列 username (login name) 第二列 密码,但是该列已经被移除,用x表示,密码信息已经存放在了/etc/shadow文…...
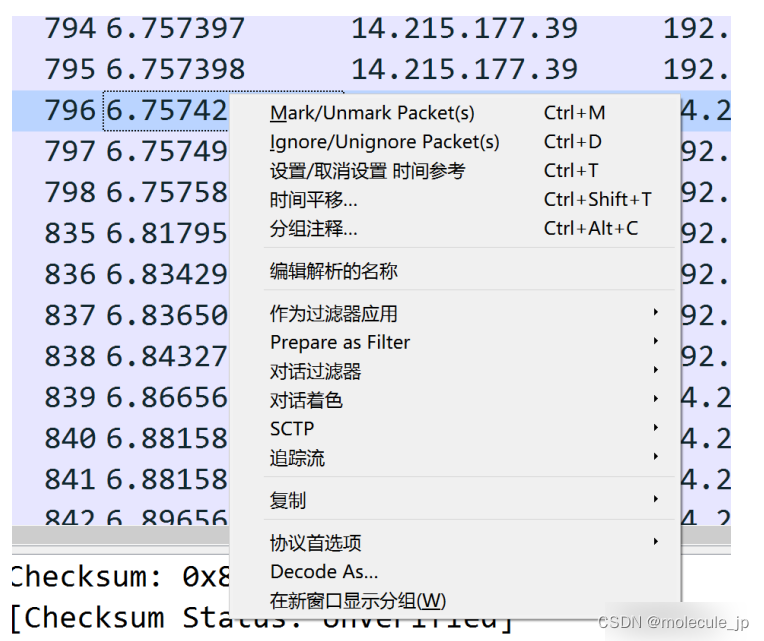
如何进行TCP抓包调试?
网络调试工具——Wireshark Wireshark 是世界上应用最广泛的网络协议分析器,它让我们在微观层面上看到整个网络正在发生的事情。 Wireshark 本身是一个开源项目,所以也得到了很多志愿者的支持。同时,Wireshark 具有丰富的功能集,…...

分享一个国内可用的ChatGPT网站,免费无限制,支持AI绘画 - AI 百晓生
背景 ChatGPT作为一种基于人工智能技术的自然语言处理工具,近期的热度直接沸腾🌋。 作为一个AI爱好者,翻遍了各大基于ChatGPT的网站,终于找到一个免费!免登陆!手机电脑通用!国内可直接对话的C…...

API安全性的要素与开发人员必修课测试
一、API安全性的要素主要包括以下几点: 1.身份验证和访问控制:API应该通过身份验证来验证请求的源,确保只有授权的用户或应用程序才能访问API。这可以通过使用API密钥、访问令牌、OAuth令牌或其他身份验证机制实现。 2.数据加密:A…...

leetcode 651. 4键键盘
651. 4键键盘 中等 102 company 微软 Microsoft company 谷歌 Google company 亚马逊 假设你有一个特殊的键盘包含下面的按键: A:在屏幕上打印一个 ‘A’。Ctrl-A:选中整个屏幕。Ctrl-C:复制选中区域到缓冲区。Ctrl-V:…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...
