第七届蓝桥杯省赛——5分小组
题目:
9名运动员参加比赛,需要分3组进行预赛。
有哪些分组的方案呢?
我们标记运动员为 A,B,C,... I
下面的程序列出了所有的分组方法。
该程序的正常输出为:
ABC DEF GHI
ABC DEG FHI
ABC DEH FGI
ABC DEI FGH
ABC DFG EHI
ABC DFH EGI
ABC DFI EGH
ABC DGH EFI
ABC DGI EFH
ABC DHI EFG
ABC EFG DHI
..... (以下省略,总共560行)。
分析:
这道题分三个组,第一个组我们让他在主函数里遍历所有可能,第二组我们建一个新的自定义函数,里面弄三个嵌套循环,求三个
步骤:

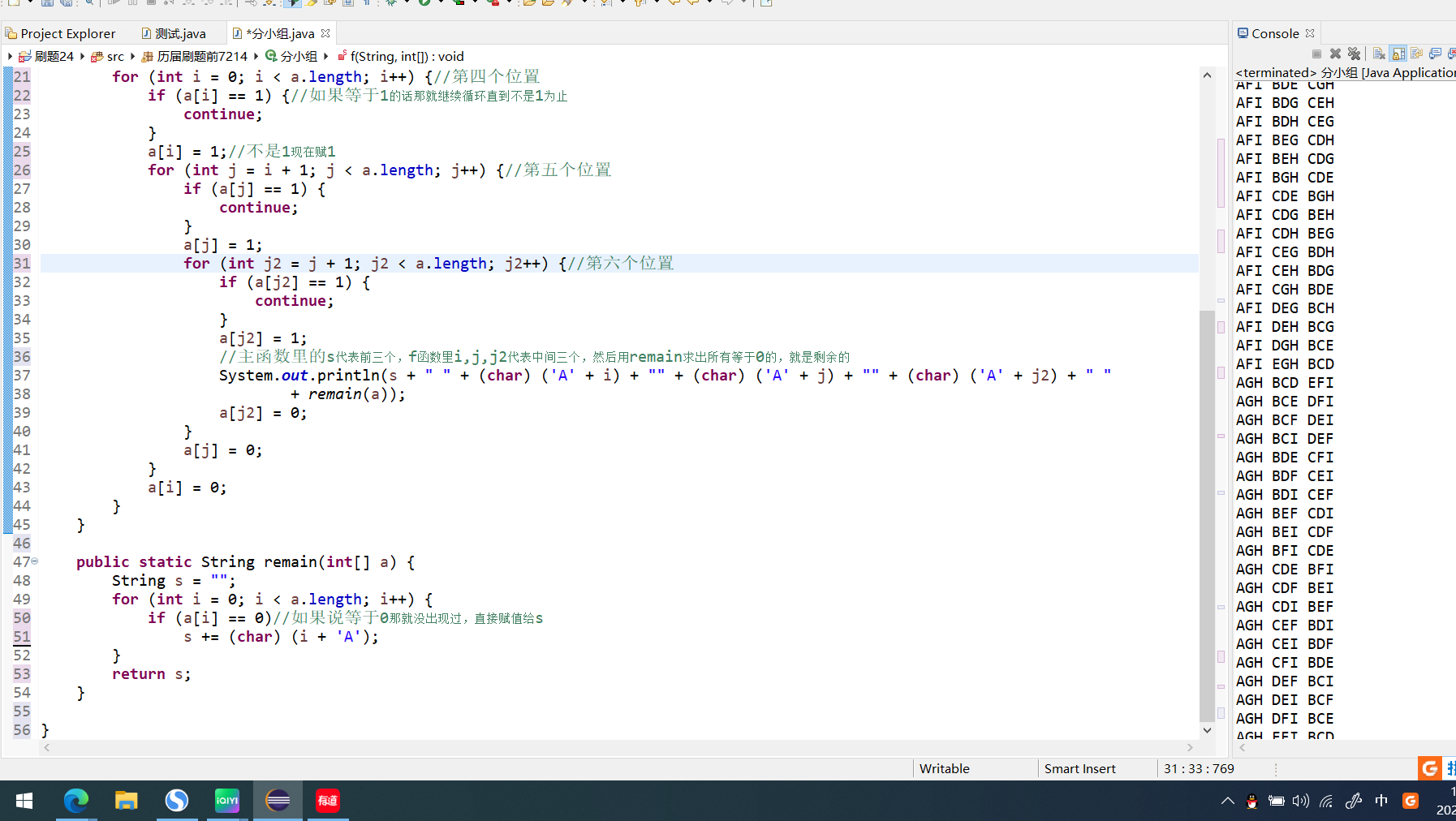
package 历届刷题前7214;public class 分小组 {public static void main(String[] args) {int[] a = new int[9];//数组用来储存9个字母a[0] = 1;//我们让第一项始终为1for (int i = 1; i < a.length; i++) {//第二个位置a[i] = 1;//每到达下一项就让这一项等于1for (int j = i + 1; j < a.length; j++) {//第三个位置a[j] = 1;//每到达下一项就让这一项等于1String s = "A" + (char) (i + 'A') + (char) (j + 'A');//第一组所有的可能f(s, a);a[j] = 0;//退出来的时候归0}a[i] = 0;//退出来的时候归0}}private static void f(String s, int[] a) {for (int i = 0; i < a.length; i++) {//第四个位置if (a[i] == 1) {//如果等于1的话那就继续循环直到不是1为止continue;}a[i] = 1;//不是1现在赋1for (int j = i + 1; j < a.length; j++) {//第五个位置if (a[j] == 1) {continue;}a[j] = 1;for (int j2 = j + 1; j2 < a.length; j2++) {//第六个位置if (a[j2] == 1) {continue;}a[j2] = 1;//主函数里的s代表前三个,f函数里i,j,j2代表中间三个,然后用remain求出所有等于0的,就是剩余的System.out.println(s + " " + (char) ('A' + i) + "" + (char) ('A' + j) + "" + (char) ('A' + j2) + " "+ remain(a));a[j2] = 0;}a[j] = 0;}a[i] = 0;}}public static String remain(int[] a) {String s = "";for (int i = 0; i < a.length; i++) {if (a[i] == 0)//如果说等于0那就没出现过,直接赋值给ss += (char) (i + 'A');}return s;}}相关文章:

第七届蓝桥杯省赛——5分小组
题目:9名运动员参加比赛,需要分3组进行预赛。有哪些分组的方案呢?我们标记运动员为 A,B,C,... I下面的程序列出了所有的分组方法。该程序的正常输出为:ABC DEF GHIABC DEG FHIABC DEH FGIABC DEI FGHABC DFG EHIABC DFH EGIABC DF…...

中国专科医院行业市场规模及未来发展趋势
中国专科医院行业市场规模及未来发展趋势中国专科医院行业在过去几年中取得了跨越式发展,市场规模不断扩大,未来的发展前景也远比过去更加乐观。根据市场调研在线网发布的2023-2029年中国专科医院行业运营现状及发展前景预测报告分析,截至2018年…...
【刷题笔记】--两数之和Ⅳ,从二叉树中找出两数之和
法一:深度搜索中序遍历双指针 思路:通过中序遍历二叉树得到一个递增的数列,再在这个递增的二叉树中找到这两数。 主要学到双指针这个方法。 对于一般数列,我们要找到两数满足其之和等于目标数,我们一般会进行暴力&a…...

浏览器渲染原理JavaScript V8引擎
浏览器渲染原理 前言 在我们面试过程中,面试官经常会问到这么一个问题,那就是从在浏览器地址栏中输入URL到页面显示,浏览器到底发生了什么? 浏览器内有哪些进程,这些进程都有些什么作用;浏览器地址输入U…...

在TheSandbox 的「BOYS PLANET」元宇宙中与你的男孩们见面吧!
世界各的男孩们成为 K-Pop 男团的旅程。 Mnet 的全球项目 BOYS PLANET 终于在 2 月 2 日首次亮相! The Sandbox 与 CJ ENM 合作,于 2 月 6 日晚上 10 点开始举办两个基于 BOYS PLANET 生存节目的虚拟体验:BOYS PLANET:BOYS LAND 和…...

数据结构与算法:java对象的比较
1.基本类型的比较 在Java中,基本类型的对象可以直接比较大小。 public class TestCompare {public static void main(String[] args) {int a 10;int b 20;System.out.println(a > b);System.out.println(a < b);System.out.println(a b);char c1 A;char…...

python(16)--类
一、类的基本操作1.定义一个类格式:class Classname( ):内容💎鄙人目前还是一名学生,最熟悉的也就是学校了,所以就以学校为例子来建立一个类吧class School():headline"帝国理工大学"def schoolmotto(self):…...
Calico 介绍与原理(二))
CNI 网络流量分析(七)Calico 介绍与原理(二)
文章目录CNI 网络流量分析(七)Calico 介绍与原理(二)CNIIPAM指定 IP指定非 IPAM IPCNI 网络流量分析(七)Calico 介绍与原理(二) CNI 支持多种 datapath,默认是 linuxDa…...

API安全的最大威胁:三体攻击
最近《三体》火的一塌糊涂,动画片、电视剧和书都受到了大家的喜爱。在API安全上,最近也发现了三体攻击。 当然了,肯定是不来自于三体人的攻击,这里的三体攻击指的是(trinity,也称三位一体攻击),是一个新的攻击手法。具体的情况老李也找到了相关的介绍,下面就分享给大…...

分布式事务解决方案——TCC
TCC是Try、Confirm、Cancel三个词语的缩写,TCC要求每个分支事务实现三个操作:预处理Try、确认Confirm、撤销Cancel。1、Try 阶段是做业务检查(一致性)及资源预留(隔离),此阶段仅是一个初步操作,它和后续的Confirm一起才能真正构成…...

ITSS认证分为几个级别,哪个级别最高
一、什么是ITSS ITSS( 信息技术服务标准,简称ITSS)是国内第一套成体系和综合配套的信息技术服务标准库,全面规范了IT服务产品及其组成要素,用于指导实施标准化和可信赖的IT服务。 ITSS是在工业和信息化部、国家标准化管理委员会的联合指导下…...

ZigBee案例笔记 - USART
文章目录1.串行通信接口简述2.串行通信接口寄存器U0CSR (0x86) -USART 0 控制和状态U0UCR (0xC4)–USART 0 UART 控制U0GCR (0xC5)–USART 0 通用控制U0BUF (0xC1) – USART 0 接收/传送数据缓存U0BAUD (0xC2) – USART 0 波特率控制3.设置串行通信接口比特率控制寄存器4.外设I…...

java | 基于Redis的分布式锁实现①
前言 首先,为了确保分布式锁可用,我们至少要确保锁的实现同时满足以下四个条件: 互斥性。在任意时刻,只有一个客户端能持有锁。不会发生死锁。即使有一个客户端在持有锁的期间崩溃而没有主动解锁,也能保证后续其他客户…...

十六、基于FPGA的CRC校验设计实现
1,CRC校验循环冗余校验(Cyclic Redundancy Check, CRC)是一种根据网络数据包或计算机文件等数据产生简短固定位数校验码的一种信道编码技术,主要用来检测或校验数据传输或者保存后可能出现的错误。它是利用除法及余数的…...

2022爱分析 · DataOps厂商全景报告 | 爱分析报告
报告编委 李喆 爱分析合伙人&首席分析师 廖耘加 爱分析分析师 目录 1. 研究范围定义 2. 市场洞察 3. 厂商全景地图 4. 市场分析与厂商评估 5. 入选厂商列表 1. 研究范围定义 研究范围 在后疫情时代,以数据分析为代表的数据消费场景日益丰富&…...

京东前端react面试题及答案
useEffect 与 useLayoutEffect 的区别 (1)共同点 运用效果: useEffect 与 useLayoutEffect 两者都是用于处理副作用,这些副作用包括改变 DOM、设置订阅、操作定时器等。在函数组件内部操作副作用是不被允许的,所以需…...
TongWeb8数据源相关问题
问题一:数据源连接不足当TongWeb数据源连接用完时,除了监控中看到连接占用高以外,日志中会有如下提示信息。2023-02-14 10:24:43 [WARN] - com.tongweb.web.jdbc.pool.PoolExhaustedException: [TW-0.0.0.0-8088-3] Timeout: Pool empty. Una…...
关于最近大热的AI,你怎么看?
AI人工智能,相信大家都不陌生,也都接触过不少。但是最近小编在网上冲浪的时候发现各大媒体又掀起了一阵AI热潮,AI不是很常见了吗?是又有什么新的发展吗? 带着强烈的好奇心,我在地铁上读完了一篇关于Chatgp…...

25.架构和软件产品线
文章目录25 Architecture and Software Product Lines架构和软件产品线25.1 An Example of Product Line Variability 产品线可变性的一个例子25.2 What Makes a Software Product Line Work? 软件产品线的工作原理是什么?25.3 Product Line Scope 产品线范围25.4 …...
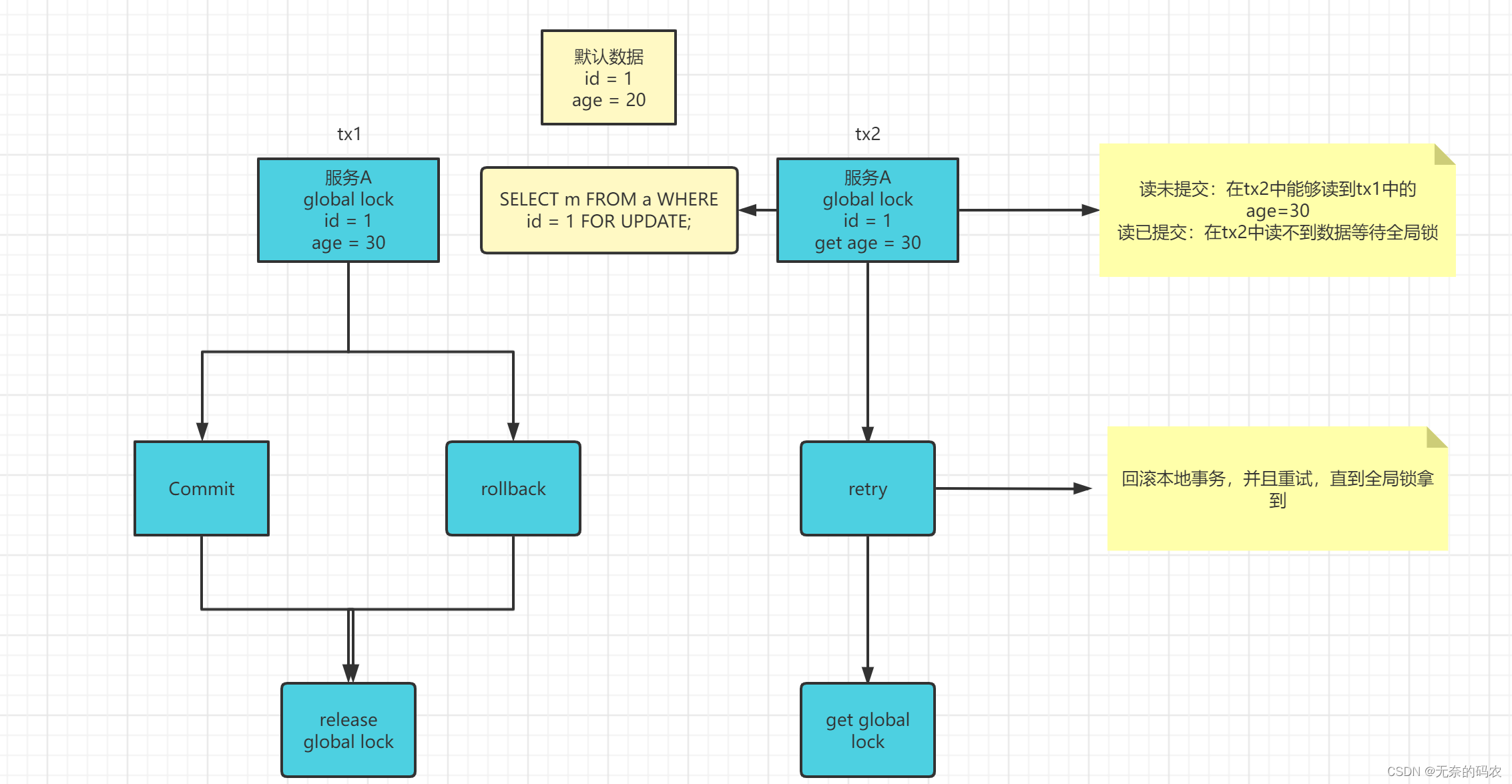
Seata-server 源码学习(一)
Seata源码学习引入 学习了Seata的应用以后,我们从这开始要开始分析Seata的源码相关内容 源码下载 官方地址:https://seata.io/zh-cn/blog/download.html 通过idea打开seata-1.4.2版本的源码 回顾AT模式 其实在之前的应用课程中,我们已经用…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...
