数据结构之初识树与堆
前言:前面学习了顺序表,队列,栈,链表,我们知道他们都是一种线性表,是一种线性结构,而除此之外,仍有许多我们还没认识的结构,比如树形结构,不同于线性结构,树形结构就如同他的名字,结构相对更加复杂,是一种倒着的树的数据结构。
目录
1,什么是树?
2.树的相关概念
3.树的定义
4.二叉树
特殊的二叉树:
2.二叉树的存储方式
5.堆
结构体定义与函数接口
堆的初始化
堆的销毁
入堆
向上调整算法
向下调整算法
出堆
1,什么是树?
树是一种非线性的数据结构,它是由n(n>0)个有限节点组成一个具有层次关系的集合,把它叫做书是因为它看起来像一颗倒挂着的树(个人感觉也像树根部的形状),也就是他是根朝上,叶子朝下。
树结构拥有自己的一些独特性质:
.有一个特殊的节点,称为根节点,根节点没有前驱节点
.除根结点外,其余节点被分为M(M>0)个互不相交的集合T1,T2,......Tm,其中每个集合我们可以认为也是一个类似主树的子树,每个子树的节点有且只有一个前驱,可以有0或多个后继节点。
.树是递归定义的,因为它的套娃结构,大树里住着小树。
如下图一根秃了的倒着的树与树结构的对比
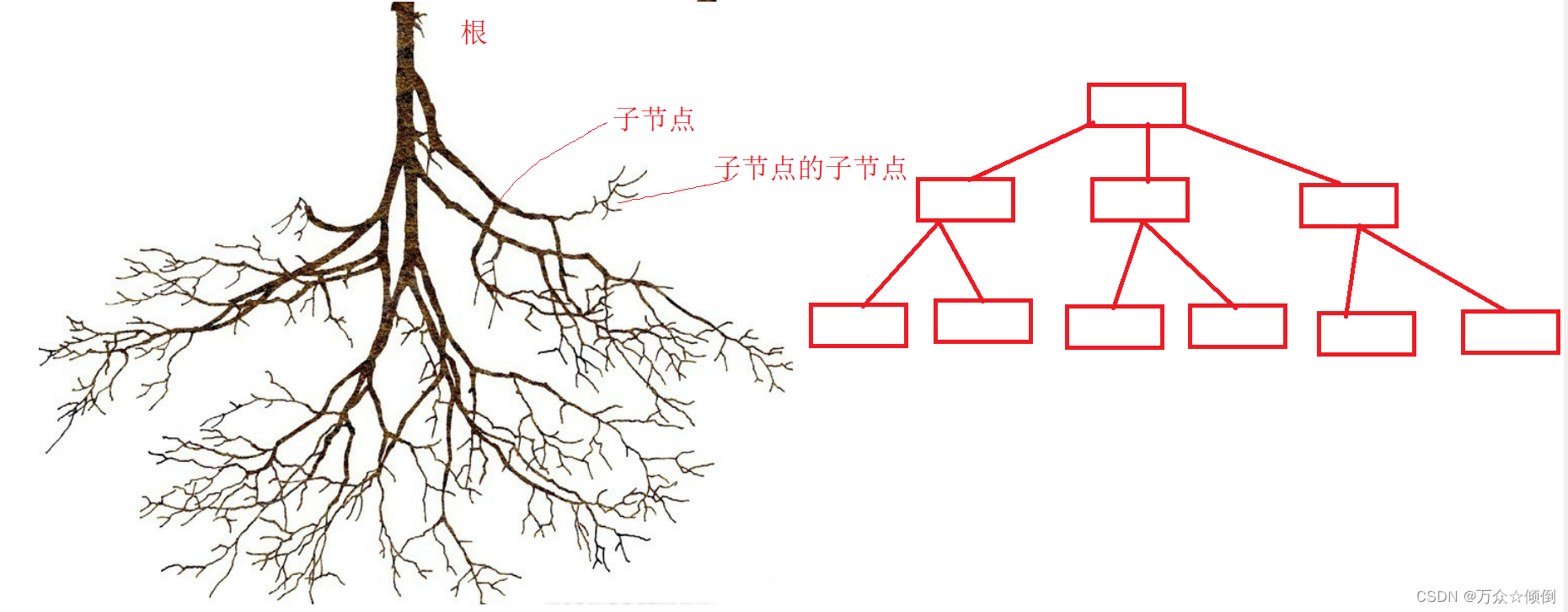
注意:树型结构里面是不能出现子树相交的
不仅仅对于树形结构是这样,树也不能出现一个枝干长到另一个枝干上(可能存在变异)。
2.树的相关概念
树的某些相关概念是以人类的血缘关系为样例所命名:

我们知道树是一种非线性的数据结构,它是由n(n>=0)个结点的有限集合。
当n=0时称为空树。在任何一棵非空树中:1. 有且只有一个特定的称为 根(root) 的结点;2. 当n>1时,其余结点可分为m(m>0)个 互不相交 的有限集,其中每一个集合又是一棵树,并且成为 根的子树(subtree) 。
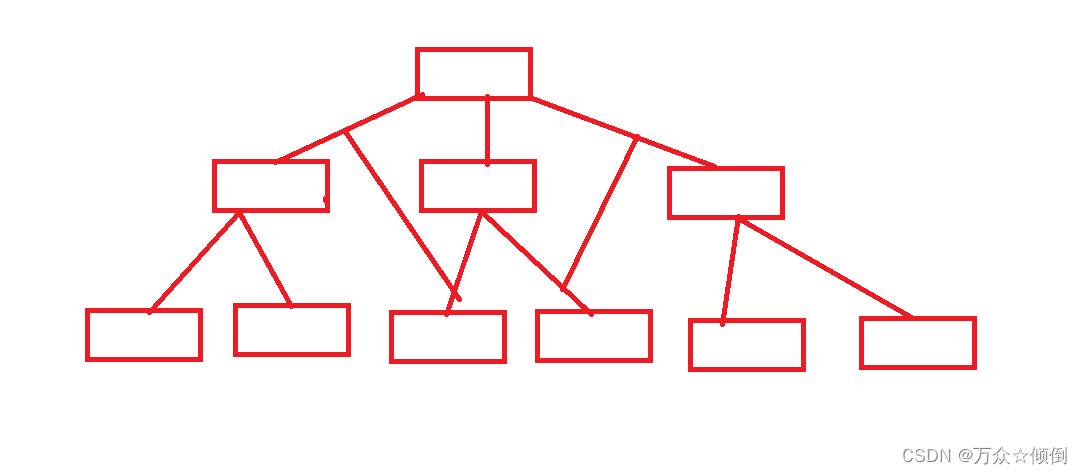
结点的度:结点拥有的子树数称为结点的 度(Degree)如上图D的度为3,A度为2.
树的度: 是树内各结点的度的最大值。如D为3
度为0的结点成为 叶节点(Leaf) 或者 终端结点 ,除根结点外,分支结点也称为 内部结点 。如上图的G H I。
结点子树的根称为该结点的 孩子(Child)。如A的孩子B,C
相应的该结点称为孩子的 双亲(Parent) 。如D的双亲为B
同一个双亲之间的孩子之间互称为 兄弟(Sibling)。B与C互为兄弟
结点的 祖先 是指从根到该结点所经历的所有结点.
反之,以该结点为根的子树中的任意一结点称为该节点的 子孙 。
树的层次:从根开始,根为第一层,根的节点为第二层,以此类推。
树的深度:树中结点的最大层次称为树的 深度(Depth) 或者高度,根据树中结点是否可以交换分为有序树和无序树。
堂兄弟节点:双亲在同一层的节点互为堂兄弟。如D,E。
森林 :是指的多棵互不相交的树。
路径和路径长度: 树中两个结点之间的 路径 是由这两个结点之间所经过的结点序列构成的,而 路径长度 是路径上所经过的 边的个数 。
3.树的定义
因为树有很多节点,按照之前的链表他们定义结点的方法,没接触前树我们可能这样定义:
struct TreeNode
{int data;struct TreeNode*child1;struct TreeNode*child2;
//......
}但其实不太可能。人们总结了许多定义树的结构的方法:
1.如果明确了树的度,那么可以定义。(根据树的度来定义节点个数,但是不太能表现树)
2.用顺序表来存放孩子。
struct TreeNode
{int data;Seqlist childArr;
}3.双亲表示法。(每个位置只存储该节点的父节点):用数组存放双亲的下标。
并查集这里就是只存储父亲的下标。

4.左孩子右兄弟方法:比较牛的一种方法,也是一种较优的方法:每一个节点只存放他的第一个孩子节点和下一个兄弟节点。
struct TreeNode{struct TreeNode*firstchid;//第一个孩子节点struct TreeNode*nextbrother;//指向下一个兄弟节点int data;//节点的数据域}
对于森林,一般是文件系统结构。
4.二叉树
概念:一种特殊的树的结构,一个二叉树是节点的一个有限集合:
1.要么为空
2.有一个根节点加上两个子树(左右子树)组成。如图:

我们可以看到:
1.二叉树不存在度大于2的节点
2.二叉树有左右之分,左边的节点叫左孩子,右边的节点叫右孩子,次序不能颠倒,因此是一个有序树。
特殊的二叉树:
1.满二叉树
概念:一个二叉树,如果每层结点数都达到最大值,那么这个树就是满二叉树。也就是说,如果一个二叉树的层数为K,那么总结点数为,(2^k)-1),等比求和公式可推导出,第N层的节点数为2^(n-1).

2.完全二叉树
概念:相对于满二叉树的最后一行,最后一行不全满,且结点依次从左到右,就是一个完全二叉树。
若一个完全二叉树的层数为k,那么他的k-1层以上的每一层都是满的。
满二叉树是一种特殊的完全二叉树。

若深度为h,节点范围【2^(h-1),2^h-1】.
2.二叉树的存储方式
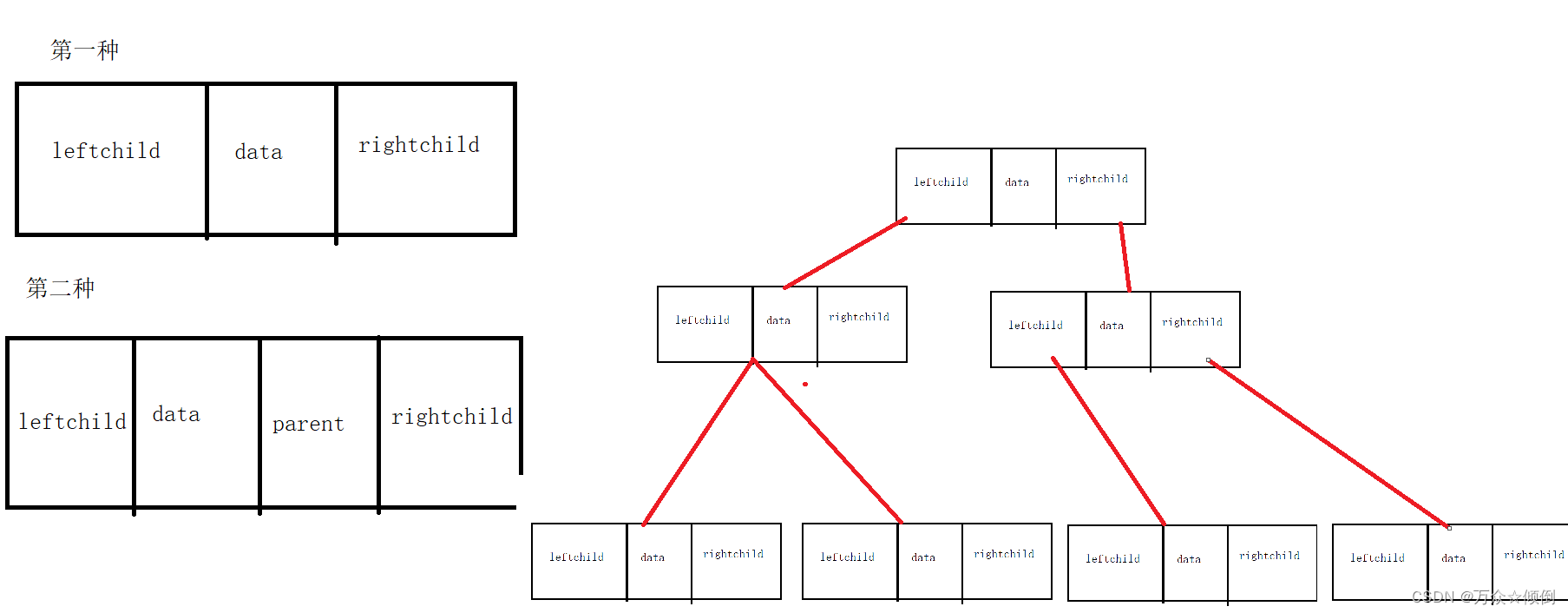
1.可用二叉链表来表示(有的地方是三叉链表,多了一个结点指向前面的双亲)。
2.可用数组来表示。
用数组存放右几个优点:
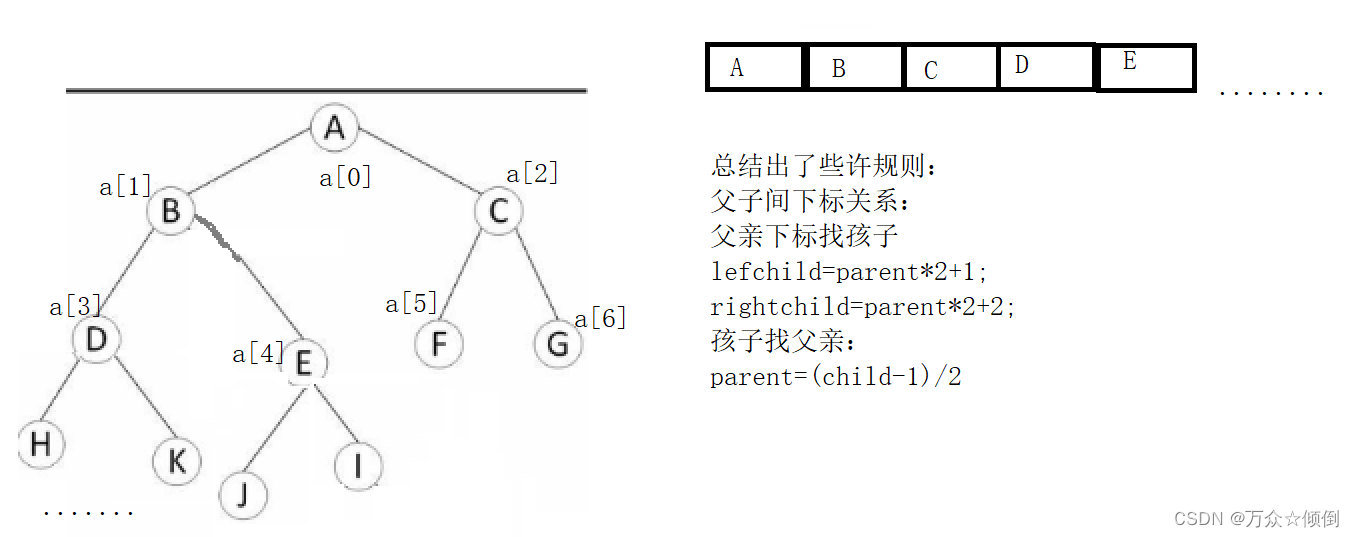
对于这种存储,比较适合完全二叉树来存储。,因为若有一个双亲没有孩子节点,对于数组这种下表表示双亲存在问题。
5.堆
知道以上的存储方法,对于完全二叉树,有一个叫做堆的结构,堆本质就是一个完全二叉树,
堆分两种:1.大堆 2.小堆
除了是完全二叉树,大堆需满足任何一个双亲都大于等于孩子,对于小堆,任何一个双亲都小于等于孩子。
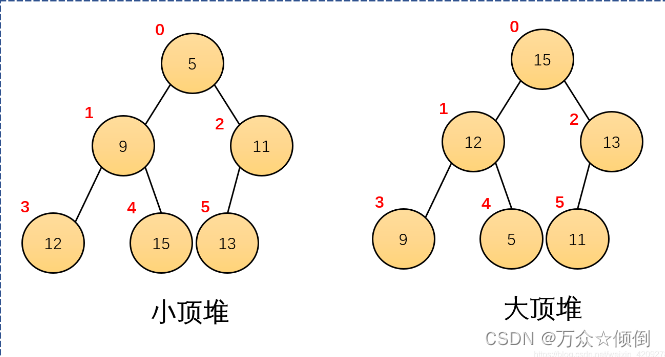
我们实现堆就用数组来实现的:这里以实现小堆为例
结构体定义与函数接口
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef int HPDATAtype;
typedef struct Heap
{HPDATAtype *a;int size;int capacity;
}HP;void Heapinit(HP* f);
void Heapdestroy(HP* f);
void Heappop(HP* f);
void Heappush(HP* f , HPDATAtype x);
堆的初始化
void Heapinit(HP* f)
{//初始有4个空间assert(f);f->a = NULL;f->size = 0;f->capacity = 0;
}堆的销毁
void Heapdestroy(HP* f)
{assert(f->a);free(f->a);f->a = NULL;
}入堆
void Heappush(HP* f, HPDATAtype x)
{assert(f);if (f->capacity == f->size){int newcapacity = f->capacity = 0 ? 4 : f->capacity*2;HPDATAtype* newnode = (HPDATAtype*)malloc(newcapacity);if (newnode == NULL){perror("扩容失败\n");return;}f->a = newnode;f->capacity = f->capacity*2;}f->a[f->size] = x;f->size++;//向上调整算法Adjustup(f->a, f->size - 1);//向下调整算法//Adjustdown(f->a, f->size - 1);
}在这里在入堆之后,也就是元素赋值到数组之后,根据你对数组的调整,也就是所说的向上调整算法,和向下调整算法,决定是小堆,还是大堆。
向上调整算法
我们这里通过对树所对应的数组元素的关系寻找父亲。
void Adjustup(HPDATAtype*a, int child)
{//根据孩子zhaofuqinint parent = (child - 1) / 2;while (child>0){if ( a[child]<a[parent]){HPDATAtype p = a[child];a [child] = a[parent];a[parent]=p;child = parent;parent = (child - 1) / 2;}else {break;}}
}向下调整算法
void Adjustdown(HPDATAtype* a, int child)
{//根据孩子找父亲int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent]){int tmp = a[child];a[child] = a[parent];a[parent] = tmp; child = parent;parent = (child - 1) / 2;}else{break;}}}出堆
出堆就是最后一个元素换到第一个元素,在size--,之后在进行调整。
void Heappop(HP* f){assert(f);//堆顶元素出堆,最小元素出堆assert(f->size);int tmp = f->a[0];f->a[0] = f->a[f->size - 1];f->a[f->size - 1] = tmp;f->size--;//向上调整for (int i = 0; i < f->size; i++){Adjustup(f->a, i);}
};堆的应用:
优先级队列的实现 堆排序算法 获取特定范围的值
相关文章:

数据结构之初识树与堆
前言:前面学习了顺序表,队列,栈,链表,我们知道他们都是一种线性表,是一种线性结构,而除此之外,仍有许多我们还没认识的结构,比如树形结构,不同于线性结构&…...

虚拟化技术 — VirtIO 虚拟设备接口标准
目录 文章目录 目录VirtIOVirtIO 虚拟设备接口标准VirtIO 的前后端分层架构标准VirtIO 的数控路径分离架构标准VirtIO 的传输层标准VirtIO 标准在 Linux 中的实现VirtIO VirtIO 由 Rusty Russell 开发,最初是为了支持自己开发的 lguest Hypervisor,其设计目标是在虚拟化环境…...
Dubbo——SpringBoot集成Dubbo(@Autowired和@Reference的区别、Dubbo的服务治理)
Dubbo——原生API实现远程调用_Strine的博客-CSDN博客 在上一篇文章中我们讲了如何使用原生API发起远程调用,显然这种方式肯定是非常麻烦的,因此我们这里就讲如何使用SpringBoot去集成Dubbo将这些配置简化。 生产者服务 添加配置文件 dubbo:applicat…...
高并发系统的三把利器
目录 1.限流 2.缓存 2.1.缓存的使用场景 3.降级 3.1.什么是降级? 3.2.服务降级方式 4.其他高并发手段 4.1. 集群 4.2.拆分 4.2.1 应用拆分 4.2.2 数据库 4.3. 静态化 4.4.削峰 4.5.限流 5.总结 参考 保护高并发系统的三大利器:限流、熔…...

AppiumWinAppDriver自动化测试 Failed to locate opened application window with appid问题
问题产生原因:1.期望能力选项参数丢失 例如:capabilities.setCapability("appWorkingDir", "C:\\Program Files (x86)\\Tencent\\app")) 某些app需要设置目录属性才可以启动。 问题产生原因:2.访问权限不足 例如&…...
渗透测试--6.1.aircrack-ng破解wifi密码
目录 1.Aircrack-ng简介 1.1 airdump-ng 1.2 aireplay-ng 1.3 aircrack-ng 2.Deauth攻击 3.aircrack-ng工具破解无线网络密码 步骤一:虚拟机连接实验需要用到的网卡 步骤二:设置网卡为监听模式 步骤三:使用wlan0mon网卡扫描附近wif…...
C++中的继承、以及赋值兼容转换。
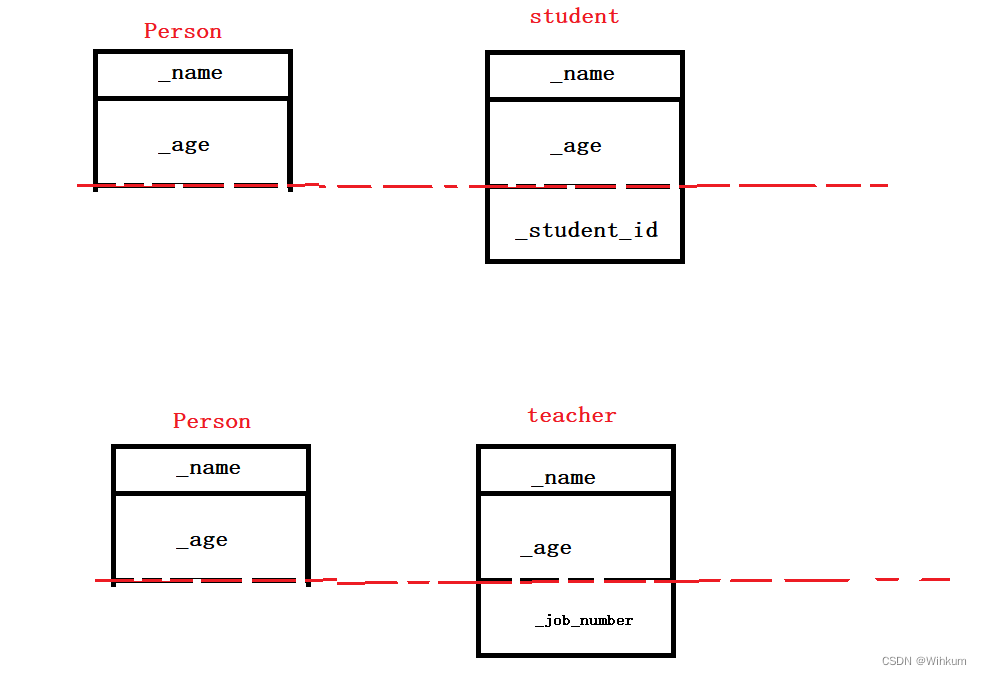
一、继承的概念及定义 继承可以使代码复用,允许在保持原有类特性的基础上进行扩展。 举个例子:就好比我现在要封装老师、学生等这些人的属性和方法,但是这些人都有重复的属性和方法,比如name、age、sex等等,那么我可…...

js浏览器实现简单的实时扫一扫功能
描述:利用vue-qrcode-reader插件实现h5/wap端简单的扫一扫功能 参考文档:https://gruhn.github.io/vue-qrcode-reader/demos/Validate.html官方文档 安装插件 npm i --save vue3-qr-reader 或 yarn add vue3-qr-reader 注意项目运行必须在https下&…...
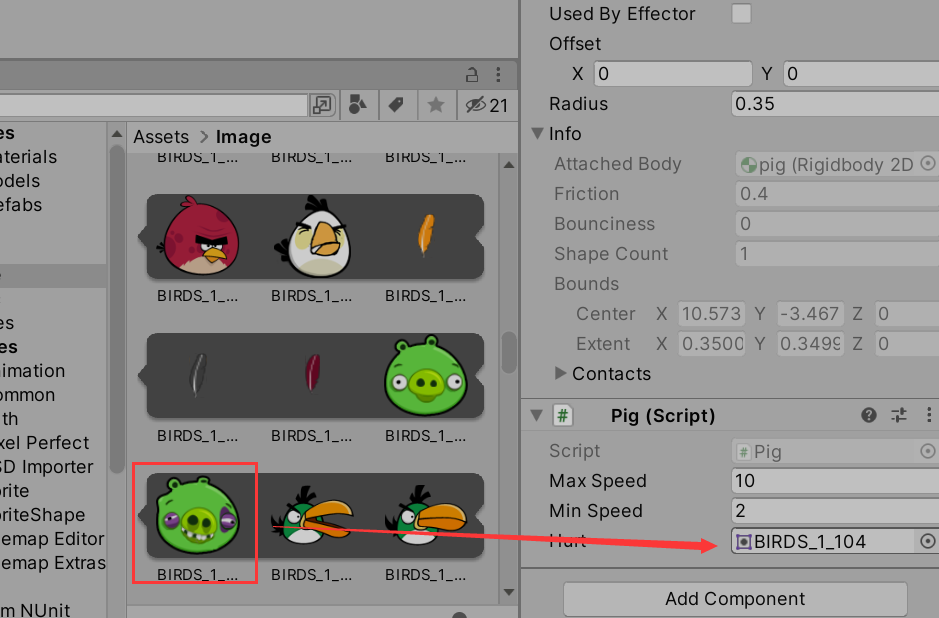
unity愤怒的小鸟学习制作(二)
终于又开始了啦啦啦,我有一个自己的相机了,真开心,诶嘿 视频链接和素材如下:视频 小鸟的飞出 想要让小鸟在拉开弹弓之后能飞出去,就必须让这个组件失活,如下 所以我们更改脚本内容,加入&#…...

干外包3年,彻底寄了...
先说一下自己的情况,大专生,18年通过校招进入湖南某软件公司,干了接近6年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了6年的功能测试&…...
)
软考高项论文范文(三)
论信息系统项目的沟通管理 【摘要】(该摘要共313个字符) 本文讨论了ⅹⅹ省社保系统民政统一软件开发项目的沟通管理。该项目是在国家大社会保险政策指导下于2018年10月份正式启动的。该系统为用户提供了优抚安置、救灾救济等十大主要业务功能。在本文中…...

浅谈谈谈OTA召回2023
近日,国家市场监督管理总局发布特斯拉召回公告,一下子掀起了互联网热议,这次召回的范围是在2019年1月12日至2023年4月24日期间国内销售特斯拉汽车(含国产和进口共计110万辆车),在这个召回公告中有两点值得关…...
【GDI+】旋转文本/斜体字
一、需求 想要绘制如下所示的斜体字,45度 二、分析&思路 Graphics类有个 RotateTransform方法,可以传入任意角度的值来旋转画板。但是这个方法的旋转中心是画板的左上角,所以直接单单用这个方法不能满足我们的需求。此外, G…...

python3 面试题总结
Python global 语句的作用lambda 匿名函数好处Python 错误处理Python 内置错误类型简述 any() 和 all() 方法Python 中什么元素为假?提高 Python 运行效率的方法Python 单例模式为什么 Python 不提供函数重载实例方法/静态方法/类方法__new__和 __init __方法的区别…...

select poll epoll有什么区别
select/poll select 实现多路复用的方式是,将已连接的 Socket 都放到一个文件描述符集合,然后调用 select 函数将文件描述符集合拷贝到内核里,让内核来检查是否有网络事件产生,检查的方式很粗暴,就是通过遍历文件描述…...

Java基础面试题突击系列1
👩🏻 作者:一只IT攻城狮 ,关注我不迷路 ❤️《java面试核心知识》突击系列,持续更新… 💐 面试必知必会学习路线:Java技术栈面试系列SpringCloud项目实战学习路线 📝再小的收获x365天…...

go-zero和dtm分布式事务实现
go-zero是一个基于Go语言的微服务开发框架,而DTM(Distributed Transaction Manager)是一个分布式事务管理器,用于实现跨多个微服务的分布式事务。 下面是使用go-zero和DTM实现分布式事务的基本步骤: 安装和配置DTM&am…...

Springboot +Flowable,会签、或签简单使用(一)
一.简介 **会签:**在一个流程中的某一个 Task 上,这个 Task 需要多个用户审批,当多个用户全部审批通过,或者多个用户中的某几个用户审批通过,就算通过。 例如:之前的请假流程,假设这个请假流程…...

银行面试中的即兴演讲技巧,你了解吗
面试的主要形式有无领导小组讨论、结构化和半结构化面试,一些银行还会出现辩论赛、角色扮演、即兴演讲等形式,今天小编就来聊一聊面试中的即兴演讲,从如信银行考试中心了解到: 简单来说即兴演讲就是在特定情境下,自发或…...

基于LT6911UXC的LVDS视频接口调试经验
文章目录 概要整体架构流程技术名词解释技术细节小结概要 项目方案采用龙讯半导体LT6911系列 整体架构流程 CPU主芯片采用飞腾,显卡采用GP102,由于项目需要LVDS接口,GP102的HDMI口输出后经过LT6911UXC转成LVDS输出 在本方案中有两种显示屏;一个是10.4寸,一个是15.6寸。…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...
