《统计学习方法》——隐马尔可夫模型(上)
引言
这是《统计学习方法》第二版的读书笔记,由于包含书上所有公式的推导和大量的图示,因此文章较长,正文分成三篇,以及课后习题解答,在习题解答中用Numpy实现了维特比算法和前向后向算法。
- 《统计学习方法》——隐马尔可夫模型(上)
- 《统计学习方法》——隐马尔可夫模型(中)
- 《统计学习方法》——隐马尔可夫模型(下)
- 《统计学习方法》——隐马尔可夫模型#习题解答#
隐马尔可夫模型(Hidden Markov Model,HMM)是描述隐藏的马尔可夫链随机生成观测数据过程的模型。
前置知识
马尔可夫链
马尔可夫链(Markov chain)又称离散时间马尔可夫链,使用 t t t来表示时刻,用 X t X_t Xt来表示在时刻 t t t链的状态,假定所有可能状态组成的有限集合 S \cal S S称为状态空间。
马尔可夫链为状态空间中从一个状态到另一个状态的转换的随机过程。
在马尔可夫链的每一步,根据概率分布,可以从一个状态变到另一个状态,也可以保存当前状态。状态的概率叫做转移,状态改变的概率相关的概率就转移概率。
描述当前状态为 i i i,下一个状态为 j j j的转移概率 p i j p_{ij} pij定义为:
p i j = P ( X t + 1 = j ∣ X t = i ) , i , j ∈ S p_{ij} =P(X_{t+1}=j|X_t=i), \qquad i,j \in \cal S pij=P(Xt+1=j∣Xt=i),i,j∈S
马尔可夫链的核心假设是,只要时刻 t t t的状态为 i i i,不论过去发生了什么,也不论链是如何到达状态 i i i的,下一个时刻转移到状态 j j j的概率就一定是状态转移概率 p i j p_{ij} pij。即,该过程要求具备“无记忆”的性质:下一状态的概率分布只能由当前状态决定,与时间序列上它前面的事件无关。这种无记忆性称为马尔可夫性质。在数学上表示为:
P ( X t + 1 = j ∣ X t = i , X t − 1 = i n − 1 , ⋯ , X 0 = i 0 ) = P ( X t + 1 = j ∣ X t = i ) = p i j P(X_{t+1}=j|X_t=i,X_{t-1}=i_{n-1},\cdots,X_0=i_0) = P(X_{t+1}=j|X_t=i)=p_{ij} P(Xt+1=j∣Xt=i,Xt−1=in−1,⋯,X0=i0)=P(Xt+1=j∣Xt=i)=pij
转移概率 P i j P_{ij} Pij一定是非负的,且和为1:
∑ j p i j = 1 \sum_j p_{ij} = 1 j∑pij=1
下一个状态可能和当前状态一样,即状态没有发生变化,我们也认为状态发生了一次特殊的转移(自身转移)。
总结一下,一个马尔可夫链模型由以下特征确定:
- 状态集合 S \cal S S;
- 可能发生状态转移 ( i , j ) (i,j) (i,j)的集合,即由所有 p i j > 0 p_{ij} > 0 pij>0的 ( i , j ) (i,j) (i,j)组成;
- p i j p_{ij} pij的取值为正;
马尔可夫链可以由转移概率矩阵所刻画,它是一个简单的二元矩阵,其第 i i i行第 j j j列的元素为 p i j p_{ij} pij,假设共有 m m m个状态:
[ p 11 p 12 ⋯ p 1 m p 21 p 22 ⋯ p 2 m ⋮ ⋮ ⋮ ⋮ p m 1 p m 2 ⋯ p m m ] \begin{bmatrix} p_{11} & p_{12} & \cdots & p_{1m} \\ p_{21} & p_{22} & \cdots & p_{2m} \\ \vdots & \vdots & \vdots & \vdots \\ p_{m1} & p_{m2} & \cdots & p_{mm} \\ \end{bmatrix} p11p21⋮pm1p12p22⋮pm2⋯⋯⋮⋯p1mp2m⋮pmm
也可以用转移概率图表示马尔可夫链,图中用节点表示状态,连接节点的(有向)弧线表示可能发生的转移,将 p i j p_{ij} pij的数值标记在相应的弧线旁边。
比如下面来自维基百科的一个例子,它表示一个具有两个状态转换的马尔可夫链:

概率图模型
概率图模型(probabilistic graphical models)是概率分布的图形表示,它非常方便我们分析模型的性质,尤其是条件独立性质。
和我们数据结构中学的图一样,一个图由节点、节点间的边组成。概率图模型中,每个节点表示一个随机变量,边表示这些变量之间的概率关系,缺失的边表示条件独立假设。
概率图主要分为两大类:有向图模型,也称为贝叶斯网络(实际上和贝叶斯关系不大);无向图模型,也称为马尔可夫随机场(名字也没那么直观)。
这里主要简单介绍下有向图模型,因为HMM可以通过它进行表示。它的一些概念有助于后面的公式推理。
首先介绍下 条件独立(conditional independence, CI) 的概念。
我们先来回顾下独立的概念,假设有两个随机变量 a , b a,b a,b相互独立的话,有
p ( a , b ) = p ( a ) p ( b ) p(a,b)= p(a)p(b) p(a,b)=p(a)p(b)
如果此时求给定 b b b的条件下 a a a的概率:
p ( a ∣ b ) = p ( a , b ) p ( b ) = p ( a ) p ( b ) p ( b ) = p ( a ) (p1) p(a|b) = \frac{p(a,b)}{p(b)} = \frac{p(a)p(b)}{p(b)} = p(a) \tag{p1} p(a∣b)=p(b)p(a,b)=p(b)p(a)p(b)=p(a)(p1)
即不管 b b b的取值如何,都不影响 a a a发生的概率。也可以说 a a a条件独立于 b b b。
现在假设有三个变量 a , b , c a,b,c a,b,c,假设给定 b , c b,c b,c的条件下 a a a的条件分布不依赖于 b b b的值,即
p ( a ∣ b , c ) = p ( a ∣ c ) (p2) p(a|b,c) = p(a|c) \tag{p2} p(a∣b,c)=p(a∣c)(p2)
也就是说,在给定 c c c的条件下, a a a条件独立于 b b b。在给定 c c c的条件下, b b b作为条件的取值不会影响 p ( a ∣ c ) p(a|c) p(a∣c)。
我们考虑将 p ( a , b ∣ c ) p(a,b|c) p(a,b∣c)展开:
p ( a , b ∣ c ) = p ( a ∣ b , c ) p ( b ∣ c ) = p ( a ∣ c ) p ( b ∣ c ) (p3) p(a,b|c) = p(a|b,c)p(b|c) = p(a|c)p(b|c) \tag{p3} p(a,b∣c)=p(a∣b,c)p(b∣c)=p(a∣c)p(b∣c)(p3)
( p 2 ) (p2) (p2)和 ( p 3 ) (p3) (p3)都是在这种情况下条件独立的不同描述。
注意条件独立中的条件二字,比如这里都是在以 c c c为条件的前提下,而且是对于 c c c的所有取值都成立。
记为
a ⊥ b ∣ c a \,\bot \,b \,|\, c a⊥b∣c
表示给定 c c c的条件下 a a a和 v v v条件独立。
我们以此为基础再来看下马尔可夫链,假设 x t + 1 ⊥ x 1 : t − 1 ∣ x t x_{t+1} \,\bot \,x_{1:t-1} \, | \, x_t xt+1⊥x1:t−1∣xt,即下一时刻仅依赖于当前时刻,和所有的之前时刻无关,这就是(一阶)马尔可夫假设。
基于该假设,结合链式法则, x 1 : N x_{1:N} x1:N的联合概率分布可以写成:
p ( x 1 : N ) = p ( x 1 ) ∏ t = 2 N p ( x t ∣ x 1 : t − 1 ) = p ( x 1 ) ∏ t = 2 N p ( x t ∣ x t − 1 ) (p4) p(x_{1:N})=p(x_1)\prod_{t=2}^N p(x_t|x_{1:t-1}) = p(x_1)\prod _{t=2}^N p(x_t|x_{t-1}) \tag{p4} p(x1:N)=p(x1)t=2∏Np(xt∣x1:t−1)=p(x1)t=2∏Np(xt∣xt−1)(p4)
这就是一阶马尔可夫链。这里说的一阶是什么意思?说的 x t x_t xt仅依赖于 x t − 1 x_{t-1} xt−1,如果是二阶,则依赖于 x t − 1 , x t − 2 x_{t-1},x_{t-2} xt−1,xt−2。相当于假设要弱一点,但带来的复杂性也高一点。那最强的假设是什么,朴素贝叶斯假设,所有的 x t x_t xt之间是相互独立的。
前面说概率图模型是概率分布的图形表示,那么它如何表示概率分布呢?
考虑三个变量 a , b , c a,b,c a,b,c的联合分布 p ( a , b , c ) p(a,b,c) p(a,b,c),此时我们不对这些变量做出任何的假设,通过概率的乘积规则,可以将联合概率分布写成:
p ( a , b , c ) = p ( c ∣ a , b ) p ( a , b ) = p ( c ∣ a , b ) p ( b ∣ a ) p ( a ) (p5) p(a,b,c)=p(c|a,b)p(a,b)=p(c|a,b)p(b|a)p(a) \tag{p5} p(a,b,c)=p(c∣a,b)p(a,b)=p(c∣a,b)p(b∣a)p(a)(p5)
此时,我们引入图模型来表示上面等式的右侧。首先我们为每个随机变量引入一个节点,然后为每个节点关联上式右侧对应的条件概率,然后,对于每个条件概率分布,我们在图中添加一个链接(箭头),箭头的起点是条件概率中条件的随机变量对应的节点。结果就是图p2中的图。

可以看到,这个图描述了联合概率分布 p ( a , b , c ) p(a,b,c) p(a,b,c)在所有随机变量上能分解成一组因子的乘积的方式,每个因子只依赖于随机变量的一个子集。
比如对于因子 p ( a ) p(a) p(a),没有输入的链接,也就没有箭头指向它。而对于因子 p ( c ∣ a , b ) p(c|a,b) p(c∣a,b),存在从节点 a , b a,b a,b到节点 c c c的链接。
这里我们说节点 a a a是节点 b b b的父节点,节点 b b b是节点 a a a的子节点。这种关系和数据结构中的图一致。
这里要注意的是,我们隐式地选择了一种顺序来分解 p 5 p5 p5,不同的顺序会对应不同的分解方式,也得到不同的图表示。
我们看到,在图的所有节点上定义的联合概率分布由每个节点上的条件概率分布的乘积表示,每个条件概率分布的条件都是图中节点的父节点所对应的变量。因此,对于一个有 K K K个节点的图,联合概率为:
p ( x ) = ∏ k = 1 K p ( x k ∣ p a k ) (p6) p(\pmb x) = \prod_{k=1}^K p(x_k|pa_k) \tag{p6} p(x)=k=1∏Kp(xk∣pak)(p6)
其中 p a k pa_k pak表示 x K x_K xK的父节点的集合; x = { x 1 , ⋯ , x K } \pmb x=\{x_1,\cdots,x_K\} x={x1,⋯,xK}。这个公式非常重要,表示有向图模型的联合概率的分解(factorization)属性。图中每个节点还可以关联一个变量的集合。
有向图的独立性质
有了这些概念,下面我们来看条件独立相关的图表示,我们以三个变量 a , b , c a,b,c a,b,c的图模型为例。
三个变量 a , b , c a,b,c a,b,c之间的有向图连接对应三个经典的例子,我们先来看第一个。如图p3所示:

根据 ( p 6 ) (p6) (p6),我们可以写出这个图的联合概率分布:
p ( a , b , c ) = p ( c ) p ( a ∣ c ) p ( b ∣ c ) (p7) p(a,b,c) = p(c)p(a|c)p(b|c) \tag{p7} p(a,b,c)=p(c)p(a∣c)p(b∣c)(p7)
该结构为同父结构,即节点 a , b a,b a,b存在相同的父节点 a a a。当父节点 c c c被观测到时, a , b a,b a,b条件独立。
考虑没有变量是观测变量的情形,即我们通过对 ( p 7 ) (p7) (p7)两边进行积分或求和的方式,来考察 a a a和 b b b是否为相互独立的,即
p ( a , b ) = ∑ c p ( c ) p ( a ∣ c ) p ( b ∣ c ) (p8) p(a,b) =\sum_c p(c)p(a|c)p(b|c) \tag{p8} p(a,b)=c∑p(c)p(a∣c)p(b∣c)(p8)
这通常不能分解为乘积 p ( a ) p ( b ) p(a)p(b) p(a)p(b)的形式,因此我们说:
a ⊥̸ b ∣ ∅ a \not \bot \, b \,|\, \empty a⊥b∣∅
这里 ∅ \empty ∅表示空集,符号 ⊥̸ \not \bot ⊥表示条件独立性质不总是成立。
现在假设我们以变量 c c c为条件(或者说观测到变量 c c c,即 c c c取了特定值,不再是一个随机变量),得到的图如p4所示。

我们为上图中的节点添加阴影部分,如节点 c c c所示,表示它被观测到了。
我们可以写成给定 c c c的条件下, a a a和 b b b的条件概率分布,并结合 ( p 7 ) (p7) (p7):
p ( a , b ∣ c ) = p ( a , b , c ) p ( c ) = p ( c ) p ( a ∣ c ) p ( b ∣ c ) p ( c ) = p ( a ∣ c ) p ( b ∣ c ) p(a,b|c) = \frac{p(a,b,c)}{p(c)} = \frac{p(c)p(a|c)p(b|c) }{p(c)} = p(a|c)p(b|c) p(a,b∣c)=p(c)p(a,b,c)=p(c)p(c)p(a∣c)p(b∣c)=p(a∣c)p(b∣c)
因此,我们可以得到条件独立性质(回顾 ( p 3 ) (p3) (p3)):
a ⊥ b ∣ c a \,\bot \,b \,|\, c a⊥b∣c
这里节点 c c c被关于关于从节点 a a a经过节点 c c c到节点 b b b路径的尾到尾(tail-to-tail),因为节点与两个箭头的尾部相连。
这样的一个连接节点 a a a和节点 b b b的路径的存在(从箭头头部到尾部的路径是通的)使得节点相互依赖。
然而,当我们观测到节点 c c c,或者说以 c c c为条件时,被当做条件的节点 c c c阻隔了从 a a a到 b b b的路径,使得 a a a和 b b b变成(条件)独立了。
路径的阻隔表示条件独立!
我们再来看第二个例子,如图p5所示:

该结构称为顺序结构。当 c c c被观测到时, a , b a,b a,b条件独立。
这幅图的联合概率分布通过 ( p 6 ) (p6) (p6)得到,形式为:
p ( a , b , c ) = p ( a ) p ( c ∣ a ) p ( b ∣ c ) (p9) p(a,b,c) = p(a) p(c|a)p(b|c) \tag{p9} p(a,b,c)=p(a)p(c∣a)p(b∣c)(p9)
与之前一样,我们对 c c c积分或求和来考察 a a a和 b b b是否互相独立:
p ( a , b ) = p ( a ) ∑ c p ( c ∣ a ) p ( b ∣ c ) p(a,b) = p(a) \sum_c p(c|a) p(b|c) p(a,b)=p(a)c∑p(c∣a)p(b∣c)
这一般也不能分解为 p ( a ) p ( b ) p(a)p(b) p(a)p(b),因此
a ⊥̸ b ∣ ∅ a \not \bot \, b \,|\, \empty a⊥b∣∅
现在以节点 c c c为条件,再利用公式 ( p 9 ) (p9) (p9):
p ( a , b ∣ c ) = p ( a , b , c ) p ( c ) = p ( a ) p ( c ∣ a ) p ( b ∣ c ) p ( c ) = p ( a , c ) p ( b ∣ c ) p ( c ) = p ( a ∣ c ) p ( b ∣ c ) \begin{aligned} p(a,b|c) &= \frac{p(a,b,c)}{p(c)} \\ &= \frac{p(a) p(c|a)p(b|c)}{p(c)} \\ &= \frac{p(a,c)p(b|c)}{p(c)} \\ &= p(a|c)p(b|c) \end{aligned} p(a,b∣c)=p(c)p(a,b,c)=p(c)p(a)p(c∣a)p(b∣c)=p(c)p(a,c)p(b∣c)=p(a∣c)p(b∣c)
我们再次得到了条件独立性质:
a ⊥ b ∣ c a \,\bot \,b \,|\, c a⊥b∣c
节点 c c c被称为关于从节点 a a a到节点 b b b的路径的头到尾(head-to-tail)。这样的一个连接节点 a a a和节点 b b b的路径的存在使得节点相互依赖。如果我们观测节点 c c c,如图p6所示,这个观测阻隔了从 a a a到 b b b的路径,因此我们得到了条件独立性质。

最后,我们考虑第三个例子,也是最难理解的例子。如图p7所示:

V型结构,也称冲状撞结构。当 c c c未被观测,或者说 c c c未知的情况下, a , b a,b a,b相互独立。当 c c c被观测到, a , b a,b a,b必不独立。
这里提到了给定和未知。基于条件概率 p ( A ∣ B ) p(A|B) p(A∣B),指事件 A A A在事件 B B B已经发生条件下的发生概率。事件 B B B是已经发生的,即给定的、观测到的;事件 A A A的发生是以概率形式表现的, A A A是否发生是未知的。
同样,我们可以得到联合概率分布:
p ( a , b , c ) = p ( a ) p ( b ) p ( c ∣ a , b ) (p10) p(a,b,c)=p(a)p(b)p(c|a,b) \tag{p10} p(a,b,c)=p(a)p(b)p(c∣a,b)(p10)
对上式两侧关于 c c c积分或求和,得到:
p ( a , b ) = p ( a ) p ( b ) p(a,b)=p(a)p(b) p(a,b)=p(a)p(b)
因为 p ( c ∣ a , b ) p(c|a,b) p(c∣a,b)是关于 c c c的条件分布,也是一种概率分布,对 c c c求和或积分结果为 1 1 1。
这样,我们得到了和之前不一样的结果,当没有变量被观测时, a a a和 b b b是独立的。我们可以把这个结果写成:
a ⊥ b ∣ ∅ a \,\bot \,b \,|\, \empty a⊥b∣∅

那么,假设我们还是以 c c c为条件,如图p8所示,有:
p ( a , b ∣ c ) = p ( a , b , c ) p ( c ) = p ( a ) p ( b ) p ( c ∣ a , b ) p ( c ) p(a,b|c) = \frac{p(a,b,c)}{p(c)} = \frac{p(a)p(b)p(c|a,b)}{p(c)} p(a,b∣c)=p(c)p(a,b,c)=p(c)p(a)p(b)p(c∣a,b)
这通常也不能分解为 p ( a ) p ( b ) p(a)p(b) p(a)p(b),因此,
a ⊥̸ b ∣ c a \,\not \bot \,b \,|\, c a⊥b∣c
图形上来看,我们说节点 c c c关于从 a a a到 b b b的路径是头到头(head-to-head)。当 c c c没有被观测到时,它阻隔了路径,使得变量 a a a和 b b b是相互独立的。当以 c c c为条件时,路径被解除阻隔,使得 a a a和 b b b相互依赖了。
特别地,我们考虑下图p9这种情形。是V型结构的延伸,其中新节点 d d d是节点 c c c的孩子节点,但该结构中仅 d d d被观测到,那么 a a a和 b b b也会被解除阻隔。其实,不仅是 c c c的直接孩子节点 d d d,当 c c c或 c c c的任意后继(descendant)节点被观测到,都会使得 a a a和 b b b解除阻隔。

怎么证明呢?
我们还是先写出概率分布:
p ( a , b , c , d ) = p ( a ) p ( b ) p ( c ∣ a , b ) p ( d ∣ c ) p(a,b,c,d) = p(a)p(b)p(c|a,b)p(d|c) p(a,b,c,d)=p(a)p(b)p(c∣a,b)p(d∣c)
假设观测到 d d d,我们考虑 a , b a,b a,b是否是条件独立的。
p ( a , b ∣ d ) = ∑ c p ( a , b , c ∣ d ) = ∑ c p ( a , b , c , d ) p ( d ) = ∑ c p ( a ) p ( b ) p ( c ∣ a , b ) p ( d ∣ c ) p ( d ) = ∑ c p ( a ) p ( b ) p ( c ∣ a , b ) p ( d ∣ c , a , b ) p ( d ) = ∑ c p ( a ) p ( b ) p ( d , c ∣ a , b ) p ( d ) = p ( a ) p ( b ) p ( d ∣ a , b ) p ( d ) ≠ p ( a ) p ( b ) \begin{aligned} p(a,b|d) &= \sum_c p(a,b,c|d) \\ &= \sum_c \frac{p(a,b,c,d)}{p(d)} \\ &= \sum_c \frac{ p(a)p(b)p(c|a,b)p(d|c)}{p(d)} \\ &= \sum_c \frac{ p(a)p(b)p(c|a,b)p(d|c,a,b)}{p(d)} \\ &= \sum_c \frac{ p(a)p(b)p(d,c|a,b)}{p(d)} \\ &= \frac{ p(a)p(b)p(d|a,b)}{p(d)} \\ &\neq p(a)p(b) \end{aligned} p(a,b∣d)=c∑p(a,b,c∣d)=c∑p(d)p(a,b,c,d)=c∑p(d)p(a)p(b)p(c∣a,b)p(d∣c)=c∑p(d)p(a)p(b)p(c∣a,b)p(d∣c,a,b)=c∑p(d)p(a)p(b)p(d,c∣a,b)=p(d)p(a)p(b)p(d∣a,b)=p(a)p(b)
这里用到了 d , c , a d,c,a d,c,a和 d , c , b d,c,b d,c,b满足上面描述的顺序结构,即 p ( d ∣ a , b , c ) = p ( d ∣ c ) p(d|a,b,c)=p(d|c) p(d∣a,b,c)=p(d∣c)。
我们再考虑相反的情况,假设未观测到 d d d,有:
p ( a , b , c , d ) = p ( a ) p ( b ) p ( c ∣ a , b ) p ( d ∣ c ) p(a,b,c,d)= p(a)p(b)p(c|a,b)p(d|c) p(a,b,c,d)=p(a)p(b)p(c∣a,b)p(d∣c)
对上式两侧关于 d d d积分或求和,得到:
p ( a , b , c ) = p ( a ) p ( b ) p ( c ∣ a , b ) p(a,b,c) = p(a)p(b)p(c|a,b) p(a,b,c)=p(a)p(b)p(c∣a,b)
再关于 c c c积分或求和:
p ( a , b ) = p ( a ) p ( b ) p(a,b)=p(a)p(b) p(a,b)=p(a)p(b)
同样,当没有变量被观测到时有:
a ⊥ b ∣ ∅ a \,\bot \,b \,|\, \empty a⊥b∣∅
可以看到在未观测到 d d d的情况下, a , b a,b a,b还是互相独立的。这和节点 c c c的性质是一样的。反之,在观测到 d d d的情况下,联合概率不能分解成 p ( a ) p ( b ) p(a)p(b) p(a)p(b)。
我们可以以一个例子来简单理解,假设你家装了一个偷窃报警器,当家里遭窃或地震都有可能触发这个偷窃报警器响,而当报警器响的情况下,邻居听到后可能给你打电话。

地震与否不会被你家是否遭窃影响。这里也假设小偷不管有没有地震,都不影响他进行偷窃。此时,这两个事件在报警响未被观测到的情况下,就是独立的。
假设你正在外度假,邻居给你打电话说你家报警器响了。那么从邻居打电话这个事件我们可以得到警报响这个事件发生了。
最后,我们总结成一个图:

再重申一次,若 a a a到 b b b的路径被阻隔,说明它们是(条件)独立的。
基于上面的三个例子,下面我们引入一个非常重要的概念D-划分(D-Separation),也称为有向分离,或D-分离。
D-划分
图模型的一个重要且优雅的特征是,联合概率分布的条件独立性可以直接从图中读出来,不用进行任何计算。完成这件事的一般框架就是d-划分,d表示有向。
考虑一个一般的有向图,其中 A , B , C A,B,C A,B,C是任意无交集的节点集合。我们考虑从 A A A中任意节点到 B B B中任意节点的所有可能的路径,我们说这样的路径被阻隔,如果它包含一个节点满足下面两个性质中的任意一个:
- 路径上的箭头以头到尾或尾到尾的方式交汇于这个节点,且这个节点在集合 C C C中;
- 箭头以头到头的方式交汇于这个节点,且这个节点和它的所有后继都不在集合 C C C中;
如果所有的路径都被阻隔,我们说 C C C把 A A A从 B B B中d-划分开,且图中所有变量上的联合概率分布都满足 A ⊥ B ∣ C A \, \bot \, B \, | \, C A⊥B∣C。

如图p12所示。尾到尾是红线表示,头到尾是黑线表示,都交汇于集合 C C C中;而头到头方式交汇的节点,不在集合 C C C中。
我们再通过一个例子来理解一下,例子来自PRML。

在p13左图中,从 a a a到 b b b的路径是通的,首先对于 a → e → f a \rightarrow e \rightarrow f a→e→f的路径,这是一个头到头结构,虽然 e e e未被观测到,但 e e e的后继 c c c被观测到,因此这条路径是通的,然后对于 e → f → b e \rightarrow f \rightarrow b e→f→b的路径,这是尾到尾结构,且 f f f没有被观测到,没有被 f f f阻隔;
在p13右图中,从 a a a到 b b b的路径被节点 e e e和 f f f阻隔,对于 a → e → f a \rightarrow e \rightarrow f a→e→f的路径, e e e和 e e e的后继没有被观测到(没有在条件集合中), a a a到 f f f是被阻隔的;同时对于 e → f → b e \rightarrow f \rightarrow b e→f→b来说,是一个尾到尾结构,且 f f f被观测到。因此使用这幅图进行分解的任何概率分布都满足条件独立性质 a ⊥ b ∣ f a \, \bot \, b \, | \, f a⊥b∣f。
下面我们来看如何用概率图来表示隐马尔科夫模型。
隐马尔可夫模型图示
假设针对顺序观测数据,基于一阶马尔可夫假设,即每个观测只与最近的一次观测有关,我们就得到了一阶马尔科夫链(马尔科夫模型), N N N次观测的序列的联合分布为:
p ( x 1 : N ) = p ( x 1 ) ∏ t = 2 N p ( x t ∣ x 1 : t − 1 ) = p ( x 1 ) ∏ t = 2 N p ( x t ∣ x t − 1 ) p(x_{1:N})=p(x_1)\prod_{t=2}^N p(x_t|x_{1:t-1}) = p(x_1)\prod _{t=2}^N p(x_t|x_{t-1}) p(x1:N)=p(x1)t=2∏Np(xt∣x1:t−1)=p(x1)t=2∏Np(xt∣xt−1)
该一阶马尔可夫链用概率图表示如图p14所示:

再进一步,如果引入额外的潜在变量 z n z_n zn,假设潜在变量也构成了马尔可夫链,得到的图结构称为状态空间结构(state space model),如图p15所示。它满足下面的条件独立性质,即在给定 z n z_n zn的条件下, z n − 1 z_{n-1} zn−1和 z n + 1 z_{n+1} zn+1是独立的,有:
z n + 1 ⊥ z n − 1 ∣ z n (p11) z_{n+1} \, \bot \, z_{n-1}\, | \,z_n \tag{p11} zn+1⊥zn−1∣zn(p11)

这个模型的联合概率分布为
p ( x 1 , ⋯ , x N , z 1 , ⋯ , z N ) = p ( z 1 ) [ ∏ t = 2 N p ( z t ∣ z t − 1 ) ] ∏ t = 1 N p ( x t ∣ z t ) (p12) p(x_1,\cdots,x_N,z_1,\cdots,z_N) = p(z_1)\left[\prod_{t=2}^N p(z_t|z_{t-1}) \right] \prod_{t=1}^N p(x_t|z_t) \tag{p12} p(x1,⋯,xN,z1,⋯,zN)=p(z1)[t=2∏Np(zt∣zt−1)]t=1∏Np(xt∣zt)(p12)
根据d-划分准则,我们看到总存在一个路径通过潜在变量连接了任意两个观测变量 x n x_n xn和 x m x_m xm,并且这个路径永远不会被阻隔。对于观测变量 x n + 1 x_{n+1} xn+1来说,给定所有之间的观测,条件概率分布 p ( x n + 1 ∣ x 1 : n ) p(x_{n+1}|x_{1:n}) p(xn+1∣x1:n)不会表现出任何的条件独立性,因为对 x n + 1 x_{n+1} xn+1的预测依赖于所有之前的观测。
对于顺序数据来说,如果潜在变量是离散的,那么这个图描述的就是隐马尔可夫模型。
隐马尔可夫模型的基本概念
隐马尔可夫模型的定义
定义 10.1(隐马尔可夫模型) 隐马尔可夫模型是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列(状态序列,state sequence),然后由每个状态生成一个观测从而产生随机观测序列(observation sequence)的过程。序列的每一个位置又可以看作是一个时刻。
隐马尔可夫模型由初始概率分布、状态转移概率分布以及观测概率分布确定,模型概率图示如图1所示,模型的形式定义为:

设 Q Q Q是所有可能的状态的集合, V V V是所有可能的观测的集合:
Q = { q 1 , q 2 , ⋯ , q N } , V = { v 1 , v 2 , ⋯ , v M } Q=\{q_1,q_2,\cdots,q_N\},\qquad V=\{v_1,v_2,\cdots,v_M\} Q={q1,q2,⋯,qN},V={v1,v2,⋯,vM}
其中 N N N是可能的状态数, M M M是可能的观测数。
I I I是长度为 T T T的状态序列, O O O是对应的观测序列,由于一个状态生成一个观测,所以它们的长度是相同的:
I = ( i 1 , i 2 , ⋯ , i T ) , O = ( o 1 , o 2 , ⋯ , o T ) I=(i_1,i_2,\cdots,i_T),\qquad O=(o_1,o_2,\cdots,o_T) I=(i1,i2,⋯,iT),O=(o1,o2,⋯,oT)
A A A是状态转移概率矩阵:
A = [ a i j ] N × N (10.1) A=[a_{ij}]_{N\times N} \tag{10.1} A=[aij]N×N(10.1)
其中,
a i j = P ( i t + 1 = q j ∣ i t = q i ) , i = 1 , 2 , ⋯ , N ; j = 1 , 2 , ⋯ , N (10.2) a_{ij} = P(i_{t+1}=q_j|i_t=q_i),\quad i=1,2,\cdots,N;\quad j=1,2,\cdots,N \tag{10.2} aij=P(it+1=qj∣it=qi),i=1,2,⋯,N;j=1,2,⋯,N(10.2)
表示时刻 t t t处于状态 q i q_i qi的条件下,在时刻 t + 1 t+1 t+1转移到状态 q j q_j qj的概率。
B B B是观测概率矩阵:
B = [ b j ( k ) ] N × M (10.3) B=[b_j(k)]_{N \times M} \tag{10.3} B=[bj(k)]N×M(10.3)
其中,
b j ( k ) = P ( o t = v k ∣ i t = q j ) , k = 1 , 2 , ⋯ , M ; j = 1 , 2 , ⋯ , N (10.4) b_j(k) = P(o_t=v_k|i_t=q_j),\quad k=1,2,\cdots,M;\quad j=1,2,\cdots,N \tag{10.4} bj(k)=P(ot=vk∣it=qj),k=1,2,⋯,M;j=1,2,⋯,N(10.4)
这个表示可能不好理解,类似 a i j a_{ij} aij,下标表示状态,那么这里用括号表示观测。
表示时刻 t t t处于状态 q j q_j qj的条件下,生成观测 v k v_k vk的概率。 b j ( k ) b_j(k) bj(k)只涉及到当前时刻 t t t。
π \pi π是初始状态概率向量:
π = ( π i ) (10.5) \pi = (\pi_i) \tag{10.5} π=(πi)(10.5)
其中,
π i = P ( i 1 = q i ) , i = 1 , 2 , ⋯ , N (10.6) \pi_i = P(i_1=q_i),\quad i=1,2,\cdots,N \tag{10.6} πi=P(i1=qi),i=1,2,⋯,N(10.6)
还是用下标表示状态,但符号变成了 π \pi π,表示时刻 t = 1 t=1 t=1处于状态 q i q_i qi的概率,所以是初始概率。
上面的符号有点多,记不住没关系,后面碰到的时候多回顾几次就好了。
HMM由初始状态概率向量 π \pi π、状态转移概率矩阵 A A A和观测概率矩阵 B B B决定。 π \pi π和 A A A决定状态序列, B B B决定观测序列。因此,隐马尔可夫模型 λ \lambda λ可用三元符号表示,
λ = ( A , B , π ) (10.7) \lambda=(A,B,\pi) \tag{10.7} λ=(A,B,π)(10.7)
A , B , π A,B,\pi A,B,π称为隐马尔可夫模型的三要素。
A和 π \pi π确定了隐藏的马尔可夫链,生成不可观测的状态序列。观测概率矩阵 B B B确定了如何从状态生成观测。
从定义可知,隐马尔可夫模型作了两个基本假设:
(1) 齐次马尔可夫性假设,即假设隐藏的马尔可夫链在任意时刻 t t t的状态只依赖于其前一时刻的状态,与其他时刻的状态及观测无关,也与时刻 t t t无关:
P ( i t ∣ i t − 1 , o t − 1 , ⋯ , i 1 , o 1 ) = P ( i t ∣ i t − 1 ) , t = 1 , 2 , ⋯ , T (10.8) P(i_t|i_{t-1},o_{t-1},\cdots,i_1,o_1) = P(i_t|i_{t-1}),\quad t=1,2,\cdots,T \tag{10.8} P(it∣it−1,ot−1,⋯,i1,o1)=P(it∣it−1),t=1,2,⋯,T(10.8)
齐次指的是,任何时刻的状态转移概率与时刻 t t t无关,都是一样的。
(2) 观测独立假设,即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态,与其他观测及状态无关:
P ( o t ∣ i T , o T , i T − 1 , o T − 1 , ⋯ , i t + 1 , o t + 1 , i t , i t − 1 , o t − 1 , ⋯ , i 1 , o 1 ) = P ( o t ∣ i t ) (10.9) P(o_t|i_T,o_T,i_{T-1},o_{T-1},\cdots,i_{t+1},o_{t+1},i_t,i_{t-1},o_{t-1},\cdots,i_1,o_1) = P(o_t|i_t) \tag{10.9} P(ot∣iT,oT,iT−1,oT−1,⋯,it+1,ot+1,it,it−1,ot−1,⋯,i1,o1)=P(ot∣it)(10.9)
隐马尔可夫模型可用于标注,此时状态就对应要标注的标签(标记)。标注问题的标记是隐藏的、未知的,已知的是观测到的(单词)序列。
例 10.1(盒子和球模型) 假设有4个盒子,每个盒子里都装有红、白两种颜色的球。该例子主要是描述了初始概率分布 π \pi π,状态转移概率分布 A A A和观测概率分布 B B B。具体可以查阅书上的内容。
观测序列的生成过程
可以将一个长度为 T T T的观测序列 O = ( o 1 , o 2 , ⋯ , o T ) O=(o_1,o_2,\cdots,o_T) O=(o1,o2,⋯,oT)的生成过程描述如下。
算法10.1(观测序列的生成)
输入:隐马尔可夫模型 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π),观测序列长度 T T T;
输出:观测序列 O = ( o 1 , o 2 , ⋯ , o T ) O=(o_1,o_2,\cdots,o_T) O=(o1,o2,⋯,oT)。
(1) 安装初始状态分布 π \pi π产生状态 i 1 i_1 i1;
(2) 令 t = 1 t=1 t=1;
(3) 按照状态 i t i_t it的观测概率分布 b i t ( k ) b_{i_t}(k) bit(k)生成 o t = v k o_t=v_k ot=vk;
(4) 按照状态 i t i_t it的状态转移概率分布 { a i t , i t + 1 } \{a_{i_t,i_{t+1}}\} {ait,it+1}产生状态 i t + 1 i_{t+1} it+1;
(5) 令 t = t + 1 t=t+1 t=t+1;如果 t < T t < T t<T,转步(3);否则,终止。
隐马尔可夫模型的3个基本问题
隐马尔可夫模型由3个基本问题:
(1) 概率计算问题。给定模型 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π)和观测序列 O = ( o 1 , o 2 , ⋯ , o T ) O=(o_1,o_2,\cdots,o_T) O=(o1,o2,⋯,oT),计算在模型 λ \lambda λ下观测序列 O O O出现的概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)。
(2) 学习问题。已知观测序列 O = ( o 1 , o 2 , ⋯ , o T ) O=(o_1,o_2,\cdots,o_T) O=(o1,o2,⋯,oT),估计模型 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π)参数,使得在该模型下观测序列概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)最大。即用极大似然估计法估计参数。
(3) 预测问题,也称为解码问题。已知模型 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π)和观测序列 O = ( o 1 , o 2 , ⋯ , o T ) O=(o_1,o_2,\cdots,o_T) O=(o1,o2,⋯,oT),求对给定观测序列条件概率 P ( I ∣ O ) P(I|O) P(I∣O)最大的状态序列 I = ( i 1 , i 2 , ⋯ , i T ) I=(i_1,i_2,\cdots,i_T) I=(i1,i2,⋯,iT)。即给定观测序列,求对应的最有可能的状态序列。
相关文章:

《统计学习方法》——隐马尔可夫模型(上)
引言 这是《统计学习方法》第二版的读书笔记,由于包含书上所有公式的推导和大量的图示,因此文章较长,正文分成三篇,以及课后习题解答,在习题解答中用Numpy实现了维特比算法和前向后向算法。 《统计学习方法》——隐马…...

ElasticSearch删除索引【真实案例】
文章目录 背景分析解决遇到的问题 - 删除超时报错信息解决办法1:调大超时时间解决办法2:调大ES堆内存参考背景 项目中使用了ELK技术栈实现了日志管理,但是日志管理功能目前并没有在生产上实际使用。 但ELK程序依然在运行,导致系统磁盘发生告警,剩余可用磁盘不足10%。 所以…...

基于FPGA+JESD204B 时钟双通道 6.4GSPS 高速数据采集设计(三)连续多段触发存储及传输逻辑设计
本章将完成数据速率为 80MHz 、位宽为 12bits 的 80 路并行采样数据的连续多 段触发存储。首先,给出数据触发存储的整体框架及功能模块划分。然后,简介 MIG 用户接口、设置及读写时序。最后,进行数据跨时钟域模块设计,内存…...

对 Iterator, Generator 的理解?
Iterator Iterator是最简单最好理解的。 简单的说,我们常用的 for of 循环,都是通过调用被循环对象的一个特殊函数 Iterator 来实现的,但是以前这个函数是隐藏的我们无法访问, 从 Symbol 引入之后,我们就可以通过 Sy…...

C++基础
文章目录 C命名空间定义命名空间using指令不连续的命名空间嵌套的命名空间 面向对象类类成员的访问权限及类的封装对象类成员函数类访问修饰符构造函数和析构函数类的构造函数带参数的构造函数使用初始化列表来初始化字段类的析构函数拷贝构造函数 友元函数内联函数this指针指向…...

软件测试全流程
软件测试全流程 一、制定测试策略二、制定测试方案三、编辑测试用例四、执行测试用例五、输出问题单六、回归测试七、测试文件归档 一、制定测试策略 1、测试目的测试范围 2、用什么测试方法工具(例如功能测试用黑盒测试) 3、测试优先级(功能…...
【软件测试】支付模块测试攻略,这些测试方法和注意事项你掌握了么?
对于大部分人而言,支付模块或许是日常生活中最为关注和使用的功能之一,因此,对于支付模块的质量控制也显得尤为重要。 但考虑到支付涉及到金钱流转等敏感信息,一旦出现问题可能带来非常严重后果。因此,在支付模块测试…...

刷完这个笔记,17K不能再少了....
大家好,最近有不少小伙伴在后台留言,得准备面试了,又不知道从何下手!为了帮大家节约时间,特意准备了一份面试相关的资料,内容非常的全面,真的可以好好补一补,希望大家在都能拿到理想…...

知识变现创业指南-《知识变现秘籍》
《知识变现秘籍》 知识变现创业者指南 读完将改变你的认知 开阔你的知识变现思路 系统掌握知识变现的要点 知识付费创业方法 帮你利用知识赚到你弟一桶金 如果你有一技之长,想变现 如果你有一身才华,想变现 如果你在某个领域有绝活 如果你是&am…...
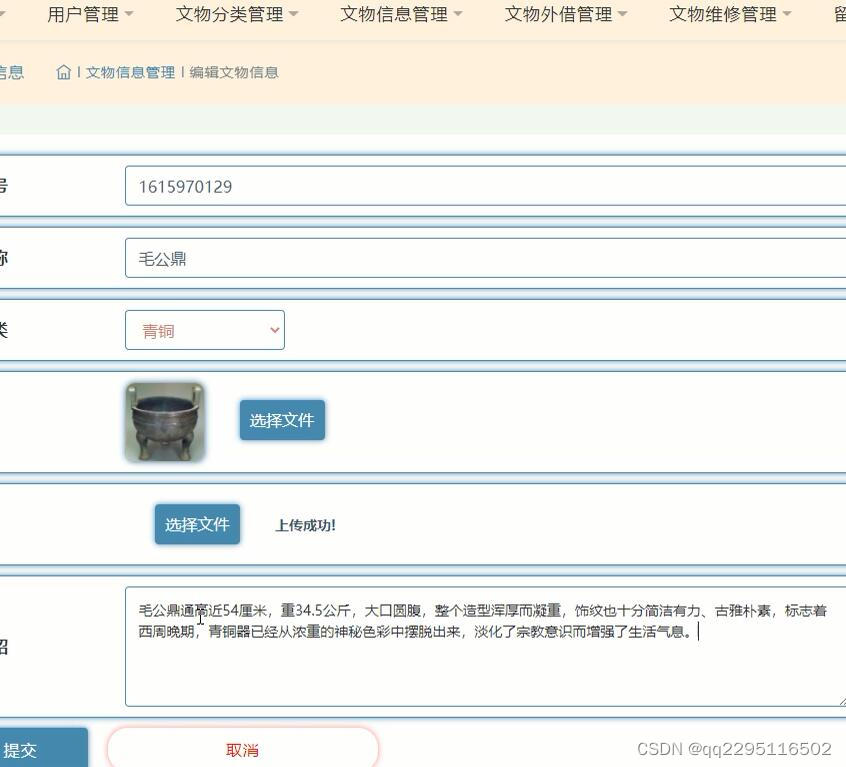
springboot+java博物馆文物管理系统
用户前台进入系统可以进行首页、文物信息、论坛交流、文物资讯、留言反馈、我的、跳转到后台等springboot是基于spring的快速开发框架, 相比于原生的spring而言, 它通过大量的java config来避免了大量的xml文件, 只需要简单的生成器便能生成一个可以运行的javaweb项目, 是目前最…...
——Ansible 的脚本(playbook 剧本))
Ansible 自动化运维工具(二)——Ansible 的脚本(playbook 剧本)
Ansible 自动化运维工具—Ansible 的脚本playbook 剧本 playbooks 概述以及实例操作playbooks 的组成操作示例一:编写yaml文件也就是playbook修改配置文件并放入/opt/目录下运行playbook 操作实例二:定义、引用变量操作示例三:指定远程主机su…...
阿里云镜像服务下载并安装Go环境
【阿里云镜像】下载并安装Go环境 一、参考链接 阿里巴巴开源镜像站-OPSX镜像站-阿里云开发者社区 (aliyun.com) golang镜像-golang下载地址-golang安装教程-阿里巴巴开源镜像站 (aliyun.com) GO语言安装以及国内镜像 - DbWong_0918 - 博客园 (cnblogs.com) 二、Go介绍 Gol…...

工作线程快速优雅退出方式探讨
本文我们不用定时器。定时器会阻塞消息循环。先看需求: 我们先看第一种,有一个任务,要求每1秒钟执行一次,最常见的写法如下两种 bool bExitThread false; DWORD WorkThread1(LPVOID param) {while (false bExitThread){//// to…...
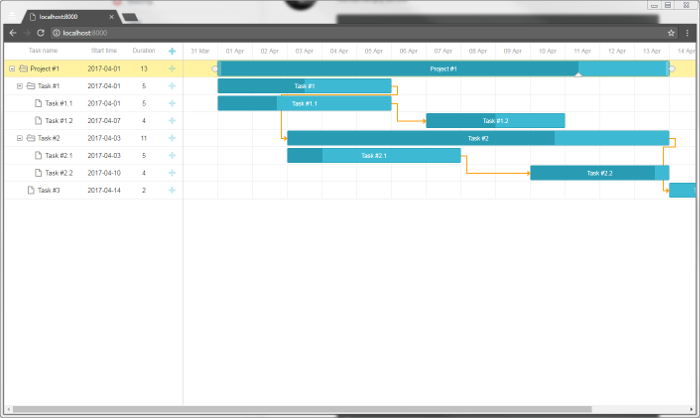
甘特图控件DHTMLX Gantt教程:用PHP:Laravel实现Gantt(上)
DHTMLX Gantt是用于跨浏览器和跨平台应用程序的功能齐全的Gantt图表。可满足项目管理应用程序的大部分开发需求,具备完善的甘特图图表库,功能强大,价格便宜,提供丰富而灵活的JavaScript API接口,与各种服务器端技术&am…...

ffmpeg-命令大全03
ffplay/mpv 查看所有的解码器 ffplay -decoders >>decoders.txt ffplay无延时无缓存播放 ffplay -fflags nobuffer -i "%1" ffplay指定size播放 ffplay -x 480 -y 270 -i "%1" ffplay指定解码器 ffplay -vcodec hevc_cuvid "%1" […...

MATLAB中太赫兹时域光谱的最大似然参数估计
目录 一、引言 二、最大似然估计的基本原理 三、MATLAB中的最大似然估计实现 四、太赫兹时域光谱的最大似然参数估计 五、结论 六、参考文献 一、引言 太赫兹波(Terahertz wave)是电磁谱中介于微波与光波之间的一段频率范围,频率大约在…...
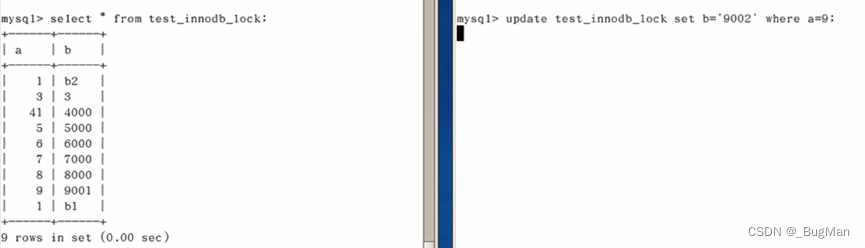
详解MySQL的并发控制
目录 1.概述 2.事务 2.1.什么是事务 2.2.事务的隔离级别 2.2.1.三种数据一致性问题 2.2.2.四种隔离级别 2.3.如何设置隔离级别 3.锁 3.1.锁与事务的关系 3.2.分类 3.3.表锁 3.3.1.概述 3.3.2.读锁 3.3.3.写锁 3.3.4.保护机制 3.4.行锁 3.4.1.概述 3.4.2.什么…...

Android Termux安装MySQL数据库 | 公网安全远程连接【cpolar内网穿透】
文章目录 前言1.安装MariaDB2.安装cpolar内网穿透工具3. 创建安全隧道映射mysql4. 公网远程连接5. 固定远程连接地址 前言 Android作为移动设备,尽管最初并非设计为服务器,但是随着技术的进步我们可以将Android配置为生产力工具,变成一个随身…...

SpringBoot的常见配置
SpringBoot基础配置 1. 配置文件格式问题导入1.1 修改服务器端口1.2 自动提示功能消失解决方案1.3 SpringBoot配置文件加载顺序 2. yaml问题导入2.1 yaml语法规则2.2 yaml数组数据2.3 yaml数据读取 3. 多环境开发配置问题导入3.1 多环境启动配置3.2 多环境启动命令格式3.3 多环…...
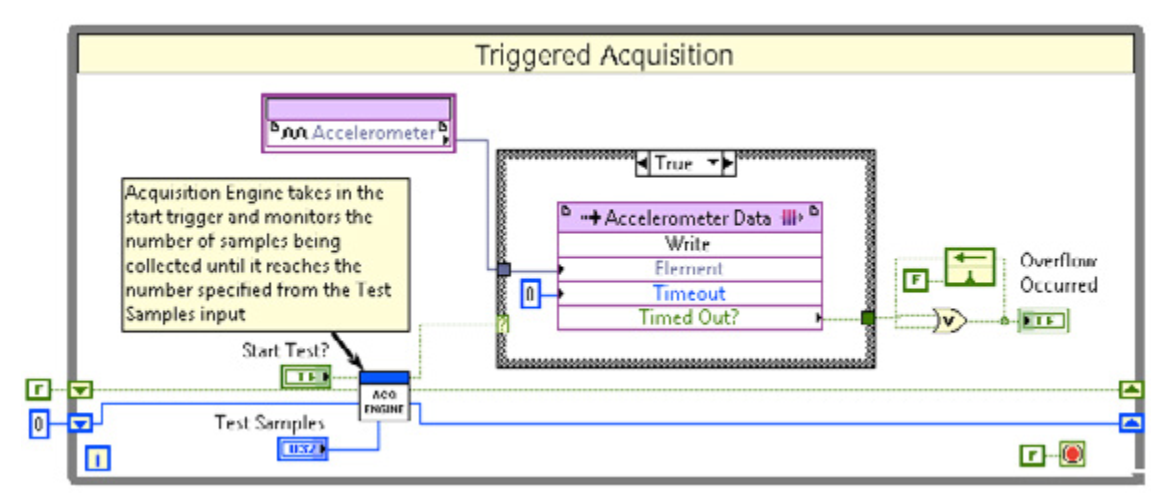
LabVIEWCompactRIO 开发指南25 实施LabVIEW FPGA代码的方法
LabVIEWCompactRIO 开发指南25 实施LabVIEW FPGA代码的方法 开始开发时,应在LabVIEW项目的FPGA目标下创建VI,以便使用LabVIEW FPGA选板进行编程,该选板是LabVIEW选板的子集,包括一些LabVIEW FPGA特定函数。 应该在仿真模式下开…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
