每日练习---C语言
目录
前言:
1.打印菱形
1.1补充练习
2.打印水仙花
2.1补充训练
前言:
记录博主做题的收获,以及提升自己的代码能力,今天写的题目是:打印菱形、打印水仙花数。
1.打印菱形
我们先看到牛客网的题:OJ链接
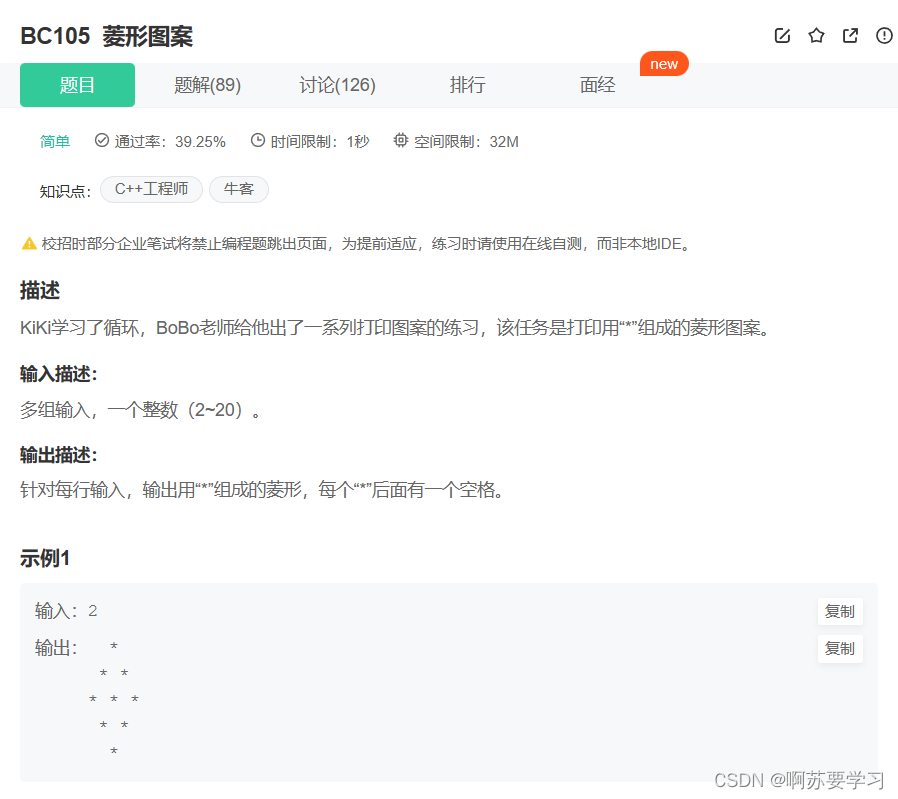
题目解析:多组输入一个值(我们用n来控制)用来控制菱形的打印。
思路:将最长一行的之上的看成是上半部分,包括最长一行在内的之下划为下半部分;上部分是n行,有n列,每一列由空格和星号组成,空格减少,星号增多;下半部分是n+1行,有n+1列,空格增多,星号减少;
#include <stdio.h>int main()
{int n = 0;//1.多组输入while(scanf("%d", &n) != EOF){//i控制行int i = 0;//2.打印上半部分for(i = 0; i < n; i++){int j = 0;//2.1打印对应行的空格列for(j = 0; j < n - i; j++){printf(" ");}//2.2打印对应行的星号列for(j = 0; j <= i; j++){printf("* ");}printf("\n");//一列打印完换行}//3.打印下半部分for(i = 0; i < n + 1; i++){int j = 0;for(j = 0; j < i; j++){printf(" ");}for(j = 0; j < n + 1 - i; j++){printf("* ");}printf("\n");}}return 0;
}1.1补充练习
打印出下面的图案:

还是一样的思路,分为上半部分和下半部分,上面有6行,那我们输入的时候就把n输进去一个6,下半部分是7行,也就是n+1。
#include <stdio.h>int main()
{int n = 0;scanf("%d", &n);int i = 0;for(i = 0; i < n; i++){int j = 0;for(j = 0; j < n - i; j++){//看图会发现是两个空格printf(" ");}//第一次是1个,后面每次增加2//i一开是为0,没往下一行,就多打印两个*for(j = 0; j < 1 + 2 * i; j++){printf("* ");}printf("\n");}for(i = 0; i < n + 1; i++){int j = 0;for(j = 0; j < i; j++){printf(" ");}//7行打印13个 2*n+2是14,减去1等于13,刚好//对于下半部分,第一行i为0不减,没往下一行,就多减2个星号的打印for(j = 0; j < 2*n + 2 - 1 - 2*i; j++){printf("* ");}printf("\n");}return 0;
}
相信看完后,读者对循环的掌控可以更如鱼得水一点~
2.打印水仙花
水仙花数的定义:有一个n位数,它的每一位数的n次方之和等于它本身。例如153这个数字:153 = 1^3 + 5^3 + 3^3 = 1 + 125 + 27。
我们先看到牛客网的题:OJ链接

题目的意思是说:多组输入两个整数m和n;输出在m和n范围内的水仙花数,并且用空格隔开。水仙花在范围内[m,n],我们遍历的时候,是就打印,不是就跳过,水仙化数自然是从小到大排列的。
#include <stdio.h>
#include <math.h>int main()
{int m, n;int flag = 1;//1.多组输入while(scanf("%d%d", &m, &n) != EOF){//2.创建i,并用i遍历区间[m,n]int i = 0;for(i = m; i <= n; i++){//3.用k当做i的副本使用,不要在循环内改变循环变量iint k = i;int sum = 0;while(k){//题目已知是三位数,用3直接当做次方sum += pow(k%10, 3);k /= 10;}//4.如果加起来的sum等于i,就是水仙花数if(sum == i){printf("%d ", i);//有打印,就把flag改成0flag = 0;}}//5.如果全部遍历完,没有打印出一个水仙花,flag没有被改成0//就在这里打印出noif(flag){printf("no");}}
}解释:看到第3步骤,假设k是123,进入循环,k取模上10得到3,pow(3, 3)是3的3次方,然后k /= 10,123除以10商12,把12赋值给了k;接着循环,直到k /= 10把商为0赋值给k,循环结束。
补充:注意sum要定义在for循环内,不能定义在for循环外,这样sum在每次重新判断一个数是不是水仙数的时候,都会带着上次求的sum值。或者定义在外面,每次for循环重新赋值成0。
2.1补充训练
打印0-100000(十万)之间的水仙花数。
#include <stdio.h>
#include <stdio.h>int main()
{int i = 0;for(i = 0; i < 100000; i++){//1.求i的几位数的int n = 1;int m = i;while(m/=10){n++}//2.求每一位数的n次阶乘之和m = i;int sum = 0;while(m){sum = pow(m%10, n);m /= 10;}//3.判断sum等不等于iif(sum == i){printf("%d ", i);}}return 0;
}解释:求i是几位数的时候,n从1开始是因为,假设我们此时i是12,m被初始化为12,m/10会以1的值进入循环,并被赋值成1,然后n++一次;接着m/10为商0余1,进不去循环了,如果一开始我们的n是从0开始的,那么只经过一次n++,n为1,实际上i是两位数;所以n一开始设成1,这是因为无论是什么数,一开始都有一位数。
总结:多组输入的方法、控制循环的训练、将一个整数一个一个剥离下来的方法、以及锻炼手敲代码的能力和不怕出错进行调试的抗压心态。
希望大家读完,可以自己找到题目实现一遍,祝读者们有所收获。(喜欢的话麻烦留个小赞再走呗)!
相关文章:

每日练习---C语言
目录 前言: 1.打印菱形 1.1补充练习 2.打印水仙花 2.1补充训练 前言: 记录博主做题的收获,以及提升自己的代码能力,今天写的题目是:打印菱形、打印水仙花数。 1.打印菱形 我们先看到牛客网的题:OJ链…...

边缘计算如何推动物联网的发展
随着物联网(IoT)的快速发展,物联网设备数量呈现爆炸性增长,这给网络带来了巨大的压力和挑战。边缘计算作为一种新兴的计算模式,旨在解决数据处理和通信在网络传输中的延迟和带宽限制问题,从而提高数据处理效…...

第五章 栈与队列
目录 一、用栈实现队列二、用队列实现栈三、有效的括号四、删除字符串中的所有相邻重复项五、逆波兰表达式求值六、滑动窗口最大值七、前 K 个高频元素 一、用栈实现队列 Leetcode 232 class MyQueue { public:stack<int> in, out;MyQueue() {}void push(int x) {in.pu…...

PyQt5桌面应用开发(16):定制化控件-QPainter绘图
本文目录 PyQt5桌面应用系列画画图,喝喝茶QPainter和QPixmapQPixmapQPainter绘制事件 一个魔改的QLabelCanvas类主窗口主程序: 总结 PyQt5桌面应用系列 PyQt5桌面应用开发(1):需求分析 PyQt5桌面应用开发(2…...

spring5源码篇(9)——mybatis-spring整合原理
spring-framework 版本:v5.3.19 spring和mybatis的整合无非主要就是以下几个方面: 1、SqlSessionFactory怎么注入? 2、Mapper代理怎么注入? 3、为什么要接管mybatis事务? 文章目录 一、SqlSessionFactory怎么注入SqlSe…...

为什么需要防雷接地,防雷接地的作用是什么
为什么需要电气接地? 您是否曾经在工作条件下使用任何电器时接触过电击?几乎每个人的答案都是肯定的,有时这些电击是轻微的,但有时会对电气和电子设备造成损坏,并可能危及生命。为防止对人的生命和电器造成任何损害&a…...
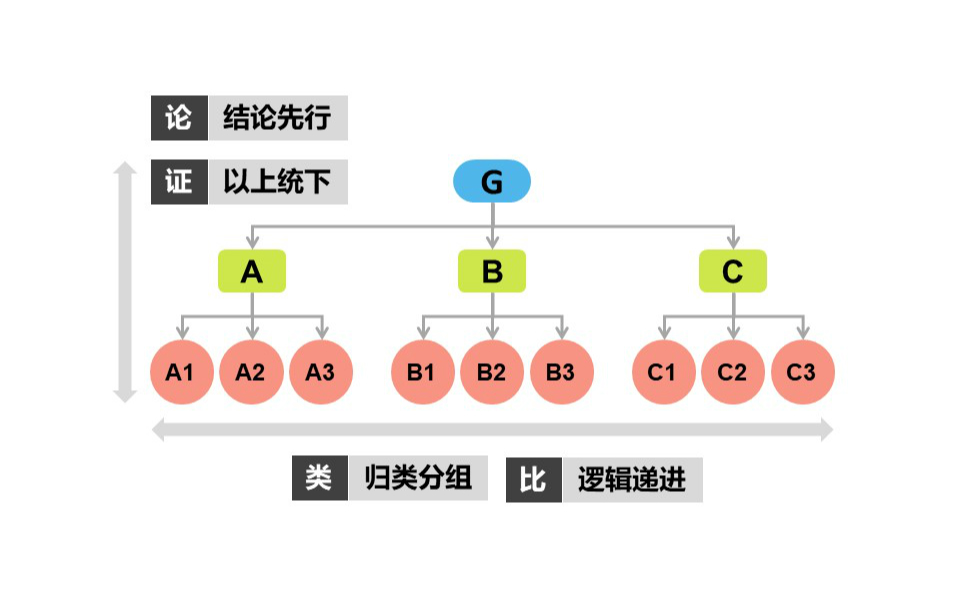
如何应用金字塔模型提高结构化表达能力
看一下结构化表达的定义: 结构化表达:是基于结构化思维,理清事物整理与部分之间关系、换位思考后,进行简洁、清晰和有信服力的表达,是一种让受众听得明白、记得清楚、产生认同的精益沟通方式。 结构化表达的基本原则是…...

2023年系统分析师考前几页纸
企业战略规划是用机会和威胁评价现在和未来的环境,用优势和劣势评价企业现状,进而选择和确定企业的总体和长远目标,制定和抉择实现目标的行动方案。信息系统战略规划关注的是如何通过该信息系统来支撑业务流程的运作,进而实现企业的关键业务目标,其重点在于对信息系统远景…...
openwrt-安装NGINX
openwrt-安装NGINX 介绍 OpenWrt 是一个用于嵌入式设备的开源操作系统。它基于 Linux 内核,并且主要被设计用于路由器和网络设备。 OpenWrt 的主要特点包括: 完全可定制:OpenWrt 提供了一个完全可写的文件系统,用户可以自定义设…...

Linux安装MongoDB数据库并内网穿透在外远程访问
文章目录 前言1.配置Mongodb源2.安装MongoDB数据库3.局域网连接测试4.安装cpolar内网穿透5.配置公网访问地址6.公网远程连接7.固定连接公网地址8.使用固定公网地址连接 转发自CSDN cpolarlisa的文章:Linux服务器安装部署MongoDB数据库 - 无公网IP远程连接「内网穿透…...

flutter系列之:使用AnimationController来控制动画效果
文章目录 简介构建一个要动画的widget让图像动起来总结 简介 之前我们提到了flutter提供了比较简单好用的AnimatedContainer和SlideTransition来进行一些简单的动画效果,但是要完全实现自定义的复杂的动画效果,还是要使用AnimationController。 今天我…...
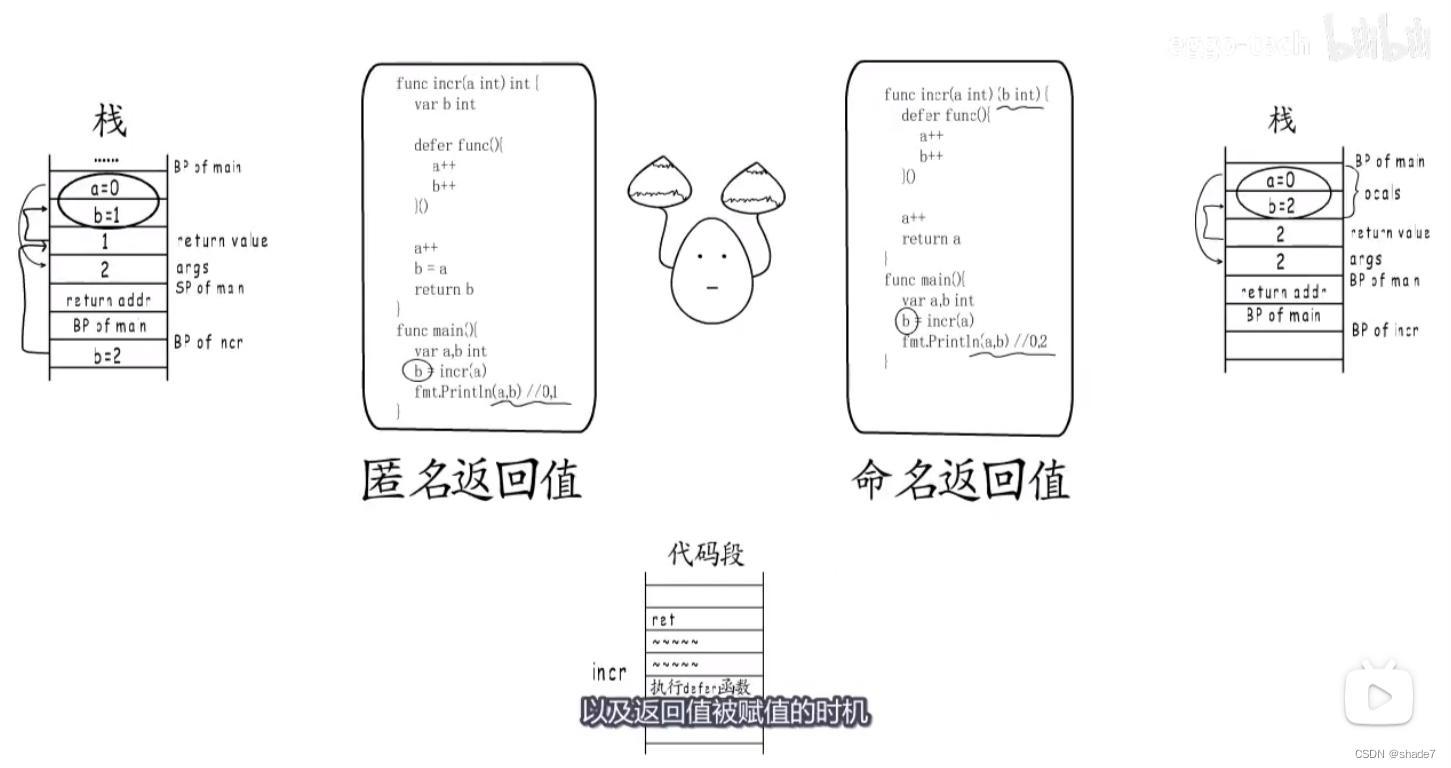
golang 函数调用栈笔记
一个被函数在栈上的情况:(栈从高地址向低地址延伸) 返回地址(函数执行结束后,会跳转到这个地址执行) BP(函数的栈基)局部变量返回值(指的是函数返回值,eg&am…...

云端一体助力体验升级和业务创新
随着音视频和AI技术的发展,在满足用户基础体验和需求情况下,更极致的用户体验和更丰富的互动玩法,成为各个平台打造核心竞争力的关键。LiveVideoStackCon 2022 北京站邀请到火山引擎视频云华南区业务负责人——张培垒,基于节跳动音…...
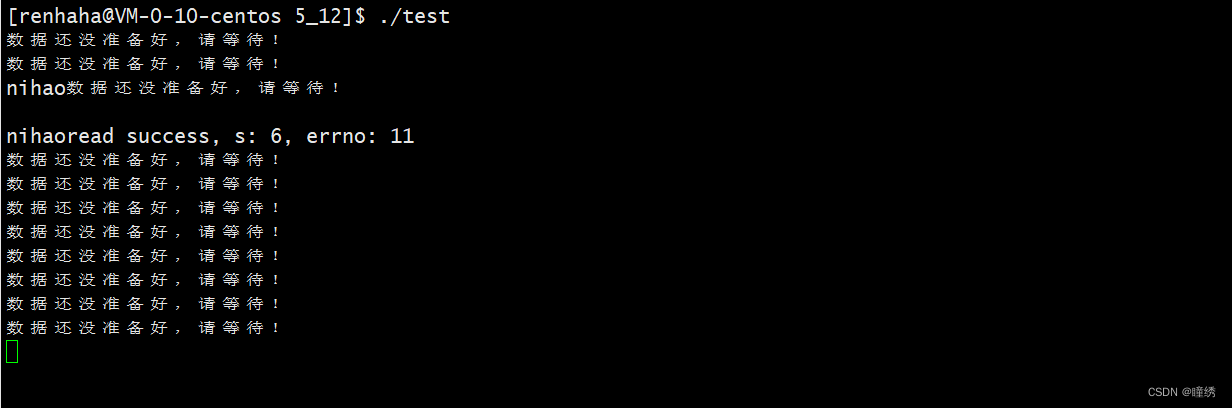
【Linux Network】高级IO
目录 前言 五种IO模型 阻塞IO 非阻塞IO 信号驱动IO IO多路转接 异步IO 小结 同步通信 vs 异步通信 阻塞 vs 非阻塞 其他高级IO 非阻塞IO fcntl函数 代码测试 高级IO🌷 前言 IO:所谓的I便是 input,所谓的O便是 output,简单点来说&a…...

Python语言基本控制结构
Python语言基本控制结构包括:条件语句:if、elif、else 循环语句:for、while 跳转语句:break、continue、return 下面是它们的基本用法: 条件语句 if condition1: statement1 elif condition2: statement2 else: stat…...

旅游网站版面设计方案
门户网站的页面设计:采用天蓝色为主色调、以红色、绿色为基调,突出网站的青春活波性。 网站风格尽量简单统一、容易让大多数上网者接受,个性化的网站,再者,网站有主体信息结构及布 word . . . . 局,它是总体…...
sudo unable to open read-only file system”的原因
此错误是由多种原因引起的,包括: 文件系统不一致。文件系统配置错误(/etc/fstab 文件中的错误条目)。由于各种原因(包括突然断电或电缆损坏)导致系统意外或突然关闭。在某些情况下,Windows 的双…...
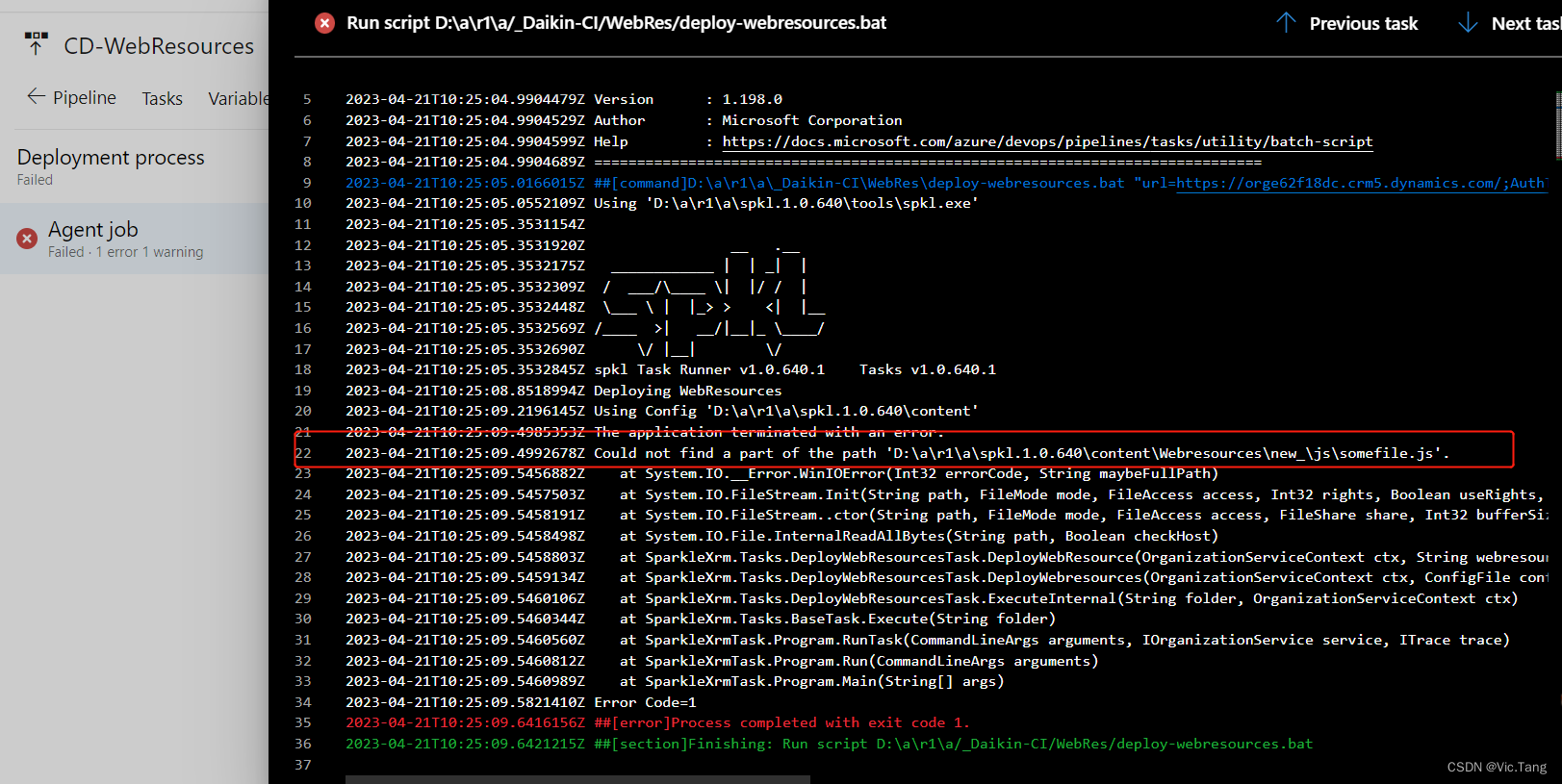
Dynamics 365 DevOps CI/CD之WebResource
对于D365自身的发布,简单点来说就是Solution的发布,复杂一些会涉及周边集成接口等一系列的发布。如果是单纯的Solution的发布的Azure DevOps商店里有很多工具,比如Power DevOps Tools,这个我之前也有博文转载过相关文章࿰…...

Linux常用指令及基础配置
Linux常用指令及基础配置 Linux系统操作指令文件管理指令系统设置相关指令addr2line的运用 vim相关vim配置操作Vim功能操作分屏擦操作删除操作换行符转换操作:文件比较合并操作折叠指令 Linux系统操作指令 文件管理指令 find ./ -iname filename find ./ -name “…...

Linux 服务器上Nvidia相关指令
1、GPU驱动的内存常驻模式 1)操作命令: 确保你具有root或sudo权限,以执行下面的命令。打开终端或命令行界面。运行以下命令来设置GPU驱动的内存常驻模式: nvidia-smi -pm 1这会将GPU驱动程序设置为内存常驻模式。 4. 验证设置是否成功。运…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...
