数据结构与算法之栈: Leetcode 682. 棒球比赛 (Typescript版)
棒球比赛
- https://leetcode.cn/problems/baseball-game/
描述
-
你现在是一场采用特殊赛制棒球比赛的记录员。这场比赛由若干回合组成,过去几回合的得分可能会影响以后几回合的得分。
-
比赛开始时,记录是空白的。你会得到一个记录操作的字符串列表 ops,其中 ops[i] 是你需要记录的第 i 项操作,ops 遵循下述规则:
- 整数 x - 表示本回合新获得分数 x
- “+” - 表示本回合新获得的得分是前两次得分的总和。题目数据保证记录此操作时前面总是存在两个有效的分数。
- “D” - 表示本回合新获得的得分是前一次得分的两倍。题目数据保证记录此操作时前面总是存在一个有效的分数。
- “C” - 表示前一次得分无效,将其从记录中移除。题目数据保证记录此操作时前面总是存在一个有效的分数。
-
请你返回记录中所有得分的总和。
示例 1
输入:ops = ["5","2","C","D","+"]
输出:30
解释:
"5" - 记录加 5 ,记录现在是 [5]
"2" - 记录加 2 ,记录现在是 [5, 2]
"C" - 使前一次得分的记录无效并将其移除,记录现在是 [5].
"D" - 记录加 2 * 5 = 10 ,记录现在是 [5, 10].
"+" - 记录加 5 + 10 = 15 ,记录现在是 [5, 10, 15].
所有得分的总和 5 + 10 + 15 = 30
示例 2:
输入:ops = ["5","-2","4","C","D","9","+","+"]
输出:27
解释:
"5" - 记录加 5 ,记录现在是 [5]
"-2" - 记录加 -2 ,记录现在是 [5, -2]
"4" - 记录加 4 ,记录现在是 [5, -2, 4]
"C" - 使前一次得分的记录无效并将其移除,记录现在是 [5, -2]
"D" - 记录加 2 * -2 = -4 ,记录现在是 [5, -2, -4]
"9" - 记录加 9 ,记录现在是 [5, -2, -4, 9]
"+" - 记录加 -4 + 9 = 5 ,记录现在是 [5, -2, -4, 9, 5]
"+" - 记录加 9 + 5 = 14 ,记录现在是 [5, -2, -4, 9, 5, 14]
所有得分的总和 5 + -2 + -4 + 9 + 5 + 14 = 27
示例 3:
输入:ops = ["1"]
输出:1
提示
- 1 <= ops.length <= 1000
- ops[i] 为 “C”、“D”、“+”,或者一个表示整数的字符串。整数范围是 [-3 * 1 0 4 10^4 104, 3 * 1 0 4 10^4 104]
- 对于 “+” 操作,题目数据保证记录此操作时前面总是存在两个有效的分数
- 对于 “C” 和 “D” 操作,题目数据保证记录此操作时前面总是存在一个有效的分数
算法实现
1 )方案 1
function calPoints(operations: string[]): number {// 用于存放历史数据的数组let result:number[] = []// 上一轮的数据let pre1: number// 上上轮的数据let pre2: number// 对数组进行遍历,遍历的目的是处理得分operations.forEach((item: any) => {switch (item) {case 'C':if (result.length) {result.pop()}breakcase 'D':pre1 = result.pop()result.push(pre1, pre1 * 2)breakcase '+':pre1 = result.pop()pre2 = result.pop()result.push(pre2, pre1, pre2 + pre1)breakdefault:result.push(item * 1)}})// 返回一个累加器return result.reduce((total, num) => { return total + num }, 0)
};
- 就是按照题目要求,一步一步操作,进栈出栈
- 这个代码比较长,有些面向过程编程的感觉
2 )方案 2
function calPoints(operations: string[]): number {// 初始化容器const numStack: number[] = [];// 累加器const sum = (nums: number[]) => {return nums.reduce((i, j) => i + j, 0);}// 操作对应数组const operationMap = {C: () => numStack.pop(),D: () => numStack.push(numStack[numStack.length - 1] * 2),'+': () => numStack.push(sum(numStack.slice(-2))),}// 遍历操作数进行匹配操作operations.forEach(o => {Number(o) ? numStack.push(Number(o)) : operationMap[o]()})return sum(numStack);
};
- 这是官方示例,这里数据结构设置的比较合适
- 使用Map结构存储操作函数,对数据进行处理
- 方案2比方案1要精简,代码质量更高
相关文章:
)
数据结构与算法之栈: Leetcode 682. 棒球比赛 (Typescript版)
棒球比赛 https://leetcode.cn/problems/baseball-game/ 描述 你现在是一场采用特殊赛制棒球比赛的记录员。这场比赛由若干回合组成,过去几回合的得分可能会影响以后几回合的得分。 比赛开始时,记录是空白的。你会得到一个记录操作的字符串列表 ops&a…...

E-office Server_v9.0 漏洞分析
漏洞简介 泛微e-office是一款标准化的协同OA办公软件,实行通用化产品设计,充分贴合企业管理需求,本着简洁易用、高效智能的原则,为企业快速打造移动化、无纸化、数字化的办公平台。由于泛微 E-Office 未能正确处理上传模块中输入…...

MySQL数据库,JDBC连接数据库操作流程详细介绍
前言: 在学完 MySQL 和 Java 后,我们通常会尝试使用 Java编译器 连接 MySQL数据库,从而达到使用编译器来操作数据库的效果。连接的这个过程会用 JDBC 相关知识,因此我把 JDBC 包的下载及导入流程,以及 JDBC 的使用流程…...
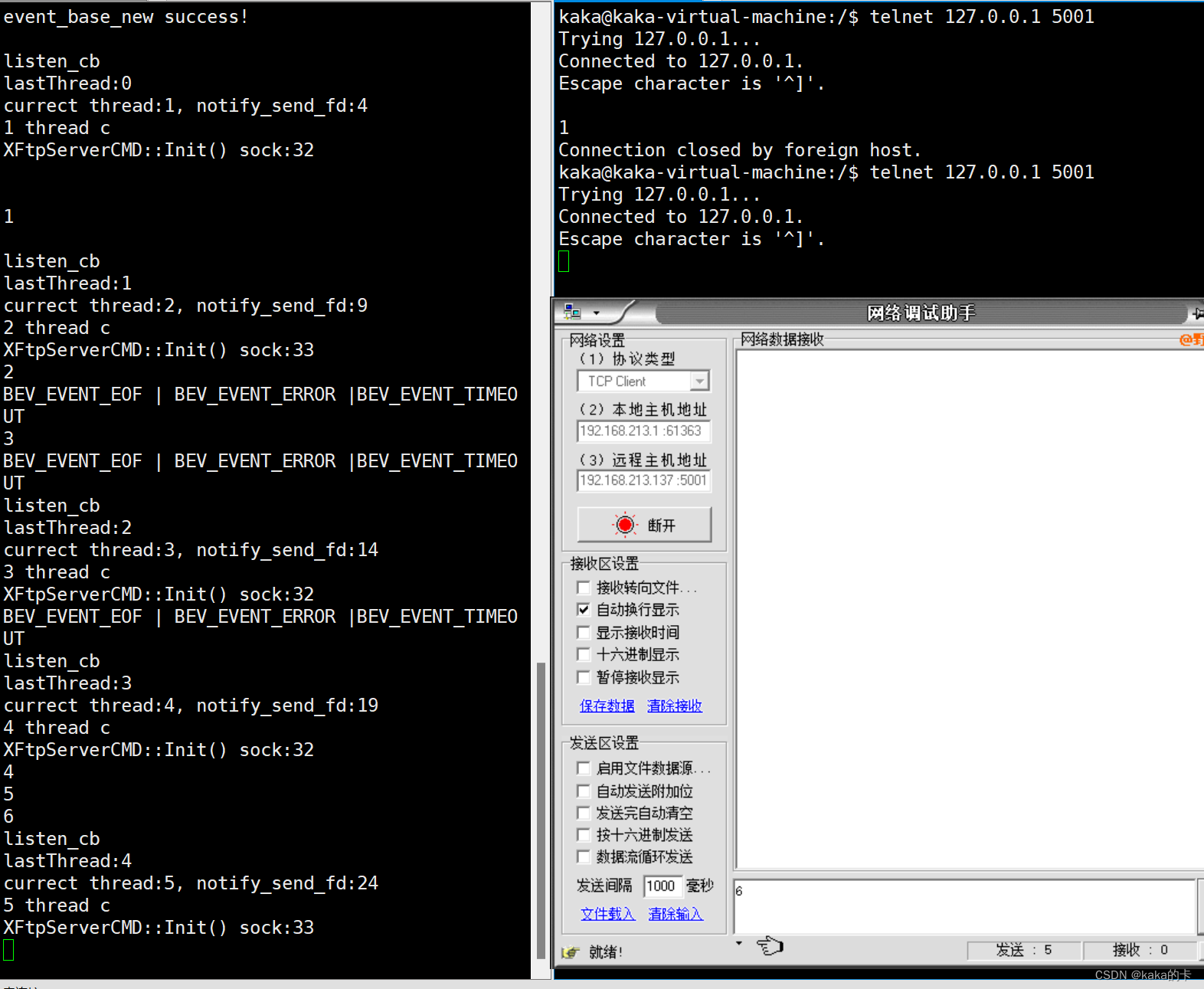
libevent高并发网络编程 - 06_基于libevent的C++线程池实现
文章目录 1 功能简介线程池的初始化线程池执行流程 2 线程池类的设计线程类XThreadXThread.hXThread.cpp 线程池类XThreadPoolXThreadPool.hXThreadPool.cpp 任务基类taskXTask.h 3 自定义任务的例子自定义任务类ServerCMDServerCMD.hServerCMD.cpp 测试程序运行效果 1 功能简介…...

【Java EE 初阶】线程安全及死锁解决方案
目录 1.多线程下线程不安全的问题 1.使用多个线程对Array List集合进行添加操作并打印,查看结果 2.如何在多线程环境下使用线程安全的集合类 CopyOnWriteArrayList 3.多线程环境下使用队列 4.多线程环境下使用哈希表 1.HashTable线程安全 2.Concurrent Hash M…...
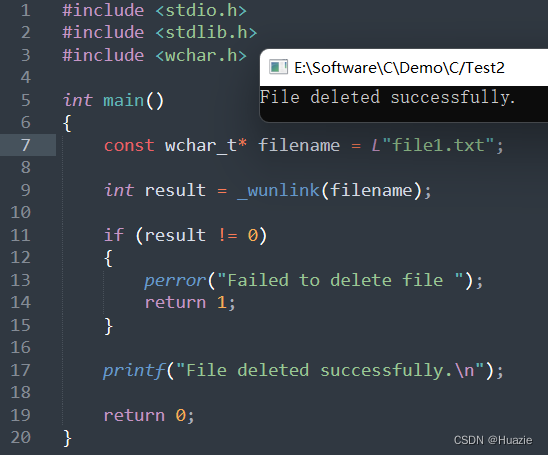
C语言函数大全-- _w 开头的函数(5)
C语言函数大全 本篇介绍C语言函数大全-- _w 开头的函数 1. _wspawnl 1.1 函数说明 函数声明函数功能int _wspawnl(int mode, const wchar_t* cmdname, const wchar_t* arglist, ...);启动一个新的进程并运行指定的可执行文件 参数: mode : 启动命令的…...

机械大专生能学会云计算吗,完全零基础的
机械大专生能学会云计算吗,完全零基础的 正常来说,大专及以上学历都能学会云计算,但是会和满足就业需求是两回事哈。如果你想通过学习就业,就需要根据当下相关岗位的普遍技术需求以及其他方面的要求,来针对性的学习和提…...
腾讯云EdgeOne为什么能让客户降本增效?
随着数字化时代的来临,各类线上互动场景不断出现,并成为人们日常工作生活中的一部分。然而,基于互联网提供线上娱乐、线上办公、线上购物等服务的企业,在复杂的全球网络环境下会遇到网络延迟不稳定的情况,海外环境更多…...

基于粒子群算法的微网经济优化调度——附Matalb代码
目录 摘要: 代码主要内容: 研究背景: 微电网模型: 粒子群算法: 运行结果: Matlab代码分享: 摘要: 提出了一种经济与环保相协调的微电网优化调度模型,针对光伏电池…...
Flink入门
目录 一、Flink简介 二、为什么选择Flink 三、与传统数据处理架构相比 四、Flinik批处理数据基础代码 五、Flink流处理基础代码 一、Flink简介 Apache Flink 是一个框架和分布式处理引擎,用于对无界和有界数 据流进行状态计算。 二、为什么选择Flink 流数据更…...

【Go微服务开发】gin+grpc+etcd 重构 grpc-todolist 项目
写在前面 最近稍微重构了之前写的 grpc-todolist 模块 项目地址:https://github.com/CocaineCong/grpc-todoList 1. 项目结构改变 与之前的目录有很大的区别 1.1 grpc_todolist 项目总体 1.1.1 改变前 grpc-todolist/ ├── api-gatway // 网关模块 ├── ta…...
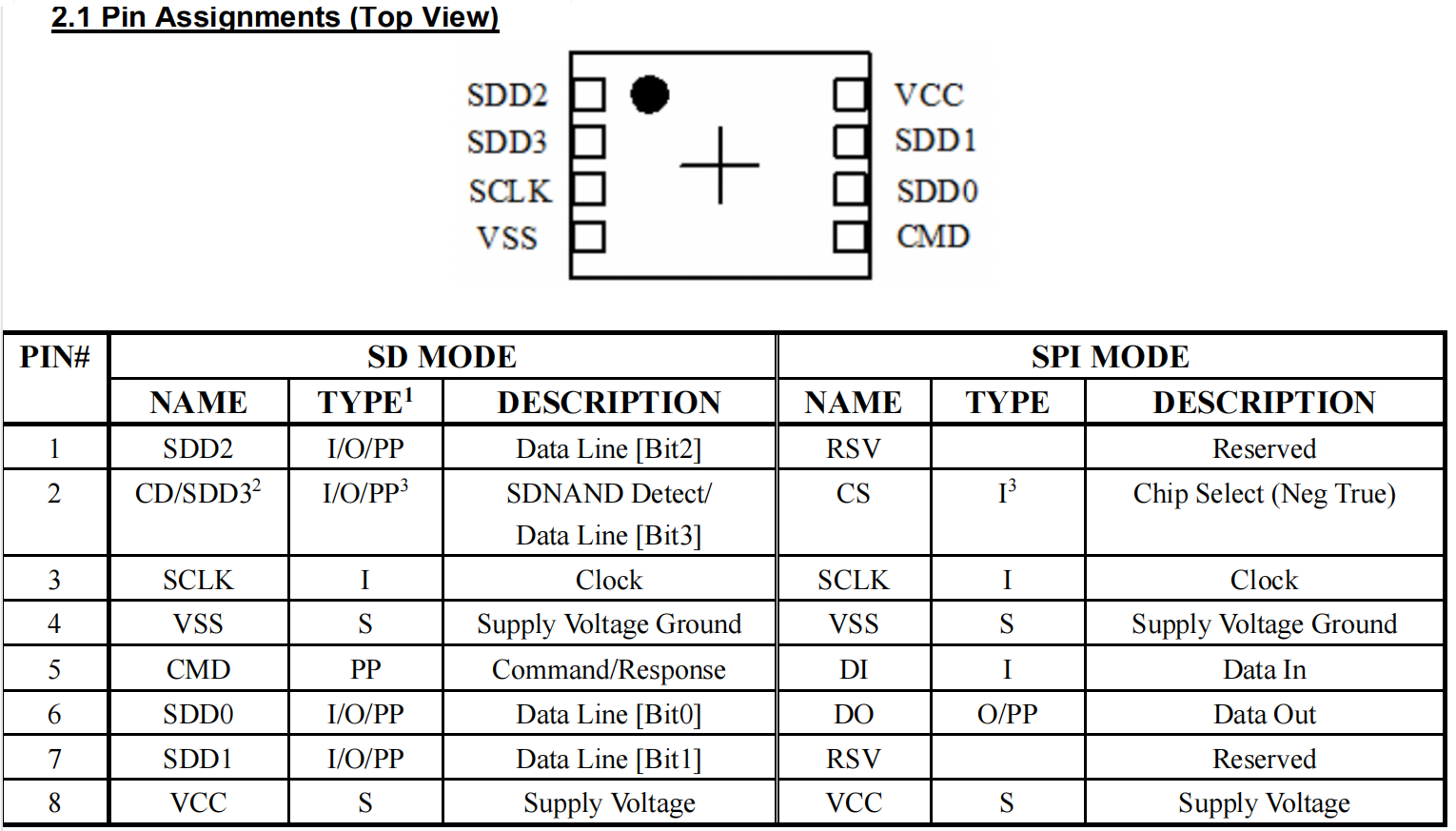
单板硬件设计:存储器SD卡( NAND FLASH)
在单板设计中,无论是涉及到一个简易的CPU、MCU小系统或者是复杂的单板设计,都离不开存储器设计: 1、存储器介绍 存储器的分类大致可以划分如下: ROM和RAM指的都是半导体存储器,ROM在系统停止供电的时候仍然可以保持数…...

C++实现日期类Date(超详细)
个人主页:平行线也会相交💪 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创 收录于专栏【C之路】💌 本专栏旨在记录C的学习路线,望对大家有所帮助🙇 希望我们一起努力、成长&…...
实验室检验系统源码,集检验业务、质量控制、报告、统计分析、两癌等模块于一体
云 LIS 系统针对区域化 LIS 而设计,依托底层云架构,将传统的 LIS 功能模块进行“云化”。 该系统是集检验业务、科室管理、质量控制、报告、统计分析、两癌等模块于一体的数据检验信息平台。通过计算机联网,实现各类仪器数据结果的实时自动接…...
学习RHCSA的day.03
目录 2.6 Linux系统的目录结构 2.7 目录操作命令 2.8 文件操作命令 2.6 Linux系统的目录结构 1、Linux目录结构的特点 分区加载于目录结构: 使用树形目录结构来组织和管理文件。整个系统只有一个位于根分区的一个根目录(树根)、一棵树。…...
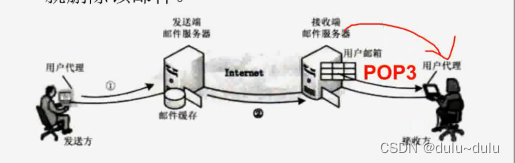
电子邮件协议(SMTP,MIME,POP3,IMAP)
SMTP 关键词: 电子邮件协议:SMTP简单邮件传输协议,负责将邮件上传到服务器,采用TCP的25端口,C/S工作。仅传送ASCII码文本 详细介绍: SMTP是一种提供可靠且有效的电子邮件传输的协议。SMTP是建立在FTP文件传输服务上…...

Golang笔记:使用embed包将静态资源嵌入到程序中
文章目录 目的使用演示//go:embed 指令在WebServer中应用总结 目的 Golang编译程序默认是静态编译,会把相关的库都打包到一起,这在分发部署使用时非常方便。不过如果项目中用到的外部的静态资源文件,通常就需要将这些资源和程序一起拷贝分发…...

ImportError: cannot import name ‘OldCsv‘ from ‘pyflink.table.descriptors‘
我最近开始使用flink用于数据处理。 当我尝试执行table api 用于计数时 我不能导入OldCsv and FileSystem from pyflink.table.descriptors. I have also downloaded apache-flink using: pip install apache-flink [rootmaster flink]# pip3 list | grep flink apache-fli…...

YouCompleteMe(YCM)安装
vim在各个linux版本中是个比较好编辑器,反正nano我是用不惯。但这个ycm的安装也是不断的在变,现在的安装比之前要简单的多,基本个几命令就搞定了,而且 也不用关心系统里有没有vim,ycm已经可以自动安装。具体安装步骤如下ÿ…...
day33_css
今日内容 零、 复习昨日 一、CSS 零、 复习昨日 见代码 一 、引言 1.1CSS概念 层叠样式表(英文全称:Cascading Style Sheets)是一种用来表现HTML(标准通用标记语言的一个应用)或XML(标准通用标记语言的一个子集)等文…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...
