图论专题(一)
图论专题(一)
参考文献
- BFS和DFS的直观解释 https://blog.csdn.net/c406495762/article/details/117307841
- Leetcode岛屿问题系列分析 https://blog.csdn.net/qq_39144436/article/details/124173504
- 多源广度优先 https://blog.csdn.net/peko1/article/details/121989497
- 拓扑排序 https://blog.csdn.net/chenweiye1/article/details/113563417
- Trie树 https://blog.csdn.net/weixin_47251999/article/details/113364363
- 字典树 https://baike.baidu.com/item/%E5%AD%97%E5%85%B8%E6%A0%91/9825209?fromtitle=Trie%E6%A0%91&fromid=517527&fr=aladdin
常见问题
1. BFS & DFS
- 广度优先搜索算法(Breadth-First-Search,缩写为 BFS),是一种利用队列实现的搜索算法。简单来说,其搜索过程和 “湖面丢进一块石头激起层层涟漪” 类似。
- BFS常用于找单一的最短路。约束:每条路上的权重必须是1
- 一般来说BFS可以用以下模板思路来解决
(1) 初始化队列
(2) 起始点入队
(3) 循环:队列不为空时,先弹出队首元素,然后将这个元素能够处理的其他点全部入队
- 深度优先搜索算法(Depth-First-Search,缩写为 DFS),是一种利用递归实现的搜索算法。简单来说,其搜索过程和 “不撞南墙不回头” 类似。
- DFS 用于找所有解的问题,它的空间效率高,但是找到的不一定是最优解,必须记录并完成整个搜索,故一般情况下,深搜需要非常高效的剪枝
- BFS 的重点在于队列,而 DFS 的重点在于递归。这是它们的本质区别。
2. 拓扑排序
- 定义
1.有向无环图
2.序列里的每一个点只能出现一次
3.任何一对 u 和 v ,u 总在 v 之前(这里的两个字母分别表示的是一条线段的两个端点,u 表示起点,v 表示终点)
- 求拓扑排序的思路:
(1) 计算所有节点的入度
(2) 入度=0的节点入队
(3) 循环:队列不为空时,弹出队首元素,用队首节点a更新其他所有节点的入度(与其相邻的节点b/c/```入度-1,注意边的方向一定是a到其他节点),更新完入度=0的节点入队
3. Trie(前缀树)
- 定义
又称单词查找树,Trie树,是一种树形结构,是一种哈希树的变种。
典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。
优点:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。
- 分析(以下均来源参考文献5)
- 时间复杂度
- 构建Trie树时间复杂度是 O(n)(n是Trie树中所有元素的个数)
- 查询Trie树时间复杂度是 O(k)(k 表示要查找的字符串的长度)
- 缺陷
- 每个数组元素要存储一个 8 字节指针(或者是 4 字节,这个大小跟 CPU、操作系统、编译器等有关),且指针对CPU缓存并不友好。
- 在重复的前缀并不多的情况下,Trie 树不但不能节省内存,还有可能会浪费更多的内存。(比如,此种字符串第三个字符只有两种可能,而它要维护一个长26的数组。这还只是考虑纯字母的情况,如果是复合型字符串,则会浪费更多空间)
- 应用
- 第一,字符串中包含的字符集不能太大。如果字符集太大,那存储空间可能就会浪费很多。即便可以优化,但也要付出牺牲查询、插入效率的代价。
- 第二,要求字符串的前缀重合比较多,不然空间消耗会变大很多。
- 第三,通过指针串起来的数据块是不连续的。所以,对缓存并不友好,性能上会打个折扣。
- 第四,对于精确查找(如词频统计),用字符串hash/红黑树其实更好,Trie树比较适合的是查找前缀匹配的字符串(如 实现搜索引擎的搜索关键词提示功能)
- 时间复杂度
例题
1. BFS & DFS
- BFS和DFS在做题的时候一般可以相互转换,可以根据题干自行选择较优的那一种(比如最短路一般用广度优先)
岛屿问题(做之前建议先阅读一下参考文献2, 大佬讲的很好)
- 先记录一下DFS的模板(模板内容均来源参考文献2)
- 二叉树
- 二叉树的 DFS 有两个要素:「访问相邻结点」和「判断 base case」。
- 第一个要素是访问相邻结点。二叉树的相邻结点非常简单,只有左子结点和右子结点两个。二叉树本身就是一个递归定义的结构:一棵二叉树,它的左子树和右子树也是一棵二叉树。那么我们的 DFS 遍历只需要递归调用左子树和右子树即可。
- 第二个要素是 判断 base case。一般来说,二叉树遍历的 base case 是 root == null。这样一个条件判断其实有两个含义:一方面,这表示 root 指向的子树为空,不需要再往下遍历了。另一方面,在 root == null 的时候及时返回,可以让后面的 root.left 和 root.right 操作不会出现空指针异常。
void traverse(TreeNode* root) {// 判断 base caseif (root == NULL) {return;}// 访问两个相邻结点:左子结点、右子结点traverse(root->left);traverse(root->right);
}
- 图
- 对于网格上的 DFS,我们完全可以参考二叉树的 DFS,写出网格 DFS 的两个要素:
- 首先,网格结构中的格子有多少相邻结点?答案是上下左右四个。对于格子 (r, c) 来说(r 和 c 分别代表行坐标和列坐标),四个相邻的格子分别是 (r-1, c)、(r+1, c)、(r, c-1)、(r, c+1)。换句话说,网格结构是「四叉」的。
- 其次,网格 DFS 中的 base case 是什么?从二叉树的 base case 对应过来,应该是网格中不需要继续遍历、grid[r][c] 会出现数组下标越界异常的格子,也就是那些超出网格范围的格子。
- 网格结构的 DFS 与二叉树的 DFS 最大的不同之处在于,遍历中可能遇到遍历过的结点。这是因为,网格结构本质上是一个「图」,我们可以把每个格子看成图中的结点,每个结点有向上下左右的四条边。在图中遍历时,自然可能遇到重复遍历结点。这时候,DFS 可能会不停地「兜圈子」,永远停不下来。–> 需要标记已经遍历过的格子
void dfs(int[][] grid, int r, int c) {// 判断 base case// 如果坐标 (r, c) 超出了网格范围,直接返回if (!inArea(grid, r, c)) {return;}// 访问上、下、左、右四个相邻结点dfs(grid, r - 1, c);dfs(grid, r + 1, c);dfs(grid, r, c - 1);dfs(grid, r, c + 1);
}// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {return 0 <= r && r < grid.length && 0 <= c && c < grid[0].length;
}
- 岛屿数量 https://leetcode.cn/problems/number-of-islands/?envType=study-plan-v2&id=top-100-liked
这题实际上就是求由’1’构成的连通图的个数。即:在给定的图中,有多少块’1’。比如以下测试用例包含3个由’1’构成的连通图。
[“1”,“1”,“0”,“0”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“1”,“0”,“0”],
[“0”,“0”,“0”,“1”,“1”]
因此思路如下:对于每个连通块,从它的入口处(即遍历grid时, 遇到的第一个这个连通图中的节点)开始bfs/dfs, 遍历连通块时把其中的每个节点都做上标记(表明已经遍历过了), 后续遇到这个连通块中的节点时就不会再以其为入口做bfs/dfs。这样,从头把grid网格遍历一遍,就能得到所有的连通块。代码实现很简单,把板子敲出来就行。
- 深度优先
class Solution {
public:bool flag[90010];void dfs(int x,int y,vector<vector<char>>& grid){int m=grid.size();int n=grid[0].size();cout<<x<<" "<<y<<endl;if(x<0||x>=m||y<0||y>=n||grid[x][y]=='0'||flag[x*n+y]) return;if(grid[x][y]=='1'&&!flag[x*n+y]) flag[x*n+y]=true;dfs(x+1,y,grid);dfs(x-1,y,grid);dfs(x,y+1,grid);dfs(x,y-1,grid);}int numIslands(vector<vector<char>>& grid) {int res=0;int m=grid.size();int n=grid[0].size();for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(grid[i][j]=='1'&&!flag[i*n+j]){res++;dfs(i,j,grid);}}}return res;}
};
- 广度优先
class Solution {
public:bool flag[90010];void bfs(int x,int y,vector<vector<char>>& grid){int m=grid.size();int n=grid[0].size();queue<int> q; //存坐标q.push(x*n+y);flag[x*n+y]=true;int dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};while(!q.empty()){int t=q.front();q.pop();for(int i=0;i<4;i++){int x=t/n+dx[i];int y=t%n+dy[i];if(x>=0 && x<m && y>=0 && y<n && grid[x][y]=='1' && !flag[x*n+y]){ //陆地,且还没被遍历过q.push(x*n+y);flag[x*n+y]=true;} }}}int numIslands(vector<vector<char>>& grid) {int res=0;int m=grid.size();int n=grid[0].size();for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(grid[i][j]=='1'&&!flag[i*n+j]){res++;bfs(i,j,grid);}}}return res;}
};
- 岛屿的最大面积 https://leetcode.cn/problems/max-area-of-island/
思路和上题基本上是一样的,只要在每次遍历时记录当前连通块的面积,并且以此不断更新最大面积就行。
- 深度优先
class Solution {
public:bool flag[2510];void dfs(int x,int y,vector<vector<int>>& grid,int& square){int m=grid.size();int n=grid[0].size();if(x<0||x>=m||y<0||y>=n||grid[x][y]==0||flag[x*n+y]){ //xy越界 or 遍历到的是0 or 遍历到的是已处理过的1 return;} square++;flag[x*n+y]=true;dfs(x+1,y,grid,square);dfs(x-1,y,grid,square);dfs(x,y+1,grid,square);dfs(x,y-1,grid,square);}int maxAreaOfIsland(vector<vector<int>>& grid) {int m=grid.size();int n=grid[0].size();int maxSquare=0;for(int i=0;i<m;i++){for(int j=0;j<n;j++){int square=0;if(grid[i][j]==1&&!flag[i*n+j]){dfs(i,j,grid,square);maxSquare=max(maxSquare,square);}}}return maxSquare;}
};
- 广度优先
class Solution {
public:bool flag[2510];int bfs(int x,int y,vector<vector<int>>& grid){int m=grid.size();int n=grid[0].size();int square=0;queue<int> q;q.push(x*n+y);flag[x*n+y]=true;int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};while(!q.empty()){square++;int t=q.front();q.pop();for(int i=0;i<4;i++){int x=t/n+dx[i];int y=t%n+dy[i];if(x>=0 && x<m && y>=0 && y<n && grid[x][y]==1 && !flag[x*n+y]){q.push(x*n+y);flag[x*n+y]=true;}}}return square;}int maxAreaOfIsland(vector<vector<int>>& grid) {int m=grid.size();int n=grid[0].size();int maxSquare=0;for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(grid[i][j]==1&&!flag[i*n+j]) maxSquare=max(maxSquare,bfs(i,j,grid)); }}return maxSquare;}
};
- 岛屿的周长
这题的思路稍微有一点不一样。(=.= 不是很懂为什么三题难度差不多,这题是easy前两题是medium)题目给的数据保证了图中只有一个连通块,而我们要做的是在遍历到连通块中的每一个节点时,记录下这个节点对整个连通块周长产生的影响。具体思路是分别check这个节点前后左右的情况,以此来确定其对周长的贡献。分三种情况:
(1) 当前节点前/后/左/右方向上是海洋 --> 说明这个节点在这个方向上,是连通块的边缘,因此对连通块周长的贡献是+1
(2) 当前节点没有前/后/左/右节点 --> 和(1)本质上是一样的。说明这个节点在这个方向上,是连通块的边缘,因此在这个方向(前/后/左/右)上其对连通块周长的贡献是+1
(3) 当前节点前/后/左/右方向上是陆地,且已经被check过 --> 说明节点在这个方向上的边已经在连通块内部, 不会对连通块的周长产生任何影响, +0
(4) 当前节点前/后/左/右方向上是陆地(1),且没有被check过 --> 搜索这个新找到的1节点
需要注意的是,之前做BFS/DFS的题基本都是check某个节点的周边四个节点,而这题严格意义上来说是check某个节点的四条边,也算提醒了一下自己不要固定思维
- 深度优先
class Solution {
public:bool flag[10010];int dfs(int x,int y,vector<vector<int>>& grid){int m=grid.size();int n=grid[0].size();if(x<0||x>=m||y<0||y>=n) return 1;if(grid[x][y]==0) return 1;if(flag[x*n+y]) return 0;flag[x*n+y]=true;return dfs(x-1,y,grid)+dfs(x+1,y,grid)+dfs(x,y-1,grid)+dfs(x,y+1,grid);}int islandPerimeter(vector<vector<int>>& grid) {int m=grid.size();int n=grid[0].size();int sum=0;for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(grid[i][j]==1&&!flag[i*n+j]){sum=dfs(i,j,grid);break;}}}return sum; }
};
- 广度优先
class Solution {
public:bool flag[10010];void bfs(int x,int y,vector<vector<int>>& grid,int& sum){int m=grid.size();int n=grid[0].size();queue<int> q;q.push(x*n+y);flag[x*n+y]=true;int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};while(!q.empty()){int t=q.front();q.pop();for(int i=0;i<4;i++){ //对每一个节点,搜寻其前后左右的点,以计算这个点给整个岛屿增加的周长int x=t/n+dx[i];int y=t%n+dy[i];if(x<0||x>=m||y<0||y>=n) sum+=1; //x的前后左右某个点越界了-->说明x的前后左右有一条是边界边,长度为1else if(grid[x][y]==0) sum+=1; //x的前后左右某个点是海洋-->x的前后左右有一条是邻接海洋的边,长度为1else if(flag[x*n+y]) sum+=0; //x的前后左右有某个点是陆地,而且已经被check过了-->x的这条边在岛屿内部,不会对整个岛屿的周长造成变化else{ //x的前后左右有某个点是陆地,且还没有被check过-->这个点可以被组成岛屿的一部分,把它入队,后续对它计算能够给岛屿增加的周长q.push(x*n+y);flag[x*n+y]=true;} }}}int islandPerimeter(vector<vector<int>>& grid) {int m=grid.size();int n=grid[0].size();int sum=0;for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(grid[i][j]==1&&!flag[i*n+j]){bfs(i,j,grid,sum);break;}}}return sum; }
};
- 腐烂的橘子
这题首先有四个注意点:
(1) 这题显然是一个最短路问题(寻找每一个新鲜橘子的最小腐烂时间),所以建议用广度优先。深度优先不能保证第一次搜到的就是最短路。
(2) 这题是一个多源广度优先问题,和单源的相比,多源广度优先只需要在初始化队列时把所有源都入队就行了(单源只需要入队一个源)。
(3) 对于这题的BFS,没必要单开一个数组来记录每个橘子的状态情况,直接在源grid数组上修改就行了(bfs后,grid中:空单元格为0,新鲜橘子格为1,腐烂橘子格为腐烂时间+2;+2是因为原grid数组用2来表示腐烂的橘子,导致这么做的话腐烂起始时间为2,事实上把这个2换成其他所有数字都可以,只需要注意在最后还原出真实时间的时候把这个数减掉就好了)
(4) 这题其实还带了点动态规划的思想:对于每一个从新鲜变腐烂的橘子,它的腐烂时间一定是把腐烂传播给它的橘子的腐烂时间+1。
明确以上注意点后,我们可以总结出思路(参考文献3中给的,这里直接搬过来了,感谢大佬分享):
初始我们将腐烂的橘子都入队列,并记录新鲜的橘子的个数,如果最后还剩余新鲜的橘子我们就返回-1。如何处理这一时刻遍历的腐烂的橘子的最小时间呢,因为我们是让所有最初腐烂的橘子同一时刻开始传递腐烂,因此我们可以借助动态规划的思想:此时刻遍历的橘子的被腐烂的时间,一定等于让他腐烂的橘子的腐烂时间+1。,因此我们可以在原数组上直接修改,假设此时是grid[x][y]遍历到grid[dx][dy],那么我们可以得出:grid[dx][dy]=grid[x][y]+1;最后我们考虑最初的橘子的值是2,但是他的腐烂时间是0,因此此时刻此橘子的腐烂时间ans=grid[dx][dy]-2
- 广度优先
class Solution {
public:int orangesRotting(vector<vector<int>>& grid) {int m=grid.size();int n=grid[0].size();queue<int> q; //存放所有腐烂的橘子 int cnt=0; //新鲜橘子数(用于最后判断要不要返回-1)for(int i=0;i<m;i++){ //多源DFS(首先把所有源入队,后续和单源差不多)for(int j=0;j<n;j++){if(grid[i][j]==2) q.push(i*n+j);else if(grid[i][j]==1) cnt++;}}int dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};int time=0;//事实上bfs后,grid中:空单元格为0,新鲜橘子格为1,腐烂橘子格为腐烂时间+2while(!q.empty()){auto t=q.front();q.pop();for(int i=0;i<4;i++){int x=t/n+dx[i];int y=t%n+dy[i];if(x>=0 && x<m && y>=0 && y<n && grid[x][y]==1){ //如果是新鲜橘子,cnt--, 记录其腐烂时间(修改grid中对应值)并入队cnt--;grid[x][y]=grid[t/n][t%n]+1;q.push(x*n+y);time=grid[x][y]-2; //不断更新最新时间, -2是因为时间一开始是从2开始计算的(因为用2代表腐烂的橘子),同时用grid来记录时间也避免了用flag数组来判断某个节点是否遍历过,优化了空间}}}if(!cnt) return time; //没有新鲜橘子return -1;}
};
- 01 矩阵 https://leetcode.cn/problems/01-matrix/
本题也是多源bfs,和上一题思路差不多。本题需要单独开一个seen数组来判断每个网格是否已经被处理过。(之所以在第一次访问时就要把网格的状态记录为已处理,后续所有访问到该网格的情况不再被考虑, 是因为本题求的其实是最短路问题,而bfs求的最短路一定是第一次访问到该点时的路径长度)
class Solution {
public:vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {int m=mat.size();int n=mat[0].size();queue<pair<int,int>> q;vector<vector<int>> seen(m,vector<int> (n,0)); //0代表当前网格没被搜索过for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(!mat[i][j]){q.push({i,j});seen[i][j]=1;} }}vector<vector<int>> res(m,vector<int> (n,0));int dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};while(q.size()){auto t=q.front();q.pop();for(int i=0;i<4;i++){int x=t.first+dx[i];int y=t.second+dy[i];if( x>=0 && x<m && y>=0 && y<n && !seen[x][y] ){ //这里不用判断mat[x][y]是否为0, 因为所有为0的mat[x][y]的对应flag值已经被初始化为1res[x][y]=res[t.first][t.second]+1;seen[x][y]=1;q.push({x,y});}}}return res;}
};
2. 拓扑排序
- 有向图的拓扑序列 https://www.acwing.com/problem/content/850/
先上板子,背就是了
#include<iostream>
#include<cstring>
using namespace std;const int N=1e5+10;
int n,m;
int h[N],e[2*N],ne[2*N],idx; //邻接表存储图
int d[N]; //图中每个节点的入度
int queue[N],hh,tt; //用于bfs的队列void init(){hh=0,tt=-1;memset(h,-1,sizeof(h));
}void add(int a,int b){e[idx]=b;ne[idx]=h[a];h[a]=idx++;d[b]++;
}void bfs(){for(int i=1;i<=n;i++){ //初始化队列(先把所有入度为0的点入队)if(!d[i]) queue[++tt]=i;}while(hh<=tt){ //队列非空时int x=queue[hh++];for(int i=h[x];i!=-1;i=ne[i]){int b=e[i];d[b]--;if(!d[b]) queue[++tt]=b;}}//存在拓扑序列的话, 此时整个队列里存的就是拓扑序列了, 遍历后输出if(tt==n-1){ //图中的所有点都入队, 说明存在拓扑序列for(int i=0;i<n;i++) cout<<queue[i]<<" ";cout<<endl;}else{cout<<-1<<endl;}
}int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n>>m;init();while(m--){int x,y;cin>>x>>y;add(x,y); //有向图只需要add(x,y)}bfs();return 0;
}
- 课程表 II https://leetcode.cn/problems/course-schedule-ii/
其实也是板子题,难在建图。题目中给的数组prerequisites实际上就描述了图中节点之间边的关系,如prerequisites有元素[lessonA, lessonB],说明要上A课之前必须先把B上了。翻译一下就是B在拓扑序列中一定得在A的前面,再翻译一下就是图中有一条B–>A的有向边。根据这个思路把图建出来,再把板子默出来就完事了。
class Solution {
public:int h[2010],e[4020],ne[4020],idx; //e和ne要多开一倍,防止所有课程之间都有两条边(如a和b之间有a-->b和b-->a)int d[2010];int q[2010],hh,tt;void init(){hh=0,tt=-1;memset(h,-1,sizeof(h));}void add(int a,int b){ //边a-->be[idx]=b;ne[idx]=h[a];h[a]=idx++;d[b]++;}vector<int> bfs(int n){for(int i=0;i<n;i++){if(!d[i]) q[++tt]=i;}while(hh<=tt){int x=q[hh++];for(int i=h[x];i!=-1;i=ne[i]){int j=e[i];d[j]--;if(!d[j]) q[++tt]=j;}}vector<int> res;if(tt==n-1){for(int i=0;i<n;i++) res.push_back(q[i]);}return res;}vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {init();for(int i=0;i<prerequisites.size();i++){int a=prerequisites[i][1];int b=prerequisites[i][0];add(a,b);}return bfs(numCourses);}
};
- 课程表 https://leetcode.cn/problems/course-schedule/
这题和上一题几乎一模一样,代码都不怎么需要改。唯一的区别就是上一题需要返回拓扑序列/空数组,这一题判断一下返回值是不是空数组,是的话说明不存在拓扑序列,也就是不能完成所有课程,返回false;不是的话则返回true。
class Solution {
public:int h[2010],e[4020],ne[4020],idx; //e和ne要多开一倍,防止所有课程之间都有两条边(如a和b之间有a-->b和b-->a)int d[2010];int q[2010],hh,tt;void init(){hh=0,tt=-1;memset(h,-1,sizeof(h));}void add(int a,int b){ //边a-->be[idx]=b;ne[idx]=h[a];h[a]=idx++;d[b]++;}vector<int> bfs(int n){for(int i=0;i<n;i++){if(!d[i]) q[++tt]=i;}while(hh<=tt){int x=q[hh++];for(int i=h[x];i!=-1;i=ne[i]){int j=e[i];d[j]--;if(!d[j]) q[++tt]=j;}}vector<int> res;if(tt==n-1){for(int i=0;i<n;i++) res.push_back(q[i]);}return res;}bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {init();for(int i=0;i<prerequisites.size();i++){int a=prerequisites[i][1];int b=prerequisites[i][0];add(a,b);}if(bfs(numCourses).size()==0) return false;return true;}
};
3. Trie(前缀树)
- 实现Trie(前缀树) https://leetcode.cn/problems/implement-trie-prefix-tree/?envType=study-plan-v2&id=top-100-liked
typedef struct Node{struct Node* letter[26];bool isEnd; //表明这个节点对应的字母是不是某个单词的结尾
} Trie;//一个Trie表示树中的一个节点(一个字母),需要存储对应的数据结构表明:1.这个节点的所有儿子有哪些字母(即如果已存了单词abc,ads,则a的所有儿子为b和d)2.这个节点是否是某个单词的结束字母//初始化节点,不一定是树根
Trie* trieCreate() {Trie* p=(Trie*)malloc(sizeof(Trie));memset(p->letter,NULL,sizeof(p->letter));p->isEnd=false; //初始化一律为falsereturn p;
}void trieInsert(Trie* obj, char * word) {for(int i=0;word[i]!='\0';i++){if(obj->letter[word[i]-'a']){obj=obj->letter[word[i]-'a'];}else{obj->letter[word[i]-'a']=trieCreate();obj=obj->letter[word[i]-'a'];}}obj->isEnd=true;
}bool trieSearch(Trie* obj, char * word) {for(int i=0;word[i];i++){if(obj->letter[word[i]-'a']){ //说明树中有word[i]这个字符对应的节点, 可以接着往下搜索obj=obj->letter[word[i]-'a'];}else{ //树中没有相应节点, 说明word匹配失败, 直接返回falsereturn false;}}if(obj->isEnd) return true; //如果搜索停止的位置是一个单词的结尾return false;
}bool trieStartsWith(Trie* obj, char * prefix) {for(int i=0;prefix[i];i++){if(obj->letter[prefix[i]-'a']){ //说明树中有word[i]这个字符对应的节点, 可以接着往下搜索obj=obj->letter[prefix[i]-'a'];}else{ //树中没有相应节点, 说明word匹配失败, 直接返回falsereturn false;}}return true; //与trieSearch略有不同, 因为求的是前缀, 所以无所谓停止位置是不是这个单词的结尾, 直接返回true就行
}void trieFree(Trie* obj) {obj=trieCreate();
}/*** Your Trie struct will be instantiated and called as such:* Trie* obj = trieCreate();* trieInsert(obj, word);* bool param_2 = trieSearch(obj, word);* bool param_3 = trieStartsWith(obj, prefix);* trieFree(obj);
*/
相关文章:
)
图论专题(一)
图论专题(一) 参考文献 BFS和DFS的直观解释 https://blog.csdn.net/c406495762/article/details/117307841Leetcode岛屿问题系列分析 https://blog.csdn.net/qq_39144436/article/details/124173504多源广度优先 https://blog.csdn.net/peko1/article/details/121989497拓扑排…...

新星计划2023【网络应用领域基础】————————Day4
常见的网络基础介绍 前言 我们学习了一些基础的网络协议,以及子网掩码和vlan,同时也做了个简单的单臂路由实验 这篇文章我将仔细的讲解单臂路由的应用和交换机二层接口类型,以及wireshark的教程。 一,交换机二层接口 交换机的二…...

[CTF/网络安全] 攻防世界 view_source 解题详析
[CTF/网络安全] 攻防世界 view_source 解题详析 查看页面源代码方式归类总结 题目描述:X老师让小宁同学查看一个网页的源代码,但小宁同学发现鼠标右键好像不管用了。 查看页面源代码方式归类 单击鼠标右键,点击查看页面源代码: …...

目前流行的9大前端框架
1. React 2. Vue 3. Angular 、 4. Svelte 官网:https://svelte.dev 中文官网:https://www.sveltejs.cn Svelte 是一种全新的构建用户界面的方法。传统框架如 React 和 Vue 在浏览器中需要做大量的工作,而 Svelte 将这些工作放到构建应用程…...

【mysql】explain执行计划之select_type列
目录 一、说明二、示例2.1 simple:简单表,不使用union或者子查询2.2 primary:主查询,外层的查询2.3 subquery:select、where之后包含了子查询,在select语句中出现的子查询语句,结果不依赖于外部…...
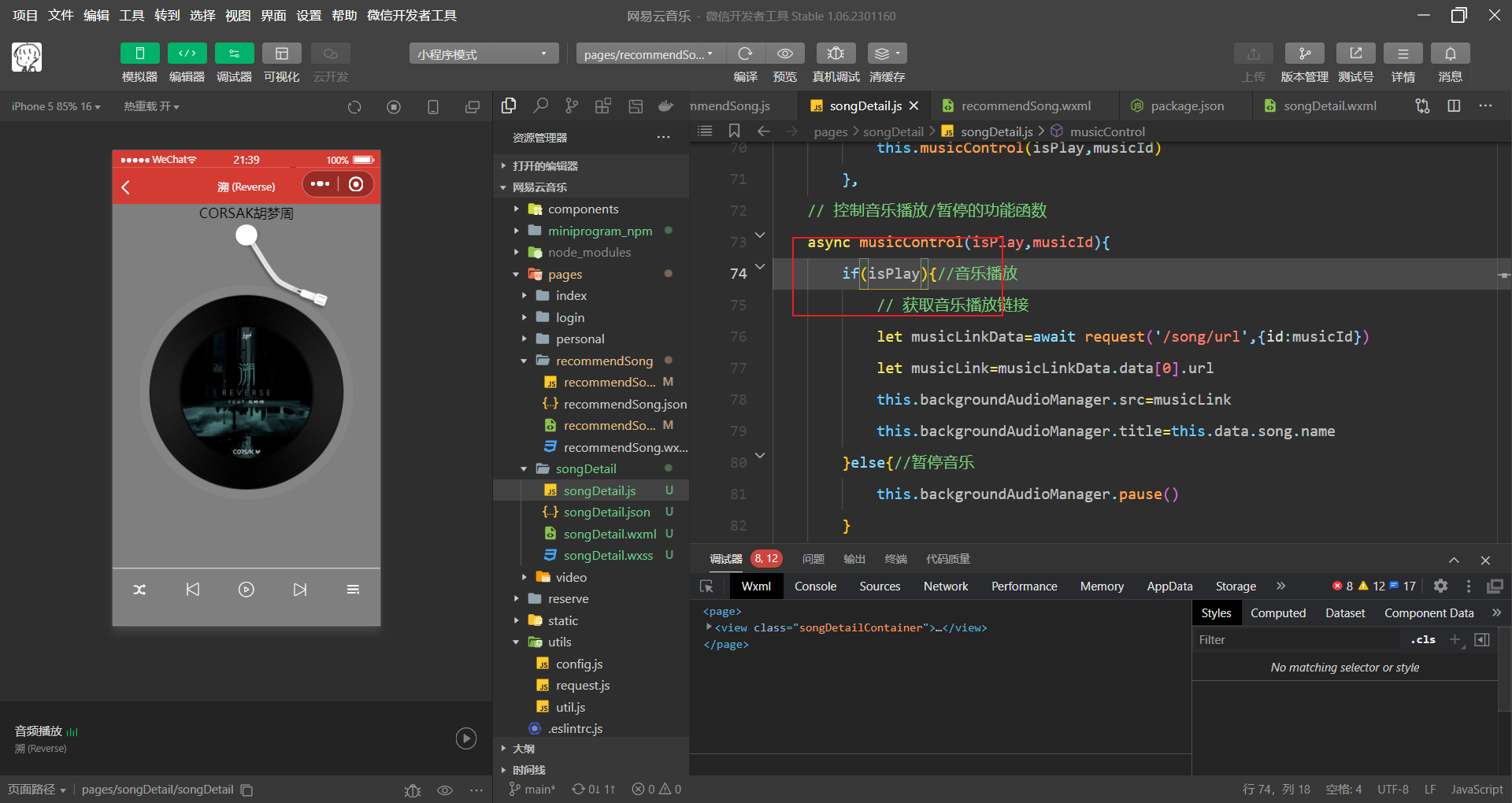
网易云音乐开发--音乐播放暂停切换上下首功能实现
音乐播放暂停功能实现 封装一个控制音乐播放/暂停的功能函数 看一下文档,我需要用的api 这个接口好像没有音频的url,查看一下,换个api 这样就能拿到id,并可以播放了 但是音乐并没有播放 我们少了这个 现在可以播放了ÿ…...

如何学习网络安全?
近半年我一直在整理网络安全相关资料,对于网络安全该怎么入门我谈谈我的看法,网络安全一直处于法律的边缘,学的不好或者剑走偏锋一下子人就进去了,所以我建议入门前先熟读《网络安全法》,除此之外还有《互联网安全产品…...

软件测试适合女生吗?
大家好,我是程序员馨馨,一个混过大厂,待过创业公司,有着 6 年工作经验的软件测试妹纸一枚。之前在也写过几篇文章,之后很多朋友过来咨询女生能不能做软件测试。 今天索性写篇文章,详细的介绍一下软件测试&a…...
华为云——代码托管的使用
一、打开前后端项目 登录华为云,点击页面右上角的用户名——点击个人设置 2.点击代码托管的HTTPS密码管理,设置自己的密码 3.回到代码仓库,复制HTTP地址 4.打开GitHubDesktop,点击左上角进行仓库克隆 (我这里已经cl…...

ChatGPT从⼊⻔到精通
编者寄语 ChatGPT 作为⼀种强⼤的⾃然语⾔处理模型,已经成为人工智能领域的重要研究⽅向之⼀。在不断的发展和创新 中,ChatGPT 已经具备了很强的⾃然语⾔处理能⼒,其可以实现⾃然语⾔的⽣成、理解和交互,为⼈类的⽣产和⽣活带来了…...
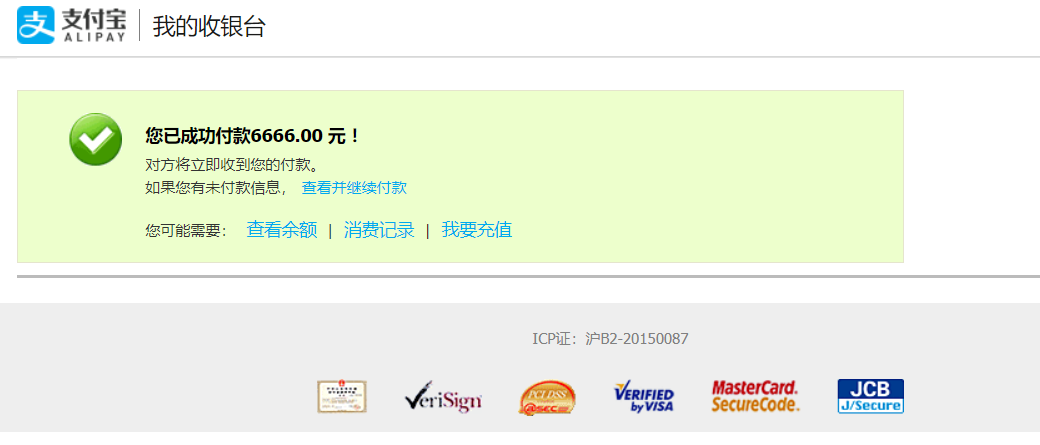
node + alipay-sdk 沙箱环境简单测试电脑网站支付
正式上线需要上传营业执照,不知道怎么去申请一个。。。。。 使用沙箱测试,首先前往支付宝开放平台控制台可看到左下方的沙箱测试链接: 然后设置接口加签方式,选择系统默认密钥: 系统默认密钥 -> 公钥模式 -> 查看…...
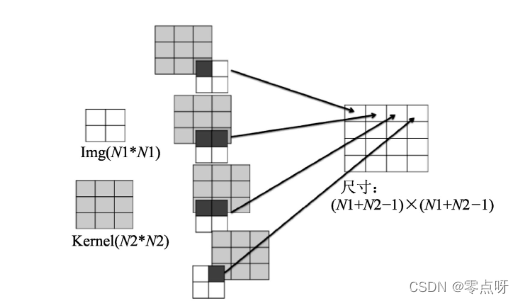
卷积神经网络详解
(一)网络结构 一个卷积神经网络里包括5部分——输入层、若干个卷积操作和池化层结合的部分、全局平均池化层、输出层: ● 输入层:将每个像素代表一个特征节点输入进来。 ● 卷积操作部分:由多个滤波器组合的卷积层。 …...
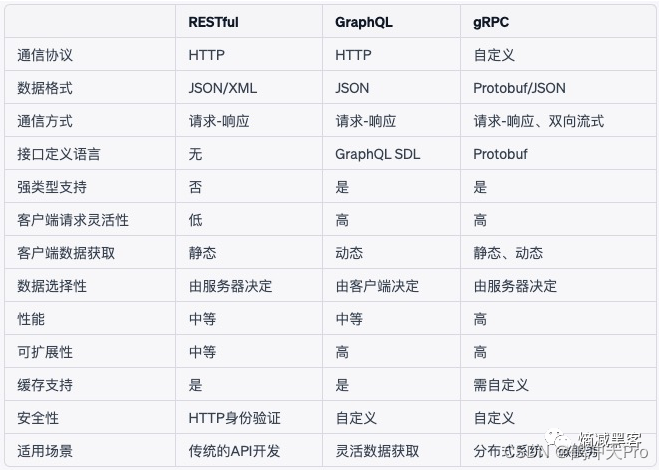
API架构的选择,RESTful、GraphQL还是gRPC
文章目录 一、RESTful1、什么是RESTful?2、RESTful架构的原则3、RESTful的适用场景4、RESTful的优点5、RESTful的缺点 二、GraphQL1、什么是GraphQL?2、GraphQL的原则3、GraphQL的优点4、GraphQL的缺点 三、gRPC1、什么是gRPC2、gRPC的应用场景3、gRPC的…...

人机融合智能的测量、计算与评价
老子在《道德经》第二十一章写道:"道之为物,惟恍惟惚。惚兮恍兮,其中有象;恍兮惚兮,其中有物。窈兮冥兮,其中有精;其精甚真,其中有信。"(“道”这个东西,没有清楚的固定实体。它是那样的恍恍惚惚啊,其中却有形象。它是那样的恍恍惚…...

虹科新品 | 高可靠性、可适用于高磁/压的线性传感器!
PART 1 什么是线性传感器? 基本上,线性传感器是一种用于测量位移和距离的设备,具有高可靠性。测量网格通过光学传感器移动测量数据,数据被光学记录并通过控制器转换为电气数据,而控制器又可以转换为路径。 因此&…...
支付系统设计五:对账系统设计01-总览
文章目录 前言一、对账系统构建二、执行流程三、获取支付渠道数据1.接口形式1.1 后台配置1.2 脚本编写1.2.1 模板1.2.2 解析脚本 2.FTP形式2.1 后台配置2.2 脚本编写2.2.1 模板2.2.2 解析脚本 四、获取支付平台数据五、数据比对1. 比对模型2. 比对器 总结 前言 从《支付系统设…...

阿里三面过了,却无理由挂了,HR反问一句话:为什么不考虑阿里?
进入互联网大厂一般都是“过五关斩六将”,难度堪比西天取经,但当你真正面对这些大厂的面试时,有时候又会被其中的神操作弄的很是蒙圈。 近日,某位测试员发帖称,自己去阿里面试,三面都过了,却被…...
办公智慧化风起云涌,华为MateBook X Pro 2023是最短距离
今年以来,我们几乎每个月,甚至每星期都可以看到大模型应用,在办公场景下推陈出新。 办公智慧化已成必然,大量智力工作正在被自动化。一个普遍共识是:AI能力范围之内的职业岌岌可危,AI 能力范围之外的职业欣…...

分布式项目 09.服务器之间的通信和三个工具类
项目的结构:1.通过Nginx首先把访问首页的请求发送到前端web服务器,2.web服务器会根据请求的url中的一些细节,来把相关的请求发送到相关的服务器中,3.相关的服务器会处理业务,并且返回结果到web服务器中,最后…...

C# 基本语法
C# 基本语法 C# 是一种面向对象的编程语言。在面向对象的程序设计方法中,程序由各种相互交互的对象组成。相同种类的对象通常具有相同的类型,或者说,是在相同的 class 中。 例如,以 Rectangle(矩形)对象为…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...
