【数据结构】散列表(哈希表)
文章目录
- 前言
- 一、什么是散列表
- 二、什么是哈希函数
- 三、下面简单介绍几种哈希函数
- 四、冲突
- 处理散列冲突的方法
- 开放定址法
- 再散列函数法
- 公共溢出区法
- 链地址法
- 五、代码实现
- 1.哈希函数
- 2.链表和哈希表的创建
- 3.哈希表初始化
- 3.从哈希表中根据key查找元素
- 4.哈希表插入元素
- 5.元素删除
- 6.哈希表销毁
前言
让我们想一下,若在手机通信录中查找一个人,那我们应该不会从第 1 个人一直找下去,因为这样实在是太慢了。我们其实是这样做的:首先看这个人的名字的首字母是什么,比如姓张,那么我们一定会滑到最后,因为“Z”姓的名字都在最后。
还有在查字典时,要查找一个单词,肯定不会从头翻到尾,而是首先通过这个单词的首字母,找到对应的那一页;再找第 2 个字母、第 3 个字母……这样可以快速跳到那个单词所在的页。
其实这里就用到了散列表的思想。
一、什么是散列表
散列表(hash table),我们平时叫它哈希表或者Hash 表,你肯定经常听到它。
散列表是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
由定义我们可以知道,散列表用的是数组支持下标访问数据的特性,所以散列表是数组的一种扩展,有数组演化而来。
二、什么是哈希函数
哈希函数就是将键转化为数组索引的过程,这个函数应该易于计算且能够均与分布所有的键。
三、下面简单介绍几种哈希函数
- 直接寻址法:取关键字或关键字的某个线性函数值为散列地址。
- 数字分析法:通过对数据的分析,发现数据中冲突较少的部分,并构造散列地址。例如同学们的学号,通常同一届学生的学号,其中前面的部分差别不太大,所以用后面的部分来构造散列地址。
- 平方取中法:当无法确定关键字里哪几位的分布相对比较均匀时,可以先求出关键字的平方值,然后按需要取平方值的中间几位作为散列地址。这是因为:计算平方之后的中间几位和关键字中的每一位都相关,所以不同的关键字会以较高的概率产生不同的散列地址。
- 取随机数法:使用一个随机函数,取关键字的随机值作为散列地址,这种方式通常用于关键字长度不同的场合。
- 除留取余法:取关键字被某个不大于散列表的表长 n 的数 m 除后所得的余数 p 为散列地址。这种方式也可以在用过其他方法后再使用。该函数对 m 的选择很重要,一般取素数或者直接用 n。
以上方法是对数字类型的操作,对字符串类型的数据,可以选择通过相加或者进位转化成数字后,再执行上面的计算方法。
四、冲突
冲突就是,两个不同的关键字,但是通过散列函数得出来的地址是一样的。
key1 ≠ key2,但是f(key1)= f(key2)
同义词
此时的key1 和key2就被称为这个散列函数的同义词
那可不行啊,一件单人间怎么可以住两个人呢?
别担心,这个问题自然已经被神通广大的大佬们解决了。
处理散列冲突的方法
开放定址法
开发定址法就是一旦发生了冲突,就去寻找下一个空的散列地址,只需要散列表足够大,空的散列地址总能找到,并将记录存入
例子:
19 01 23 14 55 68 11 86 37
要存储在表长11的数组中,其中H(key)=key MOD 11
- 线性探测法
公式
f1(key) = (f(key)+d1) MOD m(di=1,2,3,....,m-1)
我们取di等于1
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| key | 55 | 1 | 14 | 19 | 86 | ||||||
| 23冲突 | 23 | ||||||||||
| 68冲突 | 68冲突 | 68 | |||||||||
| 11冲突 | 11冲突 | 11冲突 | 11冲突 | 11冲突 | 11 | ||||||
| 37冲突 | 37冲突 | 37 | |||||||||
| 最终存储结果 | 55 | 1 | 23 | 14 | 68 | 11 | 37 | 19 | 86 |
- 二次探测法
增加平方运算的目的是为了不让关键字都聚再某一块区域,我们称这种方法为二次探测法
公式:
f1(key) = (f(key)+d1) MOD m(di=1^2,-1^2,2^2,-2^2,...,q^2,-q^2,q<=m/2)
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| key | 55 | 1 | 14 | 19 | 86 | ||||||
| 23冲突 | f(23)+1 | ||||||||||
| f(68)-1冲突 | 68冲突 | f(68)+1冲突 | f(68)+4 | ||||||||
| 11冲突 | f(11)+1冲突 | f(11)-1 | |||||||||
| 最终存储结果 | 55 | 1 | 23 | 14 | 68 | 19 | 86 | 11 |
- 随机探测法
在冲突时,对于位移量di采用随机函数计算得到,我们称之为随机探测法
公式
f1(key) = (f(key)+d1) MOD m(di是一个随机数列)
具体方法和上面一样
就不多赘述了
再散列函数法
对于我们的散列表来说,我们事先需要准备多个散列函数
f(key)=RHi(key) (i=1,2...,3)
这里的RHi就是不同的散列函数,每当发生冲突时,就换一个散列函数进行计算,总有一个函数可以将冲突解决
公共溢出区法
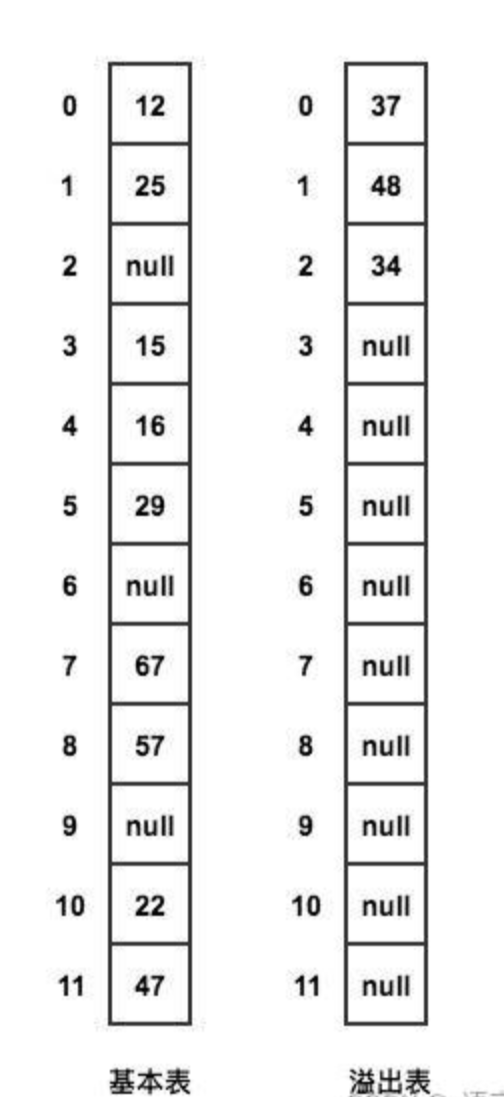
在原先基础表的基础上再添加一个溢出表
当发生冲突时,就将该数据放到溢出表中
在查找时,对给定值通过散列函数计算出散列地址后,先与基本表的相应位置进行对比,如果相等就查找成功,如果不相等,则到溢出表进行顺序查找
链地址法
就时用链表将发生冲突的数据链起来,在查找时,只需要遍历链表即可
如下图
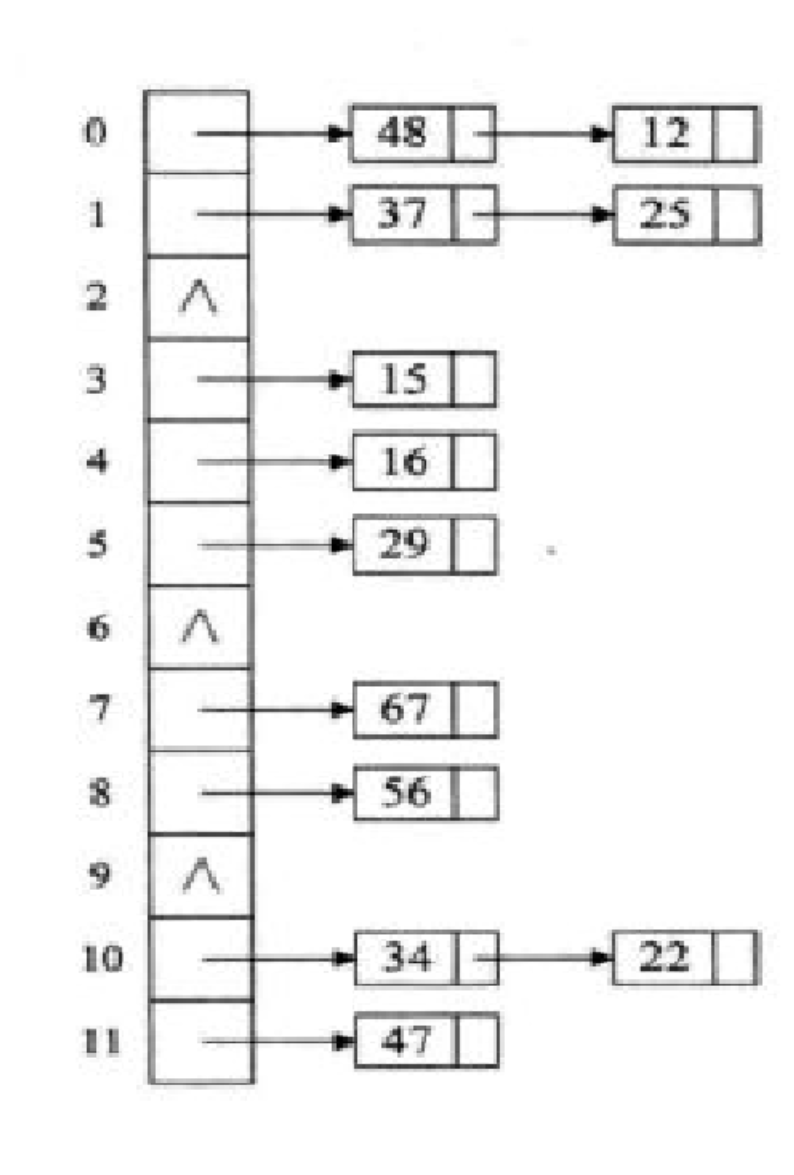
此方法也是我们最长用处理哈希冲突的方法
五、代码实现
1.哈希函数
//哈希函数
int Hash(int key, int TableSize)
{return key % TableSize;
}
2.链表和哈希表的创建
#define DEFAULT_SIZE 16
typedef int type;
//结点
typedef struct ListNode
{struct ListNode* next;int key; //线索type* data; //数据
}ListNode;
//提高可读性
typedef ListNode* List;
typedef ListNode* Element;
//哈希表
typedef struct HashTable
{int TableSize;List* Thelists;
}HashTable;
3.哈希表初始化
HashTable* InitHash(int TableSize)
{int i = 0;HashTable* htable = NULL;if (TableSize <= 0){TableSize = DEFAULT_SIZE;}htable = (HashTable*)malloc(sizeof(HashTable));if (htable == NULL){printf("初始化失败\n");return NULL;}//为桶分配内存空间,其为一个指针数组htable->Thelists = (List*)malloc(sizeof(List) * TableSize);if (htable->Thelists == NULL){printf("初始化失败\n");free(htable);return NULL;}//为Hash桶对应的指针数组初始化链表结点for (i = 0; i < TableSize; i++){htable->Thelists[i] = (ListNode*)malloc(sizeof(ListNode));if (htable->Thelists[i] == NULL){printf("初始化失败\n");free(htable->Thelists);free(htable);return NULL;}}
}
3.从哈希表中根据key查找元素
Element Find(HashTable* HashTable, int key)
{int i = 0;List L = NULL;Element e = NULL;i = Hash(key, HashTable->TableSize);L = HashTable->Thelists[i];e = L->next;while (e != NULL && e->key != key)e = e->next;return e;
}
4.哈希表插入元素
void Insert(HashTable* HashTable, int key, type* value)
{Element e = NULL, temp = NULL;List L = NULL;e = Find(HashTable, key);if (e == NULL){temp = (Element)malloc(sizeof(ListNode));if (temp == NULL){printf("malloc error\n");return;}L = HashTable->Thelists[Hash(key, HashTable->TableSize)];temp->data = value;temp->key = key;L->next = temp;}elseprintf("the key already exist\n");
}
5.元素删除
void Delete(HashTable* HashTable, int key)
{Element e = NULL, last = NULL;List L = NULL;int i = Hash(key, HashTable->TableSize);L = HashTable->Thelists[i];last = L;e = L->next;while (e != NULL && e->key != key){last = e;e = e->next;}if (e){last->next = e->next;free(e); }else{printf("该元素不存在\n");}
}
6.哈希表销毁
void Destory(HashTable* HashTable)
{int i = 0;List L = NULL;Element cur = NULL, next = NULL;for (i = 0; i < HashTable->TableSize; i++){L = HashTable->Thelists[i];cur = L->next;while (cur->next != NULL){next = cur->next;free(cur);cur = next;}}
相关文章:

【数据结构】散列表(哈希表)
文章目录 前言一、什么是散列表二、什么是哈希函数三、下面简单介绍几种哈希函数四、冲突处理散列冲突的方法开放定址法再散列函数法公共溢出区法链地址法 五、代码实现1.哈希函数2.链表和哈希表的创建3.哈希表初始化3.从哈希表中根据key查找元素4.哈希表插入元素5.元素删除6.哈…...
Flutter 笔记 | Flutter 核心原理(一)架构和生命周期
Flutter 架构 简单来讲,Flutter 从上到下可以分为三层:框架层、引擎层和嵌入层,下面我们分别介绍: 1. 框架层 Flutter Framework,即框架层。这是一个纯 Dart实现的 SDK,它实现了一套基础库,自…...
【Linux进阶之路】基本指令(下)
文章目录 一. 日志 date指令——查看日期基本语法1基本语法2cal指令——查看日历常见选项 二 .find——查找文件常用选项-name显示所有文件显示指定类型的文件 三.grep——行文本过滤工具语法常见的用法补充知识——APP与服务器的联系 四.打包压缩与解压解包zip与unzipzipunzip…...
Vue--》Vue 3 路由进阶——从基础到高级的完整指南
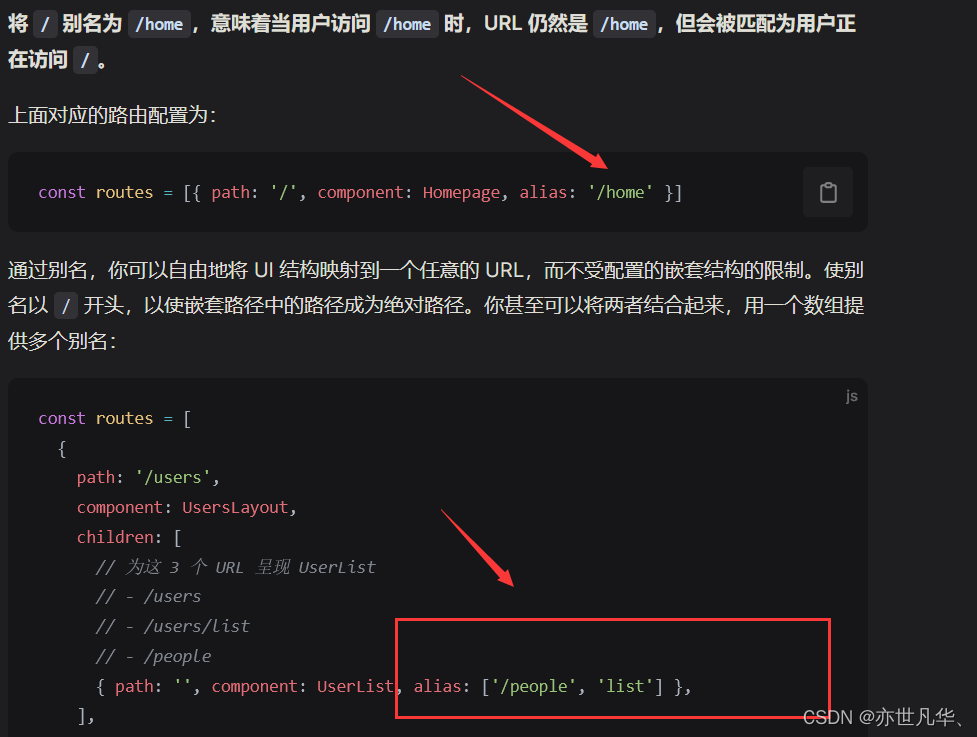
目录 Vue3中路由讲解与使用 路由的安装与使用 路由模式的使用 编程式路由导航 路由传参 嵌套路由 命名视图 重定向与别名 Vue3中路由讲解与使用 Vue 路由是 Vue.js 框架提供的一种机制,它用于管理网页上内容的导航。Vue 路由可以让我们在不刷新页面的情况下…...
【2022 Q4 | 100分】)
【华为OD机试真题】【python】 网上商城优惠活动(一)【2022 Q4 | 100分】
华为OD机试- 题目列表 2023Q1 点这里!! 2023华为OD机试-刷题指南 点这里!! 题目描述 某网上商场举办优惠活动,发布了满减、打折、无门槛3种 优惠券,分别为: 1:每满100元优惠10元,无使用数限制,如100~199元可以使用1张减10元,200-299可使用2张减20元,以此类推; 2:…...
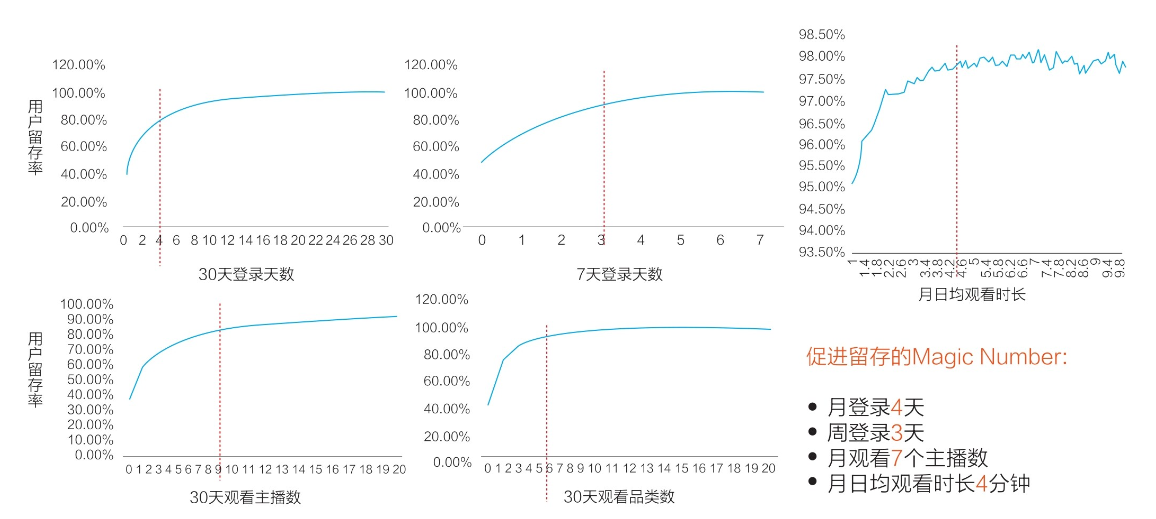
【业务数据分析】—— 用户留存分析(以挖掘Aha时刻为例)
目录 一、用户留存是什么 二、为什么要考虑用户留存 1、为什么要考虑用户留存? 2、影响用户留存的可能因素 3、用户留存的3个阶段 三、怎么进行用户留存分析(挖掘Aha时刻) 1、Aha时刻 2、Aha时刻的作用 3、挖掘Aha时刻 一、用户留存是什么 在互联网行业中&…...

极客的git常用命令手册
极客的git常用命令手册 1.1 权限配置篇1.1.1 创建ssh key1.1.2 本地存在多个密钥时,如何根据目标平台自动选择用于认证的密钥? 1.2 基础信息配置篇1.2.1 配置用户名1.2.2 配置用户邮箱1.2.3 设置文件名大小写区分1.2.4 设置命令行显示颜色1.2.5 检查git全…...
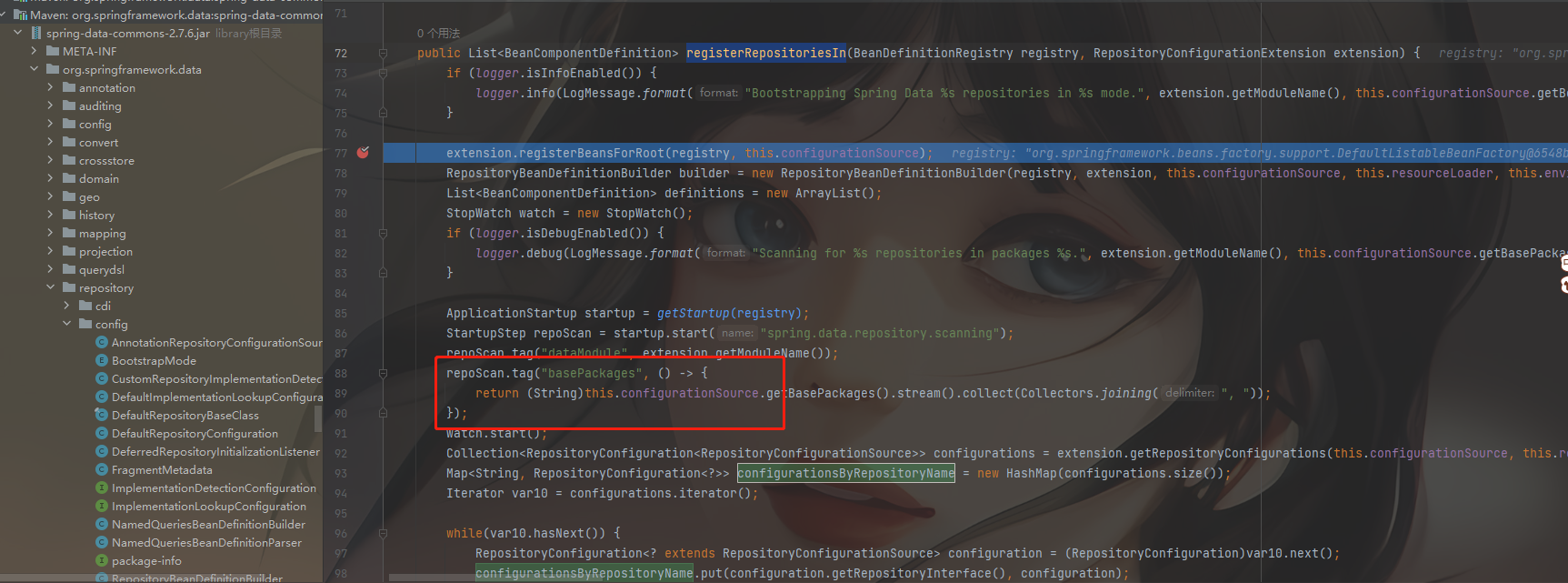
spring-data 一统江湖,玩转多种数据源
1、起因 因为要在项目中同时访问redis,mongo和mysql三种数据库,而且因为偏向spring-data,所以都使用了spring-data 在使用的过程中如果不做配置发现会有冲突,这篇文章也是解决这个问题,避免以后遇到同样的问题不知所…...
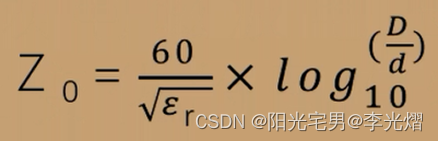
【EMC专题】为什么PCB上的单端阻抗控制在50欧?
每当我们在发板后和PCB板厂沟通说有些走线需要阻抗控制,控制在多少多少。其实我们所说的阻抗是传输线的特性阻抗。特性阻抗是不能用万用表测量出来的,他由传输线的结构以及材料决定,与传输线的长度、信号的幅度、频率等均无关。 特性阻抗的概念 当电磁波在电缆上…...
想自学写个操作系统,有哪些推荐看的书籍?
前言 哈喽,我是子牙,一个很卷的硬核男人。喜欢研究底层,聚焦做那些大家想学没地方学的课程:手写操作系统、手写虚拟机、手写编程语言… 今天我们将站在一个自学者的角度来聊聊如何实现自己的操作系统。并为大家推荐几本能够帮助你…...
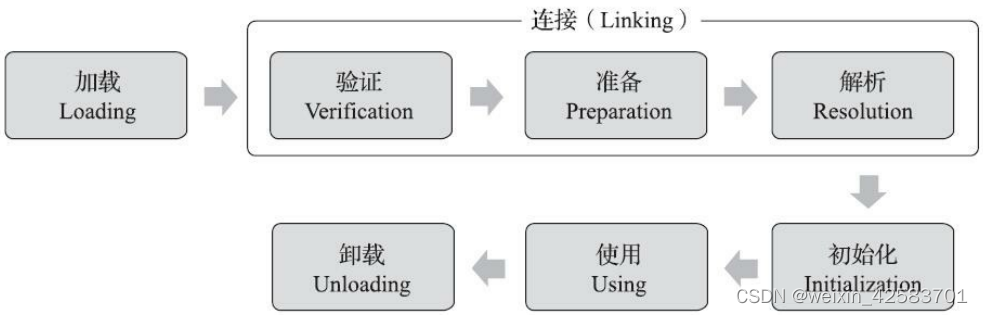
深入理解Java虚拟机:JVM高级特性与最佳实践-总结-7
深入理解Java虚拟机:JVM高级特性与最佳实践-总结-7 类文件结构概述无关性的基石 虚拟机类加载机制概述类加载的时机 类文件结构 代码编译的结果从本地机器码转变为字节码,是存储格式发展的一小步,却是编程语言发展的一大步 概述 我们写的程…...
ES6中flat与flatMap使用
1、方法介绍 数组的成员有时还是数组,Array.prototype.flat()用于将嵌套的数组“拉平”,变成一维的数组。该方法返回一个新数组,对原数据没有影响。 [1, 2, [3, 4]].flat() // [1, 2, 3, 4]上面代码中,原数组的成员里面有一个数…...

苹果手机、电脑如何进行屏幕录制?苹果录屏功能在哪?
随着人们生活水平的提高,不少小伙伴都会选择苹果手机、苹果电脑作为主要的设备。因为使用苹果电脑进行办公,不仅仅能够提升效率,对于文件的安全性也是有一些保障的。那么,在使用苹果电脑的时候,如果需要有录屏的需求该…...

什么是研发 Lead Time?我悟了!
嗨,朋友!你听说过「新型工伤」吗? 我好像「赛博确诊」了😣 那天朋友约我吃饭,我下意识回复了句「好的,那我提一个日程」……还有上次跟一位准妈妈聊天,我好奇宝宝的预产期,结果脱口…...

android 窗口焦点介绍
背景 我们经常会遇到一种Application does not hava focused window的ANR异常,这种异常一般是没有焦点窗口FocusedWindow导致,且这类异常只会发生在key事件的派发,因为key事件是需要找到一个焦点窗口然后再派发,而触摸事件只需要找到当前显示…...

研发工程师玩转Kubernetes——构建、推送自定义镜像
这几节我们都是使用microk8s学习kubernetes,于是镜像库我们也是使用它的插件——registry。 开启镜像库插件 microk8s enable registry模拟开发环境 我们使用Python作为开发语言来进行本系列的演练。 安装Python sudo apt install python3.11安装Pip3 pip3用于…...

[网络安全]DVWA之XSS(Stored)攻击姿势及解题详析合集
[网络安全]DVWA之XSS(Stored)攻击姿势及解题详析合集 XSS(Stored)-low level源代码姿势基于Message板块基于Name板块 XSS(Stored)-medium level源代码姿势双写绕过大小写绕过Xss标签绕过 XSS(Stored)-high level源代码姿势:Xss标签绕过 XSS(S…...
 A~D1)
VP记录:Codeforces Round 873 (Div. 2) A~D1
传送门:CF 前题提要:因为本场比赛的D题让我十分难受.刚开始以为 r − l 1 r-l1 r−l1与 r − l r-l r−l应该没什么不同.但是做的时候发现假设是 r − l 1 r-l1 r−l1的话我们可以使用线段树来维护,但是 r − l r-l r−l就让线段树维护的难度大大增加,这导致我十分烦躁,所以…...

【C++】函数提高
欢迎来到博主 Apeiron 的博客,祝您旅程愉快 !时止则止,时行则行。动静不失其时,其道光明。 目录 1、缘起 2、函数默认参数 3、函数占位参数 4、总结 1、缘起 以前学习过了函数的基本用法和功能,现在是时候学习函数…...

【可持续能源:让我们迈向绿色、可持续未来的道路】
作为未来的主要能源来源,可持续能源技术确实有潜力改变我们的世界。随着全球对传统化石燃料的依赖程度逐渐降低,可再生能源已成为许多国家推进能源转型的首选。 从太阳能和风能到地热能和潮汐能,可持续能源技术已经在许多方面取得了重大突破…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...
