VP记录:Codeforces Round 873 (Div. 2) A~D1
传送门:CF
前题提要:因为本场比赛的D题让我十分难受.刚开始以为 r − l + 1 r-l+1 r−l+1与 r − l r-l r−l应该没什么不同.但是做的时候发现假设是 r − l + 1 r-l+1 r−l+1的话我们可以使用线段树来维护,但是 r − l r-l r−l就让线段树维护的难度大大增加,这导致我十分烦躁,所以就不想做本场比赛的D2了
A题:A. Divisible Array
一道构造题.因为需要被下标整除,所以我们不妨直接将每一位的数字赋值成该下标,但是我们发现这样子的总和将会是 ( n + 1 ) ∗ n / 2 (n+1)*n/2 (n+1)∗n/2这样不一定被 n n n整除,但是此时我们只要将整体乘一个 2 2 2就可以了.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int main() {int T=read();while(T--) {int n=read();for(int i=1;i<=n;i++) {cout<<2*i<<" ";}cout<<endl;}return 0;
}
B题:B. Permutation Swap
把玩一下题意之后不难发现.我们的 a [ i ] a[i] a[i]最终是要移动到下标为 a [ i ] a[i] a[i]的位置.那么我们需要移动的总距离就是 a b s ( a [ i ] − i ) abs(a[i]-i) abs(a[i]−i).诶,此时我们想一下有多少种 k k k将会满足此次移动,我们会发现 k k k需要满足是 a b s ( a [ i ] − i ) abs(a[i]-i) abs(a[i]−i)的因子才行.
所以此时我们只要对所有的 a b s ( a [ i ] − i ) abs(a[i]-i) abs(a[i]−i)取一个 g c d gcd gcd就行了.
但是有一个细节需要注意,就是当我们的 a [ i ] a[i] a[i]就处于 a [ i ] a[i] a[i]的位置的时候,此时任意的 k k k对于该数字都是满足的,所以此时我们不需要管这个数字即可
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int gcd(int a,int b) {if(a%b==0) return b;else return gcd(b,a%b);
}
int a[maxn];
int main() {int T=read();while(T--) {int n=read();for(int i=1;i<=n;i++) a[i]=read();vector<int>b;for(int i=1;i<=n;i++) {int num=abs(a[i]-i);if(num==0) continue;else b.push_back(num);}int ans=b[0];for(int i=1;i<b.size();i++) {ans=gcd(ans,b[i]);}cout<<ans<<endl;}return 0;
}
C. Counting Orders
考虑对两个数组进行一个排序(从小到大).然后此时我们的两个数组应该满足所有的 a [ i ] < b [ i ] a[i]<b[i] a[i]<b[i].不然我们的答案就是0.下面简单证明一下这个结论:
假设此时我们的答案不为0.那么我们将需要处理一下 a [ i ] > b [ i ] a[i]>b[i] a[i]>b[i]的那一个数字.我们发现想要处理这个数字,我们就需要将后面的 i i i后面的数字换到 i i i位置.那么也就是将 i i i换到后面去才能满足题意.但是我们发现两个数组都是单调增的.此时我们的 a [ i ] a[i] a[i]已经偏小了,换到后面去不是更为偏小,所以是不可能满足题意的(还有一种情况是先与i前面的换,再将前面的换到后面,这种情况显然也是不行的)
那么此时我们考虑在这个的基础上算出最后的答案.考虑对于每一位的 a [ i ] a[i] a[i],我们先算出他能放在哪些位置,不难发现可以在b数组中用二分找到第一个大于 a [ i ] a[i] a[i]的位置,不妨记为 p o s 1 pos1 pos1(注意,b数组是单调的).那么此时我们可以放的位置显然就是 p o s − 1 pos-1 pos−1.我们继续找 a [ i + 1 ] a[i+1] a[i+1]的可放位置数,记为 p o s 2 pos2 pos2.我们会发现存在这样的一个性质,就是a[i]可以放的位置显然a[i+1]也是可以放的,并且a[i]会占用a[i+1]的一个可行位置.所以此时的总贡献就是:
∏ i = 1 n p o s i − ( i − 1 ) \prod\limits_{i=1}^n {pos_i-(i-1)} i=1∏nposi−(i−1)
至此本题也就不难解决了
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
#define int long long
const int mod=1e9+7;
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int n;vector<int>a,b;
signed main() {int T=read();while(T--) {n=read();a.clear();b.clear();for(int i=1;i<=n;i++) {int num=read();a.push_back(num);}for(int i=1;i<=n;i++) {int num=read();b.push_back(num);}sort(a.begin(),a.end());sort(b.begin(),b.end());int flag=0;for(int i=0;i<n;i++) {if(a[i]<=b[i]) {flag=1;break;} }if(flag) {cout<<0<<endl;continue;}int ans=1;for(int i=0;i<n;i++) {int pos=lower_bound(b.begin(),b.end(),a[i])-b.begin();ans=ans*(pos-i)%mod;}cout<<ans<<endl;} return 0;
}
D1:Range Sorting (Easy Version)
首先需要注意的是对于一个区间的花费是 r − l r-l r−l
然后我们发现对于一个位置的数字进行排序的花费是0.这就意味对于不需要排序的所有数字,我们也可以将其看做为对单个位置的数字进行排序!!.
然后我们考虑对于一个区间 [ l , r ] [l,r] [l,r],我们将其按照排序的区间来将其分块,举一个栗子:
1 , 2 , 4 , 3 1,2,4,3 1,2,4,3这样的区间,我们就将其分块为 1 2 4 , 3 1\;\;2\;\;4,3 124,3这三个区间,此时我们发现这样做的总贡献就是区间的长度减去块的个数!!,这个很好证明.因为我们的花费是 r − l r-l r−l,所以我们没分出一个新的块,我们的贡献就是当前的长度-1.我们将其累加一下就会发现区间的总贡献就是总区间的长度减去块的个数.
当然对于上述的结论,我们需要一个前题,“就是对于每一个排序区间,它们都不是相交的,也就是进行不相交的进行排序才是最优的”,这个不难证明,限于篇幅,此处就不在赘述了
所以我们现在的问题就变成了计算一个区间中的块的个数.我们发现每一个块内的数字显然是单调递减的(这个很重要).考虑使用单调栈来维护每一个块的最大值(维护的栈是单调增的,这个也很重要).假设当前枚举到了区间中的 a [ i ] a[i] a[i],我们此时的值小于前面的数字,我们就需要将 a [ i ] a[i] a[i]换到之前的位置,那么此时需要换到哪一个位置呢.我们发现当前数字假设比块的最大值要小,并且因为我们块中的数字是呈单调减排列的,所以此时我们的该数字应该是放在这个块前面才行,也就是说此时的排序区间的左端点要管到最大值的那一个位置.所以此时这个数字很显然就可以合并到之前的那一个块中.我们对此进行合并即可.
假设当前枚举到的数字比之前的最大值要大,那么此时这个数字比之前的所有数字都要大,这就意味着当前数字目前来说并不需要进行排序,所以我们将其独立作为一个块
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
#define int long long
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int a[maxn];
signed main() {int T=read();while(T--) {int n=read();for(int i=1;i<=n;i++) a[i]=read();int ans=0;for(int l=1;l<=n;l++) {stack<int>s;for(int len=1;l+len-1<=n;len++) {int r=l+len-1;int flag=1;int maxx=a[r];while(!s.empty()&&a[r]<s.top()) {if(flag==1){maxx=s.top();flag=0;}s.pop();}if(flag==0) s.push(maxx);else s.push(a[r]);ans+=len-s.size();}}cout<<ans<<endl;}return 0;
}
相关文章:
 A~D1)
VP记录:Codeforces Round 873 (Div. 2) A~D1
传送门:CF 前题提要:因为本场比赛的D题让我十分难受.刚开始以为 r − l 1 r-l1 r−l1与 r − l r-l r−l应该没什么不同.但是做的时候发现假设是 r − l 1 r-l1 r−l1的话我们可以使用线段树来维护,但是 r − l r-l r−l就让线段树维护的难度大大增加,这导致我十分烦躁,所以…...

【C++】函数提高
欢迎来到博主 Apeiron 的博客,祝您旅程愉快 !时止则止,时行则行。动静不失其时,其道光明。 目录 1、缘起 2、函数默认参数 3、函数占位参数 4、总结 1、缘起 以前学习过了函数的基本用法和功能,现在是时候学习函数…...

【可持续能源:让我们迈向绿色、可持续未来的道路】
作为未来的主要能源来源,可持续能源技术确实有潜力改变我们的世界。随着全球对传统化石燃料的依赖程度逐渐降低,可再生能源已成为许多国家推进能源转型的首选。 从太阳能和风能到地热能和潮汐能,可持续能源技术已经在许多方面取得了重大突破…...
ES6中数组新增了哪些扩展?
一、扩展运算符的应用 ES6通过扩展元素符...,好比 rest 参数的逆运算,将一个数组转为用逗号分隔的参数序列 console.log(...[1, 2, 3]) // 1 2 3console.log(1, ...[2, 3, 4], 5) // 1 2 3 4 5[...document.querySelectorAll(div)] // [<div>, …...

【算法】动态规划
一、基础知识 动态规划的基本思想:将待求解问题分解成若干个子问题,如果各个子问题不是独立的,不同的子问题的个数只是多项式量级,为避免大量的重复计算,用一个表记录所有已解决的子问题的答案,而在需要的…...

HNOI2014 世界树
洛谷P3233 [HNOI2014]世界树 题目大意 有一棵 n n n个点的树,每个点有一个编号,有 q q q次操作。对于每次操作,给出 m m m个点并称为议事点,树上各个点由离这个点最近的议事点管理(如果有多个议事点离这个点最近&…...

在MyBatis XML文件中处理特殊符号的方法,如“>”、“<”、“>=”、“<=”这些符号XML会报错如何处理
前言 在MyBatis的XML映射文件中,我们经常需要使用特殊符号,比如"大于"、"小于"、"大于等于"、"小于等于"等比较操作符。然而,这些符号在XML中具有特殊的含义,因此需要进行特殊处理&…...

第三章--第一篇:什么是对话系统?
对话系统是一种人机交互的技术,旨在使计算机能够与人类进行自然而流畅的对话。它是人工智能领域的重要研究方向,具有重要的实际应用价值和广泛的普适性。 首先,对话系统的重要性在于它可以提供高效便捷的人机交互方式。传统的人机界面,如图形用户界面(GUI)和命令行界面(…...

项目基础搭建
一、项目创建 1.下载并安装nodejs 下载完成后,查看node版本 winR 快捷键,cmd确定,进入后台黑框 node -v查看npm安装路径 npm root -g安装cnpm镜像 npm install -g cnpm --registryhttps://registry.npm.taobao.org:查看npm版…...

PFCdocumentation_FISH Rules and Usage
目录 FISH Scripting FISH Rules and Usage Lines Data Types Reserved Names for Functions and Variables Scope of Variables Functions: Structure, Evaluation, and Calling Scheme Arithmetic: Expressions and Type Conversions Redefining FISH Functions Ex…...
如何完美卸载VS2015(2023年5月份实测有效)
使用控制面板卸载VS2015,出现正在配置您的系统,这可能需要一些时间,然后就出现卡住半个小时第二行的条都没有动的问题,这里提供vs2015以及以前版本的卸载方式 问题产生原因:他需要下载一些东西,然后由于你懂的网络原因…...

JavaScript如何声明和定义函数
JavaScript是一门非常有趣的编程语言,它可以让我们创建各种各样的函数来解决各种各样的问题。在JavaScript中,函数的声明和定义非常重要,因为它们决定了函数的行为和执行过程。 首先,让我们来看看JavaScript中函数的声明。在Java…...

微信小程序 WebSocket 通信 —— 在线聊天
在Node栏目就讲到了Socket通信的内容,使用Node实现Socke通信,还使用两个流行的WebSocket 库,ws 和 socket.io,在小程序中的WebSocket接口和HTML5的WebSocket基本相同,可以实现浏览器与服务器之间的全双工通信。那么本篇…...
VMware快照:简化虚拟化环境管理与数据保护
引言: 在虚拟化环境中,数据保护和灵活性是至关重要的。VMware快照作为一项强大的功能,为虚拟机管理者提供了便利和安全性。本文将介绍VMware快照的使用,以及它为用户带来的几个关键优势。 VMware快照是一项重要的功能,…...
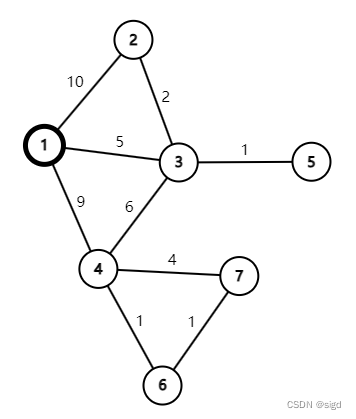
图的最短路径
最短路径算法对图结构没有特殊要求,不要求连通图,且有向图无向图均可。 最短路径算法目标是求得从某顶点出发,沿图的边到达另一顶点所经过的路径中,各边上权值之和最小的一条路径。解决最短路的问题有以下算法:Dijkst…...

RHCE----Shell变量和引用
1.变量的类型及含义 变量类型: 1、自定义变量: 在当前的shell命令行界面设置的变量是局部变量 例子: num1 namezhangsan 2、环境变量全局变量,通过export 导出后的局部变量是全局变量 、bash的初始化文件:/etc/profile:存放一些全局变量…...
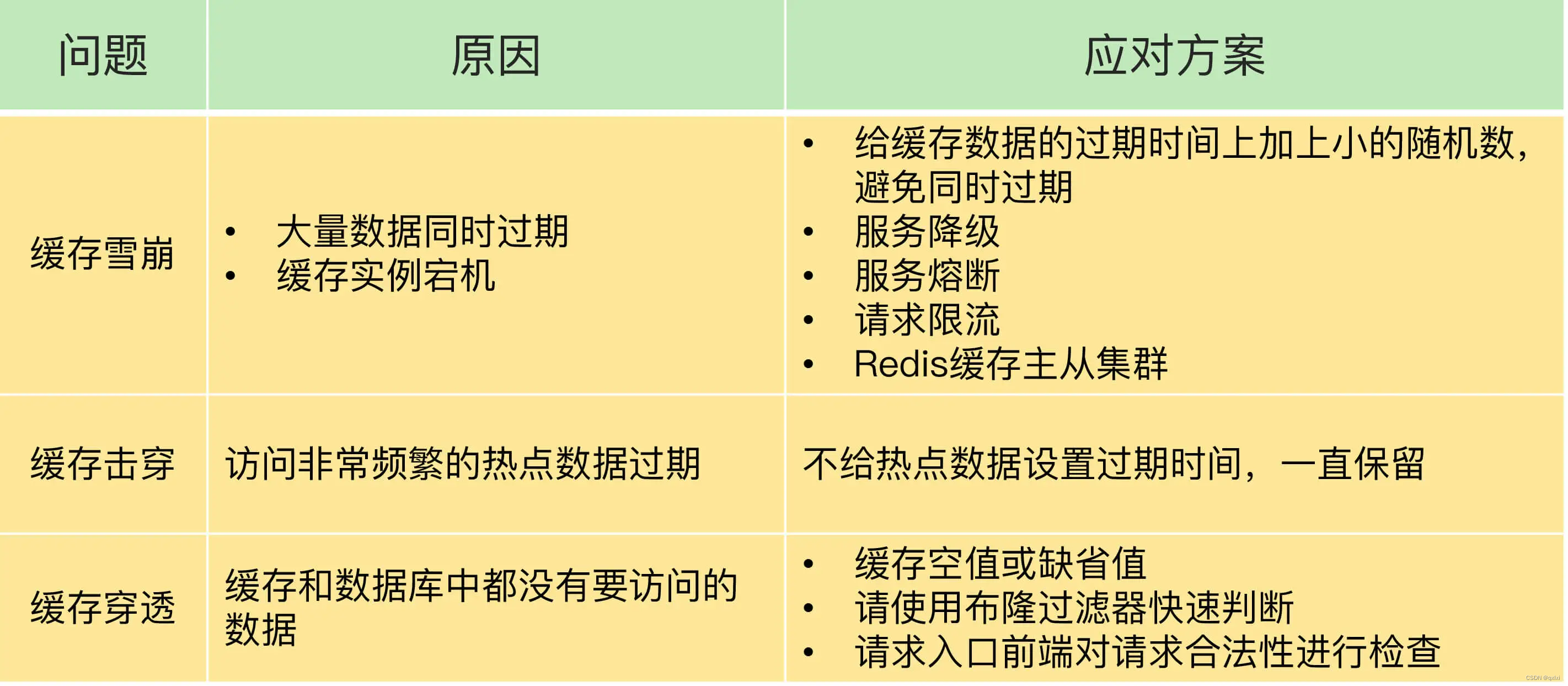
【Redis】聊一下缓存雪崩、击穿、穿透、预热
缓存的引入带来了数据读取性能的提升,但是因此也引入新的问题,一个是数据双写一致性,另一个就是雪崩、击穿、穿透,那么如何解决这些问题,我们来说下对应的问题和解决方案 雪崩 缓存雪崩:同一时间内大量请…...

全景描绘云原生技术图谱,首个《云原生应用引擎技术发展白皮书》发布
5月12日,由神州数码主办、北京经开区国家信创园、中关村云计算产业联盟协办的2023通明湖论坛-云原生分论坛在京召开。论坛期间,神州数码联合北京通明湖信息技术应用创新中心、中国信通院和通明智云正式发布了《云原生应用引擎技术发展白皮书》࿰…...
【Python共享文件】——Python快速搭建HTTP web服务实现文件共享并公网远程访问
文章目录 1. 前言2. 视频教程3. 本地文件服务器搭建3.1 python的安装和设置3.2 cpolar的安装和注册 4. 本地文件服务器的发布4.1 Cpolar云端设置4.2 Cpolar本地设置 5. 公网访问测试6. 结语 1. 前言 数据共享作为和连接作为互联网的基础应用,不仅在商业和办公场景有…...

Mysql数据库分库分表
为什么使用分库分表? 传统的将数据集中存储至单一数据节点的解决方案,在性能、可用性和运维成本这三方面已经难于满足互联网的海量数据场景。 1)性能 从性能方面来说,由于关系型数据库大多采用 B 树类型的索引,在数…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
