【算法】动态规划
一、基础知识
动态规划的基本思想:将待求解问题分解成若干个子问题,如果各个子问题不是独立的,不同的子问题的个数只是多项式量级,为避免大量的重复计算,用一个表记录所有已解决的子问题的答案,而在需要的时候再找出已求得的答案。
分治与动态规划算法的异同:
相似之处:
- 都可以将大问题划分为小问题求解。
- 都需要重叠子问题的最优解。
不同之处:
-
分治算法是自上而下,递归求解,然后合并结果。动态规划是自下而上,从更小的子问题开始递推。
-
分治算法对每个子问题只计算一次,不会重复计算。动态规划算法会存储每个子问题的解,重复使用,避免重复计算。
-
分治算法不需要存储中间结果,只存储最终结果。动态规划需要创建一个表来存储各个子问题的解。
-
分治算法对每个子问题的解需要进行合并,而动态规划只需要简单地查表即可得到解。
-
分治算法的时间复杂度较高,常为O(nlogn)。动态规划能达到O(n)的时间复杂度。
总之,分治算法采用自上而下的分解方式,只存储最终结果,要进行结果合并,效率较低。动态规划采用自下而上递推的方式,存储每个子问题的最优解,通过查表得到最终解,效率较高。
理解动态规划算法的基本要素:
- 最优子结构性质:问题的最优解包含了其子问题的最优解。
- 重叠子问题性质:有些子问题被反复计算多次。
动态规划算法求解问题的步骤:
- 找出最优解的性质,并刻画其结构特征
- 递归地定义最优值
- 以自底向上的方式计算出最优值
- 构造最优解
二、矩阵连乘问题




伪代码:
//用动态规划法求解
void MatrixChain(int *p,int n,int **m,int **s)
{for (int i = 1; i <= n; i++) m[i][i] = 0;//矩阵链长度为1for (int r = 2; r <= n; r++) //r为矩阵链长度,从2…nfor (int i = 1; i <= n - r+1; i++) {//遍历所有长度是r的子问题。//对于每一个给定的链长r,左边界为i,右边界为jint j=i+r-1;m[i][j] = +∞; s[i][j] = i;//记录断开位置,即加括号的位置for (int k = i; k < j; k++){//矩阵链的分隔位置从第i个矩阵…第j-1个矩阵int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];if (t < m[i][j]) { m[i][j] = t; s[i][j] = k;}}}
}
三、最长公共子序列问题




int LCSLength(char *x,char *y,int c[ ][N],int b[ ][N])
{ //x和y的长度 int m=strlen(x),n=strlen(y); int i,j; //初始化c[][] for (i = 0; i <= m; i++) c[i][0] = 0; for (i = 0; i <= n; i++) c[0][i] = 0; //计算c[][]for (i = 1; i <= m; i++) for (j = 1; j <= n; j++){//如果两个字符相同,左上方的值加1 if (x[i-1]==y[j-1]) { c[i][j]=c[i-1][j-1]+1; b[i][j]=1; } //如果不相同,取左方和上方的最大值 else if (c[i-1][j] >= c[i][j-1]) { c[i][j]=c[i-1][j]; b[i][j]=2; } else { c[i][j]=c[i][j-1]; b[i][j]=3; } } //返回最长公共子序列长度return c[m][n];
}
//通过b[][]回溯构造最长公共子序列
void LCS(int i,int j,char *x,int **b)
{ //到达边界,返回 if (i ==0 || j==0) return; //向左上方移动 if (b[i][j]== 1){ LCS(i-1,j-1,x,b); cout<<x[i]; } //向左方移动else if (b[i][j]== 2) LCS(i-1,j,x,b); //向上方移动else LCS(i,j-1,x,b);
}
四、最大子段和问题



int maxSum(int a[],int n,int &begin,int &end){int sum=0; //结果,最大子序列和int b=0; //当前和for(int i=0;i<n;i++){if(b>0) b+=a[i]; //如果b大于0,加上当前元素 else{ b=a[i]; //如果b等于0,重新开始,b赋值为当前元素值begin=i; //记录开始位置 }if(b>sum){ //如果当前和大于结果,更新结果和结尾位置 sum=b; end=i; } }return sum; //返回结果
} 五、0-1背包问题


int Knapsack(int v[], int w[], int c, int n, m[][])
{ //初始化第一行和第一列,均为0for(int i=0;i<=n;i++) m[i][0]=0; for(int j=0;j<=c;j++) m[0][j]=0; //自底向上计算每个子问题的最优值for(i=1;i<=n;i++) for(j=1;j<=c;j++){ //如果不能装下,最大价值就是不考虑该物品的价值if(j<w[i]) m[i][j]=m[i-1][j]; //如果能装下,取决于装入或不装入该物品的最大值elsem[i][j]=max(m[i-1][j], m[i-1][j-w[i]]+v[i]);} //返回总的最大价值return m[n][c];
}
相关文章:

【算法】动态规划
一、基础知识 动态规划的基本思想:将待求解问题分解成若干个子问题,如果各个子问题不是独立的,不同的子问题的个数只是多项式量级,为避免大量的重复计算,用一个表记录所有已解决的子问题的答案,而在需要的…...

HNOI2014 世界树
洛谷P3233 [HNOI2014]世界树 题目大意 有一棵 n n n个点的树,每个点有一个编号,有 q q q次操作。对于每次操作,给出 m m m个点并称为议事点,树上各个点由离这个点最近的议事点管理(如果有多个议事点离这个点最近&…...

在MyBatis XML文件中处理特殊符号的方法,如“>”、“<”、“>=”、“<=”这些符号XML会报错如何处理
前言 在MyBatis的XML映射文件中,我们经常需要使用特殊符号,比如"大于"、"小于"、"大于等于"、"小于等于"等比较操作符。然而,这些符号在XML中具有特殊的含义,因此需要进行特殊处理&…...

第三章--第一篇:什么是对话系统?
对话系统是一种人机交互的技术,旨在使计算机能够与人类进行自然而流畅的对话。它是人工智能领域的重要研究方向,具有重要的实际应用价值和广泛的普适性。 首先,对话系统的重要性在于它可以提供高效便捷的人机交互方式。传统的人机界面,如图形用户界面(GUI)和命令行界面(…...

项目基础搭建
一、项目创建 1.下载并安装nodejs 下载完成后,查看node版本 winR 快捷键,cmd确定,进入后台黑框 node -v查看npm安装路径 npm root -g安装cnpm镜像 npm install -g cnpm --registryhttps://registry.npm.taobao.org:查看npm版…...

PFCdocumentation_FISH Rules and Usage
目录 FISH Scripting FISH Rules and Usage Lines Data Types Reserved Names for Functions and Variables Scope of Variables Functions: Structure, Evaluation, and Calling Scheme Arithmetic: Expressions and Type Conversions Redefining FISH Functions Ex…...
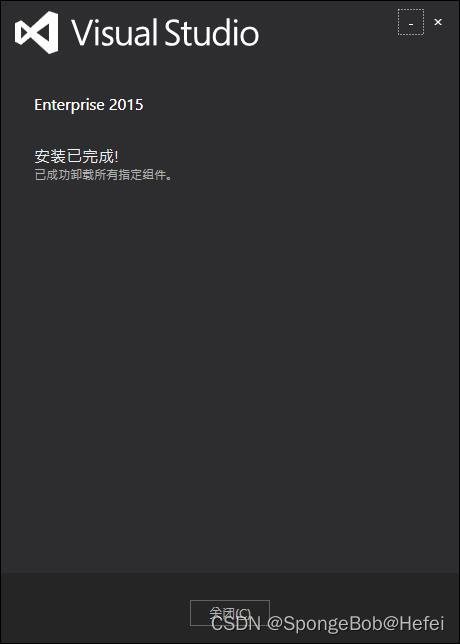
如何完美卸载VS2015(2023年5月份实测有效)
使用控制面板卸载VS2015,出现正在配置您的系统,这可能需要一些时间,然后就出现卡住半个小时第二行的条都没有动的问题,这里提供vs2015以及以前版本的卸载方式 问题产生原因:他需要下载一些东西,然后由于你懂的网络原因…...

JavaScript如何声明和定义函数
JavaScript是一门非常有趣的编程语言,它可以让我们创建各种各样的函数来解决各种各样的问题。在JavaScript中,函数的声明和定义非常重要,因为它们决定了函数的行为和执行过程。 首先,让我们来看看JavaScript中函数的声明。在Java…...

微信小程序 WebSocket 通信 —— 在线聊天
在Node栏目就讲到了Socket通信的内容,使用Node实现Socke通信,还使用两个流行的WebSocket 库,ws 和 socket.io,在小程序中的WebSocket接口和HTML5的WebSocket基本相同,可以实现浏览器与服务器之间的全双工通信。那么本篇…...
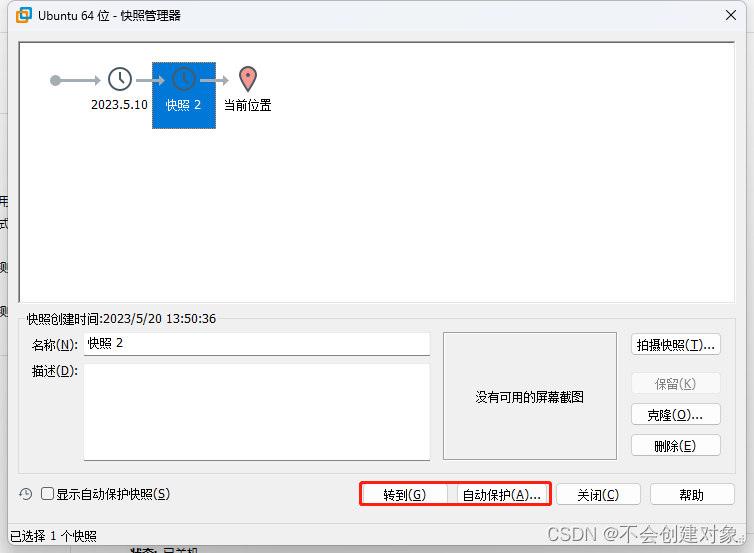
VMware快照:简化虚拟化环境管理与数据保护
引言: 在虚拟化环境中,数据保护和灵活性是至关重要的。VMware快照作为一项强大的功能,为虚拟机管理者提供了便利和安全性。本文将介绍VMware快照的使用,以及它为用户带来的几个关键优势。 VMware快照是一项重要的功能,…...
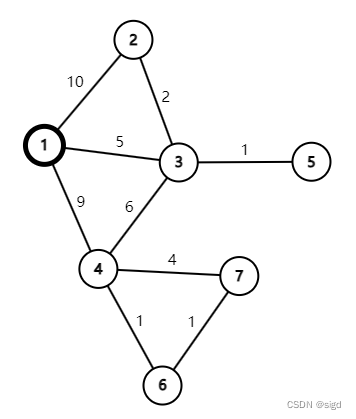
图的最短路径
最短路径算法对图结构没有特殊要求,不要求连通图,且有向图无向图均可。 最短路径算法目标是求得从某顶点出发,沿图的边到达另一顶点所经过的路径中,各边上权值之和最小的一条路径。解决最短路的问题有以下算法:Dijkst…...

RHCE----Shell变量和引用
1.变量的类型及含义 变量类型: 1、自定义变量: 在当前的shell命令行界面设置的变量是局部变量 例子: num1 namezhangsan 2、环境变量全局变量,通过export 导出后的局部变量是全局变量 、bash的初始化文件:/etc/profile:存放一些全局变量…...
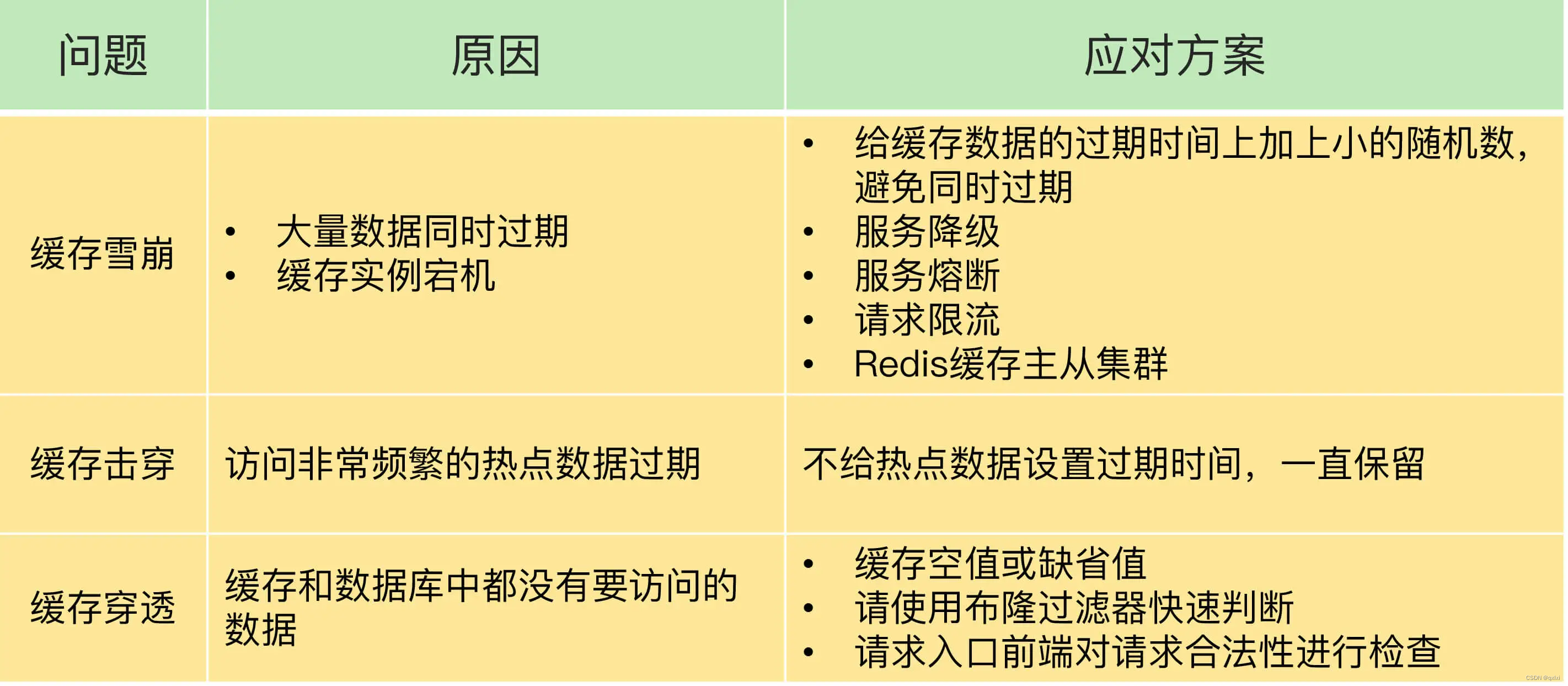
【Redis】聊一下缓存雪崩、击穿、穿透、预热
缓存的引入带来了数据读取性能的提升,但是因此也引入新的问题,一个是数据双写一致性,另一个就是雪崩、击穿、穿透,那么如何解决这些问题,我们来说下对应的问题和解决方案 雪崩 缓存雪崩:同一时间内大量请…...

全景描绘云原生技术图谱,首个《云原生应用引擎技术发展白皮书》发布
5月12日,由神州数码主办、北京经开区国家信创园、中关村云计算产业联盟协办的2023通明湖论坛-云原生分论坛在京召开。论坛期间,神州数码联合北京通明湖信息技术应用创新中心、中国信通院和通明智云正式发布了《云原生应用引擎技术发展白皮书》࿰…...
【Python共享文件】——Python快速搭建HTTP web服务实现文件共享并公网远程访问
文章目录 1. 前言2. 视频教程3. 本地文件服务器搭建3.1 python的安装和设置3.2 cpolar的安装和注册 4. 本地文件服务器的发布4.1 Cpolar云端设置4.2 Cpolar本地设置 5. 公网访问测试6. 结语 1. 前言 数据共享作为和连接作为互联网的基础应用,不仅在商业和办公场景有…...

Mysql数据库分库分表
为什么使用分库分表? 传统的将数据集中存储至单一数据节点的解决方案,在性能、可用性和运维成本这三方面已经难于满足互联网的海量数据场景。 1)性能 从性能方面来说,由于关系型数据库大多采用 B 树类型的索引,在数…...
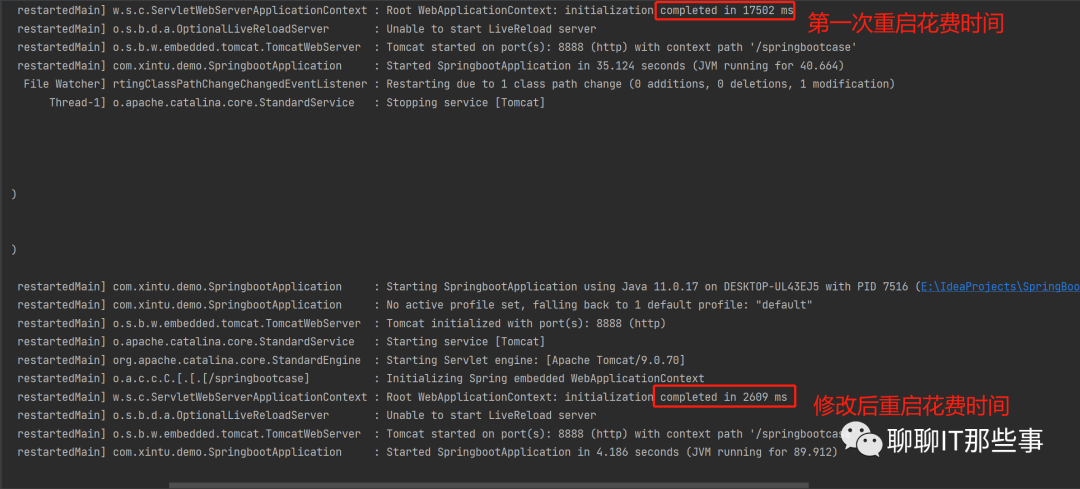
SpringBoot热部署插件原理分析及实战演练
目录 1、关于热部署(Hot Deploy)产生的背景 1)热部署出现前 2)热部署出现后 2、spring-boot-devtools插件原理 1)解决变更文件自动加载到JVM中 2)spring-boot-devtools重启速度比手动重启快 3、关于…...

【C++ 入坑指南】(10)函数
文章目录 简介定义实例函数的分文件编写 简介 函数是一组一起执行一个任务的语句。每个 C 程序都至少有一个函数,即主函数 main() ,所有简单的程序都可以定义其他额外的函数。 您可以把代码划分到不同的函数中。如何划分代码到不同的函数中是由您来决定…...
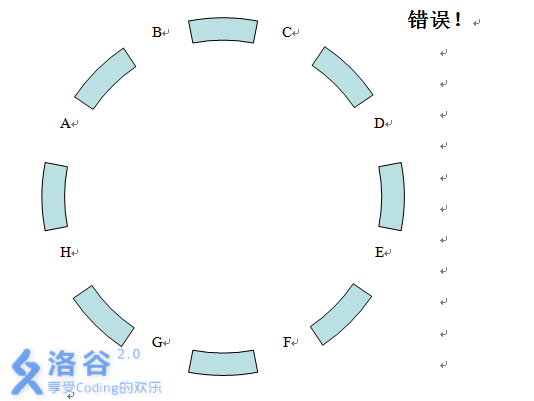
P2233 [HNOI2002]公交车路线
题目描述 在长沙城新建的环城公路上一共有 8 个公交站,分别为 A、B、C、D、E、F、G、H。公共汽车只能够在相邻的两个公交站之间运行,因此你从某一个公交站到另外一个公交站往往要换几次车,例如从公交站 A 到公交站 D,你就至少需要…...
网络编程)
java入门-W11(K168-K182)网络编程
1. 网络编程入门 1.1 网络编程概述 计算机网络 是指将地理位置不同的具有独立功能的多台计算机及其外部设备,通过通信线路连接起来,在网络操作系统,网络管理软件及网络通信协议的管理和协调下,实现资源共享和信息传递的计算机系统…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...
