图的最短路径
最短路径算法对图结构没有特殊要求,不要求连通图,且有向图无向图均可。
最短路径算法目标是求得从某顶点出发,沿图的边到达另一顶点所经过的路径中,各边上权值之和最小的一条路径。解决最短路的问题有以下算法:Dijkstra算法,Floyd算法和SPFA算法等。其中SPFA算法可以处理边权值为负数图结构。而最为好用的是使用堆优化的Dijstra算法。

(一)Dijkstra算法
算法采用动态规划的思想,通过对图结构的递推,得到从点X出发,到其他所有结点的最短路径(不能处理边权为负值情况)。以下图为例,求结点1出发,到其余各结点最短路径。
(1)先找到从1出发的邻接点有(2,3,4),最短的边是(1,3,长度5),此时可以断言结点1到结点3最短路径是5。证明也很容易,因为其他路径必须先经过(1,2,长度10)或者(1,4,长度9)那么其长度必然大于5。
(2)从3出发找寻到其他结点更短的路径,可以发现
5+(3,2,长度2)要比原来的(1,2,长度10)更小,进行数据的更新;
5+(3,5,长度6)就不如原有的(1,4,长度9),不作更新操作;
5+(3,5,长度1)要比原来的(1,5,长度无穷大)更小,进行数据的更新。
更新全部之后选出最小的路径,此时为(1,3,2)长度7,此路径为结点1到结点2的最短路径。然后从结点2出发继续找寻到其他结点更短的路径。
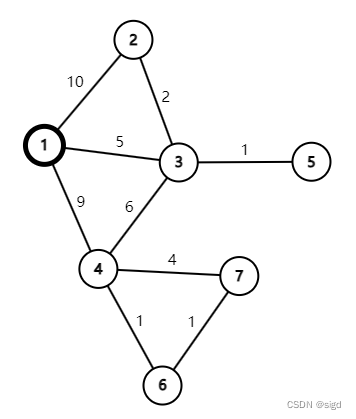
算法实现细节:(1)用v数组标记已经求出最短路径的结点;(2)用d数组记录最短路径长度,通过迭代方式更新d数组,找到当前最短路径结点。
邻接表存储的算法实现。
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
int n,m,v[105],d[105];
struct node
{int adj,val;
};
vector<node>e[105];
int getMin()
{int mini=0,i;for(i=1;i<=n;i++)if(v[i]==0&&d[i]<d[mini])mini=i;return mini;
}
void djstra(int s)
{int i,j;memset(d,127/3,sizeof(d));/**< 初始化d数组 */d[s]=0;/**< s为起点 */for(i=1; i<=n; i++){int temp=getMin();v[temp]=1;for(j=0; j<e[temp].size(); j++) /**< e[1] 存的是2 4 5,e[1][j] */{int x=e[temp][j].adj,z=e[temp][j].val;if(v[x]==0&&d[x]>d[temp]+z)d[x]=d[temp]+z;}}
}
int main()
{ios::sync_with_stdio(0),cin.tie(0);int i,j,x,y,z,ans=0;cin>>n>>m;for(i=1; i<=m; i++){cin>>x>>y>>z;e[x].push_back({y,z});e[y].push_back({x,z});}djstra(1);if(d[n]<1e8)cout<<d[n];elsecout<<-1;return 0;
}
邻接表用堆优化的算法
#include <iostream>
#include<cstring>
#include <queue>
#include<vector>
typedef long long ll;
using namespace std;
int n,m,v[105],d[105];
struct node
{int adj,val;bool operator<(const node B)const/**< 重载操作符,用于优先队列排序 */{return val>B.val;}
};
vector<node>e[105];
priority_queue<node>pq;
int getMin()/**< 用堆之后查找复杂度降为log级别 */
{while(pq.size()&&v[pq.top().adj])/**< 存在堆顶元素已经访问的情况 */pq.pop();int v=pq.top().adj;pq.pop();return v;
}
void djstra(int s)
{int i,j;memset(d,127/3,sizeof(d));/**< 初始化d数组 */d[s]=0;/**< s为起点 */for(i=1; i<=n; i++)/**< 初始化优先队列,放入结点i和对应的d[i],这里只是借用node类型,这两个值可不是邻接点和权值(正常来说需要再定义一个结构体类型) */pq.push({i,d[i]});for(i=1; i<=n; i++){int temp=getMin();v[temp]=1;for(j=0; j<e[temp].size(); j++) /**< e[1] 存的是2 4 5,e[1][j] */{int x=e[temp][j].adj,z=e[temp][j].val;if(v[x]==0&&d[x]>d[temp]+z)d[x]=d[temp]+z,pq.push({x,d[x]});}}
}
int main()
{ios::sync_with_stdio(0),cin.tie(0);int i,j,x,y,z,ans=0;cin>>n>>m;for(i=1; i<=m; i++){cin>>x>>y>>z;e[x].push_back({y,z});e[y].push_back({x,z});}djstra(1);if(d[n]<1e8)cout<<d[n];elsecout<<-1;return 0;
}
(二)Floyd算法
必须使用邻接矩阵存储结构。基于动态规划思想,通过n个点的拉伸得到任意两点最短路径。检查每一个结点k,试探能否通过k为中间结点减少结点i和j的最短路径长度。Floyd算法时间复杂度较高O(n3),但是能用于求任意两点最短路径。算法简单,只适用于结点数较少的情况。
#include <iostream>
#include <cstring>
typedef long long ll;
using namespace std;
int n,m,a[105][105];
int main()
{ios::sync_with_stdio(0),cin.tie(0);int i,j,k,x,y,z;cin>>n>>m;memset(a,127/3,sizeof(a));for(i=1;i<=m;i++){cin>>x>>y>>z;/**< 必须无向图 */a[x][y]=a[y][x]=z;}for(k=1;k<=n;k++){for(i=1;i<=n;i++){for(j=1;j<=n;j++){if(a[i][j]>a[i][k]+a[k][j])/**< 检查以k为中间点,是否能减少i和j的路径长度 */a[i][j]=a[i][k]+a[k][j];}}}if(a[1][n]>9999999)cout<<-1;elsecout<<a[1][n];return 0;
}
(三)SPFA算法
SPFA算法写起来和BFS算法几乎一模一样,也被称为队列优化算法,通常用于求含负权边的单源最短路径,以及判负权环。其处理过程和迪杰斯特拉区别在于,迪杰斯特拉算法需要找到最小的那个结点,而SPFA不管那些,只要一个结点的当前路径长度低于之前已有的值,那么就送入队列,因为新的路径长度可能刷新其他结点的最短路径长度。
#include <iostream>
#include <string.h>
#include<vector>
#include<queue>
typedef long long ll;
using namespace std;
int n,m,v[100005],d[100005];/**< V表示结点是否在队列中 */
vector< pair<int,int> > e[100005];
void spfa(int x)
{int i,temp;d[x]=0;queue<int>q;q.push(x);/**< 起点入队 */while(!q.empty()){temp=q.front();/**< temp出队结点,如果一个结点会反复入队出队超过n次,那么有负环存在 */q.pop();v[temp]=0;/**< 修改标志,未来可能会再次入队 */for(i=0;i<e[temp].size();i++){int y=e[temp][i].first,z=e[temp][i].second;if(d[y]>d[temp]+z) /**< y结点的路径长度变短 */{d[y]=d[temp]+z;if(v[y]==0)/**< 如果y结点此时不在队列中,加入队列中 */{q.push(y);v[y]=1;/**< 标记一下,假如在y出来之前又一次d[y]>d[temp]+z,那么也不用重复入队 */}}}}
}
int main()
{ios::sync_with_stdio(0),cin.tie(0);int i,j,x,y,z,s;cin>>n>>m;for(i=1;i<=m;i++){cin>>x>>y>>z;if(x==y)continue;e[x].push_back({y,z});e[y].push_back({x,z});}memset(d,127,sizeof(d));spfa(1);cout<<(d[n]>9999999?-1:d[n]);return 0;
}
相关文章:

图的最短路径
最短路径算法对图结构没有特殊要求,不要求连通图,且有向图无向图均可。 最短路径算法目标是求得从某顶点出发,沿图的边到达另一顶点所经过的路径中,各边上权值之和最小的一条路径。解决最短路的问题有以下算法:Dijkst…...

RHCE----Shell变量和引用
1.变量的类型及含义 变量类型: 1、自定义变量: 在当前的shell命令行界面设置的变量是局部变量 例子: num1 namezhangsan 2、环境变量全局变量,通过export 导出后的局部变量是全局变量 、bash的初始化文件:/etc/profile:存放一些全局变量…...
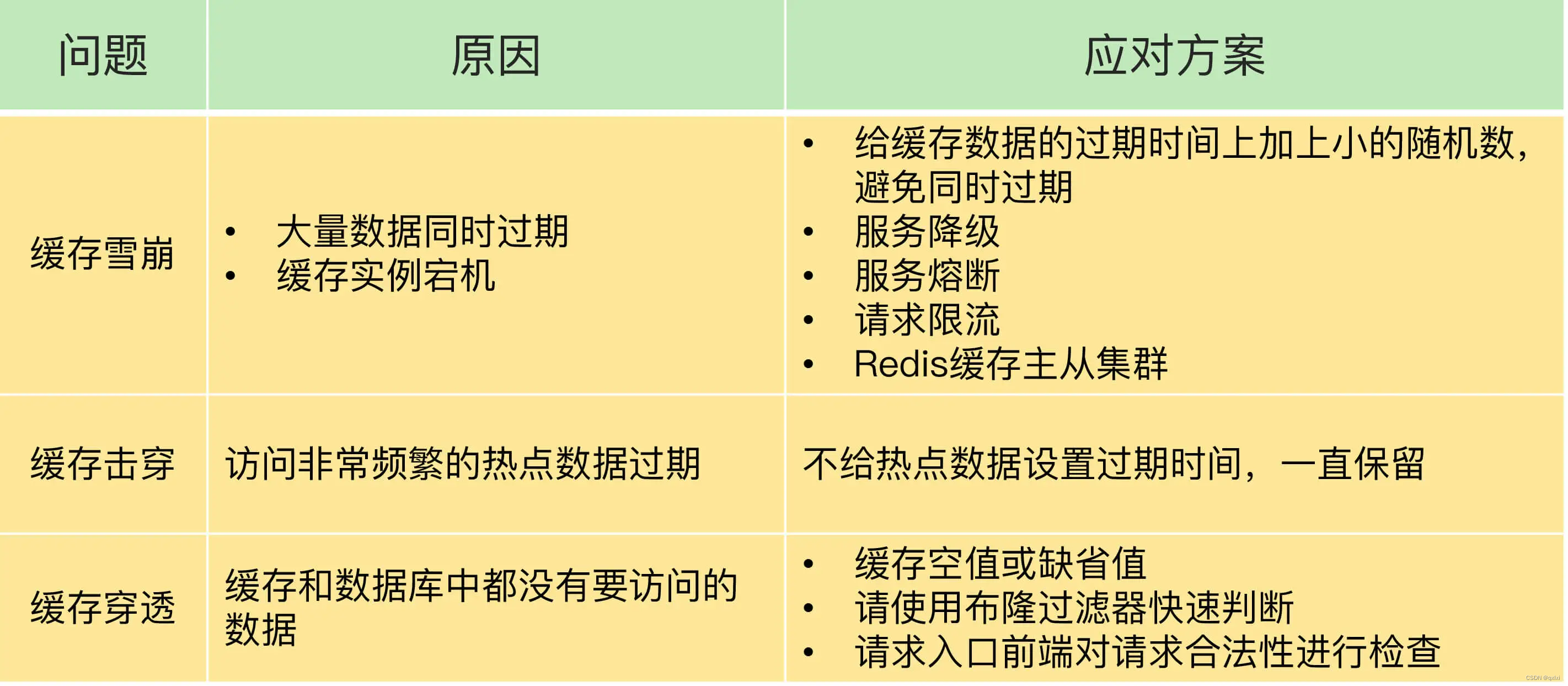
【Redis】聊一下缓存雪崩、击穿、穿透、预热
缓存的引入带来了数据读取性能的提升,但是因此也引入新的问题,一个是数据双写一致性,另一个就是雪崩、击穿、穿透,那么如何解决这些问题,我们来说下对应的问题和解决方案 雪崩 缓存雪崩:同一时间内大量请…...

全景描绘云原生技术图谱,首个《云原生应用引擎技术发展白皮书》发布
5月12日,由神州数码主办、北京经开区国家信创园、中关村云计算产业联盟协办的2023通明湖论坛-云原生分论坛在京召开。论坛期间,神州数码联合北京通明湖信息技术应用创新中心、中国信通院和通明智云正式发布了《云原生应用引擎技术发展白皮书》࿰…...
【Python共享文件】——Python快速搭建HTTP web服务实现文件共享并公网远程访问
文章目录 1. 前言2. 视频教程3. 本地文件服务器搭建3.1 python的安装和设置3.2 cpolar的安装和注册 4. 本地文件服务器的发布4.1 Cpolar云端设置4.2 Cpolar本地设置 5. 公网访问测试6. 结语 1. 前言 数据共享作为和连接作为互联网的基础应用,不仅在商业和办公场景有…...

Mysql数据库分库分表
为什么使用分库分表? 传统的将数据集中存储至单一数据节点的解决方案,在性能、可用性和运维成本这三方面已经难于满足互联网的海量数据场景。 1)性能 从性能方面来说,由于关系型数据库大多采用 B 树类型的索引,在数…...
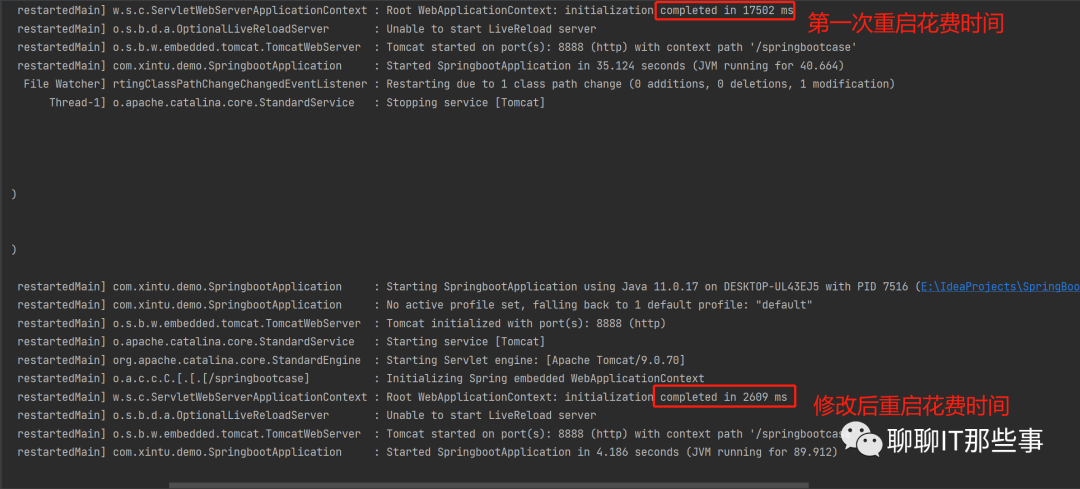
SpringBoot热部署插件原理分析及实战演练
目录 1、关于热部署(Hot Deploy)产生的背景 1)热部署出现前 2)热部署出现后 2、spring-boot-devtools插件原理 1)解决变更文件自动加载到JVM中 2)spring-boot-devtools重启速度比手动重启快 3、关于…...

【C++ 入坑指南】(10)函数
文章目录 简介定义实例函数的分文件编写 简介 函数是一组一起执行一个任务的语句。每个 C 程序都至少有一个函数,即主函数 main() ,所有简单的程序都可以定义其他额外的函数。 您可以把代码划分到不同的函数中。如何划分代码到不同的函数中是由您来决定…...
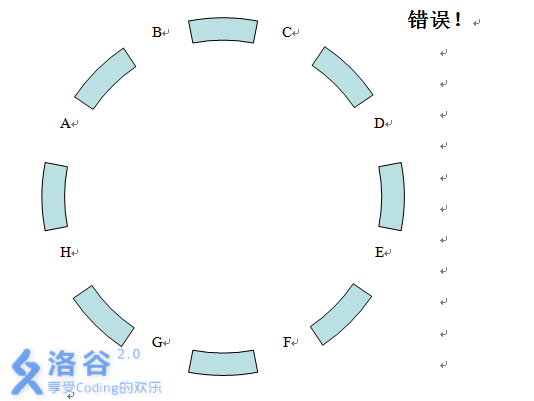
P2233 [HNOI2002]公交车路线
题目描述 在长沙城新建的环城公路上一共有 8 个公交站,分别为 A、B、C、D、E、F、G、H。公共汽车只能够在相邻的两个公交站之间运行,因此你从某一个公交站到另外一个公交站往往要换几次车,例如从公交站 A 到公交站 D,你就至少需要…...
网络编程)
java入门-W11(K168-K182)网络编程
1. 网络编程入门 1.1 网络编程概述 计算机网络 是指将地理位置不同的具有独立功能的多台计算机及其外部设备,通过通信线路连接起来,在网络操作系统,网络管理软件及网络通信协议的管理和协调下,实现资源共享和信息传递的计算机系统…...

距离6月18日DAMA-CDGA/CDGP认证考试还有31天,报名从速
6月18日DAMA-CDGA/CDGP数据治理认证考试开放报名中! 考试开放地区:北京、上海、广州、深圳、长沙、呼和浩特、杭州、南京、济南、成都、西安。其他地区凑人数中… DAMA-CDGA/CDGP数据治理认证班进行中,报名从速! DAMA认证为数据管…...

PO、VO、DAO、BO、DTO、POJO区分
一 分层领域模型规约: DO(Data Object):此对象与数据库表结构一一对应,通过 DAO 层向上传输数据源对象。DTO(Data Transfer Object):数据传输对象,Service 或 Manager 向外传输的对象。BO(Business Object):业务对象,由 Service 层输出的封装…...
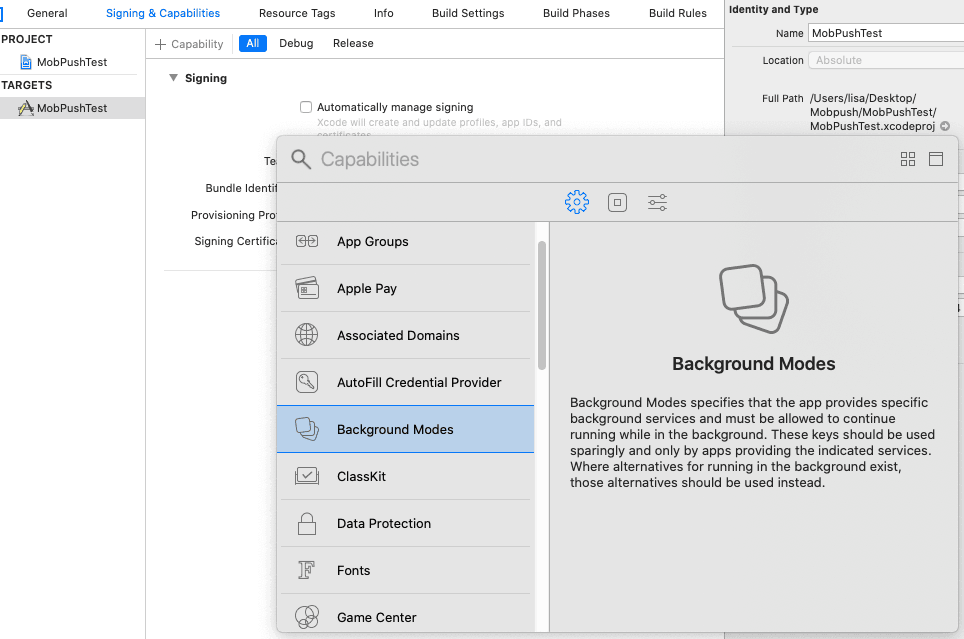
MobPush Flutter平台插件
集成准备 注册账号 使用PushSDK之前,需要先在MobTech官网注册开发者账号,并获取MobTech提供的AppKey和AppSecret,详情可以点击查看注册流程 MobPush后台配置 注册MobTech账号后,需要在MobTech后台进行相关信息的配置ÿ…...

机器学习面试题库:K-means
一、简述K-means算法的原理及工作流程? 原理: K-means是一个无监督的聚类算法。它的主要目的是对同一组数据对象进行分类。其原理是基于样本间的相似性来聚类分析的,即将所有样本分为K个簇,使得同一个簇间中样本相似性最高&#…...

Linux:文本三剑客之awk
Linux:文本三剑客之awk 一、awk编辑器1.1 awk概述1.2 awk工作原理1.3 awk与sed的区别 二、awk的应用2.1 命令格式2.2 awk常见的内建变量(可直接用) 三、awk使用3.1 按行输出文本3.2 按字段输出文本3.3 通过管道、双引号调用 Shell 命令 一、a…...
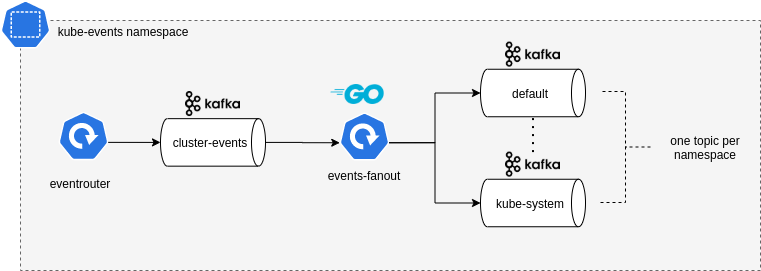
如何借助Kafka持久化存储K8S事件数据?
大家应该对 Kubernetes Events 并不陌生,特别是当你使用 kubectl describe 命令或 Event API 资源来了解集群中的故障时。 $ kubectl get events15m Warning FailedCreate …...
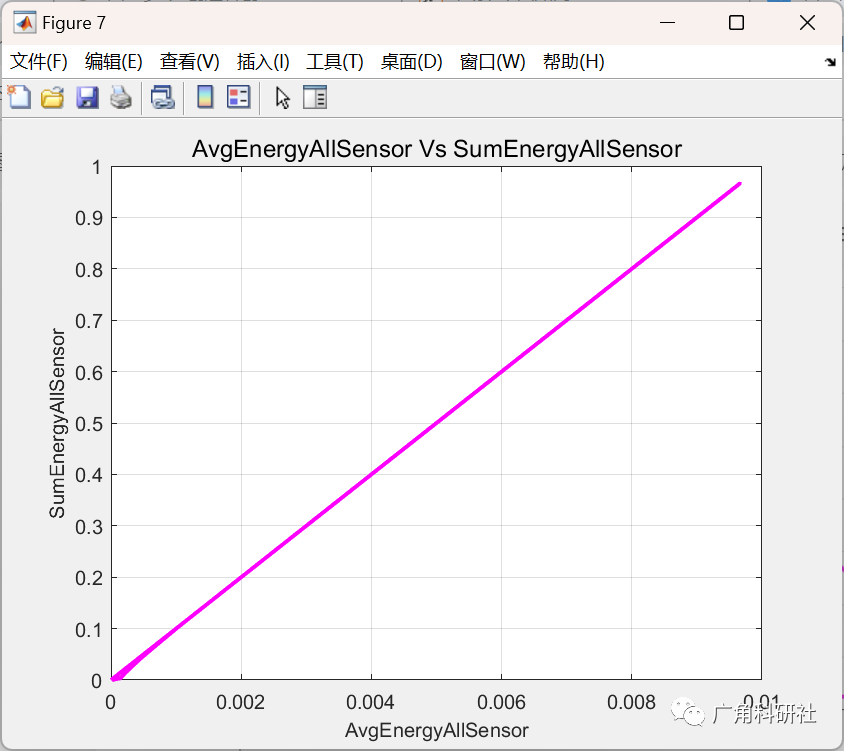
一种基于非均匀分簇和建立簇间路由的算法的无线传感器网络路由协议(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨💻4 Matlab代码 💥1 概述 本文准备了一种路由方法,该方法使传感器通过有效地使用能量将数据从发送方加载到接收器,因为它在 LEAC…...
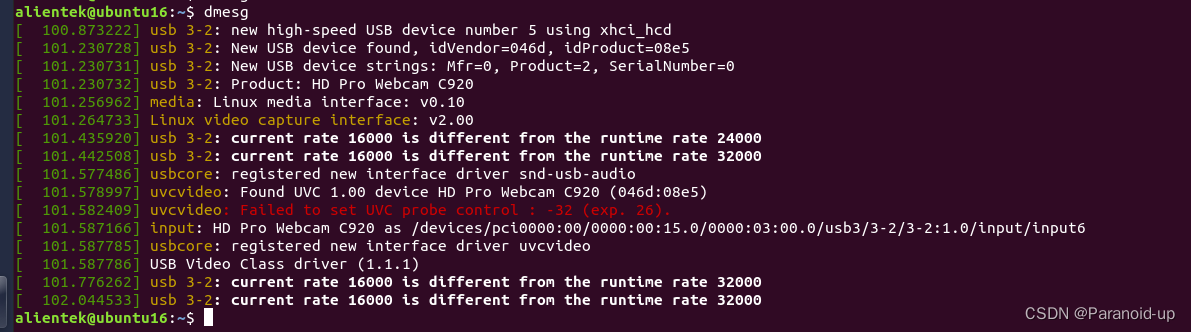
usb摄像头驱动打印信息
usb摄像头驱动打印信息 文章目录 usb摄像头驱动打印信息 在ubuntu中接入罗技c920摄像头打印的信息如下: [ 100.873222] usb 3-2: new high-speed USB device number 5 using xhci_hcd [ 101.230728] usb 3-2: New USB device found, idVendor046d, idProduct08e5 …...

银行半结构化和无领导群面注意事项
银行可以同时报考多家,因此部分同学也积累了不少宝贵的面试“失败”经验。今天小编就来给大家说说半结构化和无领导群面的注意事项,从如信银行考试中心了解到的整理如下: 一、半结构化面试注意事项: 半结构化面试更侧重于了解考生…...

今天公司来了个拿 30K 出来的测试,算是见识到了基础的天花板
今天上班开早会就是新人见面仪式,听说来了个很厉害的大佬,年纪还不大,是上家公司离职过来的,薪资已经达到中高等水平,很多人都好奇不已,能拿到这个薪资应该人不简单,果然,自我介绍的…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...
