机器学习面试题库:K-means
一、简述K-means算法的原理及工作流程?
原理:
K-means是一个无监督的聚类算法。它的主要目的是对同一组数据对象进行分类。其原理是基于样本间的相似性来聚类分析的,即将所有样本分为K个簇,使得同一个簇间中样本相似性最高,不同簇间样本相似性最低。
工作流程:
1.初始化:随机选择K个样本作为初始化簇心
2.分配:对于每个样本,计算其到每个簇心的距离,并将分配到距离最短的簇中
3.重新计算簇心:重新计算每个簇的簇心
4.重复步骤2和步骤3,直至簇心不在发生变化,或者达到预定的聚类次数。
二、K-means聚类中的K如何取?
确定K的值是K-means聚类算法中最重要的问题之一,一般可以采用以下两种方法来确定K的合适取值:
-
手肘法:通过计算不同K值下聚类结果的SSE(误差平方和)或SSB(组间平方和)值,观察这些指标与K值的关系,找到SSE或SSB下降速度趋于平稳的K值,即所谓的“肘部”位置,作为合适的聚类数。
-
轮廓系数法:通过计算不同K值下聚类结果中每个样本的轮廓系数,综合考虑聚类结果的紧密度和分离度,找到轮廓系数达到最大值时对应的K值,作为最佳聚类数。
需要注意的是,以上方法只是参考,无法保证一定能够得到最优的K值,实际应用中可能需要结合业务需求和实际场景综合考虑。
三、常见的距离度量方式有那些?
常见的距离度量方式有以下几种:
-
欧几里得距离(Euclidean Distance):是指在m维空间中两个点之间的真实距离,即勾股定理。在实际应用中,欧几里得距离被广泛应用于K-means算法中。
-
曼哈顿距离(Manhattan Distance):是指在m维空间中两点之间的城市街区距离,即横、纵坐标绝对值的和。
-
闵可夫斯基距离(Minkowski Distance):是指在m维空间中两点之间的距离,在欧几里得距离和曼哈顿距离的基础上进行推广,公式为$d=(\sum_{i=1}^m|X_i-Y_i|^p)^{\frac{1}{p}}$,其中p为距离度量的阶数,当p=1和2时,闵可夫斯基距离分别对应曼哈顿距离和欧几里得距离。
-
切比雪夫距离(Chebyshev Distance):是指在二维空间中两点之间的切比雪夫距离,即两点横、纵坐标差的绝对值的最大值。
-
余弦相似度(Cosine Similarity):是指用向量空间中两个向量夹角的余弦值作为衡量它们之间的相似性,适用于文本分类、信息检索等领域。
四、马氏距离和欧式距离的区别是什么?
欧式距离和马氏距离都是用来度量样本之间的距离,二者的区别如下:
-
度量方式不同:欧式距离是指欧几里得距离,即二维空间中两点之间的真实距离;而马氏距离则是在样本协方差矩阵的基础上进行计算的,能够考虑不同特征之间的相关性和方差。
-
应用范围不同:欧式距离适用于绝大多数情况下,如图像分类、文本分类、聚类等;而马氏距离则更适合于处理高维度、相关数据。
-
距离结果的表达方式不同:欧式距离的结果是一个标量,反映两个样本之间的距离;而马氏距离的结果是一个矩阵,反映样本之间的相关性。
总的来说,欧式距离是一种通用的度量距离的方式,在绝大多数情况下都能够使用;而马氏距离则更适合于处理含有相关性变量的高维数据。
五、K-means聚类对空簇如何处理?
在K-means聚类算法中,空簇是指在某一轮迭代后没有样本点被划分到该簇中的情况。对于空簇,一般可以采用以下两种方法进行处理:
-
随机分配法:可以将空簇内的质心随机分配给剩余的簇。这样可以保证建立的新簇数不变,不影响后续的聚类计算。
-
剔除法:可以将空簇直接剔除,同时将聚类数目减1,然后重新进行聚类计算。由于空簇的存在可能会导致分类结果不够准确,因此剔除空簇也是一个常见的处理方法。
需要注意的是,处理空簇的方法应该根据具体问题而定,考虑到数据的性质和应用场景选择一个合适的方法。在实际应用中,可以尝试多种方法并进行比较,以得到最好的聚类结果。
六、为什么K-means聚类会容易收到异常值的影响
K-means聚类算法的本质是在寻找每个簇的中心点,进而对样本点进行划分。这就意味着它容易受到异常值的影响。由于异常值偏离了大多数点的分布,它们会改变每个簇的中心位置,并且在迭代过程中会影响质心的计算。如果异常值的数量很多,那么K-means可能会出现明显的错误,如不合理的簇划分、聚类数目偏少等。
为了减少异常值的影响,我们可以采用以下两种方法:
-
离群值检测和剔除:可以使用一些离群值检测算法,如Z-score或箱线图等方法,来识别和剔除离群值,以减少异常值对聚类结果的影响。
-
选择合适的距离度量方式:如曼哈顿距离等距离度量方式提供了对异常值的一定鲁棒性,可以减轻异常值的影响。
需要注意的是,剔除异常值可能会导致数据信息丢失,因此需要根据具体问题和应用场景进行相应的权衡和考虑。
七、如何对K-means聚类的效果进行评估?
K-means聚类是一种无监督学习算法,通常无法事先确定簇的数量或分类结果的正确性。因此对于K-means算法的评估主要基于内部指标和外部指标两种方法。
-
内部指标:主要是针对聚类结果本身的评估指标,比如样本间距离、簇内距离、簇间距离、簇内平均距离、轮廓系数等。这些指标可以帮助判断聚类结果的紧密性和一致性,从而确定最佳聚类数量,并对不同的聚类结果进行比较。
-
外部指标:主要是通过与已知分类或真实标签进行对比,评估聚类结果的正确性和准确性。比如精确率、召回率、F1值等指标。这些指标通常需要已知样本的真实标签或分类信息,因此只适用于那些有人工标注或已知分类的数据集。
同时,需要注意的是,K-means算法的评估指标存在一定的局限性,如聚类的结果依赖于初始质心的选择,存在可能陷入局部最优解的问题等。因此,在使用K-means算法时,需要注意选择合适的评估指标,并结合实际问题和经验进行综合判断和分析。
八、简述K-means聚类的优缺点?
K-means聚类是一种常见的无监督学习算法,通过将数据集中的样本划分到不同的簇中,从而实现对数据集的分析和分类。它的优点和缺点如下:
优点:
-
简单易用:K-means算法是一种简单易用的聚类方法,不需要任何先验知识和标记,可以自动发现数据的内在规律。
-
速度快:K-means算法计算量小,在数据量较大时也能以较快的速度实现分类。
-
可扩展性好:K-means算法的计算过程容易分布式实现,并且可以方便地应用于大规模数据集的聚类任务。
-
结果可解释性好:K-means算法将每个数据点分配到最近的质心中,所以簇的分割结果易于理解。同时,可以通过可视化手段直观地展示聚类效果。
缺点:
-
对初始质心敏感:随机化的初始质心选择方法会导致K-means算法对于不同的初始值产生不同的输出结果。
-
容易收敛于局部最优:由于在初始质心的选择和簇的合并过程中,会陷入局部最优解,从而可能得到不理想的聚类结果。
-
聚类数量需先验确定:在应用K-means算法时,需要手动确定合适的簇的数量K,且簇的数量可能很难事先估计。
-
对于非球形的簇效果欠佳:K-means算法假设每个簇是一个球形分布,对于非球形或不规则簇的聚类效果不佳。
需要注意的是,K-means算法的优缺点需要在具体应用场景中综合考虑。对于规模较小、簇形态较简单、具体规律明显的数据集,K-means算法的效果良好;对于复杂、高维数据集,可能需要考虑其他更加复杂的聚类算法。
九、K-means聚类中,如何规避不同质心选取对聚类结果的影响?
K-means聚类算法是一种迭代型的聚类算法,其中选择质心是一项重要的操作。不同的质心选择会导致不同的聚类结果。为了避免不同质心选择对聚类结果的影响,可以考虑以下几种方法:
-
多次运行聚类:可以通过多次运行聚类算法,每次使用不同的质心初始化方法,然后选择最好的聚类结果。多次运行聚类可以有效降低质心选择对结果的影响,并增加聚类稳定性和准确性。
-
选择多个随机初始质心:一种简单的方法是通过同时选择多组随机初始质心,然后平均多个聚类结果来减小初始质心选择对聚类结果的影响。
-
选择合适的初始质心:除了使用随机初始质心的方法,还可以采用基于特征分析的方法,比如利用PCA(主成分分析)或TSNE(T分布邻域嵌入)等方法减少不同质心选取带来的影响。
需要注意的是,虽然质心选择是K-means聚类算法中一个重要的因素,但是对于大规模的数据集,通常可以通过多次迭代和加入合适的正则化方法等措施来减小初始质心对聚类结果的影响。因此,在实际的应用中,需要根据具体问题和数据集特点选择合适的处理方法。
十、K-means聚类和DBSCAN算法的对比?
K-means聚类和DBSCAN聚类算法都是经典的聚类算法,但它们的原理和应用场景有所不同。具体来说,它们的区别如下:
-
原理不同:K-means算法是基于质心的距离来实现聚类的,它寻找一组质心分别代表不同的簇,并以此划分数据集。而DBSCAN聚类算法是基于密度的距离来实现聚类的,通过不断扩展核心对象的直接密度可达区域,找出密度连接的点进行聚类。
-
适用场景不同:K-means算法适用于数据规模较大且数据的特征呈现出近似于球状分布的数据集。DBSCAN更适合于数据集中存在不同密度区域的情况,并且可以有效地发现任意形状的簇,对于噪声和异常值的处理也相对较好。
-
参数设置不同:K-means算法需要给定聚类的数量K,而DBSCAN算法不需要事先确定具体的聚类数目。
-
聚类效果不同:K-means算法的聚类效果可能会收到初始质心的选择影响,因此需要通过多次试验来选择最优质心。而DBSCAN算法的聚类效果的稳定性相对较好。
因此,对于数据分布近似于球形的数据集,且需要事先知道聚类数量的情况下,可以使用K-means聚类。而对于具有复杂数据分布,且聚类数量未知的数据集,则可以使用DBSCAN算法。当然,在实际应用中,还需要考虑数据量大小、数据维度、算法的计算效率等因素,选择最合适的算法。
相关文章:

机器学习面试题库:K-means
一、简述K-means算法的原理及工作流程? 原理: K-means是一个无监督的聚类算法。它的主要目的是对同一组数据对象进行分类。其原理是基于样本间的相似性来聚类分析的,即将所有样本分为K个簇,使得同一个簇间中样本相似性最高&#…...

Linux:文本三剑客之awk
Linux:文本三剑客之awk 一、awk编辑器1.1 awk概述1.2 awk工作原理1.3 awk与sed的区别 二、awk的应用2.1 命令格式2.2 awk常见的内建变量(可直接用) 三、awk使用3.1 按行输出文本3.2 按字段输出文本3.3 通过管道、双引号调用 Shell 命令 一、a…...
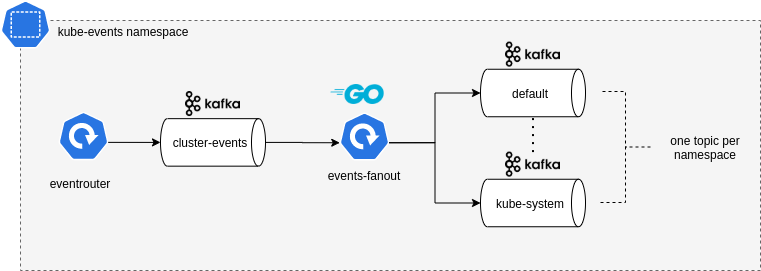
如何借助Kafka持久化存储K8S事件数据?
大家应该对 Kubernetes Events 并不陌生,特别是当你使用 kubectl describe 命令或 Event API 资源来了解集群中的故障时。 $ kubectl get events15m Warning FailedCreate …...
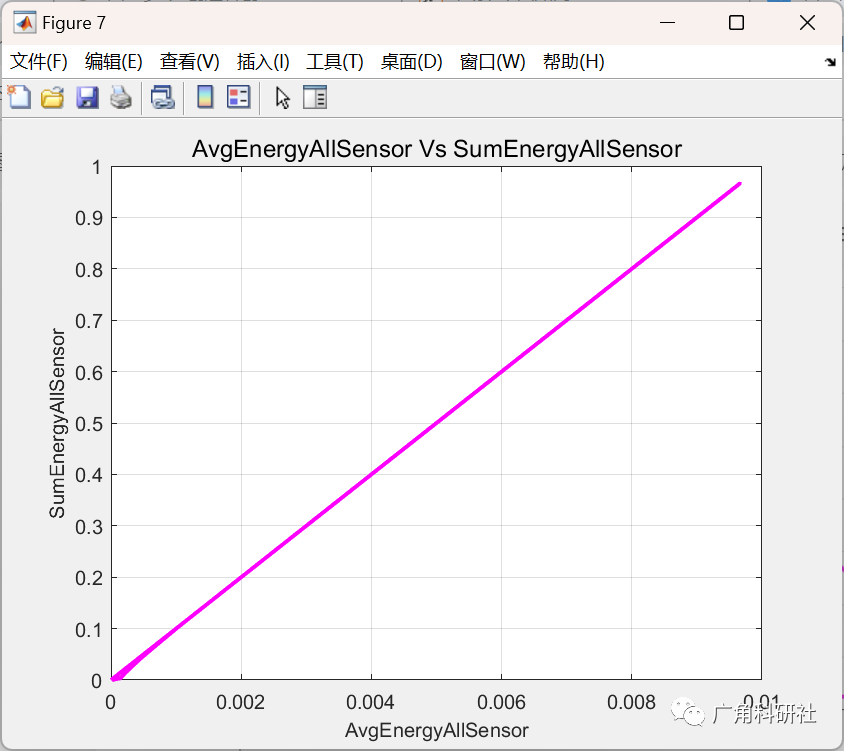
一种基于非均匀分簇和建立簇间路由的算法的无线传感器网络路由协议(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨💻4 Matlab代码 💥1 概述 本文准备了一种路由方法,该方法使传感器通过有效地使用能量将数据从发送方加载到接收器,因为它在 LEAC…...
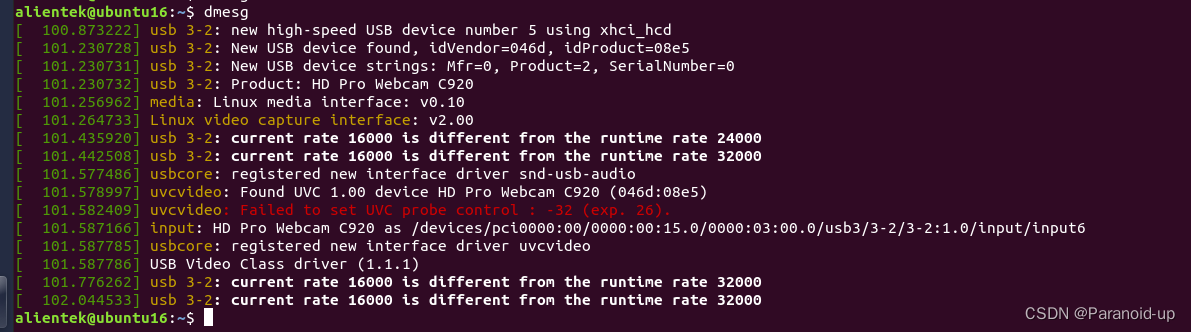
usb摄像头驱动打印信息
usb摄像头驱动打印信息 文章目录 usb摄像头驱动打印信息 在ubuntu中接入罗技c920摄像头打印的信息如下: [ 100.873222] usb 3-2: new high-speed USB device number 5 using xhci_hcd [ 101.230728] usb 3-2: New USB device found, idVendor046d, idProduct08e5 …...

银行半结构化和无领导群面注意事项
银行可以同时报考多家,因此部分同学也积累了不少宝贵的面试“失败”经验。今天小编就来给大家说说半结构化和无领导群面的注意事项,从如信银行考试中心了解到的整理如下: 一、半结构化面试注意事项: 半结构化面试更侧重于了解考生…...

今天公司来了个拿 30K 出来的测试,算是见识到了基础的天花板
今天上班开早会就是新人见面仪式,听说来了个很厉害的大佬,年纪还不大,是上家公司离职过来的,薪资已经达到中高等水平,很多人都好奇不已,能拿到这个薪资应该人不简单,果然,自我介绍的…...
SSM整合(单元测试、结果封装、异常处理)
文章目录 1,SSM整合1.1 流程分析1.2 整合配置步骤1:创建Maven的web项目步骤2:添加依赖步骤3:创建项目包结构步骤4:创建SpringConfig配置类步骤5:创建JdbcConfig配置类步骤6:创建MybatisConfig配置类步骤7:创建jdbc.properties步骤8:创建SpringMVC配置类步…...

C++ list
C list 📟作者主页:慢热的陕西人 🌴专栏链接:C 📣欢迎各位大佬👍点赞🔥关注🚓收藏,🍉留言 本博客主要内容介绍了C中list和相关接口的使用 Clist C listⅠ. li…...
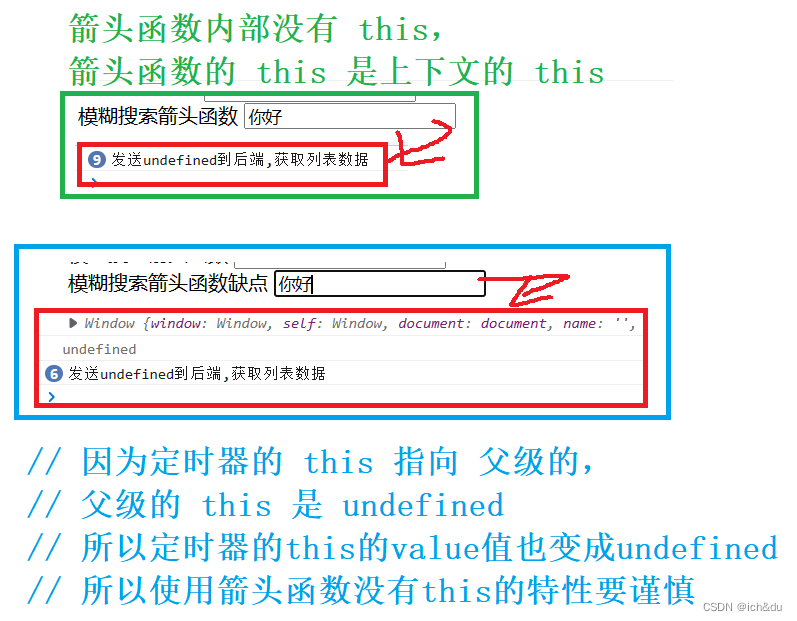
【JavaScript】ES6新特性(2)
5. 字符串扩展 5.1 includes函数 判断字符串中是否存在指定字符 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name&q…...
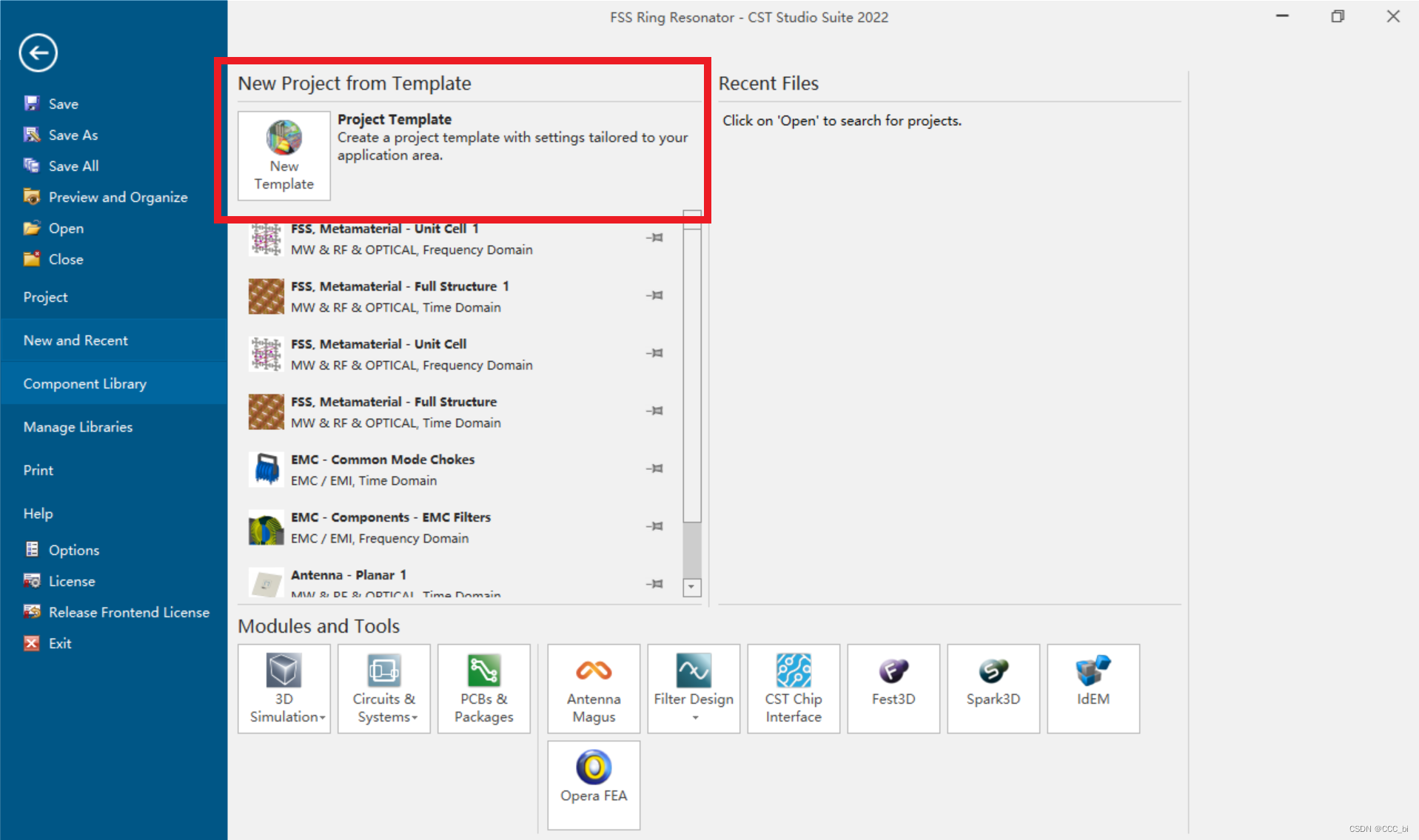
CST-FSS/周期谐振单元的仿真
引言 这几天要仿真超表面,上下求索CST有关相关内容的教程,视频倒是有不少,不过发现很多人忽略了官方帮助文档。本文以官方帮助文档为基础,写一个有关使用CST实现FSS/超表面这类周期结构的笔记。 官方帮助文档 CST有关FSS的内容使用了一个金属谐振圆环作为例子,这是由于…...
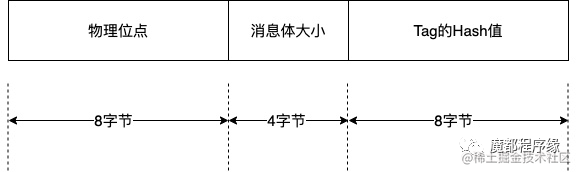
重新理解RocketMQ Commit Log存储协议
最近突然感觉:很多软件、硬件在设计上是有root reason的,不是by desgin如此,而是解决了那时、那个场景的那个需求。一旦了解后,就会感觉在和设计者对话,了解他们的思路,学习他们的方法,思维同屏…...
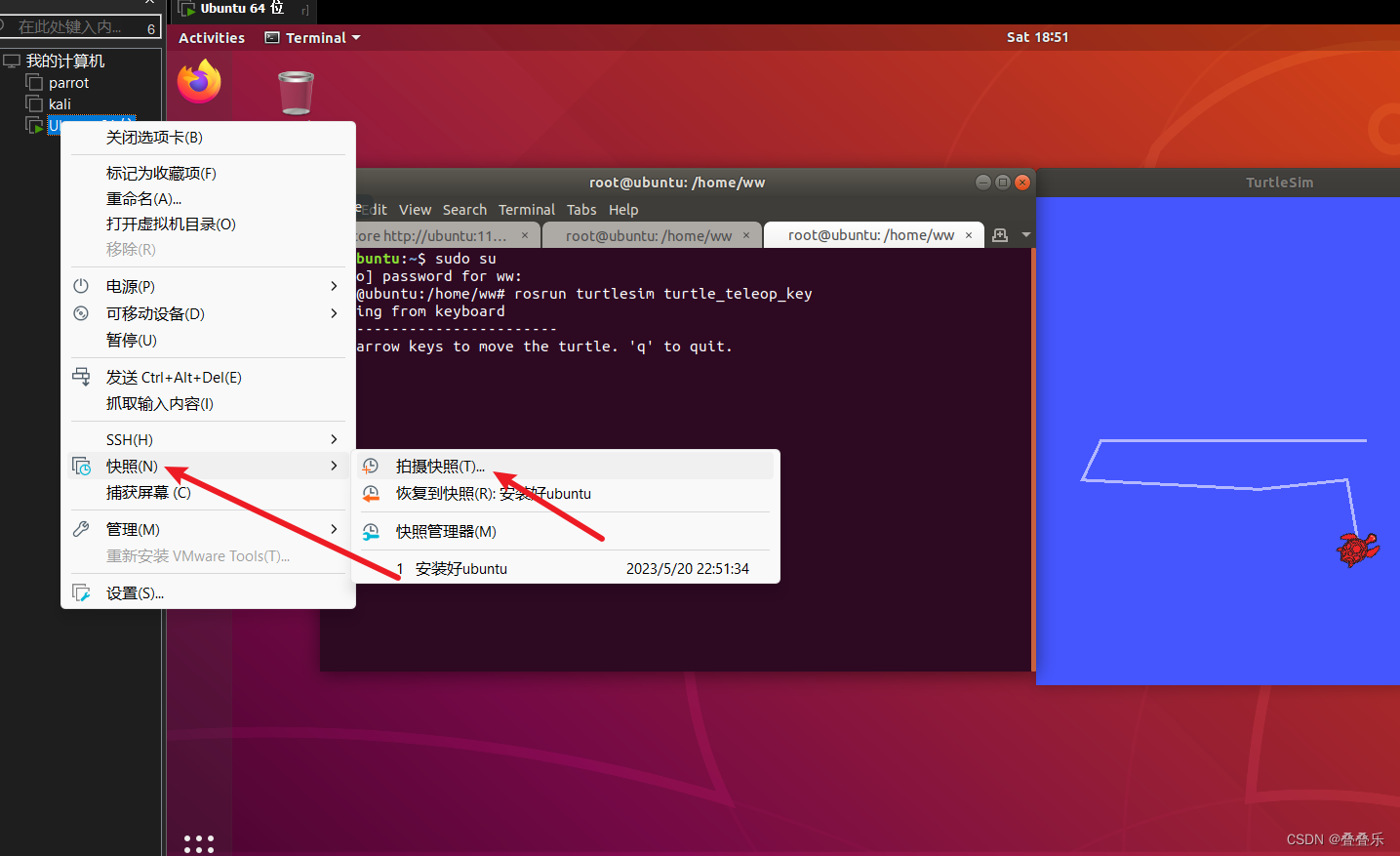
ROS 开发环境搭建(虚拟机版本)(一)
相关工具,以及镜像(以后有用) 链接:https://pan.baidu.com/s/1xgtp-XGFFNCACV_-0TJO2A 提取码:ar1w 1. 下载vm虚拟机(我选择的官方最新的vm虚拟机),安装好 2.安装百度网盘里面的…...

vue3做项目是需要注意的事项
Vue.js是一款非常优秀的前端开发框架,其第三代版本Vue3已经发布了。Vue3在性能、体验和功能等方面有了很大的提升,因此它成为了前端工程师们关注的焦点之一。在使用Vue3做项目时,有一些需要注意的事项,以下是对这些注意事项的介绍…...

docker日志轮转
cat /etc/docker/daemon.json { "log-driver": "json-file", "log-opts": { "max-size": "250m", "max-file": "3" } }...
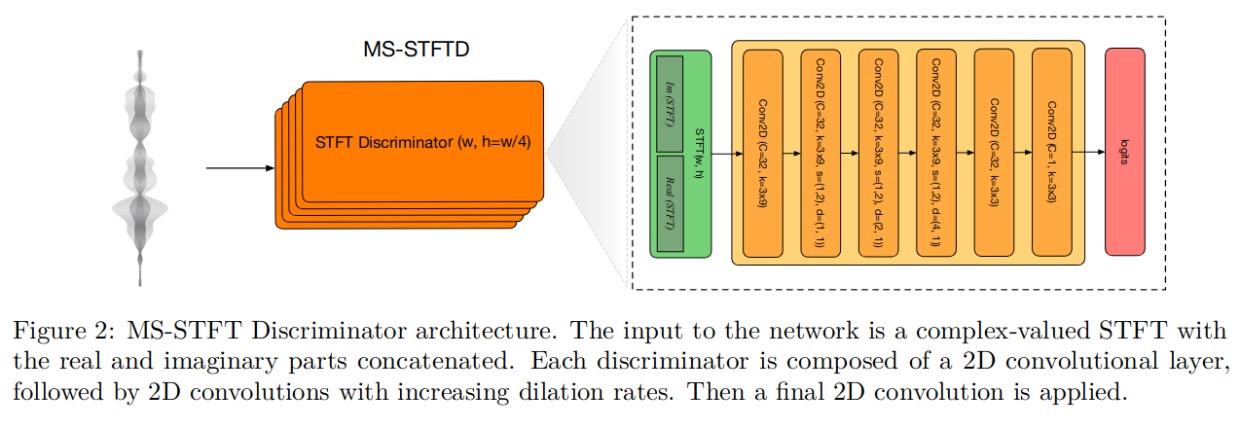
论文阅读_音频压缩_Encodec
论文信息 name_en: High Fidelity Neural Audio Compression name_ch: 高保真神经音频压缩 paper_addr: http://arxiv.org/abs/2210.13438 date_read: 2023-04-27 date_publish: 2022-10-24 tags: [‘深度学习’,‘音频’] author: Alexandre Dfossez, Meta AI, FAIR Team cod…...
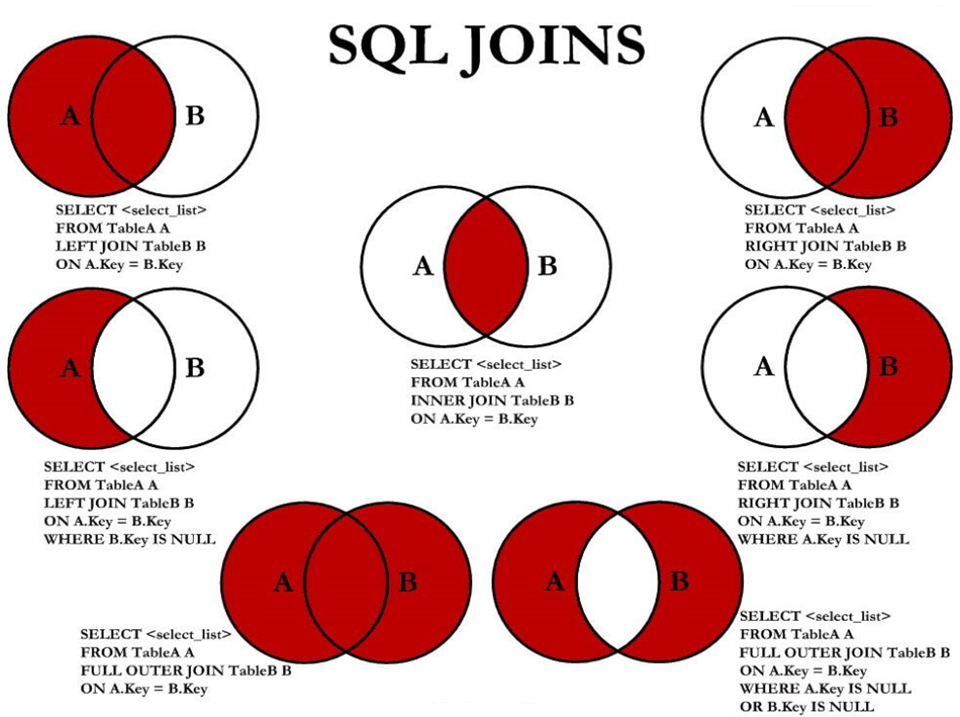
第06章_多表查询
第06章_多表查询 多表查询,也称为关联查询,指两个或更多个表一起完成查询操作。 前提条件:这些一起查询的表之间是有关系的(一对一、一对多),它们之间一定是有关联字段,这个关联字段可能建立了…...

自学黑客(网络安全)有哪些技巧——初学者篇
很多人说,要想学好黑客技术,首先你得真正热爱它。 热爱,听着多么让人激情澎湃,甚至热泪盈眶。 但很可惜,“热爱”这个词对还没入门的小白完全不管用。 如果一个人还没了解过你就说爱你,不是骗财就是骗色…...

CMD与DOS脚本编程【第四章】
预计更新 第一章. 简介和基础命令 1.1 介绍cmd/dos脚本语言的概念和基本语法 1.2 讲解常用的基础命令和参数,如echo、dir、cd等 第二章. 变量和运算符 2.1 讲解变量和常量的定义和使用方法 2.2 介绍不同类型的运算符和运算规则 第三章. 控制流程和条件语句 3.1 介…...

Liunx安装Docker
Liunx在线安装Docker 简介: Docker 是一个开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个可移植的容器中,然后发布到任何流行的 Linux 机器上,也可以实现虚拟化。容器是完全使用沙箱机制,相互之间不…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
