HNOI2014 世界树
洛谷P3233 [HNOI2014]世界树
题目大意
有一棵 n n n个点的树,每个点有一个编号,有 q q q次操作。对于每次操作,给出 m m m个点并称为议事点,树上各个点由离这个点最近的议事点管理(如果有多个议事点离这个点最近,则这个点由这些议事点中编号最小的点管理)。求每次操作中每个议事点管理的点的数目。
1 ≤ n ≤ 3 × 1 0 5 , 1 ≤ q ≤ 3 × 1 0 5 , 1 ≤ ∑ m i ≤ 3 × 1 0 5 1\leq n\leq 3\times 10^5,1\leq q\leq 3\times 10^5,1\leq \sum m_i\leq 3\times 10^5 1≤n≤3×105,1≤q≤3×105,1≤∑mi≤3×105
题解
前置知识:虚树
如果直接 d f s dfs dfs的话,则要通过两遍 d f s dfs dfs。对于一个非议事点 u u u,先用 u u u的子树中离 u u u最近的议事点来更新 u u u,再用 u u u的子树之外的离 u u u最近的议事点来更新 u u u。
下面是暴力的代码。
code
void dfs1(int u,int fa){dis[u]=inf;for(int i=r[u];i;i=l[i]){if(d[i]==fa) continue;dfs(d[i],u);if(dis[d[i]]+1<dis[u]){dis[u]=dis[d[i]]+1;to[u]=to[d[i]];}else if(dis[d[i]]+1==dis[u]){to[u]=min(to[u],to[d[i]]);}}if(z[u]){dis[u]=0;to[u]=u;}
}
void dfs2(int u,int fa){for(int i=r[u];i;i=l[i]){if(d[i]==fa) continue;if(dis[u]+1<dis[d[i]]){dis[d[i]]=dis[u]+1;to[d[i]]=to[u];}else if(dis[u]+1==dis[d[i]]){to[d[i]]=min(to[d[i]],to[u]);}dfs2(d[i],u);}z[u]=0;
}
因为 1 ≤ ∑ m i ≤ 3 × 1 0 5 1\leq \sum m_i\leq 3\times 10^5 1≤∑mi≤3×105,所以我们可以用虚树来解决问题。
对于每次操作,建一棵虚树。对于虚树上的点,用上面的 d f s dfs dfs跑一Bianc遍即可。
那不在虚树上的点怎么判断呢?
我们要分两种情况:
- 如果原树上有一个点 u u u,它有一个儿子 v v v,且 v v v的子树中没有议事点,则子树 v v v中的每个点肯定都是由离 u u u最近的议事点管理
- 如果虚树上有一个点 u u u,它有一个儿子 v v v,且 u u u和 v v v之间含有若干个点,则用倍增求 u u u和 v v v之间的这条链上的分界点,分界点及以下的部分由离 v v v最近的议事点管理,分界点以上的部分由离 u u u最近的议事点管理,注意链上附带的点也根据在分界点的上面或下面来判断由哪个议事点管理
对于第一种情况,在 d f s dfs dfs时对每个议事点的答案加上其子树的大小即可。
对于第二种情况,将分界点 x x x及以下的点的数量(即 s i z [ x ] − s i z [ v ] siz[x]-siz[v] siz[x]−siz[v])加在离 v v v最近的议事点上,将分界点以上的点的数量(因为在第一种情况中已经加上了每个议事点的子树大小,所以只需要减去 s i z [ x ] siz[x] siz[x])加在离 u u u最近的议事点上。
时间复杂度为 O ( n log n + ∑ m log m ) O(n\log n+\sum m\log m) O(nlogn+∑mlogm)。
code
#include<bits/stdc++.h>
using namespace std;
const int N=300005,inf=1e9;
int n,q,k,tot=0,wt=0,top=0,d[N*2],l[N*2],r[N*2],a[N],b[N];
int dep[N],dfn[N],siz[N],s[N],z[N],dis[N],to[N],ans[N],f[N][20];
vector<int>v[N];
int cmp(int ax,int bx){return dfn[ax]<dfn[bx];
}
void add(int xx,int yy){l[++tot]=r[xx];d[tot]=yy;r[xx]=tot;
}
void pt(int u,int fa){dfn[u]=++wt;dep[u]=dep[fa]+1;siz[u]=1;f[u][0]=fa;for(int i=1;i<=19;i++){f[u][i]=f[f[u][i-1]][i-1];}for(int i=r[u];i;i=l[i]){if(d[i]==fa) continue;pt(d[i],u);siz[u]+=siz[d[i]];}
}
int gt(int x,int y){if(dep[x]<dep[y]) swap(x,y);for(int i=19;i>=0;i--){if(dep[f[x][i]]>=dep[y]) x=f[x][i];}if(x==y) return x;for(int i=19;i>=0;i--){if(f[x][i]!=f[y][i]){x=f[x][i];y=f[y][i];}}return f[x][0];
}
void insert(int x){if(top==1){s[++top]=x;return;}int lca=gt(x,s[top]);while(top>1&&dfn[s[top-1]]>=dfn[lca]){v[s[top-1]].push_back(s[top]);--top;}if(s[top]!=lca){v[lca].push_back(s[top]);s[top]=lca;}s[++top]=x;
}
void dd(int x,int y){int u=y;for(int i=19;i>=0;i--){int v1,v2;v1=dep[y]-dep[f[u][i]]+dis[y];v2=dep[f[u][i]]-dep[x]+dis[x];if(dep[f[u][i]]>dep[x]&&(v1<v2||v1==v2&&to[y]<to[x])) u=f[u][i];}ans[to[y]]+=siz[u]-siz[y];ans[to[x]]-=siz[u];
}
void dfs1(int u,int fa){dis[u]=inf;for(int i=0;i<v[u].size();i++){int e=v[u][i];dfs1(e,u);int vt=dep[e]-dep[u];if(dis[e]+vt<dis[u]){dis[u]=dis[e]+vt;to[u]=to[e];}else if(dis[e]+vt==dis[u]){to[u]=min(to[u],to[e]);}}if(z[u]){dis[u]=0;to[u]=u;}
}
void dfs2(int u,int fa){for(int i=0;i<v[u].size();i++){int e=v[u][i];int vt=dep[e]-dep[u];if(dis[u]+vt<dis[e]){dis[e]=dis[u]+vt;to[e]=to[u];}else if(dis[u]+vt==dis[e]){to[e]=min(to[e],to[u]);}dd(u,e);dfs2(e,u);}ans[to[u]]+=siz[u];z[u]=0;v[u].clear();
}
int main()
{scanf("%d",&n);for(int i=1,x,y;i<n;i++){scanf("%d%d",&x,&y);add(x,y);add(y,x);}pt(1,0);scanf("%d",&q);while(q--){scanf("%d",&k);for(int i=1;i<=k;i++){scanf("%d",&a[i]);b[i]=a[i];z[a[i]]=1;ans[a[i]]=0;}sort(a+1,a+k+1,cmp);s[top=1]=1;for(int i=1;i<=k;i++){if(a[i]!=1) insert(a[i]);}while(top>1){v[s[top-1]].push_back(s[top]);--top;}dfs1(1,0);dfs2(1,0);for(int i=1;i<=k;i++){printf("%d ",ans[b[i]]);}printf("\n");}return 0;
}
相关文章:

HNOI2014 世界树
洛谷P3233 [HNOI2014]世界树 题目大意 有一棵 n n n个点的树,每个点有一个编号,有 q q q次操作。对于每次操作,给出 m m m个点并称为议事点,树上各个点由离这个点最近的议事点管理(如果有多个议事点离这个点最近&…...

在MyBatis XML文件中处理特殊符号的方法,如“>”、“<”、“>=”、“<=”这些符号XML会报错如何处理
前言 在MyBatis的XML映射文件中,我们经常需要使用特殊符号,比如"大于"、"小于"、"大于等于"、"小于等于"等比较操作符。然而,这些符号在XML中具有特殊的含义,因此需要进行特殊处理&…...

第三章--第一篇:什么是对话系统?
对话系统是一种人机交互的技术,旨在使计算机能够与人类进行自然而流畅的对话。它是人工智能领域的重要研究方向,具有重要的实际应用价值和广泛的普适性。 首先,对话系统的重要性在于它可以提供高效便捷的人机交互方式。传统的人机界面,如图形用户界面(GUI)和命令行界面(…...

项目基础搭建
一、项目创建 1.下载并安装nodejs 下载完成后,查看node版本 winR 快捷键,cmd确定,进入后台黑框 node -v查看npm安装路径 npm root -g安装cnpm镜像 npm install -g cnpm --registryhttps://registry.npm.taobao.org:查看npm版…...

PFCdocumentation_FISH Rules and Usage
目录 FISH Scripting FISH Rules and Usage Lines Data Types Reserved Names for Functions and Variables Scope of Variables Functions: Structure, Evaluation, and Calling Scheme Arithmetic: Expressions and Type Conversions Redefining FISH Functions Ex…...
如何完美卸载VS2015(2023年5月份实测有效)
使用控制面板卸载VS2015,出现正在配置您的系统,这可能需要一些时间,然后就出现卡住半个小时第二行的条都没有动的问题,这里提供vs2015以及以前版本的卸载方式 问题产生原因:他需要下载一些东西,然后由于你懂的网络原因…...

JavaScript如何声明和定义函数
JavaScript是一门非常有趣的编程语言,它可以让我们创建各种各样的函数来解决各种各样的问题。在JavaScript中,函数的声明和定义非常重要,因为它们决定了函数的行为和执行过程。 首先,让我们来看看JavaScript中函数的声明。在Java…...

微信小程序 WebSocket 通信 —— 在线聊天
在Node栏目就讲到了Socket通信的内容,使用Node实现Socke通信,还使用两个流行的WebSocket 库,ws 和 socket.io,在小程序中的WebSocket接口和HTML5的WebSocket基本相同,可以实现浏览器与服务器之间的全双工通信。那么本篇…...
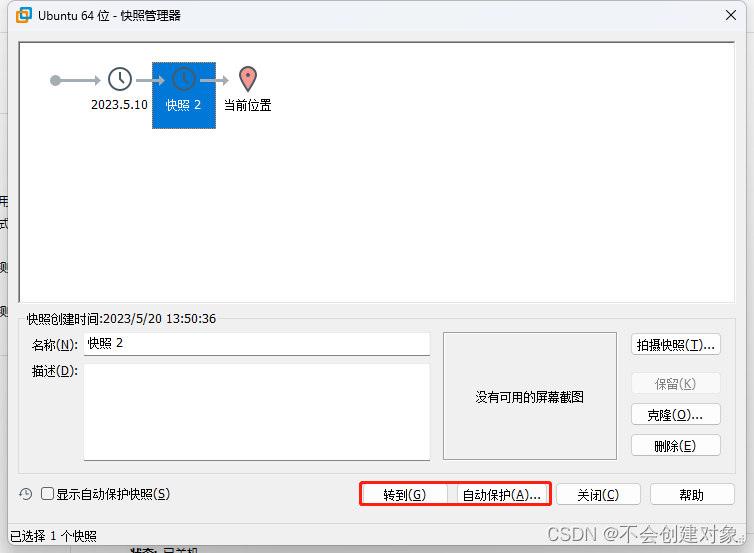
VMware快照:简化虚拟化环境管理与数据保护
引言: 在虚拟化环境中,数据保护和灵活性是至关重要的。VMware快照作为一项强大的功能,为虚拟机管理者提供了便利和安全性。本文将介绍VMware快照的使用,以及它为用户带来的几个关键优势。 VMware快照是一项重要的功能,…...
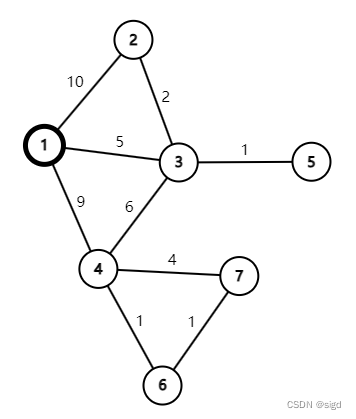
图的最短路径
最短路径算法对图结构没有特殊要求,不要求连通图,且有向图无向图均可。 最短路径算法目标是求得从某顶点出发,沿图的边到达另一顶点所经过的路径中,各边上权值之和最小的一条路径。解决最短路的问题有以下算法:Dijkst…...

RHCE----Shell变量和引用
1.变量的类型及含义 变量类型: 1、自定义变量: 在当前的shell命令行界面设置的变量是局部变量 例子: num1 namezhangsan 2、环境变量全局变量,通过export 导出后的局部变量是全局变量 、bash的初始化文件:/etc/profile:存放一些全局变量…...
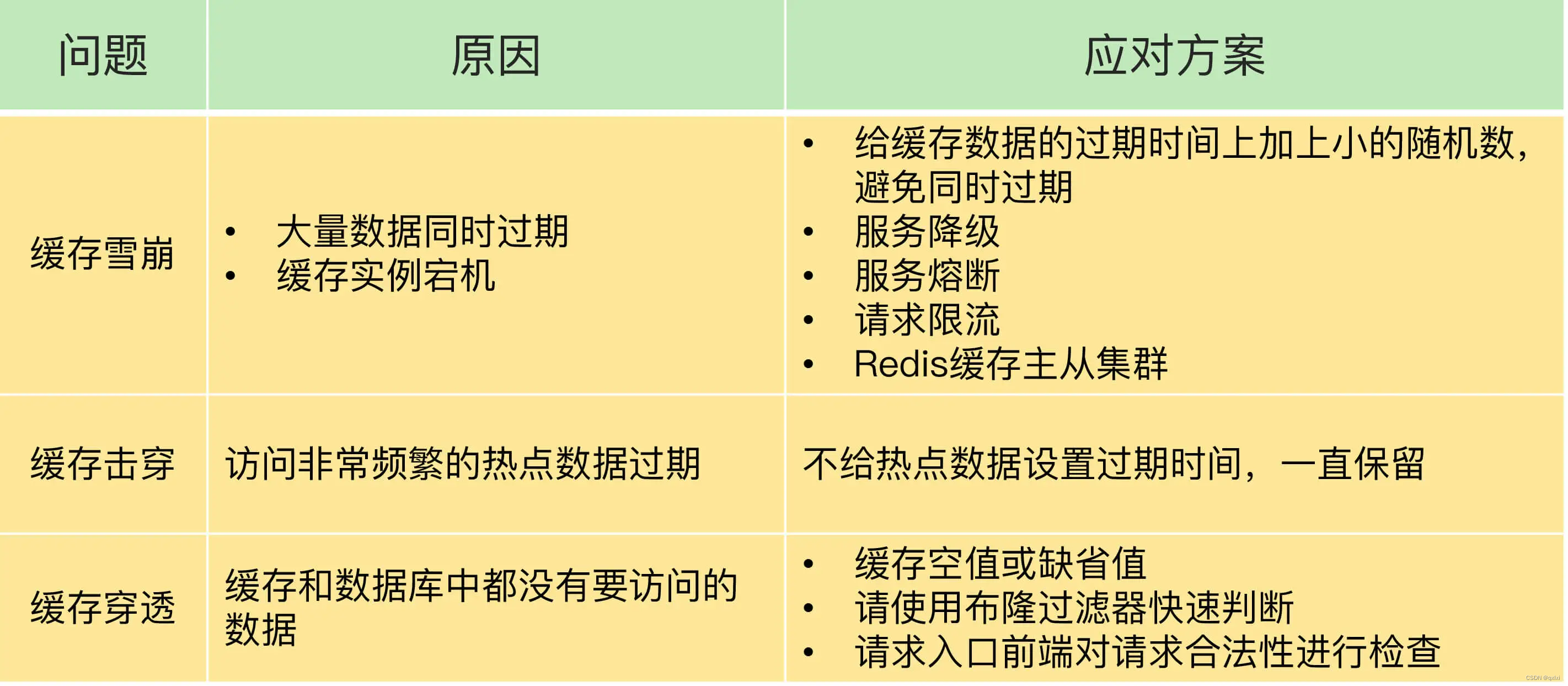
【Redis】聊一下缓存雪崩、击穿、穿透、预热
缓存的引入带来了数据读取性能的提升,但是因此也引入新的问题,一个是数据双写一致性,另一个就是雪崩、击穿、穿透,那么如何解决这些问题,我们来说下对应的问题和解决方案 雪崩 缓存雪崩:同一时间内大量请…...

全景描绘云原生技术图谱,首个《云原生应用引擎技术发展白皮书》发布
5月12日,由神州数码主办、北京经开区国家信创园、中关村云计算产业联盟协办的2023通明湖论坛-云原生分论坛在京召开。论坛期间,神州数码联合北京通明湖信息技术应用创新中心、中国信通院和通明智云正式发布了《云原生应用引擎技术发展白皮书》࿰…...
【Python共享文件】——Python快速搭建HTTP web服务实现文件共享并公网远程访问
文章目录 1. 前言2. 视频教程3. 本地文件服务器搭建3.1 python的安装和设置3.2 cpolar的安装和注册 4. 本地文件服务器的发布4.1 Cpolar云端设置4.2 Cpolar本地设置 5. 公网访问测试6. 结语 1. 前言 数据共享作为和连接作为互联网的基础应用,不仅在商业和办公场景有…...

Mysql数据库分库分表
为什么使用分库分表? 传统的将数据集中存储至单一数据节点的解决方案,在性能、可用性和运维成本这三方面已经难于满足互联网的海量数据场景。 1)性能 从性能方面来说,由于关系型数据库大多采用 B 树类型的索引,在数…...
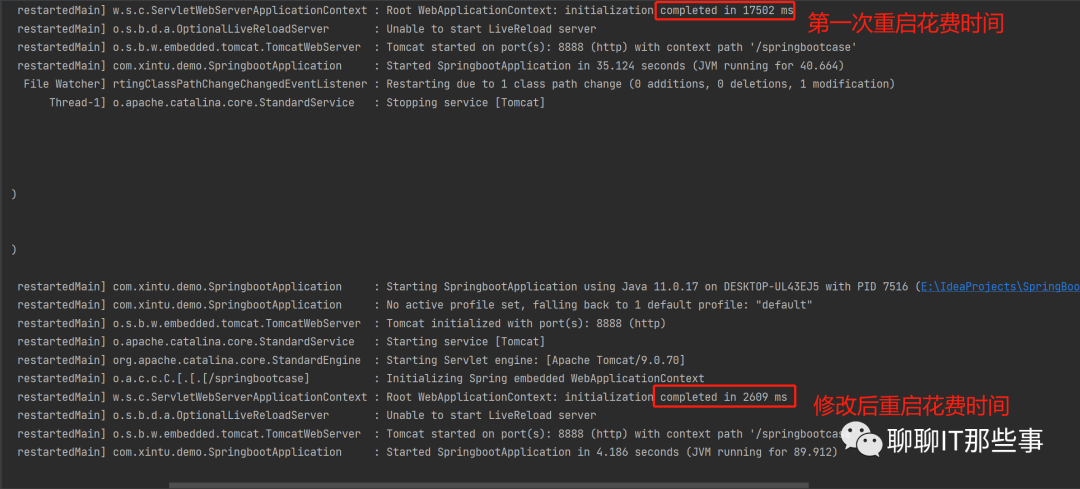
SpringBoot热部署插件原理分析及实战演练
目录 1、关于热部署(Hot Deploy)产生的背景 1)热部署出现前 2)热部署出现后 2、spring-boot-devtools插件原理 1)解决变更文件自动加载到JVM中 2)spring-boot-devtools重启速度比手动重启快 3、关于…...

【C++ 入坑指南】(10)函数
文章目录 简介定义实例函数的分文件编写 简介 函数是一组一起执行一个任务的语句。每个 C 程序都至少有一个函数,即主函数 main() ,所有简单的程序都可以定义其他额外的函数。 您可以把代码划分到不同的函数中。如何划分代码到不同的函数中是由您来决定…...
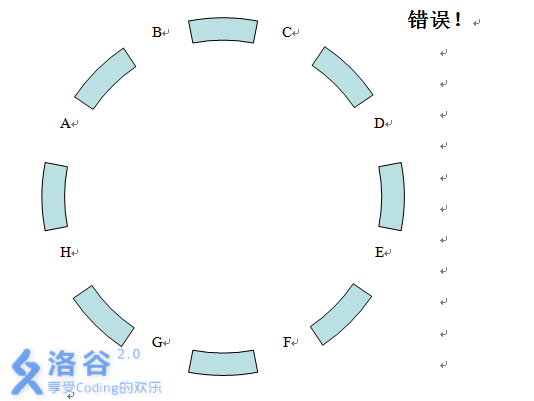
P2233 [HNOI2002]公交车路线
题目描述 在长沙城新建的环城公路上一共有 8 个公交站,分别为 A、B、C、D、E、F、G、H。公共汽车只能够在相邻的两个公交站之间运行,因此你从某一个公交站到另外一个公交站往往要换几次车,例如从公交站 A 到公交站 D,你就至少需要…...
网络编程)
java入门-W11(K168-K182)网络编程
1. 网络编程入门 1.1 网络编程概述 计算机网络 是指将地理位置不同的具有独立功能的多台计算机及其外部设备,通过通信线路连接起来,在网络操作系统,网络管理软件及网络通信协议的管理和协调下,实现资源共享和信息传递的计算机系统…...

距离6月18日DAMA-CDGA/CDGP认证考试还有31天,报名从速
6月18日DAMA-CDGA/CDGP数据治理认证考试开放报名中! 考试开放地区:北京、上海、广州、深圳、长沙、呼和浩特、杭州、南京、济南、成都、西安。其他地区凑人数中… DAMA-CDGA/CDGP数据治理认证班进行中,报名从速! DAMA认证为数据管…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
