C语言递归算法实现经典例题
一.递归
1.什么是递归
递归是一种编程技术,它通过在函数内部反复调用自身来解决问题。当一个程序调用自己时,这就称为递归调用。递归可以有助于简化某些算法的实现和理解。在递归过程中,每个调用都会将一些数据保存在栈上,直到递归结束后才能被处理并弹出栈。
递归通常有两个部分:基本情况和递归情况。基本情况是在函数执行之前判断是否需要递归,如果不需要,则直接返回结果。递归情况是函数需要递归时,它会调用自身,但是传入的参数通常会有所不同,以便最终能够达到基本情况而结束递归。
虽然递归可以使代码更加简洁,但是需要注意的是,在一些情况下,它可能会导致性能问题或者栈溢出等问题。因此,在编写递归代码时,需要仔细考虑算法的边界条件和递归深度等因素。
2.递归函数
递归函数是一种函数,它在其定义中调用自身。通常情况下,递归函数包含两个部分:基本情况和递归情况。
基本情况是指在递归函数中需要判断是否需要终止递归的条件。当满足这个条件时,递归就会停止。
递归情况是指在递归函数中需要调用自身的情况。在每次调用时,函数的参数都应该有所不同,以便最终能够达到基本情况而停止递归。
递归函数通常用于处理树形结构、图形结构或其他类型的嵌套结构数据。例如,在二叉树中查找某一个值,就可以使用递归函数来实现。
3.说明
虽然递归算法比较简单,但是它是一种编程的思想,在解决部分问题时,它非常适用。并且他一般作为一种工具,搭配其他思想一起使用。它是C语言数据结构与算法中最简单的算法,这里举几个例子来学会使用它。
二.斐波那契数列
1.问题描述
斐波那契数列是一个经典的数学问题,由0和1开始,之后的每一项都是其前面两项的和。也就是说,斐波那契数列的前几个数是:0、1、1、2、3、5、8、13、21、34……依次类推。
斐波那契数列在自然界中有很多应用,比如植物的叶子排列、蜂窝的构造等等。除此之外,在计算机科学领域内,斐波那契数列也有着广泛的应用,例如在排序算法、密码学等领域。
斐波那契数列的通项公式是:F(n) = F(n-1) + F(n-2),其中F(0)=0,F(1)=1。根据这个公式可以使用递归函数或循环语句来实现求斐波那契数列的第n项。
2.思路
像这种可以求出通项公式的数列是我们平时典型的递归函数运用,通项公式可以定义为函数,它的第一个值一般是我们的递归函数出口。所谓递归函数的出口就是结束递归的标志。
现在理清思路后,我们来用代码完成求斐波拉契数列的第n项:
3.C语言代码
#include <stdio.h>int fibonacci(int n) {if (n == 0)return 0;else if (n == 1)return 1;elsereturn fibonacci(n - 1) + fibonacci(n - 2);
}int main() {int num, i;printf("Enter the number of terms: ");scanf("%d", &num);printf("Fibonacci series terms are:\n");for (i = 0; i < num; i++) {printf("%d ", fibonacci(i));}printf("\n");return 0;
}三.汉诺塔
1.问题描述
该问题的主要材料包括三根高度相同的柱子和一些大小及颜色不同的圆盘,三根柱子分别为起始柱A,辅助柱B及目标柱C。
**操作规则:**每次只能移动一个盘子,并且在移动过程中三根杆上都始终保持大盘在下,小盘在上,操作过程中盘子可以置于任意杆上。
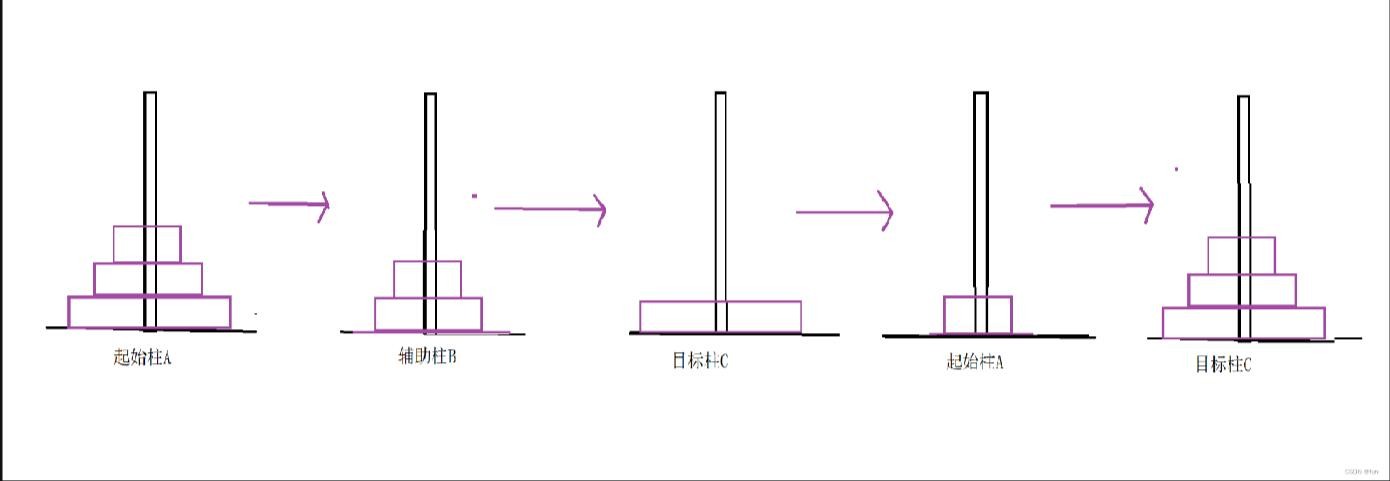
2.分析
汉诺塔是一种经典的递归问题,它涉及到将一组不同大小的圆盘从一个柱子移动到另一个柱子。以下是汉诺塔的具体过程:
- 将所有圆盘从起始柱子上除最下面一个圆盘之外的其他圆盘全部移动到中间柱子。
- 将最下面的圆盘从起始柱子上移动到目标柱子上。
- 将中间柱子上除了最下面的圆盘之外的其他圆盘全部移动到目标柱子上。
在完成这三个步骤时,需要遵守以下规则:
- 一次只能移动一个圆盘。
- 大圆盘不能放在小圆盘上面。
通过递归调用上述步骤,可以将所有的圆盘从起始柱子移动到目标柱子。由于每次递归都会将一个圆盘从起始柱子移动到目标柱子,因此每个圆盘最多只会被移动一次,所以总共需要移动2^n - 1 次(n 表示圆盘的数量)。
3.C语言代码
#include <stdio.h>void hanoi(int n, char A, char B, char C) {if (n == 1) {printf("Move disk 1 from %c to %c\n", A, C);} else {hanoi(n-1, A, C, B);printf("Move disk %d from %c to %c\n", n, A, C);hanoi(n-1, B, A, C);}
}int main() {int n = 3; // 将3个盘子从A移动到Chanoi(n, 'A', 'B', 'C');return 0;
}四.子集问题
1.问题描述
子集问题(Subset):给定一个含有n个元素的集合S,求出S的所有子集。可以使用递归实现。
2.思路分析
子集问题是一个基本的组合问题,它涉及到从一个给定的集合中选择一些元素组成新的集合。这个问题在计算机科学和数学中非常常见,解决子集问题可以帮助我们更好地理解组合问题和算法设计。
下面是一个简单的思路分析:
-
首先,我们需要确定如何表示集合。在大多数编程语言中,集合通常是用数组或列表来表示的。
-
接着,我们需要考虑如何生成所有可能的子集。一种常见的方法是使用递归算法。
-
对于递归算法,我们需要考虑以下几点:
a. 基本情况:当集合为空时,只有一个空集。
b. 递归情况:对于非空集合,我们可以选择将第一个元素包含在子集中或者不包含在子集中,然后对剩余的元素进行递归处理。
-
在递归过程中,我们需要维护一个当前子集的列表,并在每次递归结束后将其添加到结果集合中。
-
最后,我们可以返回结果集合,其中包含了原始集合的所有可能子集。
需要注意的是,由于子集问题的解空间非常大,因此在实际应用中,需要根据具体的场景进行优化,以减少时间和空间复杂度。
3.C语言代码
下面是一个使用C语言递归实现子集问题的示例代码:
#include <stdio.h>void subset(int set[], int subset[], int n, int k, int start, int curr){if (curr == k) {printf("{");for (int i = 0; i < k; i++) {printf("%d ", subset[i]);}printf("}\n");return;}for (int i = start; i < n; i++){subset[curr] = set[i];subset(set, subset, n, k, i+1, curr+1);}
}int main() {int set[] = {1, 2, 3};int n = sizeof(set)/sizeof(set[0]);int subset[n];for (int i = 0; i <= n; i++) {subset(set, subset, n, i, 0, 0);}return 0;
}
该代码中,subset函数使用了递归实现。其中,set表示原始集合,subset表示当前子集,n表示原始集合的大小,k表示当前子集的大小,start表示遍历起始位置,curr表示当前子集中元素的个数。
在函数中,首先判断当前子集是否已达到目标大小 k,如果已经达到则输出该子集,并返回上一层递归。否则,从遍历起始位置开始循环原始集合,将元素依次加入当前子集,并对剩余元素进行递归处理。
在 main 函数中,我们遍历所有可能的子集大小,并调用 subset 函数进行求解。最终结果会依次输出到标准输出。
五.归并排序
1.问题描述与分析
归并排序(Merge Sort)是一种基于分治思想的高效排序算法,通过将待排序数组递归地拆分为两个子数组,对每个子数组进行排序,然后将两个有序的子数组合并成一个有序的数组,最终得到排序完成的整个数组。
具体而言,归并排序的过程可以分为三个步骤:
- 分割:将待排序数组从中间位置划分为左右两个子数组,递归地对左右两个子数组进行分割,直到每个子数组只包含一个元素。
- 归并:将两个有序的子数组合并成一个有序的数组,直到所有子数组都被合并为一个完整的有序数组。
- 返回:返回排序完成的数组。
2.C语言代码
下面是用 C 语言递归实现归并排序的代码:
#include <stdio.h>
#include <stdlib.h>void merge(int *arr, int l, int m, int r) {int i, j, k;int n1 = m - l + 1;int n2 = r - m;int L[n1], R[n2];for (i = 0; i < n1; i++)L[i] = arr[l + i];for (j = 0; j < n2; j++)R[j] = arr[m + 1 + j];i = 0;j = 0;k = l;while (i < n1 && j < n2) {if (L[i] <= R[j]) {arr[k] = L[i];i++;} else {arr[k] = R[j];j++;}k++;}while (i < n1) {arr[k] = L[i];i++;k++;}while (j < n2) {arr[k] = R[j];j++;k++;}
}void mergeSort(int *arr, int l, int r) {if (l < r) {int m = l + (r - l) / 2;mergeSort(arr, l, m);mergeSort(arr, m + 1, r);merge(arr, l, m, r);}
}int main() {int arr[] = {38, 27, 43, 3, 9, 82, 10};int n = sizeof(arr) / sizeof(arr[0]);mergeSort(arr, 0, n - 1);for (int i = 0; i < n; i++)printf("%d ", arr[i]);return 0;
}
在上面的代码中,merge 函数用于将两个有序子数组合并为一个有序数组,mergeSort 函数用于递归地分割和排序子数组。
六.说明
新星计划:数据结构与算法,@西安第一深情,创作打卡1!
相关文章:

C语言递归算法实现经典例题
一.递归 1.什么是递归 递归是一种编程技术,它通过在函数内部反复调用自身来解决问题。当一个程序调用自己时,这就称为递归调用。递归可以有助于简化某些算法的实现和理解。在递归过程中,每个调用都会将一些数据保存在栈上,直到递…...
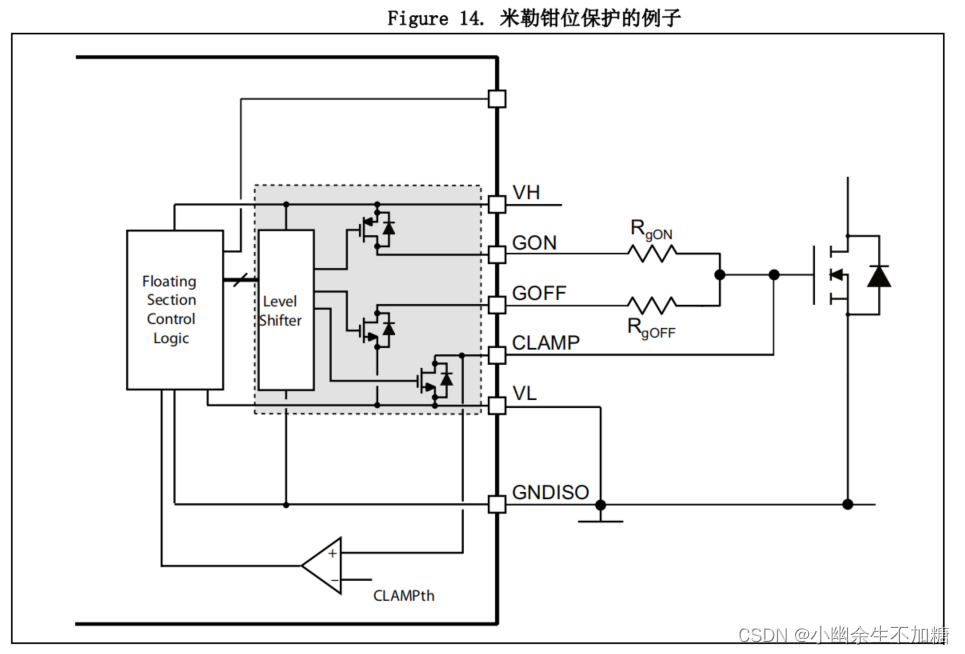
ST典型碳化硅MOSFET驱动应用方案
ST典型碳化硅MOSFET驱动应用方案 1.栅极驱动器规格和功能实现 参考资料:ST官网应用手册《AN4671》 作者:Xiou 1.栅极驱动器规格和功能实现 以下是对栅极驱动要求的简短列表: dv / dt 的瞬变抗扰度:在整个温度范围内 50 V/ns。 …...

对比AMD和英特尔显卡的区别
✨求关注~ 😀博客:www.protaos.com AMD和英特尔都是著名的半导体公司,它们都生产处理器和显卡。在显卡领域,AMD生产Radeon系列显卡,而英特尔则生产Intel HD Graphics和Intel Iris Graphics系列显卡。 使用群体对比&…...

Linux系统c语言socket实现UDP通信
UDP全称 User Datagram Protocol,即:用户数据报协议。是面向无连接的协议。通常,UDP 通信还会被冠以不可靠的头衔。这里的不可靠指的是:无法可靠地得知对方是否收到数据。 UDP有如下特征: 无连接:通信双方不需要事先连接无确认:收到数据不给对方发回执确认不保证有序、丢…...

常用五大类RFID系统,实践领域广泛,加强现代化管理
随着信息技术的不断进步,RFID技术已逐渐成为企业管理及社会服务领域中不可或缺的一种重要技术手段。根据其不同的应用场景,RFID技术广泛应用于药品监管、固定资产管理、仓储管理、智慧工厂和消费服务等领域。本文将从五个方面介绍常用的RFID系统。 一、…...
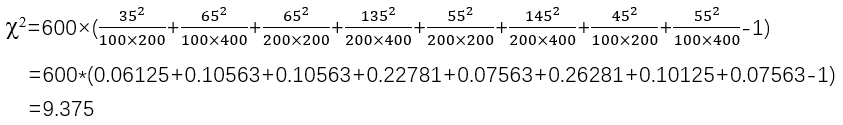
卡方检验.医学统计实例详解
卡方检验是一种常用的假设检验方法,通常用于分析两个或多个分类变量之间的关系。在医学研究中,卡方检验被广泛应用于分析两种或多种治疗方法的疗效,或者分析某种疾病的发病率与某些危险因素之间的关系。下面我们来看一个卡方检验在医学实例中…...

H264和AAC打包PS包代码
段老师的干货时间又到咯,下面代码实现的是将 AAC 和 H264 数据打包成 PS 包的流程,其中包括了 PES 头、PSI 表头、MPEG-TS 头、AAC/H264 数据打包等多个步骤。此外,还包含 CRC32 校验等校验码的计算。需要注意的是,此代码示例仅供…...

Redis数据类型-ZSet
一. 概述 SortedSet又叫zset,它是Redis提供的特殊数据类型,是一种特殊的set类型,继承了set不可重复的特点,并在set基础上为每个值添加一个分数,用来实现值的有序排列。 二. 常用指令 明白它的特点后,接下来…...

国外各大学和学院对于ChatGPT使用立场总结
ChatGPT和生成式AI的快速普及对教育这个专业领域带来了威胁——全国各地的大学和学院都召开了紧急会议,讨论如何应对学生利用AI作弊的风险。 一部分学校和教授担心这项技术会成为学生在论文或其他写作作业和考试中寻求捷径的工具。而这种生成内容的方式往往能够绕开…...
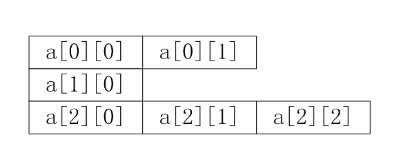
我在VScode学Java(Java二维数组)
我的个人博客主页:如果\真能转义1️⃣说1️⃣的博客主页 关于Java基本语法学习---->可以参考我的这篇博客:(我在Vscode学Java) 接上回Java一维数组的介绍(我在VScode学Java(Java一维数组) ) 二维数组是Java中的一…...
HTML-iconfont动态图标SVG效果--阿里巴巴图标矢量库
给北大打工,实现官网首页动态图标效果_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1Ys4y1c7oh/?spm_id_from333.1007.top_right_bar_window_default_collection.content.click&vd_source924f5dad6f2dcb0a3e5dca4604287ecd(本篇笔记操作方法…...

C++17完整导引-模板特性之编译器的if语句
编译期if语句 if constexpr 编译期if语句使用编译期if语句编译期if的注意事项编译期if影响返回值类型即使在 *then* 部分返回也要考虑 *else* 部分编译期短路求值 其他编译期if的示例完美返回泛型值使用编译期if进行类型分发 带初始化的编译期if语句在模板之外使用编译期if参考…...
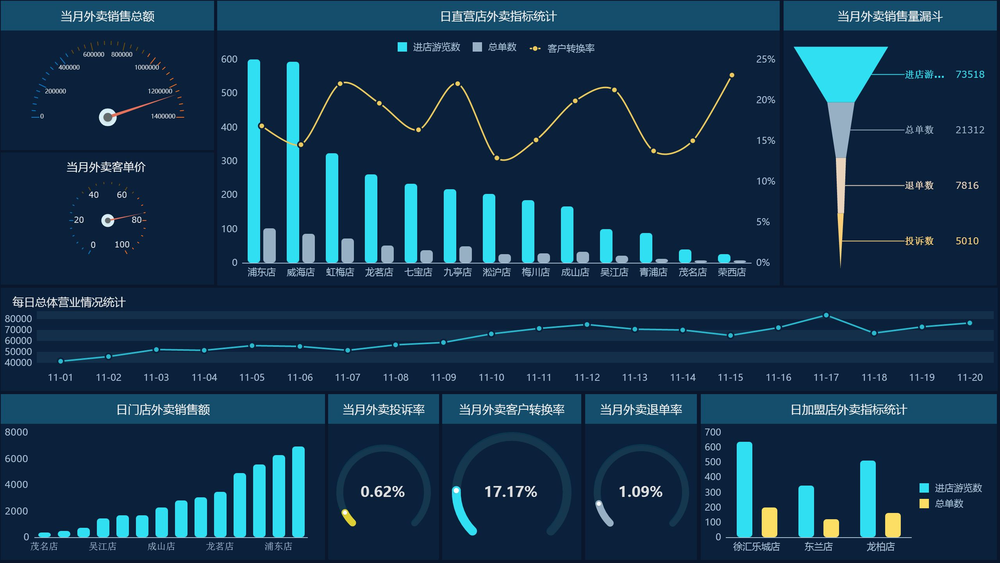
告别Excel,免费大数据分析与可视化工具,让你的论文图表“高大上”
数据分析工具很多,可以分为表格、数据库、BI工具、编程等四大工具。每个大类又有很多的工具,例如表格包括Excel、WPS、Google Sheets、Airtable等。编程工具包括Python和R。 搞科研几年了,笔者一直都是在使用Excel做数据分析和可视化…...

C++ 中的继承和多态
C 中的继承和多态 一、继承二、函数重载、隐藏、覆盖、重写1.函数重载(Function Overload)2.函数隐藏(Function Hiding)3.函数重写与函数覆盖(Function Override) 三、多态四、纯虚函数和抽象类五、多重继承…...
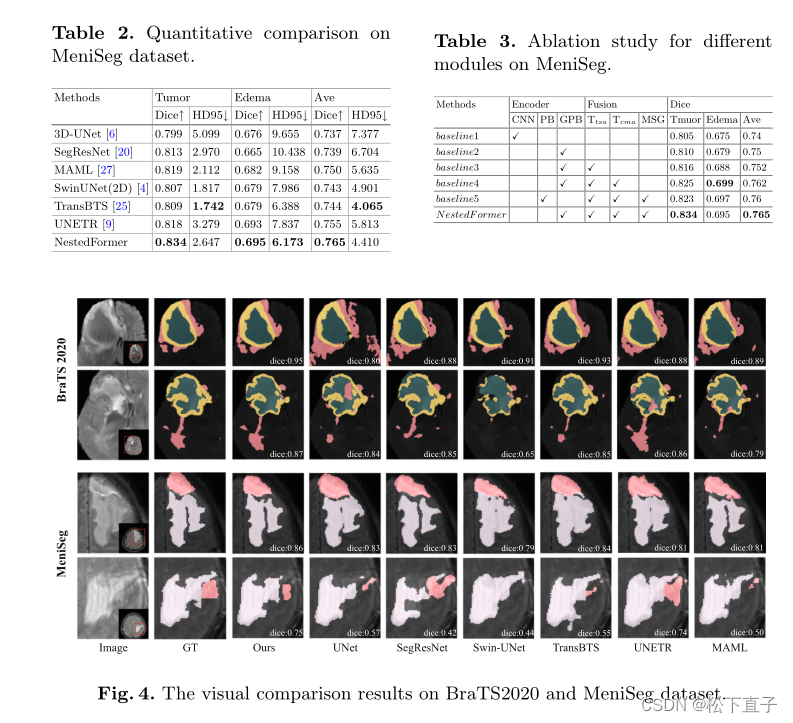
NestedFormer:用于脑肿瘤分割的嵌套模态感知Transformer
文章目录 NestedFormer: Nested Modality-AwareTransformer for Brain Tumor Segmentation摘要方法Global Poolformer EncoderNested Modality-Aware Feature AggregationModality-Sensitive Gating 实验结果 NestedFormer: Nested Modality-AwareTransformer for Brain Tumor …...
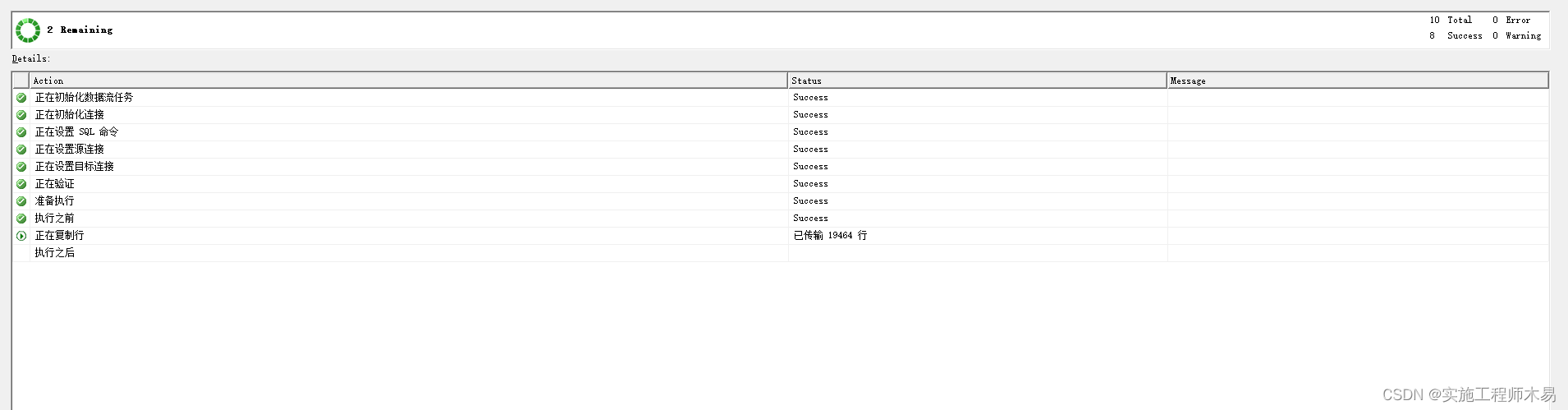
【SQLServer】sqlserver数据库导入oracle
将sqlserver数据库导入到oracle 实用工具: SQL Server Management Studio 15.0.18424.0 SQL Server 管理对象 (SMO) 16.100.47021.07eef34a564af48c5b0cf0d617a65fd77f06c3eb1 Microsoft Analysis Services 客户端工具 15.0.19750.0 Microsoft 数据访问组件 (MDAC) …...

【5.20】四、性能测试—性能测试工具
目录 4.5 性能测试工具 4.5.1 LoadRunner 4.5.2 JMeter 4.5 性能测试工具 性能测试是软件测试中一个很重要的分支,人们为了提高性能测试的效率,开发出了很多性能测试工具。一款好的测试工具可以极大地提高测试效率,为发现软件缺陷提供重要…...
)
朗诵素材-《少年正是读书时》(两角色主持朗诵)
少年正是读书时 1、少年正是读书时 男:我们生活在/古老的土地上 男:我们拥有/共同的梦想 女:那朗朗的书声/那浓浓的墨香 女:都在告诉我们 合:少年正是/读书时 2、为何要读书 男:养心&am…...

凭借这个笔记,拿下8家大厂offer....
如何拿到多家大厂的offer,没有过硬的实力,就需要不断的学习。 我是如何拿到,阿里,腾讯,百度等八家大厂的offer的,今天我就给大家来分享我的秘密武器,阿里大神整理的包括,测试基础&am…...
介绍一下全链路压测平台的相关内容
随着互联网技术的不断发展,越来越多的企业开始依赖互联网来实现业务的发展和增长。而对于这些企业而言,如何保证他们的业务在高并发、高负载的情况下依然能够正常运行,是非常重要的一个问题。为了解决这个问题,企业可以使用全链路…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
