LeeCode [N字形变换]算法解析
关键字:数学归纳法
一、题目
将一个给定字符串
s根据给定的行数numRows,以从上往下、从左到右进行 Z 字形排列。比如输入字符串为
"PAYPALISHIRING"行数为3时,排列如下:
P A H N A P L S I I G Y I R
之后,你的输出需要从左往右逐行读取,产生出一个新的字符串,
比如:
"PAHNAPLSIIGYIR"。请你实现这个将字符串进行指定行数变换的函数:
convert(s, numRows);示例 1:
输入:s = "PAYPALISHIRING", numRows = 3
输出:"PAHNAPLSIIGYIR"示例 2:
输入:s = "PAYPALISHIRING", numRows = 4
输出:"PINALSIGYAHRPI"
解释:
P I N
A L S I G
Y A H R
P I示例 3:
输入:s = "A", numRows = 1
输出:"A"二、思路:使用数学归纳法对Z字形排列进行规律总结
// 3阶Z变形 7个1
// 1 1
// 1 1 1
// 1 1
// 4阶Z变形 10个1
// 1 1
// 1 1 1
// 1 1 1
// 1 1
// 5阶Z变形 13个1
// 1 1
// 1 1 1
// 1 1 1
// 1 1 1
// 1 1
// ........
// n阶Z变形
// 得到公式,n阶:3n-2个1,3n - 2 = n + (n-2) + n
经过以上归纳,我们知道了对于Z字变形的一个数学上的规律,这里的n就是题目中的numRows变量。同时从图形上看,我们可以把一个V形看成一个周期(如下图,表示3个周期),确定这个思想有利于理解后面的逻辑。
1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1
三、现在我们知道了这样一个规律,那么我们很容易想到把字符串按照这样的规律放进到一个二维数组里面,所以,我们需要基于我们发现的规律来分析出两个关键点:
- 二维数组的行列数
- 每一个字符在二维数组中的位置
四、实现步骤
1、定义一个二维数组,二维数组为arr[n-1][m-1],n为行数,m为列数,s为字符串
m = (Math.floor(s.length / (2n-2)))*(n-1) + (s.length % (2n-2)-n>0?(n-2)+1:(s.length % (2n-2) === 0?0:1);这里把(n + (n-2))看成一个周期
// 粗略一点的话,m也可以直接等于 Math.ceil(s.length/(2n - 2))*(n-1)
2、每个字符在二维数组中的位置(同样用到了数学归纳法)
假设字符的索引为i:
所在列:col = (Math.floor((i+1) / (2n-2)))*(n-1) + ((i+1) % (2n-2)-n>0?(n-2)+1:((i+1) % (2n-2) === 0?0:1)
所在行:row = (i+1)%(2n-2) <=n?((i+1)%(2n-2)===0?2:(i+1)%(2n-2)):2n-(i+1)%(2n-2)
3、 遍历字符串,把每个字符放在对应的位置上
4、再按行,从左到右取字符
五、完整代码
let convert = function(s,numRows = 3){let n = numRows;let len = s.length;let m = 0let arr = new Array(n);if(len < (3 * numRows - 2)){return s}m = (Math.floor(len/(2*n-2)))*(n-1)let remainder = len%(2*n-2)if(remainder !== 0){m += (remainder - n > 0?(n-2)+1:1)}for(let i = 0;i < n;i++){arr[i] = new Array(m);}// 遍历字符串for(let i = 0;i < len;i++){let remainder1 = (i+1)%(2*n-2)let col = (Math.floor((i+1)/(2*n-2)))*(n-1) + (remainder1-n>0?(n-2)+1:(remainder1 === 0?0:1))col = col -1 // 从0列开始let row = remainder1 <= n?remainder1:2*n-remainder1if(remainder1 === 0){row = 2}row = row - 1 // 从0行开始arr[row][col] = s[i]}// 按行从左向右取字符串let result = '';for(let i = 0;i < n;i++){for(let j = 0;j < m;j++){if(arr[i][j]){result += arr[i][j]}}}console.log(arr)console.log(result)
}
convert("PAYPALISHIRING",3) //输出:PAHNAPLSIIGYIR
convert("PAYPALISHIRING",4) //输出:PINALSIGYAHRPI相关文章:

LeeCode [N字形变换]算法解析
关键字:数学归纳法 一、题目 将一个给定字符串 s 根据给定的行数 numRows ,以从上往下、从左到右进行 Z 字形排列。 比如输入字符串为 "PAYPALISHIRING" 行数为 3 时,排列如下: P A H N A P L S I I G Y I R …...

CPU性能提升:流水线
一条指令的执行一般要经过取指令,翻译指令,执行指令3个基本流程。CPU内部的电路分为不同的单元,取指但愿,译码单元,执行单元等。指令的执行也是按照流水线工序一步步执行的。如图2-34所示,我们假设每一个步…...

C语言指针初级
目录 一、什么是指针 二、指针和指针类型 三、野指针 1.野指针的成因: 2.如何规避野指针 四、指针运算 1.指针-整数 2. 指针之间的加减 五、二级指针 六、指针数组 一个男人,到底要走多少的路,才能成为一个真正的男人 本专栏适用于…...

C++的历史
C是一种广泛使用的编程语言。C于1983年由丹尼斯里奇(Dennis Ritchie)在贝尔实验室创造,它是C语言的扩展。C的设计初衷是为了提高代码的可重用性和可维护性。它允许开发人员使用面向对象编程(OOP)范例,这使得…...
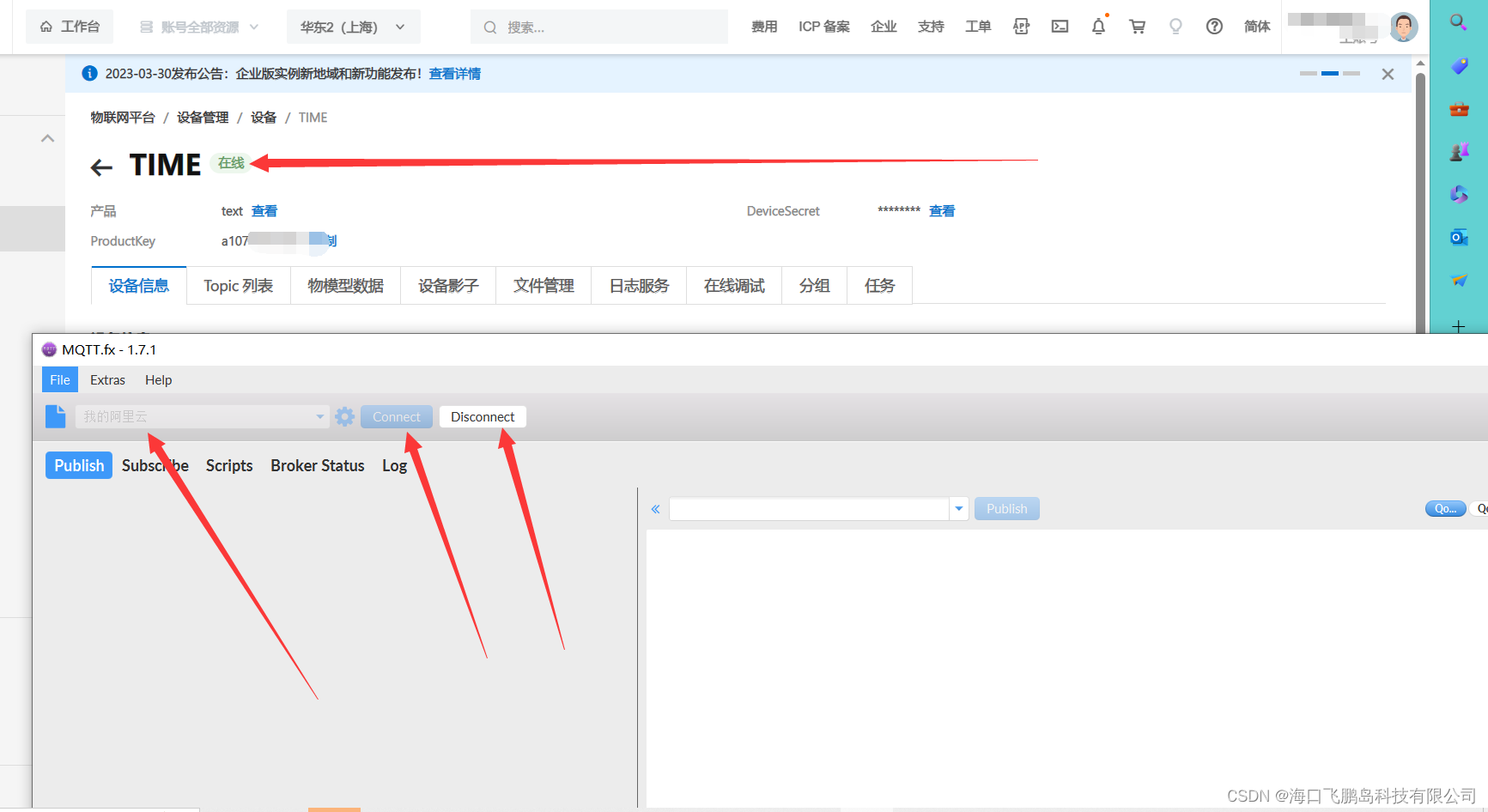
保姆级别!!!--全网绝对教你会!!教你如何使用MQTTFX连接阿里云平台中的设备----下期告诉你如何创建!
本期需要下载的软件 MQttfx安装包,本人打包的-嵌入式文档类资源-CSDN文库 目录 第一步:建造阿里云设备 这个可以先忽略建造步骤,下期将提供步骤。 第二步:下载mqttfx软件 第三步:填写密钥信息进行连接 查看三元…...

Unexpected token ‘‘‘, “‘{“type“:““... is not valid JSON
尝试低代码schema解析JSON时报错,奇怪的是控制台解析正常,项目js执行JSON.parse()报错,简直无语了,,, 只能挨个检查了,首先温习了下JSON 的标准格式: JSON的合法符号:{(左大括号) }(右大括号) "(双引号) :(冒号) ,(逗号) [(左中括号) ](右中括号) JSON字符串:…...

关于C语言的杂记5
文章目录 引入正文内部函数与外部函数相关数组的知识点数组的初始化测试一维数组在内存中存储的地址:遍历二维数组的值测试二维数组的地址(观察内存情况)数组下标为0开始的由来 两个数交换位置的三种方法 引入 写在前面:关于C语言这部分内容,…...

YOLOv5 vs YOLOv6 vs YOLOv7目标检测模型速度和准确度的性能比较——深入研究
如果您正在进行目标检测项目,您很可能会选择众多 YOLO 模型中的一种。从现有的 YOLO 对象检测模型的数量来看,如何选择最佳模型是一个艰难的选择。 您可能会发现自己正在考虑: 选择哪种 YOLO 模型以获得最佳 FPS? CPU 与 GPU 的推理速度如何?选择哪种 GPU?微型、小型、…...

如何增加网站权重?有效提高网站权重的技巧方法
权重对于网站优化来说非常的重要,那什么是网站权重呢?网站权重是指搜索引擎给网站(包括网页)赋予一定的权威值,对网站(含网页)权威的评估评价。一个网站权重越高,在搜索引擎所占的份…...
)
路径规划 | 图解快速随机扩展树RRT算法(附ROS C++/Python/Matlab仿真)
目录 0 专栏介绍1 什么是RRT算法?2 图解RRT算法原理3 算法仿真与实现3.1 ROS C++实现3.2 Python实现3.3 Matlab实现0 专栏介绍 🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等);局部规划(DWA、APF等);…...
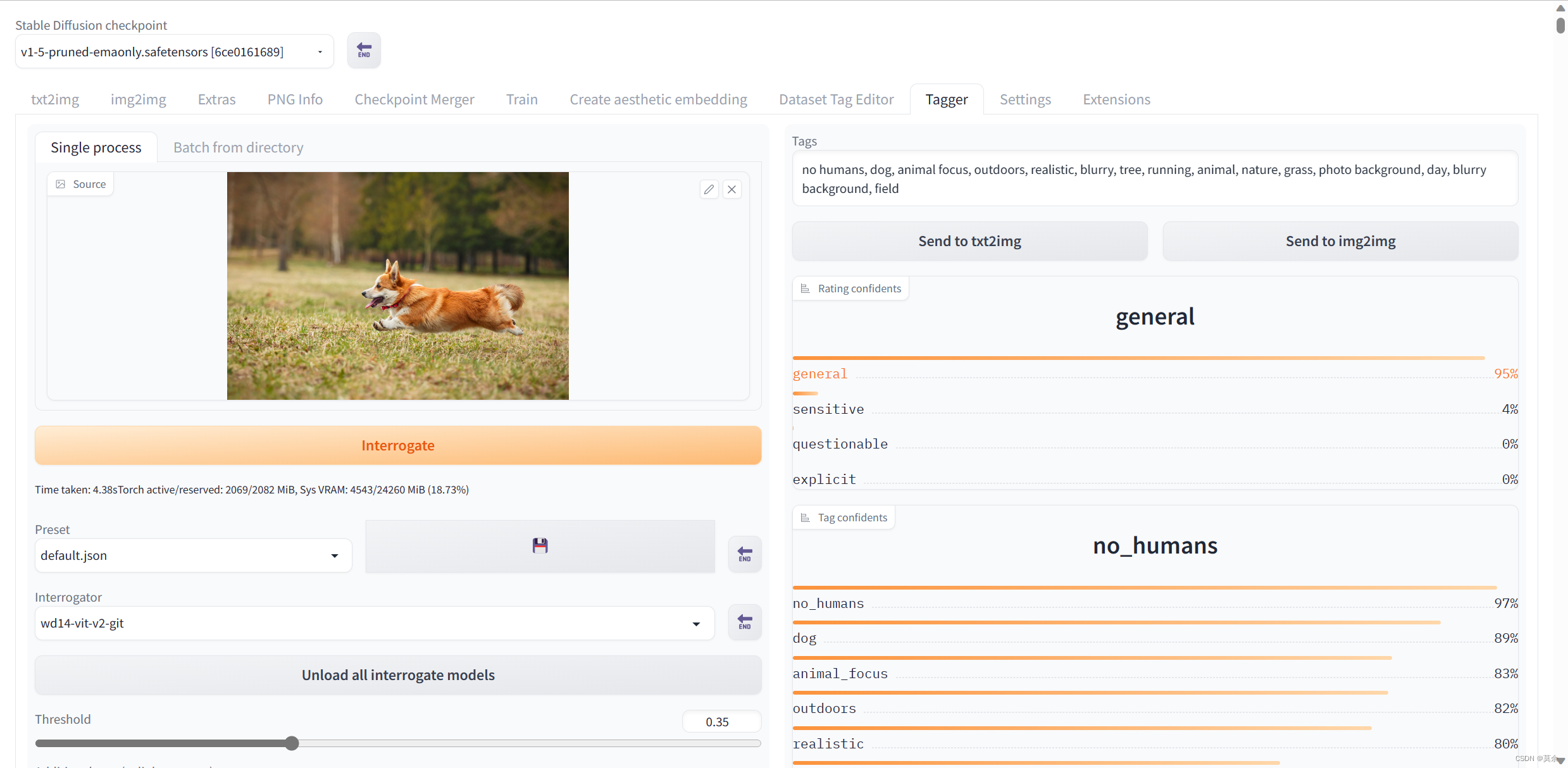
【Stable Diffusion WebUI】一篇文章教你如何安装和使用Stable Diffusion WebUI
文章目录 Stable Diffusion WebUI1. 安装1.1 下载 stable-diffusion-webui1.2 运行 webui.sh 2. 安装插件2.1 命令行安装2.2 extensions 安装2.3 常用插件 3. 使用教程3.1 页面布局3.3 快捷栏设置3.3.1 PNG Info3.3.2 Tagger Stable Diffusion WebUI 1. 安装 1.1 下载 stable…...
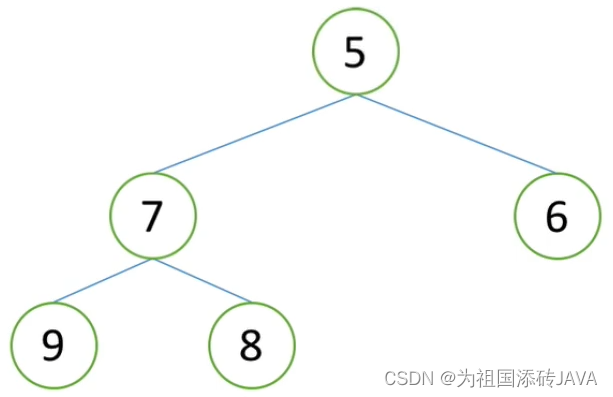
Python篇——数据结构与算法(第二部分)
目录 二、排序算法(承接第一部分) 1、堆排序算法——树的基础知识补充 2、树的基本概念 3、二叉树基础知识 (1)满二叉树 (2)完全二叉树 (3)二叉树的存储方式(表示方式…...

人工智能之读懂CNN卷积神经网络
通过往期文章的分享,我们了解了神经网络的结构,一般分为输入层,隐藏层,输出层 TensorFlow神经网络 那什么是卷积神经网络那,这就要我们追溯一下人类识别图像的原理 人类的视觉原理如下:从原始信号摄入开始(瞳孔摄入像素 Pixels),接着做初步处理(大脑皮层某些细胞发现…...
之协议说明)
go手写Redis(1)之协议说明
手写Redis 参考大佬的go实现redis,自己实现一个简单版本的用于学习go以及网络编程相关 https://github.com/HDT3213/godis https://coding.imooc.com/class/576.html #慕课网课程 源码地址: https://gitee.com/haijun1998/go_redis RESP协议 Redis Ser…...
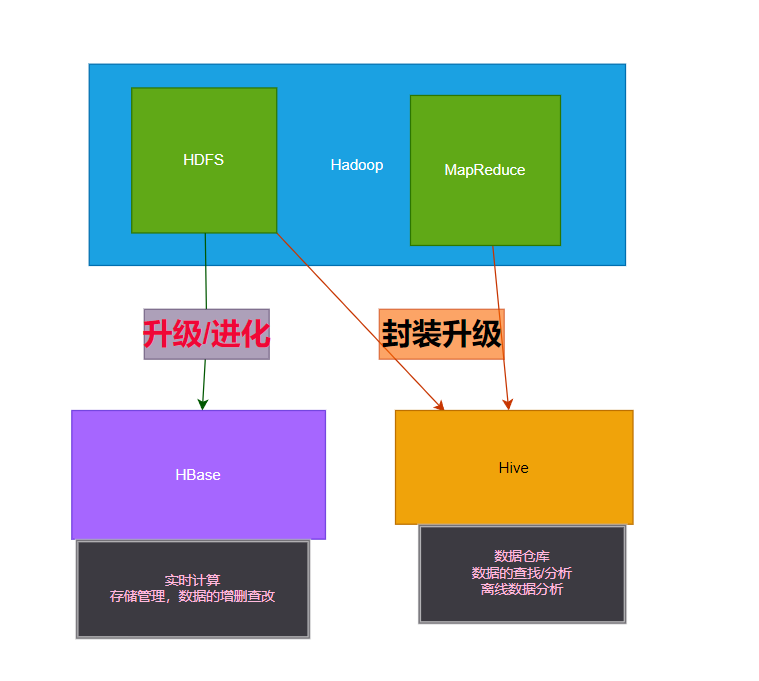
Hadoop/HbBase/Hive/HDFS/MapReduce都是什么?
目录 一图胜万言!! 解释说明 1. hadoop 2. hive 3. hbase 总结 一图胜万言!! 解释说明 1. hadoop 它是一个分布式计算分布式文件系统,前者其实就是 MapReduce,后者是 HDFS 。后者可以独立运行&…...

羽毛球中级提高班课后总结
2023.3.28第一课 🏸️四点对角线步伐练习🏸️ 1️⃣每一次接球一定要有启动步,脚跟离地; 2️⃣两边上网都是先迈右腿,加一个并步,最后一步大迈步,脚跟先落地; 3️⃣右边上网脚尖朝…...

多维时序预测 | Matlab基于最小二乘支持向量机LSSVM多维时间序列预测,LSSVM多变量时间序列预测
文章目录 效果一览文章概述部分源码参考资料效果一览 文章概述 基于最小二乘支持向量机LSSVM多维时间序列预测LSSVM多变量时间序列预测,matlab代码 评价指标包括:MAPE、MAE、RMSE和R2等,代码质量极高,...

KDZK-F水轮发电机转子测试仪
一、产品概述 KDZK-F水轮发电机转子测试仪是判断发电机转子绕组有无匝间短路的专用仪器,可以自动、手动(单向或双向)测量转子绕组的电压、电流、阻抗、功率、相位角等参数。 二、功能与特点 旋转鼠标,操作更方便。 可选择快速的…...
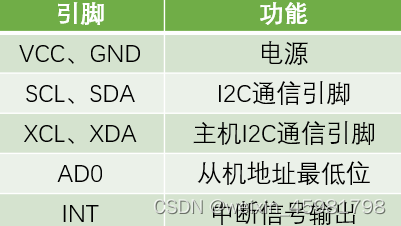
I2C通信协议原理和MPU6050
一、串口通讯 只能在两个设备之间进行 若要三台设备两两通信,则每个设备得需要两组窗口,为3组相互独立的窗口通讯 为解决这个问题:设计了总线通讯,有多种,I2C为其中一种 二、I2C通信 (1&#…...

3.5 RDD持久化机制
一、RDD持久化 1、不采用持久化操作 查看要操作的HDFS文件 以集群模式启动Spark Shell 按照图示进行操作,得RDD4和RDD5 查看RDD4内容,会从RDD1到RDD2到RDD3到RDD4跑一趟 显示RDD5内容,也会从RDD1到RDD2到RDD3到RDD5跑一趟 2、采用持久化…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...
