【C++】 排列与组合算法详解(进阶篇)

文章目录
- 写在前面
- 算法1:朴素算法
- 思路
- 缺点
- 算法2:递推预处理
- 算法3:阶乘逆元
- 算法4:Lucas 定理
写在前面
我上次发了一篇题解:C++排列与组合算法详解
最开始,我是抱着水题解的想法写的,但却成为了阅读量 最高 的文章,没有之一。
所以今天咱们来重制一篇文章,介绍几个进阶优化版的算法。
算法1:朴素算法
思路
具体见 C++排列与组合算法详解
缺点
不能将结果取模,因为朴素的组合公式在取模意义下没用。
算法2:递推预处理
思路
我们发现:
C a 0 = 1 C a b = C a − 1 b + C a − 1 b − 1 ( a , b > 0 ) C_a^0 = 1\\ C_a^b=C_{a-1}^b+C_{a-1}^{b-1}(a,b>0) Ca0=1Cab=Ca−1b+Ca−1b−1(a,b>0)
所以我们可以写一个递推函数(部分非主要内容已省略):
void init_C()
{for (int i = 0; i < N; i ++ ) // N 表示预处理最大的下标for (int j = 0; j <= i; j ++ )if (!j) c[i][j] = 1;else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % P;
}
再预处理阶乘:
void f(int n)
{f[0] = 1;for (int i = 1; i <= n; i ++ )f[i] = (LL)f[i - 1] * i % P;
}
需要排列的话还可以预处理排列:
void init_A(int n)
{for (int i = 0; i <= n; i ++ )for (int j = 0; j <= i; j ++ )a[i][j] = (LL)f[i - j] * c[i][j] % P;
}
时间复杂度: O ( n 2 ) O(n^2) O(n2)
可以处理 5000 5000 5000 以内规模的数据
算法3:阶乘逆元
思路
根据费马小定理可得,当 p p p 为质数时, a p − 1 ≡ 1 ( m o d p ) a^{p-1} \equiv 1\pmod p ap−1≡1(modp)
∴ a p − 2 ≡ 1 a ( m o d p ) \therefore a^{p-2} \equiv \frac{1}{a}\pmod p ∴ap−2≡a1(modp)
这就是乘法逆元,通常使用在需要除法取模的情况。
这里再次提一下排列、组合公式: C a b = a ! b ! ( a − b ) ! , A a b = a ! b ! C_a^b=\frac{a!}{b!(a-b)!},\ \ A_a^b=\frac{a!}{b!} Cab=b!(a−b)!a!, Aab=b!a!
求逆元需要用到快速幂:
LL qpow(LL a, LL b, LL p)
{LL res = 1;while (b){if (b & 1) res = res * a % p;b >>= 1;a = a * a % p;}return res;
}
然后预处理阶乘和阶乘逆元:
f[0] = uf[0] = 1;
for (int i = 1; i < N; i ++ )
{f[i] = (LL)f[i - 1] * i % mod;uf[i] = (LL)uf[i - 1] * qpow(i, mod - 2, mod) % mod;
}
同样的,如果输出排列、组合结果的话需要利用公式。
时间复杂度: O ( n log n ) O(n \log n) O(nlogn)
可以处理 1 0 5 10^5 105 以内规模的数据
思考:读者也可以尝试写 O ( n ) O(n) O(n) 预处理阶乘逆元。
算法4:Lucas 定理
思路
由 Lucas 定理可得:当 p p p 为质数时,
C a b = C a p b p × C a m o d p b m o d p \large{C_a^b=C_{\frac{a}{p}}^{\frac{b}{p}} \times C_{a \bmod p}^{b \bmod p}} Cab=Cpapb×Camodpbmodp
因此,我们可以写一个递归函数 LL lucas(int a, int b),递归出口是 a k < p , b k < p a_k<p, b_k<p ak<p,bk<p 。
递归的过程相当于自上向下将 C a 1 b 1 , C a 2 b 2 , … , C a k b k C_{a_1}^{b_1},C_{a_2}^{b_2},…,C_{a_k}^{b_k} Ca1b1,Ca2b2,…,Cakbk 添加到乘式里。
LL lucas(LL a, LL b)
{if (a < p && b < p) return C(a, b);return (LL)C(a % p, b % p) * lucas(a / p, b / p) % p;
}
这里面的 C(a, b) 是指 算法3 ,即用阶乘和阶乘逆元求组合数。
LL qpow(LL a, LL b, LL p)
{int res = 1;while (b){if (b & 1) res = res * a % p;b >>= 1;a = a * a % p;}return res;
}LL C(LL a, LL b)
{LL res = 1;for (int i = 1, j = a; i <= b; i ++ , j -- ){res = (LL)res * j % p;res = (LL) res * qpow(i, p - 2, p) % p;}return res;
}
同样的,如果输出排列、组合结果的话需要利用公式。
时间复杂度: O ( p × log p n ) O(p \times \log_p n) O(p×logpn)
可以处理 a , b ≤ 1 0 18 , p ≤ 1 0 5 a,b \le 10^{18},p \le 10^5 a,b≤1018,p≤105 以内规模的数据

最后,如果觉得对您有帮助的话,点个赞再走吧!
相关文章:

【C++】 排列与组合算法详解(进阶篇)
文章目录 写在前面算法1:朴素算法思路缺点 算法2:递推预处理思路时间复杂度: O ( n 2 ) O(n^2) O(n2) 算法3:阶乘逆元思路时间复杂度: O ( n log n ) O(n \log n) O(nlogn)思考:读者也可以尝试写 O ( n…...

Godot引擎 4.0 文档 - 循序渐进教程 - 监听玩家输入
本文为Google Translate英译中结果,DrGraph在此基础上加了一些校正。英文原版页面: Listening to player input — Godot Engine (stable) documentation in English 监听玩家输入 在上一课创建您的第一个脚本的基础上,让我们看看任何游戏…...
Docker笔记9 | Docker中网络功能知识梳理和了解
9 | Docker中网络功能知识梳理和了解 1 外部访问容器1.1 访问方式1.2 映射所有接口地址1.3 映射到指定地址的指定端口1.4 映射到指定地址的任意端口1.5 查看映射端口配置 2 容器互联2.1 新建网络2.2 连接容器 3 配置DNS 简单说:Docker 允许通过外部访问容器或容器互…...

生态系统模型:SolVES、DNDC、CMIP6、GEE林业、APSIM、InVEST、无人机遥感、ArcGIS Pro模型等
基于R语言APSIM模型高级应用及批量模拟实践技术 CMIP6 数据处理方法与典型案例分析实践技术 Python 与 Noah-MP 陆面过程模型融合技术及在站点、区域模拟实践应用 双碳目标下基于“遥感”融合技术在碳储量、碳收支、碳循环等多领域监测与模拟实践应用 基于Citespace和vosvi…...
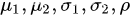
常见分布函数。
一维常见分布函数 1.离散型 ① 0 - 1分布 记 X~B(1,p) 如果X的概率分布为 ( 1 0 p 1 − p ) \begin{pmatrix} 1 & 0 \\ p & 1-p \end{pmatrix} (1p01−p),则称X服从参数为P的0-1分布(0<p<1)。 注:0-1分布又称一次伯努利试…...
【网络安全】红队攻防之基础免杀
引言 本文主要介绍“反射型 dll 注入”及“柔性加载”技术。 反射型 dll 注入 为什么需要反射型 dll 注入 常规的 dll 注入代码如下: int main(int argc, char *argv[]) {HANDLE processHandle;PVOID remoteBuffer;wchar_t dllPath[] TEXT("C:\\experimen…...
CTF入门指南
何为CTF ? CTF(Capture The Flag)夺旗比赛,在网络安全领域中指的是网络安全技术人员之间进行技术竞技的一种比赛形式。CTF起源于1996年DEFCON全球黑客大会,以代替之前黑客们通过互相发起真实攻击进行技术比拼的方式。…...
)
C:入门级积累(4)
(int *)malloc(10 * sizeof(int))memory allocate动态分配内存,malloc的出现时为了弥补静态内存分配的缺点,传统数组的长度一旦定义之后,就不能更改,比如说,如果我有一个业务在这之前给分配的大小为100,但是࿰…...
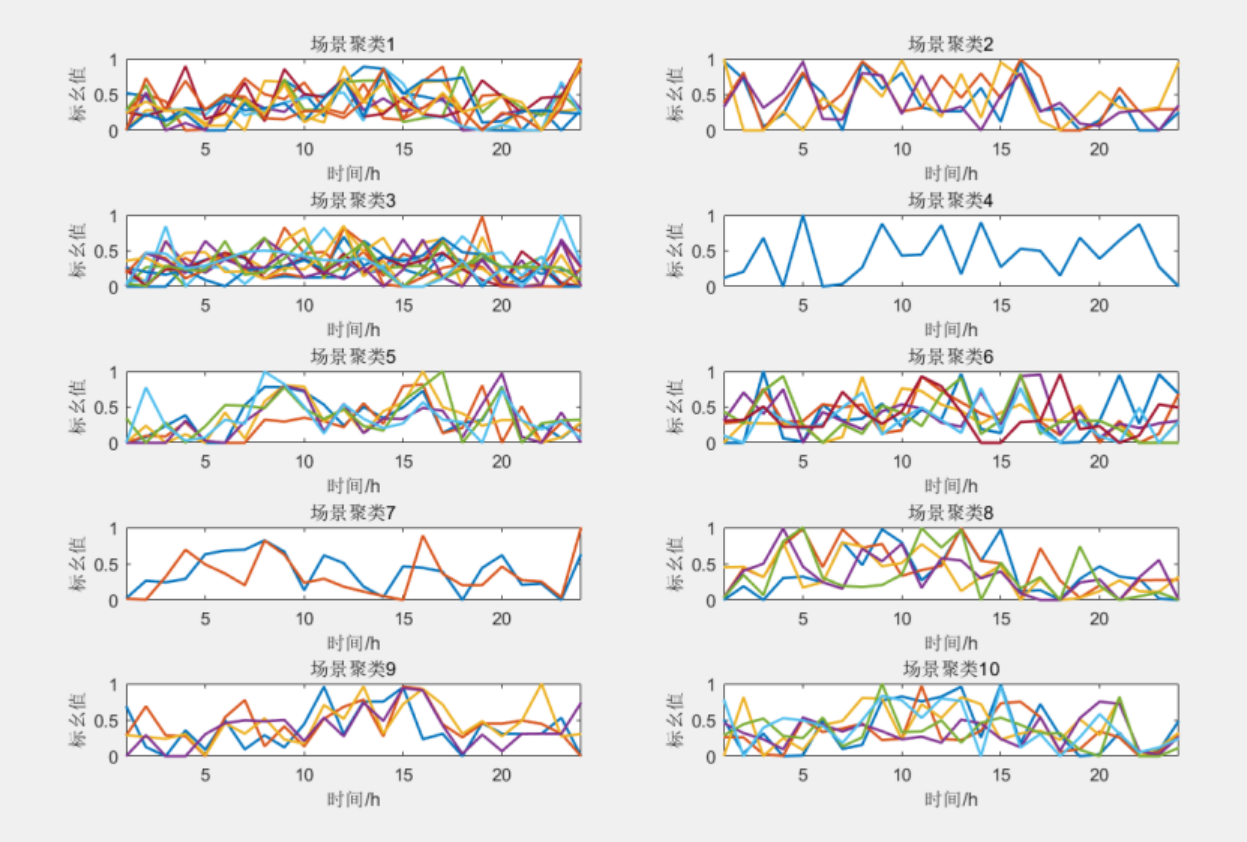
基于DBSCAN密度聚类的风电-负荷场景削减方法
目录 1 主要内容 基于密度聚类的数据预处理: 场景提取: 算法流程: 2 部分程序 3 程序结果 4 下载链接 1 主要内容 该程序复现文章《氢能支撑的风-燃气耦合低碳微网容量优化配置研究》第三章内容,实现的是基于DBSCAN…...

服务(第二十七篇)squid-传统、穿透、反向代理
squid代理服务器: 主要提供缓存加速、应用层过滤控制的功能。 代理的工作机制: 1、代替客户机向网站请求数据,从而可以隐藏用户的真实IP地址。 2、将获得的网页数据(静态 Web 元素)保存到缓存中并发送给客户机&#x…...

golang yaml 解析问题
golang 中解析 yaml 格式内容可以使用 yaml.v3 库来解决。下载 go 依赖 go get -u gopkg.in/yaml.v31. 示例 yaml 数据 config_mail_template:description: 验证码one: Verification Codeother: Verification Codeconfig_mail_template_reset_code:description: 重置密码one:…...
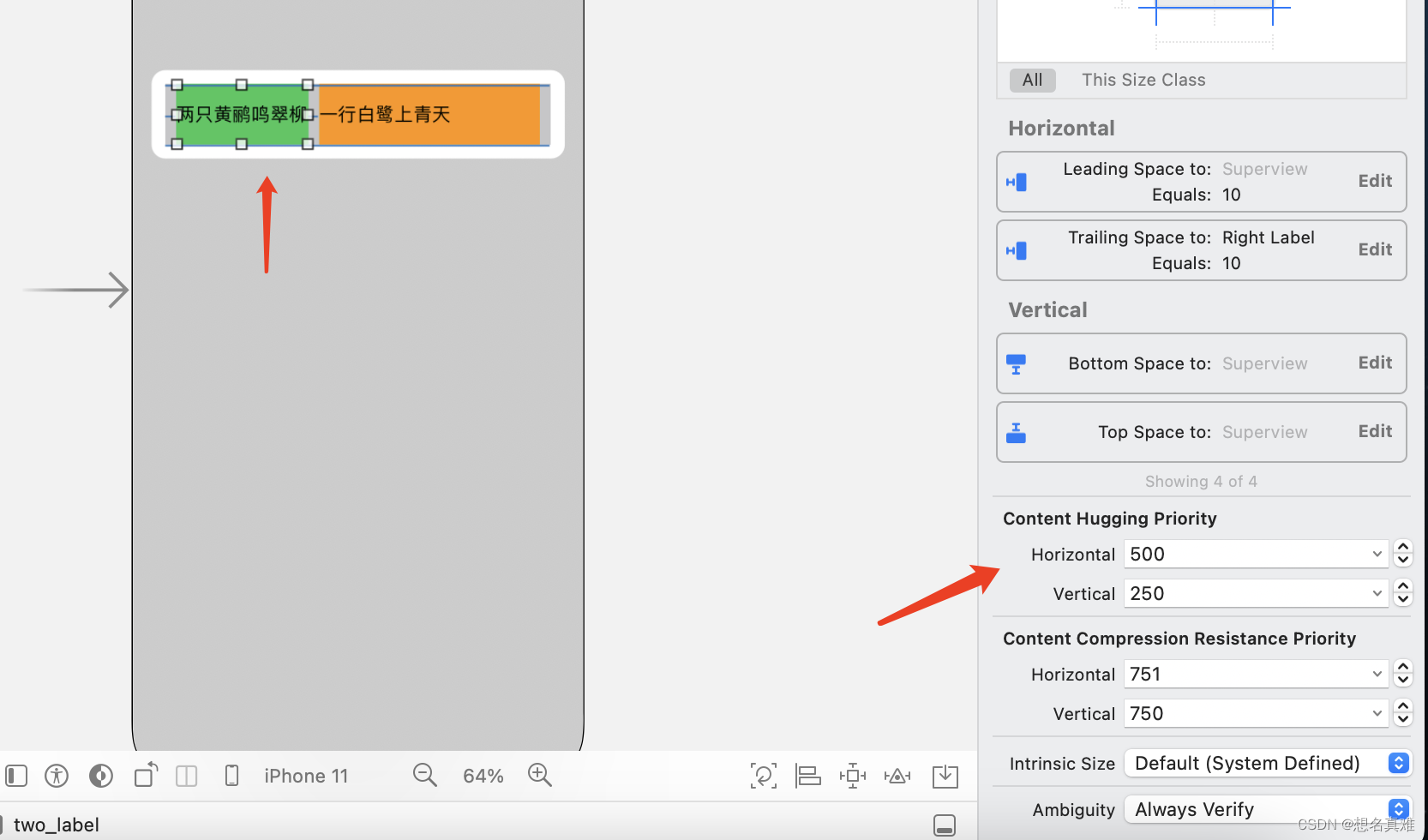
setContentHuggingPriority和setContentCompressionResistancePriority的使用
需求: 两个label并排显示,文字内容由服务器返回,label宽度以文字内容自适应,label之间间距大于等于10. 需要考虑以下情况: 当两个label的宽度和 < 屏幕宽度时,各自设置约束,无需处理&#…...

java springboot yml文件配置 多环境yml
如果是properties改用yml,直接改后缀,原文件中的配置语法改用yml的语法即可,系统会自动扫描application.properties和application.yml文件(注意:改了之后需要maven 命令 clean一下,清个缓存)。 …...
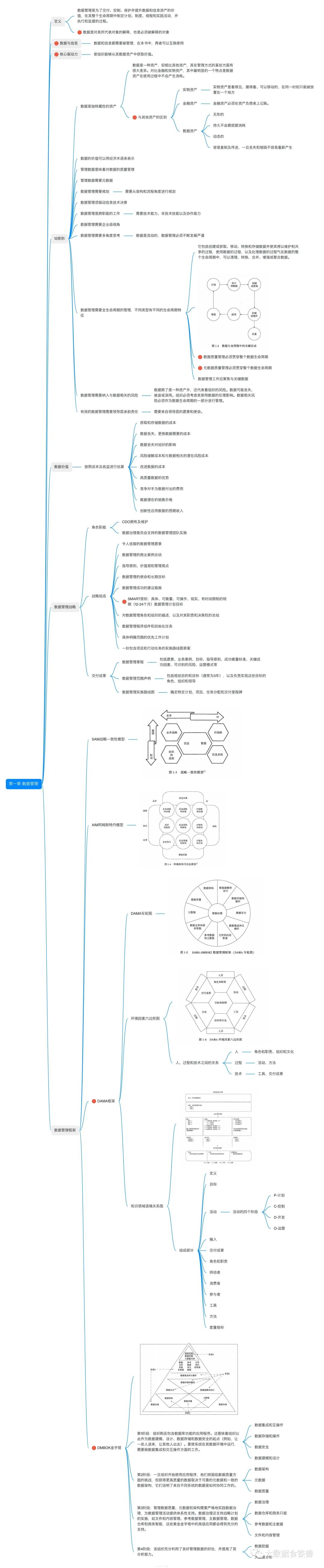
DMBOK知识梳理for CDGA/CDGP——第一章数据管理(附常考知识点)
第一章 数据管理 第一章在 CDGA|CDGP考试中分值占比均不是很高,主要侧重点是考概念性的知识,理解数据管理的目标原则、还有与其他概念的区别点,同时掌握几个关键核心的图(车轮图、六边形图、语境关系图)。总体来说难度…...
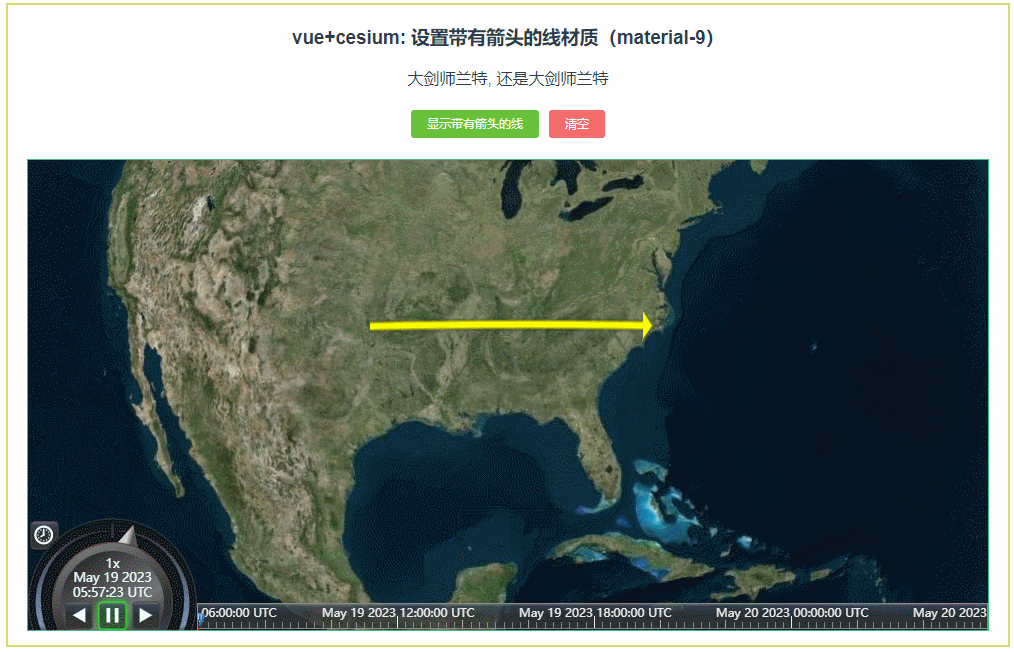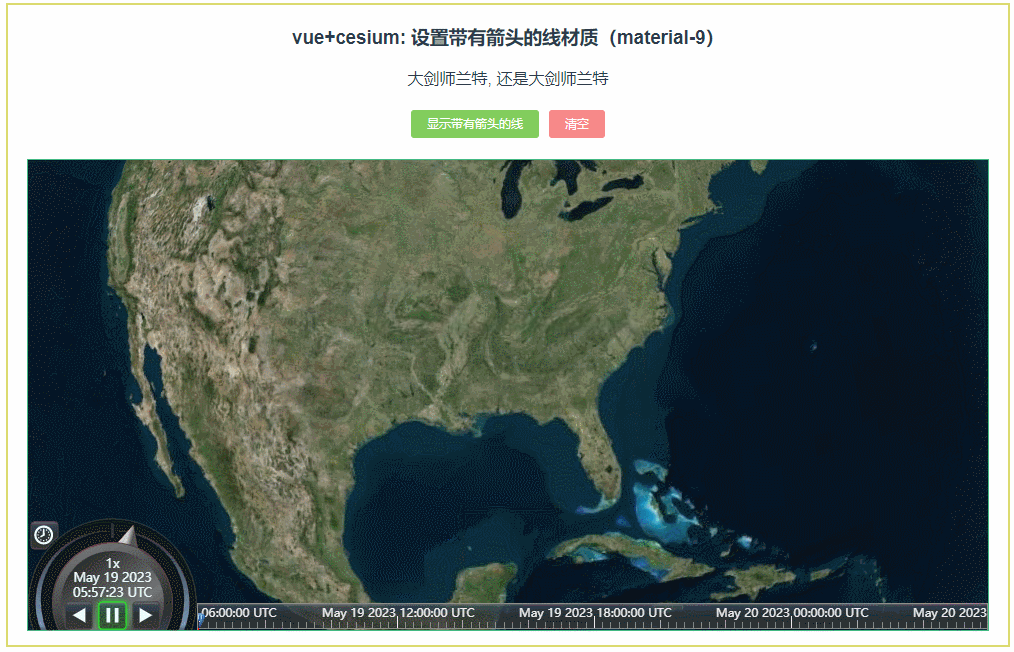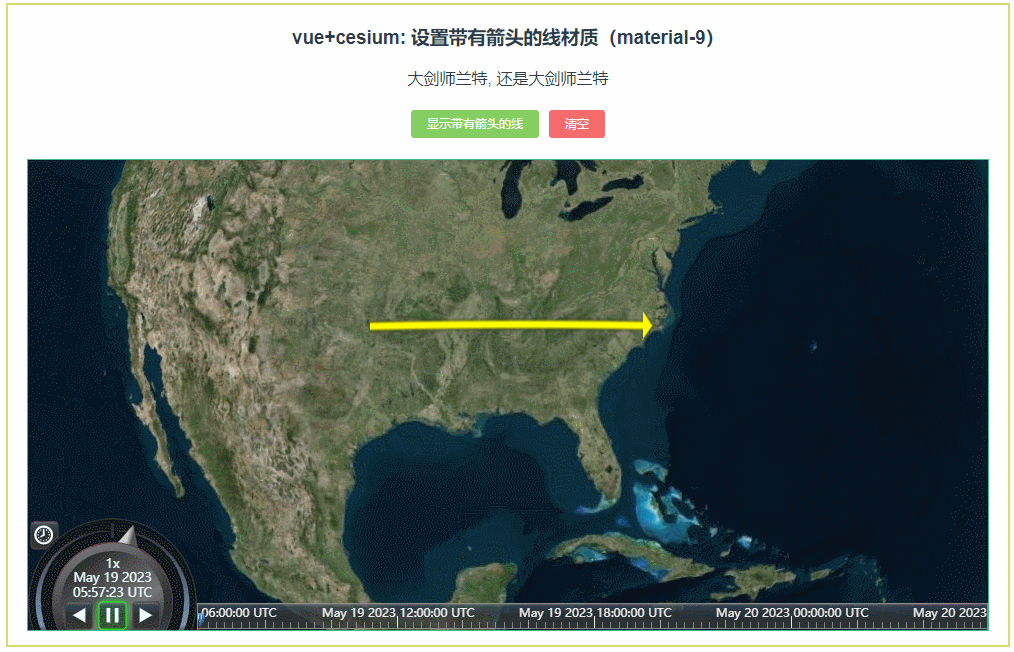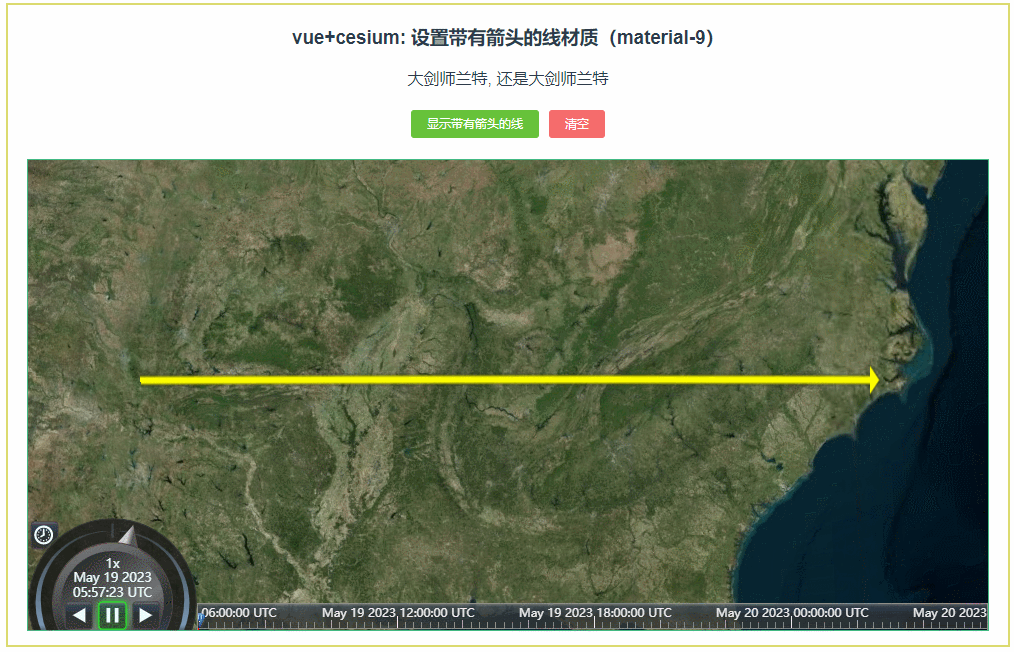
065:cesium设置带有箭头的线材质(material-9)
第065个 点击查看专栏目录 本示例的目的是介绍如何在vue+cesium中设置带有箭头的线材质,请参考源代码,了解PolylineArrowMaterialProperty的应用。 直接复制下面的 vue+cesium源代码,操作2分钟即可运行实现效果. 文章目录 示例效果配置方式示例源代码(共82行)相关API参考…...

Java常用API
1 常用API API(:Application Programming Interface ):应用程序编程接口1.1 Math类 Math中没有构造方法,类的成员都是静态的(static修饰),通过类名就可以直接调用常用方法方法名说明public static int abs(int a)获取参数a的绝对值public static double ceil(double a) …...

【C++ 学习 ⑥】- C++ 动态内存管理详解
目录 一、new 表达式和 delete 表达式的工作机理 二、operator new 和 operator delete 函数 2.1 - 标准库定义 2.2 - 重载 三、定位 new 表达式 四、常见面试题 4.1 - malloc/free 和 new/delete 的区别 4.2 - 内存泄漏 在 C 中,new 和 delete 既是关键字&…...

【5.21】六、自动化测试—常见技术
目录 6.2 自动化测试常见技术 1. 录制与回放测试 2. 脚本测试 3. 数据驱动测试 6.2 自动化测试常见技术 自动化测试技术有很多种,这里介绍3种常见的技术: 1. 录制与回放测试 录制是指使用自动化测试工具对桌面应用程序或者是Web页面的某一项功能进…...

JavaScript中的事件循环机制,包括事件循环的原理、宏任务和微任务、事件队列和调用栈、以及如何优化事件循环
JavaScript中的事件循环机制是JavaScript运行引擎的核心之一,它决定了代码的执行方式和效率。本文将从几个方面介绍JavaScript中的事件循环机制,包括事件循环的原理、宏任务和微任务、事件队列和调用栈、以及如何优化事件循环。 一、事件循环的原理 事…...

【华为OD机试c++】解压报文【2023 B卷 |200分】
题目描述 为了提升数据传输的效率,会对传输的报文进行压缩处理。 输入一个压缩后的报文,请返回它解压后的原始报文。 压缩规则:n[str],表示方括号内部的 str 正好重复 n 次。 注意 n 为正整数(0 < n < 100&a…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
