常见分布函数。
一维常见分布函数
1.离散型
① 0 - 1分布 记 X~B(1,p)
如果X的概率分布为 ( 1 0 p 1 − p ) \begin{pmatrix} 1 & 0 \\ p & 1-p \end{pmatrix} (1p01−p),则称X服从参数为P的0-1分布(0<p<1)。
注:0-1分布又称一次伯努利试验或两点分布。
②二项分布 记 X~B(n,p)
如果X的概率分布为 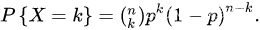 (k=0,1,2,3…n;0<p<1),称X服从参数为(n,p)的二项式分布,又叫N重伯努利试验。
(k=0,1,2,3…n;0<p<1),称X服从参数为(n,p)的二项式分布,又叫N重伯努利试验。
③泊松分布 记 X~P(λ)
如果X的概率分布服从为: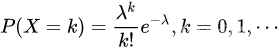 (λ>0).
(λ>0).
则称X服从参数为λ的泊松分布。
表示k个质点来流发生的概率,如某商场8点源源不断往返k人发生的概率。
注:λ是强度,如单位时间内平均来了多少人。
④几何分布 记 X ~ G ( p)
如果X的概率分布为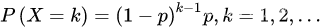
则称X服从参数为p的几何分布。又叫离散型概率分布,无穷伯努利试验。
注1:X表示伯努利试验中事件A首次发生所需要做的试验次数,首中即停止。
注2:几何分布与几何没关系,历史上叫错了。
⑤超几何分布 记 X ~ H(n,N,M)
如果X的概率分布为: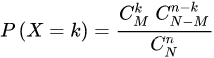 (max{0,n-N+M}<= k <= min{M,n} ; M,N,n为正整数 且 M <= N,n <= N,k为整数).
(max{0,n-N+M}<= k <= min{M,n} ; M,N,n为正整数 且 M <= N,n <= N,k为整数).
2.连续型
①均匀分布 记 X ~ U(a,b)
如果随机变量X的概率密度和分布函数为:
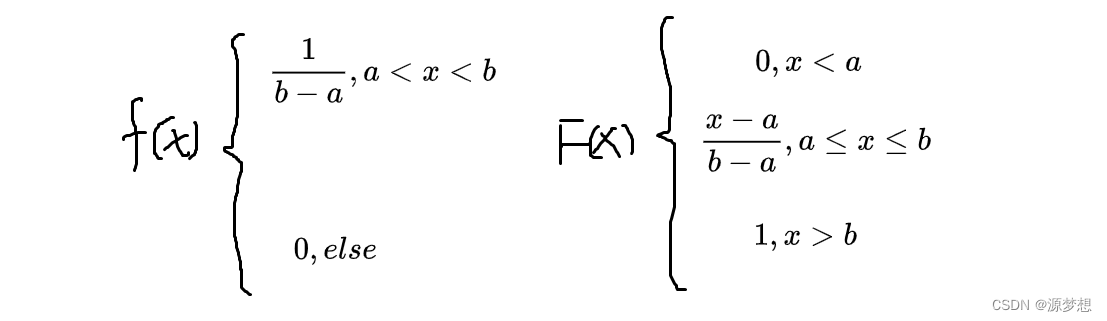
则称X在区间(a,b)上服从均匀分布。
②指数分布 记 X ~ E(λ)
如果随机变量X的概率密度和分布函数为:λ>0
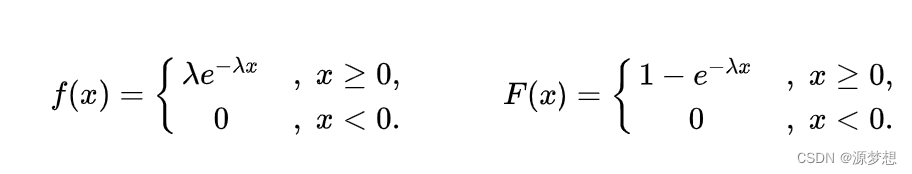
注:这里λ表示失效率。
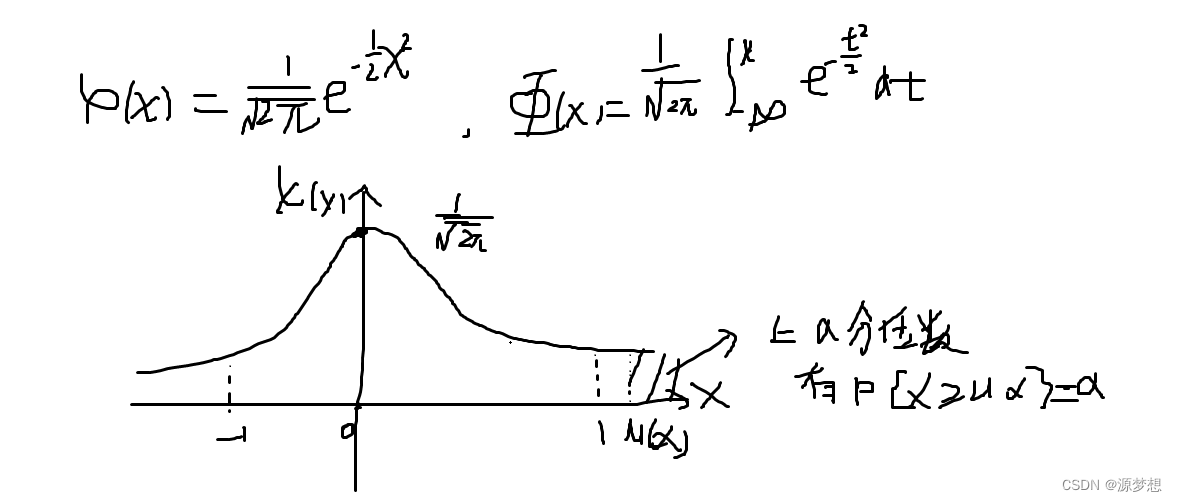
③正态分布 记 X~N(μ,σ2)
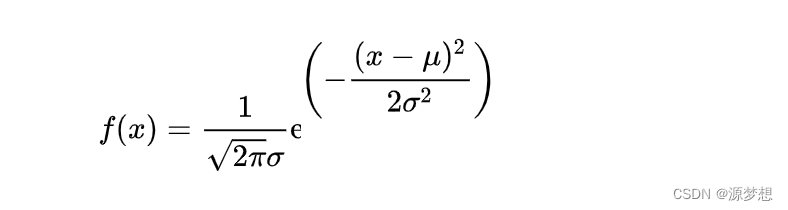
其中 -∞ < μ < +∞, σ > 0, 则称X服从参数为(μ,σ2) 的正态分布或称X为正态变量。
注1:此时f(x)图形关于x = μ 对称,即 f(μ - x) = f(μ + x),并在 x = μ有唯一最大值f(μ)。
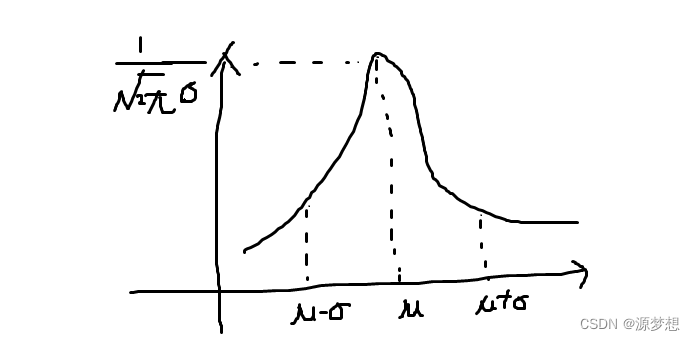
注2:称μ = 0,σ = 1时的正态分布为标准正态分布,通常记为符号φ(x)。其中φ(x)为偶函数,有φ(0) = 1/2,φ(-x) = 1 - φ(x)。
二维常见分布函数
1.连续型
①二维均匀分布
称(X,Y)在平面有界区域D上服从均匀分布,如果(X,Y)的概率密度为:
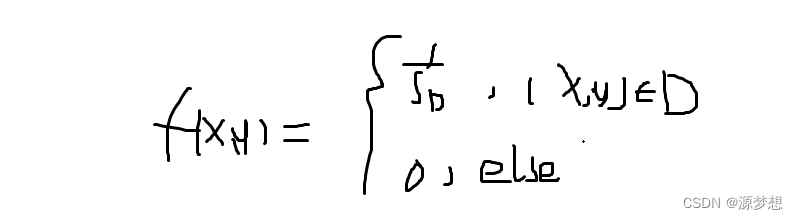
注:将密度均匀撒在区域D上.sD为D面积。
②二维正态分布 记 (X,Y)~(μ1,μ2,σ12,σ22,ρ)
如果(X,Y)的密度函数为: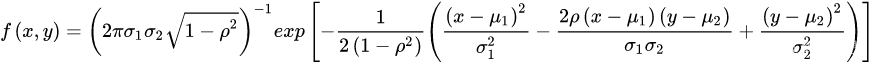
其中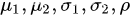 都是常数我们称(X,Y)服从参数为
都是常数我们称(X,Y)服从参数为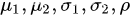 的二维正态分布.
的二维正态分布.
注:ρ为XY的线性相关系数。
相关文章:
常见分布函数。
一维常见分布函数 1.离散型 ① 0 - 1分布 记 X~B(1,p) 如果X的概率分布为 ( 1 0 p 1 − p ) \begin{pmatrix} 1 & 0 \\ p & 1-p \end{pmatrix} (1p01−p),则称X服从参数为P的0-1分布(0<p<1)。 注:0-1分布又称一次伯努利试…...
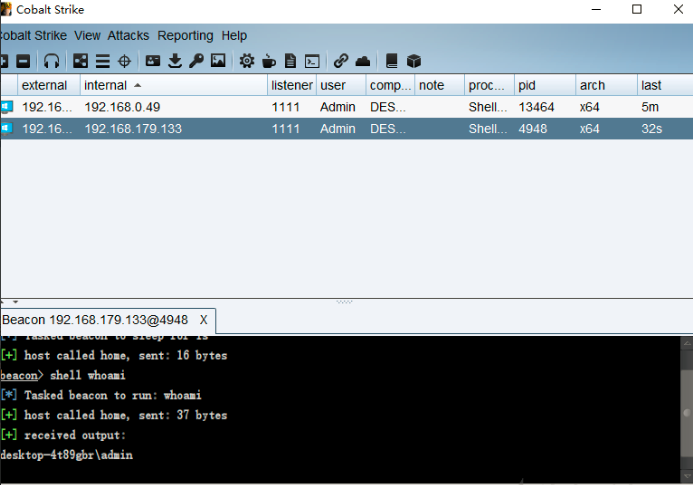
【网络安全】红队攻防之基础免杀
引言 本文主要介绍“反射型 dll 注入”及“柔性加载”技术。 反射型 dll 注入 为什么需要反射型 dll 注入 常规的 dll 注入代码如下: int main(int argc, char *argv[]) {HANDLE processHandle;PVOID remoteBuffer;wchar_t dllPath[] TEXT("C:\\experimen…...
CTF入门指南
何为CTF ? CTF(Capture The Flag)夺旗比赛,在网络安全领域中指的是网络安全技术人员之间进行技术竞技的一种比赛形式。CTF起源于1996年DEFCON全球黑客大会,以代替之前黑客们通过互相发起真实攻击进行技术比拼的方式。…...
)
C:入门级积累(4)
(int *)malloc(10 * sizeof(int))memory allocate动态分配内存,malloc的出现时为了弥补静态内存分配的缺点,传统数组的长度一旦定义之后,就不能更改,比如说,如果我有一个业务在这之前给分配的大小为100,但是࿰…...
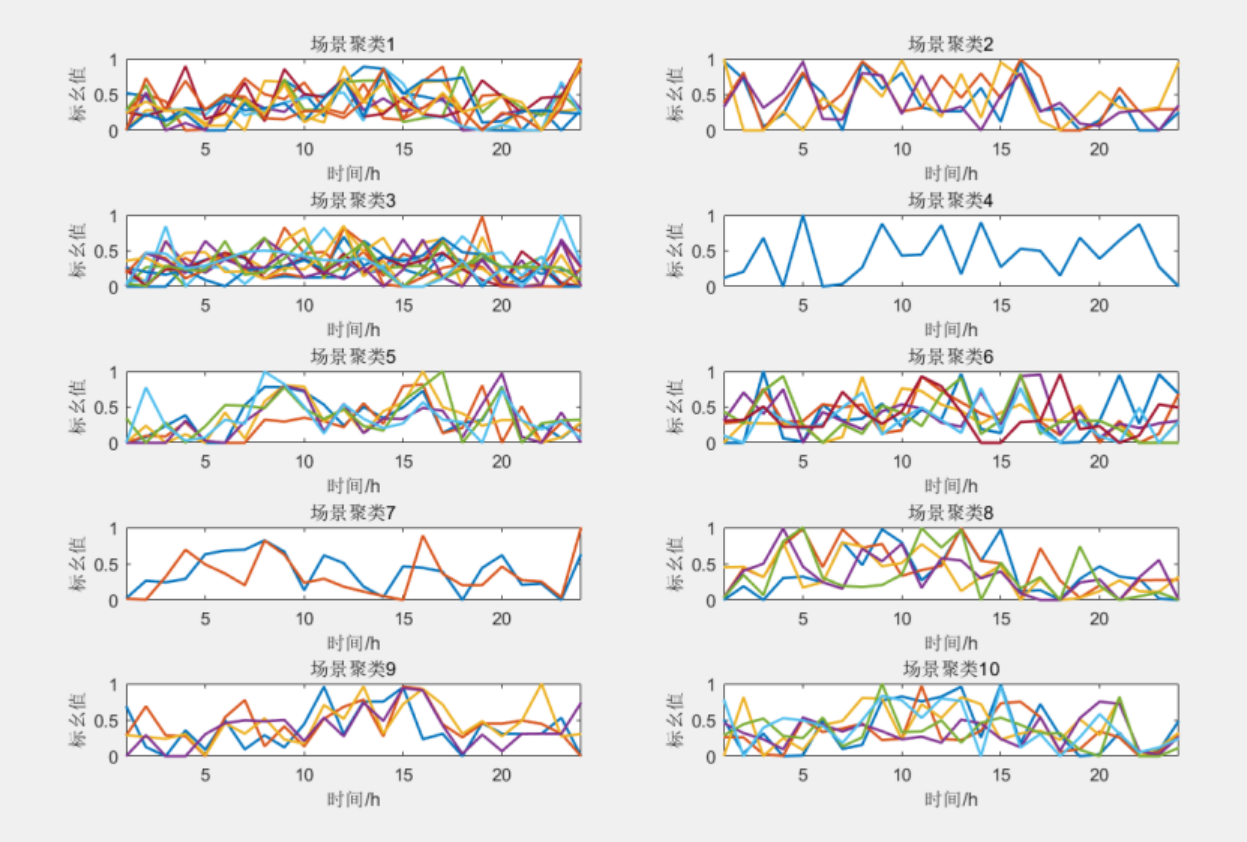
基于DBSCAN密度聚类的风电-负荷场景削减方法
目录 1 主要内容 基于密度聚类的数据预处理: 场景提取: 算法流程: 2 部分程序 3 程序结果 4 下载链接 1 主要内容 该程序复现文章《氢能支撑的风-燃气耦合低碳微网容量优化配置研究》第三章内容,实现的是基于DBSCAN…...

服务(第二十七篇)squid-传统、穿透、反向代理
squid代理服务器: 主要提供缓存加速、应用层过滤控制的功能。 代理的工作机制: 1、代替客户机向网站请求数据,从而可以隐藏用户的真实IP地址。 2、将获得的网页数据(静态 Web 元素)保存到缓存中并发送给客户机&#x…...

golang yaml 解析问题
golang 中解析 yaml 格式内容可以使用 yaml.v3 库来解决。下载 go 依赖 go get -u gopkg.in/yaml.v31. 示例 yaml 数据 config_mail_template:description: 验证码one: Verification Codeother: Verification Codeconfig_mail_template_reset_code:description: 重置密码one:…...
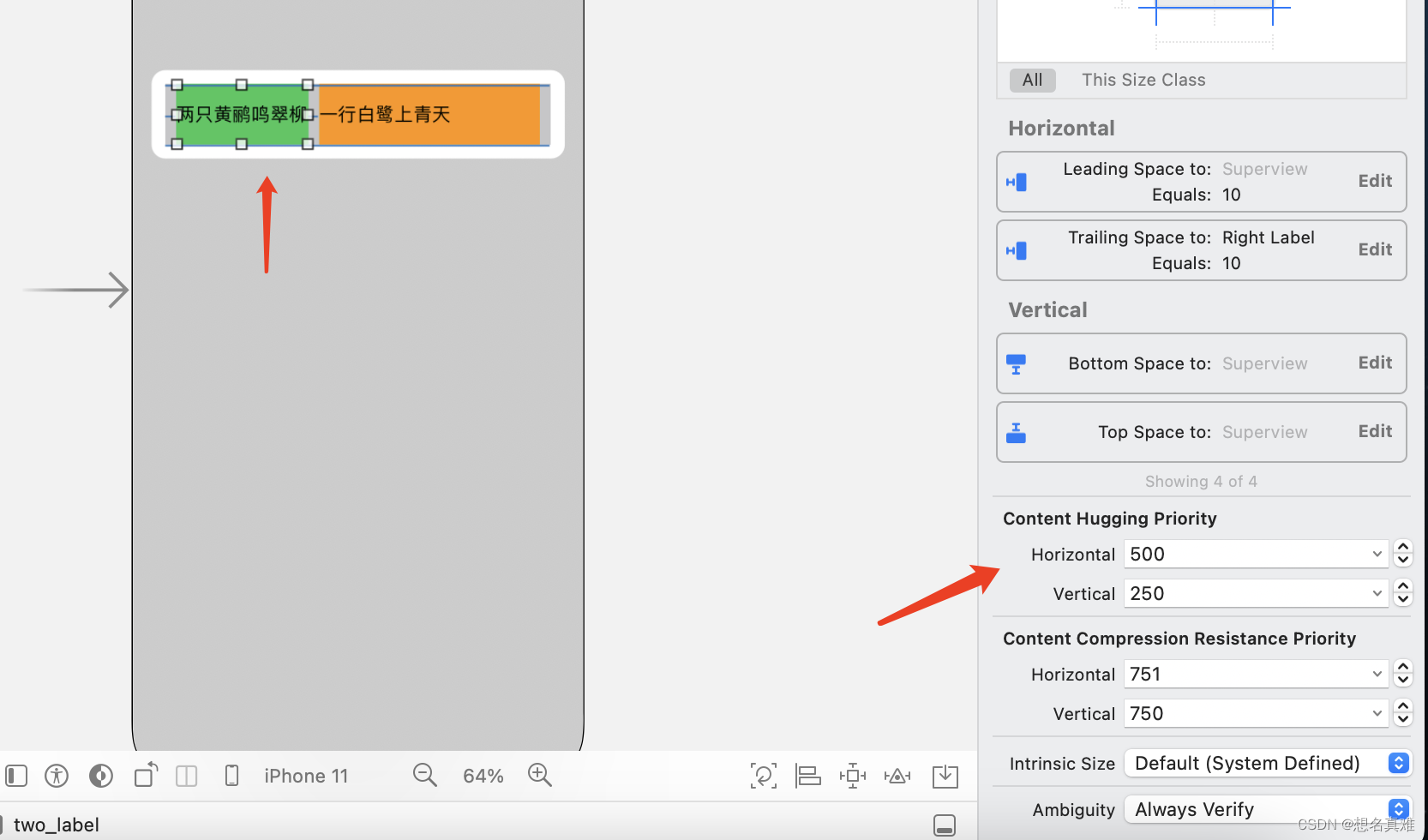
setContentHuggingPriority和setContentCompressionResistancePriority的使用
需求: 两个label并排显示,文字内容由服务器返回,label宽度以文字内容自适应,label之间间距大于等于10. 需要考虑以下情况: 当两个label的宽度和 < 屏幕宽度时,各自设置约束,无需处理&#…...

java springboot yml文件配置 多环境yml
如果是properties改用yml,直接改后缀,原文件中的配置语法改用yml的语法即可,系统会自动扫描application.properties和application.yml文件(注意:改了之后需要maven 命令 clean一下,清个缓存)。 …...
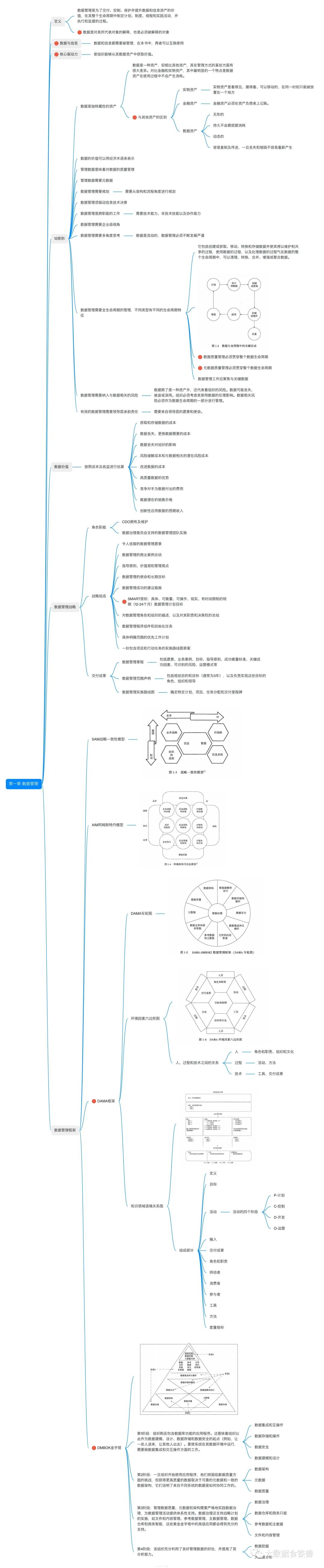
DMBOK知识梳理for CDGA/CDGP——第一章数据管理(附常考知识点)
第一章 数据管理 第一章在 CDGA|CDGP考试中分值占比均不是很高,主要侧重点是考概念性的知识,理解数据管理的目标原则、还有与其他概念的区别点,同时掌握几个关键核心的图(车轮图、六边形图、语境关系图)。总体来说难度…...
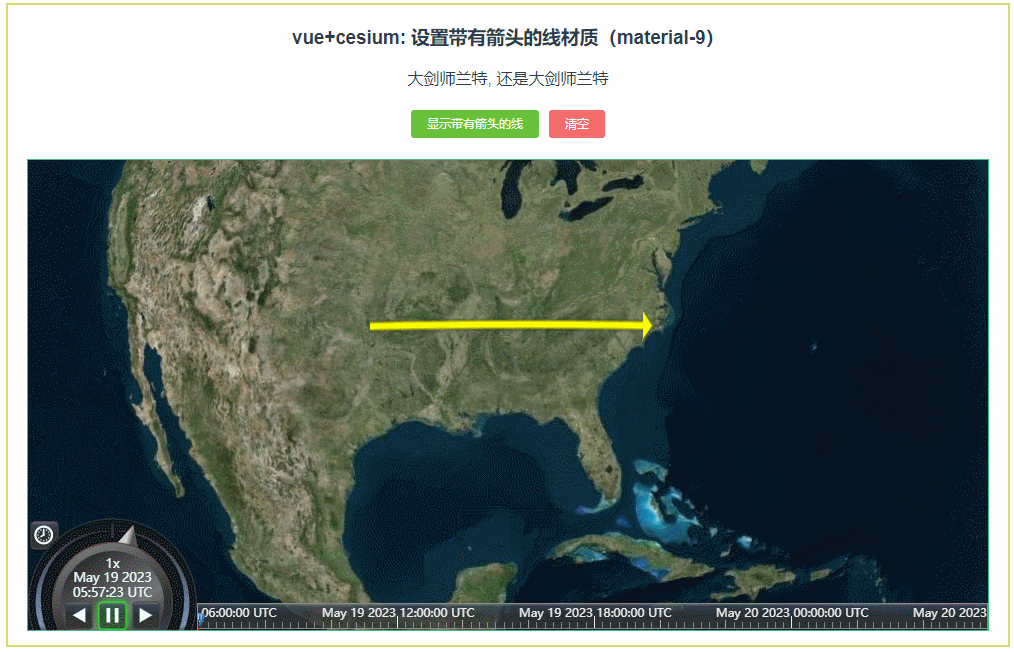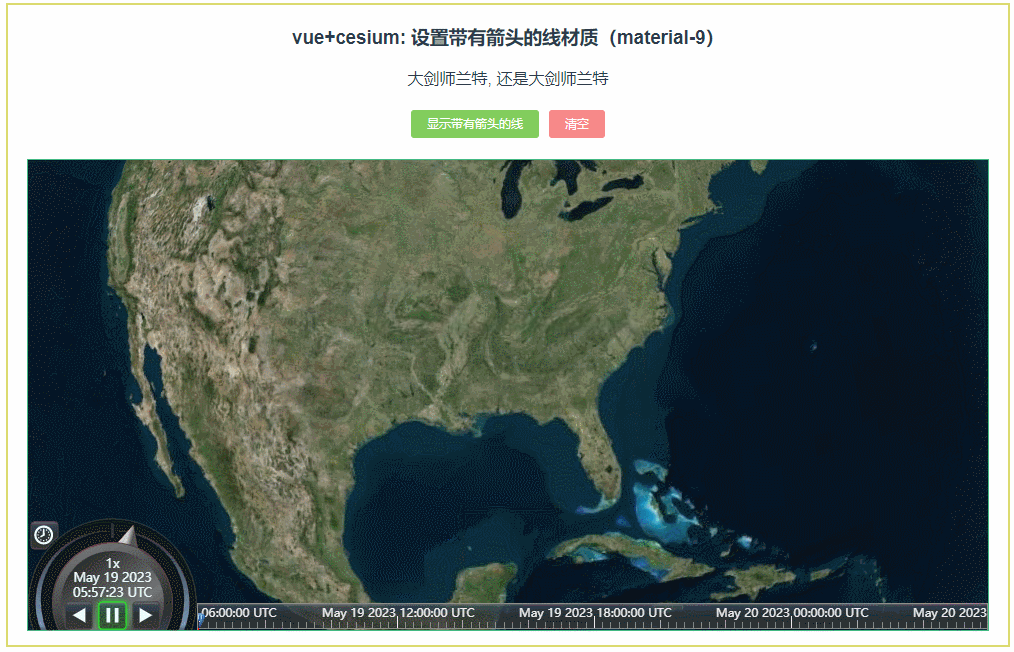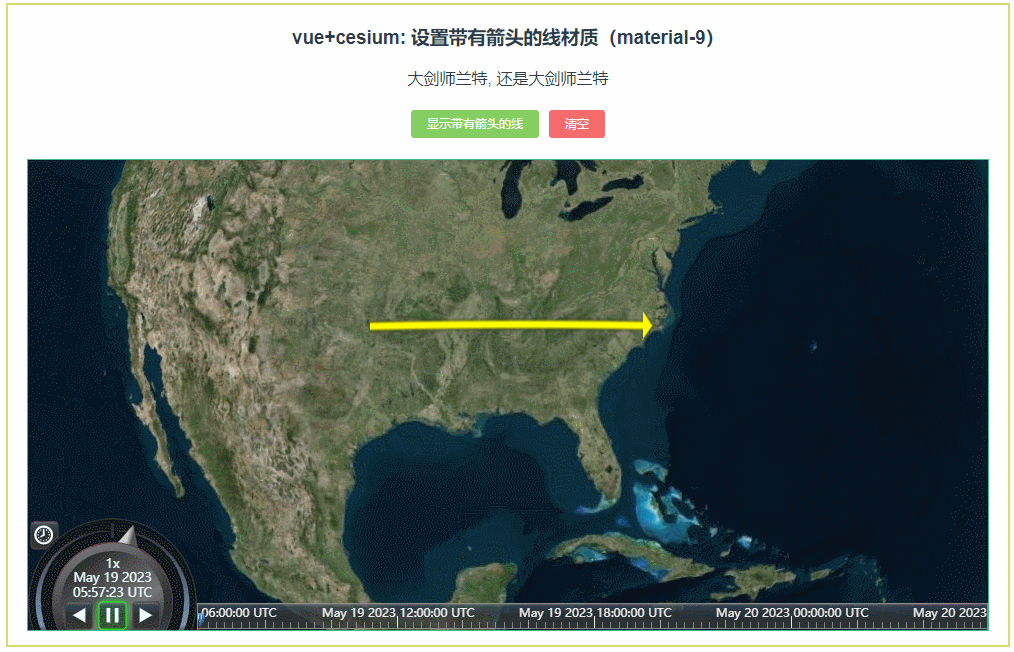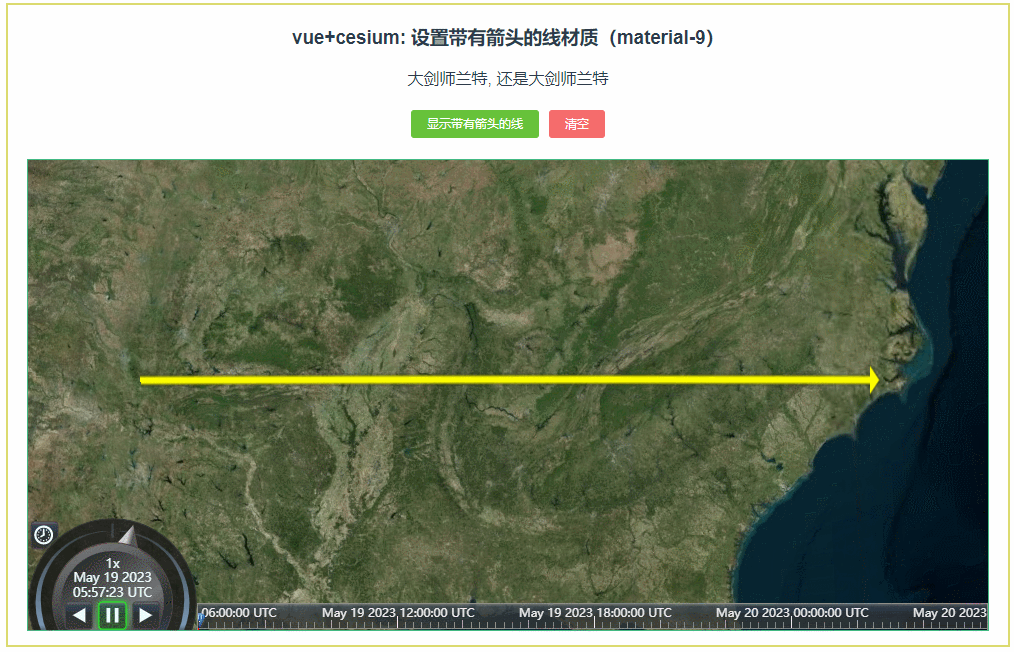
065:cesium设置带有箭头的线材质(material-9)
第065个 点击查看专栏目录 本示例的目的是介绍如何在vue+cesium中设置带有箭头的线材质,请参考源代码,了解PolylineArrowMaterialProperty的应用。 直接复制下面的 vue+cesium源代码,操作2分钟即可运行实现效果. 文章目录 示例效果配置方式示例源代码(共82行)相关API参考…...

Java常用API
1 常用API API(:Application Programming Interface ):应用程序编程接口1.1 Math类 Math中没有构造方法,类的成员都是静态的(static修饰),通过类名就可以直接调用常用方法方法名说明public static int abs(int a)获取参数a的绝对值public static double ceil(double a) …...

【C++ 学习 ⑥】- C++ 动态内存管理详解
目录 一、new 表达式和 delete 表达式的工作机理 二、operator new 和 operator delete 函数 2.1 - 标准库定义 2.2 - 重载 三、定位 new 表达式 四、常见面试题 4.1 - malloc/free 和 new/delete 的区别 4.2 - 内存泄漏 在 C 中,new 和 delete 既是关键字&…...

【5.21】六、自动化测试—常见技术
目录 6.2 自动化测试常见技术 1. 录制与回放测试 2. 脚本测试 3. 数据驱动测试 6.2 自动化测试常见技术 自动化测试技术有很多种,这里介绍3种常见的技术: 1. 录制与回放测试 录制是指使用自动化测试工具对桌面应用程序或者是Web页面的某一项功能进…...

JavaScript中的事件循环机制,包括事件循环的原理、宏任务和微任务、事件队列和调用栈、以及如何优化事件循环
JavaScript中的事件循环机制是JavaScript运行引擎的核心之一,它决定了代码的执行方式和效率。本文将从几个方面介绍JavaScript中的事件循环机制,包括事件循环的原理、宏任务和微任务、事件队列和调用栈、以及如何优化事件循环。 一、事件循环的原理 事…...

【华为OD机试c++】解压报文【2023 B卷 |200分】
题目描述 为了提升数据传输的效率,会对传输的报文进行压缩处理。 输入一个压缩后的报文,请返回它解压后的原始报文。 压缩规则:n[str],表示方括号内部的 str 正好重复 n 次。 注意 n 为正整数(0 < n < 100&a…...

JS中Array的forEach、map、filter方法区别?
一:基本用法 1、forEach()函数用于对数组中的每个元素执行给定的函数,而它不返回任何值,它只是对每个元素调用传入的函数。这个函数可以接受三个参数:当前元素的值、当前元素的索引和整个数组。 const arr [1, 2, 3]; arr.forE…...
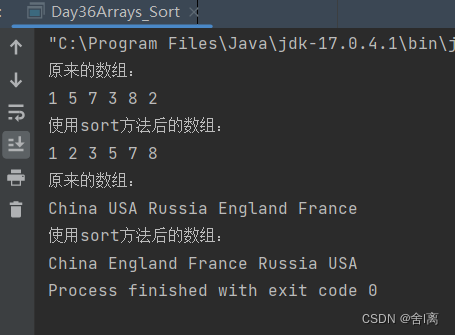
Java的Arrays类的sort()方法(41)
目录 sort()方法 1.sort()方法的格式 2.使用sort()方法时要导入的类 3.作用 4.作用的对象 5.注意 6.代码及结果 (1)代码 (2)结果 sort(&…...

Redis安装及其配置文件修改
一、redis 安装 点击即可下载 https://download.redis.io/releases/ 将下载后的包通过xftp上传到服务器 解压,我这边是解压到/usr/local目录下 -- 创建路径 mkdir /usr/local/redis -- 解压 tar -zxvf redis-4.0.0.tar.gz -C /usr/local/redis 为防止编译失败&am…...
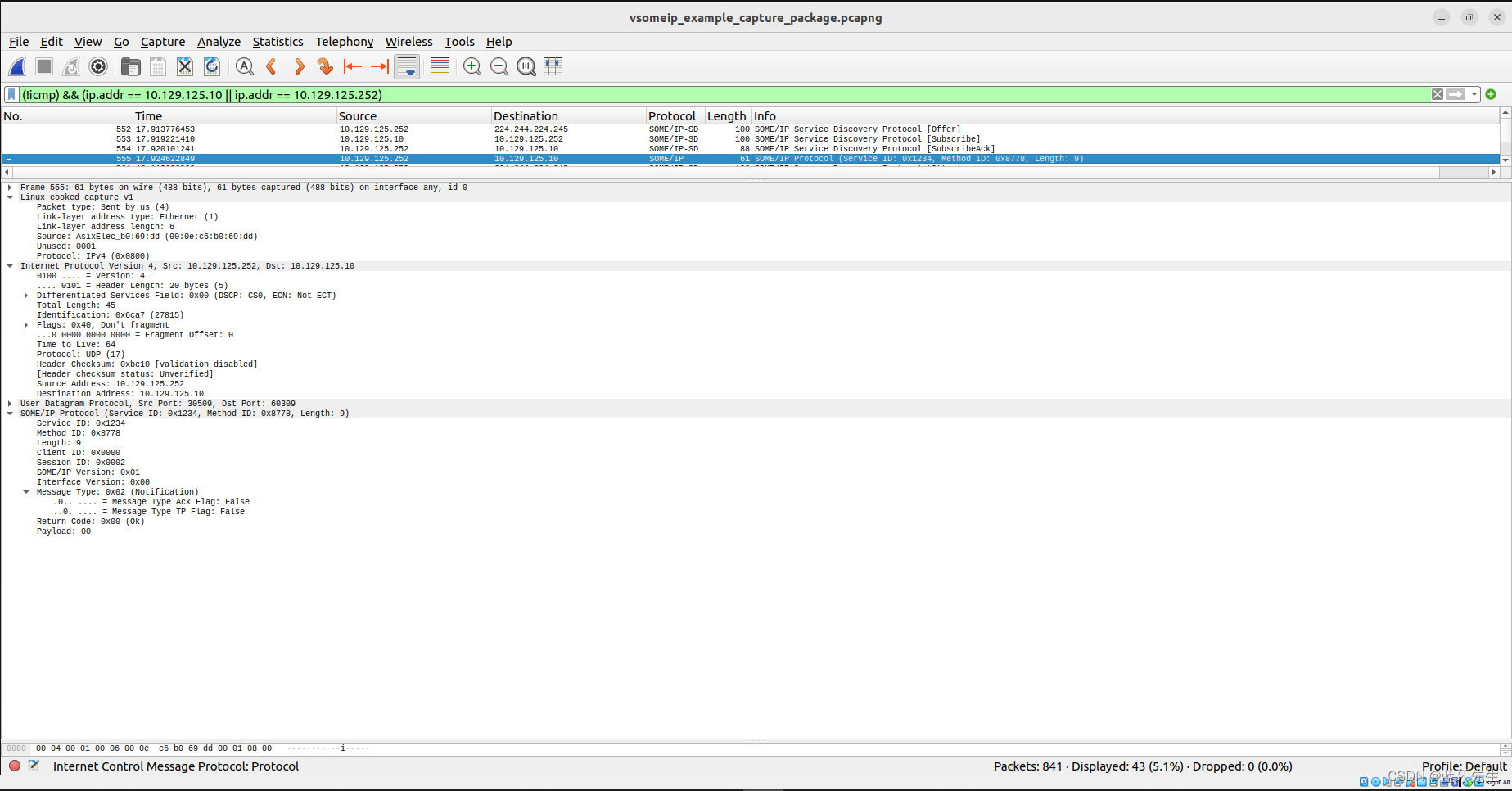
VSOMEIP3抓包数据
环境 $ cat /etc/os-release NAME"Ubuntu" VERSION"20.04.6 LTS (Focal Fossa)" IDubuntu ID_LIKEdebian PRETTY_NAME"Ubuntu 20.04.6 LTS" VERSION_ID"20.04" HOME_URL"https://www.ubuntu.com/" SUPPORT_URL"https:/…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...
