Redis安装及其配置文件修改
一、redis 安装
-
点击即可下载
https://download.redis.io/releases/ -
将下载后的包通过xftp上传到服务器

-
解压,我这边是解压到/usr/local目录下
-- 创建路径 mkdir /usr/local/redis -- 解压 tar -zxvf redis-4.0.0.tar.gz -C /usr/local/redis -
为防止编译失败,需要先安装gcc
yum -y install gcc -
编译
```-- 进入安装目录cd /usr/local/redis/redis-4.0.0-- 编译make``` -
安装
make install
-
启动,有三种启动方式
-- 直接启动 redis-server-- 指定配置文件启动 redis-server redis.conf
-
关闭redis
方式一
-- 查看redis进程 ps aux | grep redis-- 杀掉进程 kill -9 进程号
方式二
redis-cli shutdown
-
redis连接
-- 直接连接,默认连接本机的6379端口redis服务 redis-cli-- 指定ip连接 redis-cli -h 192.168.40.122 -P 6379
-
客户端退出
以下两种都可以 exitquit
二、redis配置文件
-
备份和打开
-- 进入目录 /usr/local/redis/redis-4.0.0-- 文件备份 cp /usr/local/redis/redis-4.0.0/redis.conf redis_bak.conf-- 打开配置文件 vim redis.conf -
内容详解
(1)daemonize
守护进程,默认是no,改为yes启动的时候就不会占用窗口 ,即默认后台启动

(2)bind 127.0.0.1
将图中这个注释掉,这个是限制了本机访问,注释掉才可以远程访问
(3) 设置密码
因为允许远程访问,所以一般要设置密码,添加
-
重启服务
如果修改了配置文件,就需要指定配置文件重启redis-server /usr/local/redis/redis-4.0.0/redis.conf
-
redis重新连接
--这里需要密码登录,否则无法使用 redis-cli -h 192.168.40.122 -a 123456
相关文章:

Redis安装及其配置文件修改
一、redis 安装 点击即可下载 https://download.redis.io/releases/ 将下载后的包通过xftp上传到服务器 解压,我这边是解压到/usr/local目录下 -- 创建路径 mkdir /usr/local/redis -- 解压 tar -zxvf redis-4.0.0.tar.gz -C /usr/local/redis 为防止编译失败&am…...
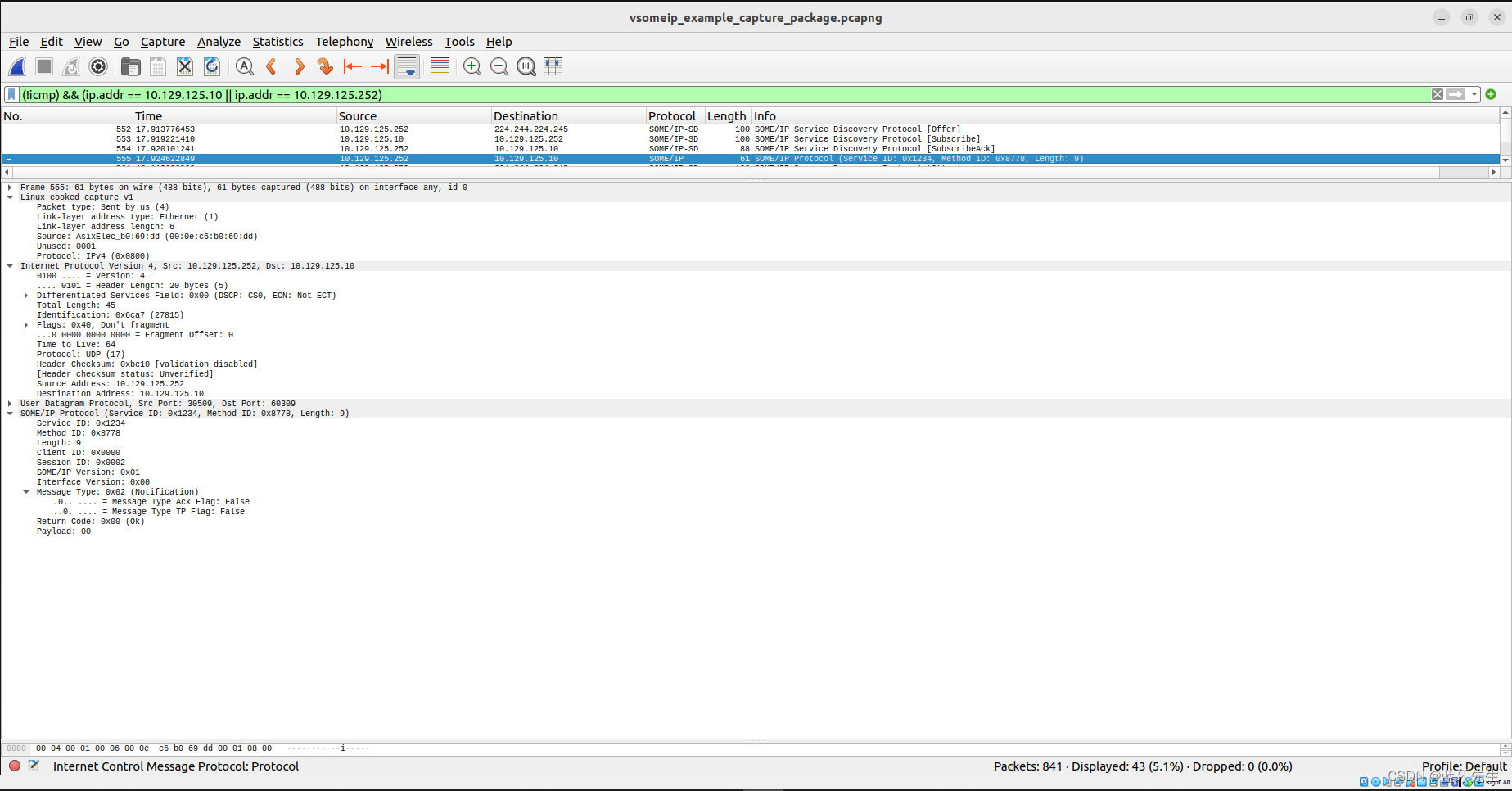
VSOMEIP3抓包数据
环境 $ cat /etc/os-release NAME"Ubuntu" VERSION"20.04.6 LTS (Focal Fossa)" IDubuntu ID_LIKEdebian PRETTY_NAME"Ubuntu 20.04.6 LTS" VERSION_ID"20.04" HOME_URL"https://www.ubuntu.com/" SUPPORT_URL"https:/…...

基于PyQt5的图形化界面开发——Windows内存资源监视助手[附带编译exe教程]
基于PyQt5的图形化界面开发——Windows内存资源监视助手[附带编译exe教程] 0. 前言1. 资源信息获取函数——monitor.py2. UI界面——listen.py3. main.py4. 运行效果5. 编译 exe 程序6. 其他PyQt文章 0. 前言 利用 PyQt5 开发一个 windows 的资源监视助手,在使用虚…...

Linus Torvalds发布了第一个Linux内核6.4候选版本
导读自Linux内核6.3发布和下一个内核系列Linux 6.4的合并窗口开放以来,已经过去了一段时间,近日,Linus Torvalds发布了第一个RC(候选发布版)的里程碑,供公众测试。 为期两周的Linux内核6.4合并窗口现已关闭…...
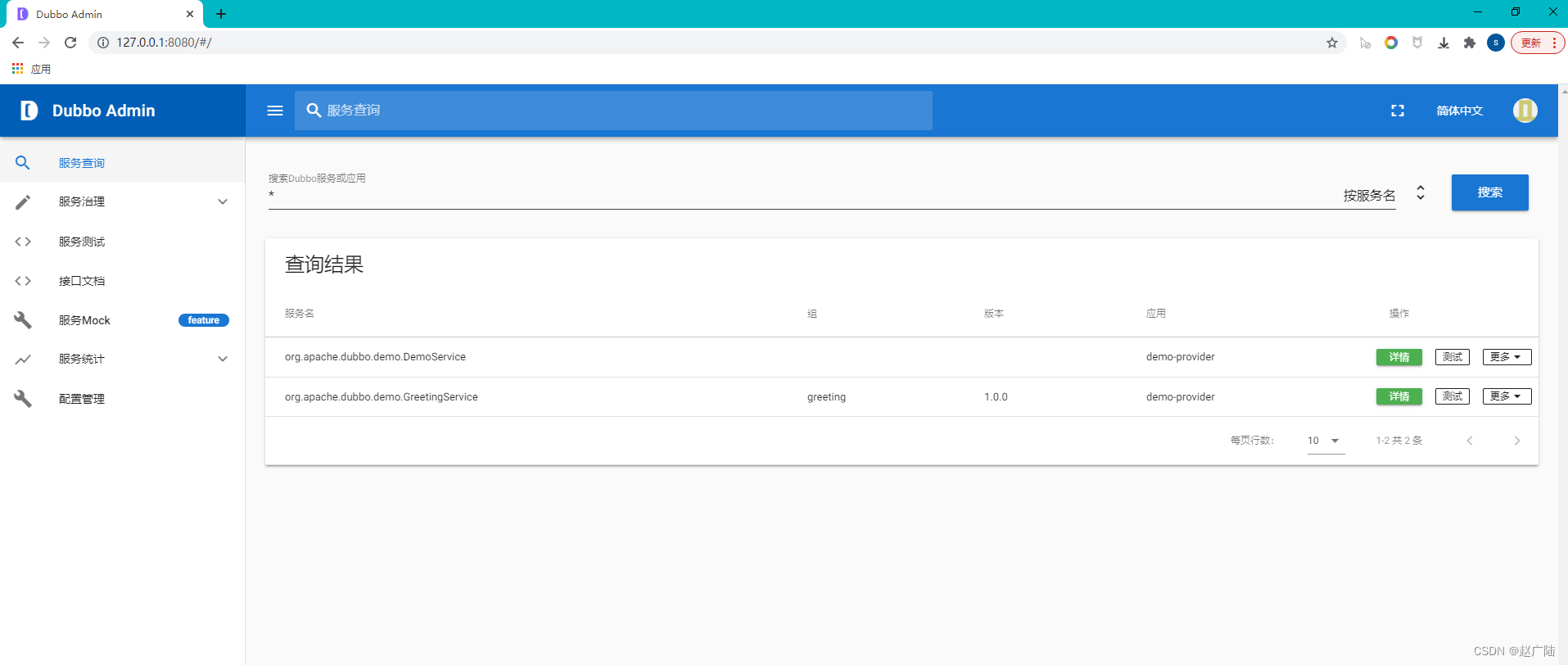
由浅入深Dubbo核心源码剖析环境介绍
目录 1 框架介绍1.1 概述1.2 运行架构1.3 整体设计 2 环境搭建2.1 源码拉取2.2 源码结构2.3 环境导入2.4 测试2.5 管理控制台 1 框架介绍 1.1 概述 Dubbo是阿里巴巴公司开源的一个高性能优秀的服务框架,使得应用可通过高性能的 RPC 实现服务的输出和输入功能&#…...

Java 远程连接 SQLite 数据库
Java 可以使用 JDBC API 来连接 SQLite 数据库。但是,SQLite 不支持远程连接,因为它是一种文件数据库,需要直接访问数据库文件。 如果您需要从远程位置访问 SQLite 数据库,可以将 SQLite 数据库文件放在共享文件夹中,…...
)
网安面试题大全(附答案)
本文面试题汇总: 防范常见的 Web 攻击 重要协议分布层 arp协议的工作原理 rip协议是什么?rip的工作原理 什么是RARP?工作原理 OSPF协议?OSPF的工作原理 TCP与UDP区别总结 什么是三次握手四次挥手? tcp为什么要三次握手…...
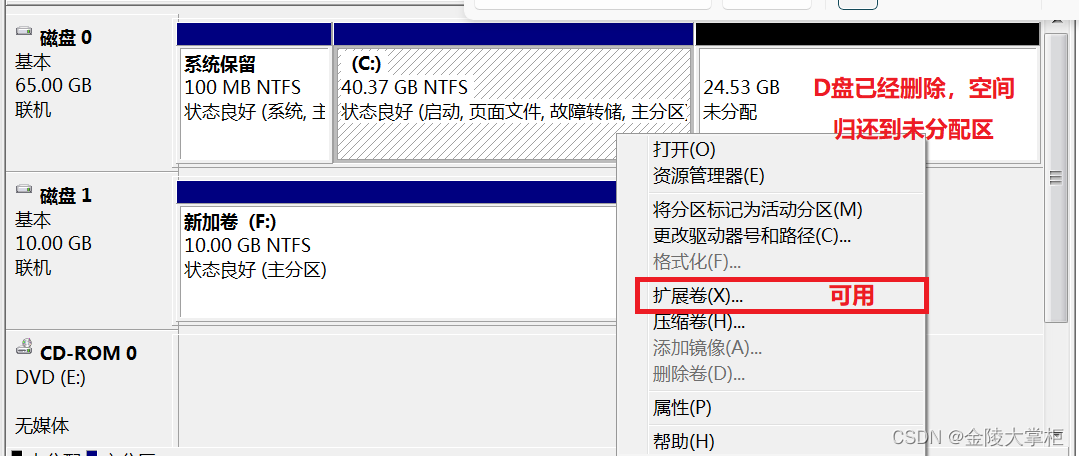
windows 系统扩容C盘注意事项
windows系统大家都不陌生,是大家用的最多的操作系统。在实际的使用中,遇到需要扩容C盘的情况不是很多,但是如果遇到了,有以下几个事项需要大家注意: 剩余空间是否充足 不论当前服务器是物理服务器还是虚拟机ÿ…...
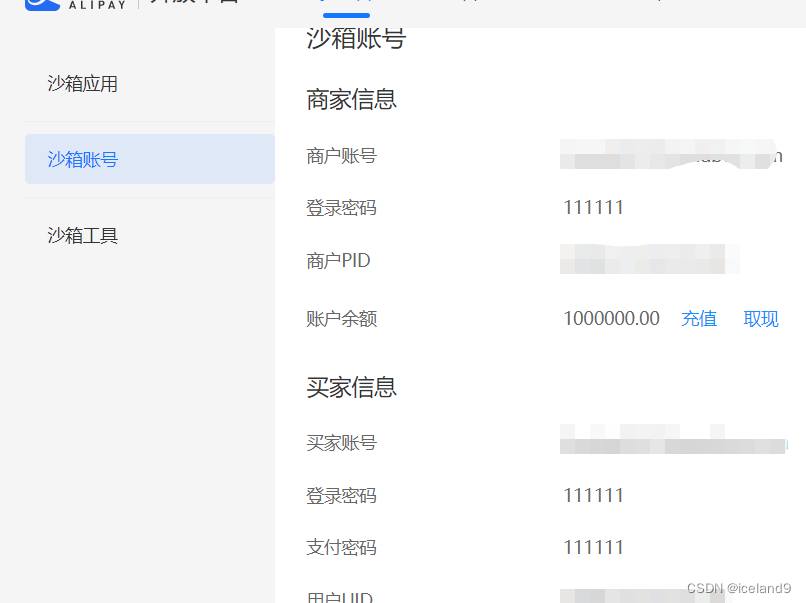
接入支付宝沙箱环境
1、这里有几个重要数据要拿到,一个是支付宝的公钥和私钥,一个是支付的网关,和支付的APPID。这几个数据是要写到代码中的 官方手册:文档地址 1.1 配置沙箱应用环境 https://openhome.alipay.com/develop/sandbox/app 1.2 配置接口…...

用原生JS实现虚拟列表(IT枫斗者)
用原生JS实现虚拟列表 介绍 最近在开发需求的时候,有用到 Antd 的虚拟列表组件 rc-virtual-list ,粗略地看了一下源码,于是萌生了自己写一个虚拟列表的想法。当一个列表需要渲染大量数据的时候是非常耗时的,而且在列表滚动的过程…...
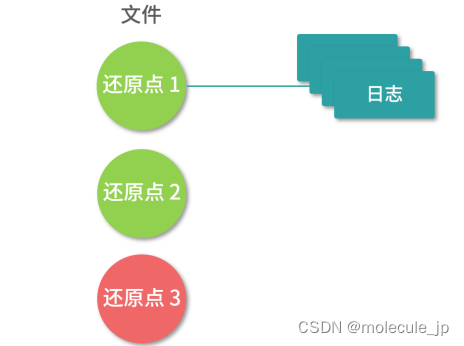
FAT NTFS Ext3文件系统有什么区别
10 年前 FAT 文件系统还是常见的格式,而现在 Windows 上主要是 NTFS,Linux 上主要是Ext3、Ext4 文件系统。关于这块知识,一般资料只会从支持的磁盘大小、数据保护、文件名等各种维度帮你比较,但是最本质的内容却被一笔带过。它们最…...

信息收集思路
1、开发者注释 在网站前端代码中遗留的开发者注释 其中可能包含某些关键信息 💡 使用F12 、CtrlU 、view-source: 查看前端源码 3、Robots文件 爬虫协议,网站根目录存在的robots.txt文件,用于告知搜索引擎或爬虫哪些路径和页面不…...

Tauri应用开发(二):创建第一个Tauri应用
创建tauri应用 推荐参考官方文档:https://tauri.app/v1/guides/ 创建命令: npm create tauri-applatest💡注意:请确保Node.js和Rust已经正确安装 在创建过程中,需要根据提示选择配置项。 主要配置有: 项目…...

自信裸辞:一晃 ,失业都3个月了.....
最近,找了很多软测行业的朋友聊天、吃饭 ,了解了一些很意外的现状 。 我一直觉得他们技术非常不错,也走的测开/管理的路径;二三月份裸辞的,然后一直在找工作,现在还没找到工作 。 经过我的分析࿰…...

Python3 输入和输出
在Python 3中,你可以使用内置的函数来进行输入和输出操作。 输入(Input): 要从用户那里获取输入,可以使用input()函数。input()函数会等待用户输入,并返回一个字符串。你可以将输入存储在一个变量中&#…...
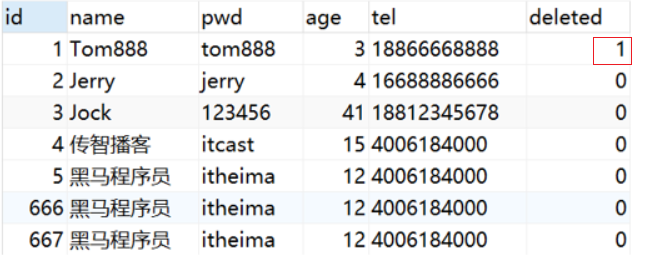
Mybatis Plus 使用@TableLogic实现逻辑删除
文章目录 步骤1:修改数据库表添加deleted列步骤2:实体类添加属性步骤3:运行删除方法知识点1:TableLogic 接下来要讲解是删除中比较重要的一个操作,逻辑删除,先来分析下问题: 这是一个员工和其所签的合同表,关系是一个员工可以签多…...

2023/5/23总结
super关键字 super关键字的用法和this 关键字的用法相似 this:代表本类对象的引用(this关键字指向调用该方法的对象一般我们是在当前类中使用this关键字,所以我们常说this代表本类对象的引用)super:代表父类存储空间的标识(可以理解为父类对象…...
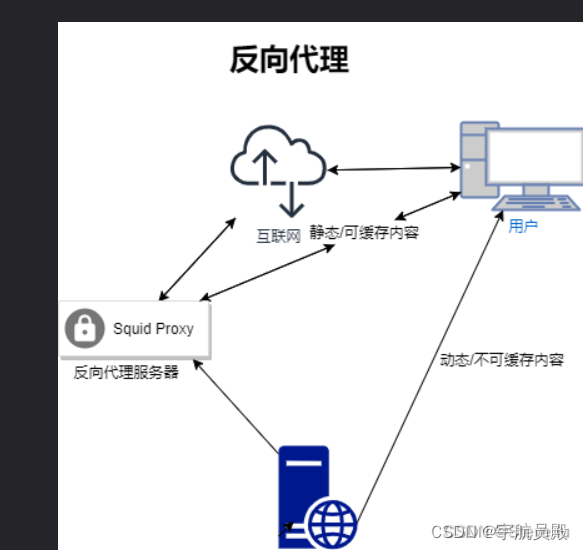
Squid代理服务器应用
在web架构中,用户一般进入负载均衡层,通过调度来访问web应用层,但是如果访问量太大,并发量较高,web应用层会吃不消,我们把静态资源、经常要访问的资源放入缓存,用户直接访问缓存层,加…...

网络编程中的sockfd是什么?
2023年5月22日,周一早上: 今天早上学习网络编程时遇到了sockfd这个变量,于是学习了一下,顺便写篇博客来记录自己的学习成功。 sockfd是什么意思? "sock"是socket的缩写。"fd"则是file descripto…...
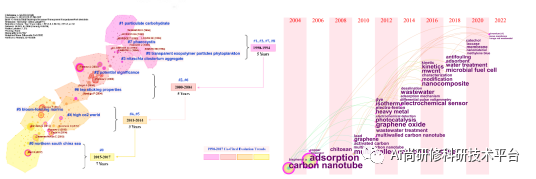
如何利用Citespace和vosviewer既快又好地写出高质量的论文及快速锁定热点和重点文献进行可视化分析?
基于Citespace和vosviewer文献计量学可视化SCI论文高效写作方法 CiteSpace是什么? 简单来说,它一款通过将国内外文献进行可视化分析来帮助你了解一门学科前世今生的软件。 面对成千上万篇的文献,怎样才能快速锁定自己最感兴趣的主题及科学…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...
