GAN和CycleGAN
文章目录
- 1. GAN 《Generative Adversarial Nets》
- 1.1 相关概念
- 1.2 公式理解
- 1.3 图片理解
- 1.4 熵、交叉熵、KL散度、JS散度
- 1.5 其他相关(正在补充!)
- 2. Cycle GAN 《Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks》
- 2.1 基础理论和推到
- 2.2 实验结果
- 2.3 限制和讨论
本BLOG是个人文章阅读和知识积累,有很多的相关基础知识介绍,小白可放心食用。但由于都是手打的,如果存在问题请联系修改,有的地方博主可能也会有疑问,标出的地方有懂的大佬可留言讨论。当前整理了GAN和CycleGAN的相关内容,接下来还会整理WGAN等内容。
1. GAN 《Generative Adversarial Nets》
Ian J. Goodfellow, Jean Pouget-Abadie, Yoshua Benjio etc.
https://dl.acm.org/doi/10.5555/2969033.2969125
1.1 相关概念
生成模型:学习得到联合概率分布P(x,y)P(x,y)P(x,y),即特征x和标签y同时出现的概率,然后可以求条件概率分布和其他概率分布。学习到的是数据生成的机制。
判别模型: 学习得到条件概率分布P(y∣x)P(y|x)P(y∣x),即在特征x出现的情况下标记y出现的概率
学习一个分布和近似一个分布?
1.2 公式理解
GAN的损失函数:
minGmaxDV(D,G)=Ex∼Pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))](1.1)\underset{G}{min}\underset{D}{max}V(D,G) = E_{x \sim P_{data}(x)}[log D(x)]+E_{z\sim p_{z}(z)}[log(1-D(G(z)))] \tag{1.1}GminDmaxV(D,G)=Ex∼Pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))](1.1)
为了学习数据x的分布pgp_gpg,定义了一个含有噪声的变量分布pz(z)p_z(z)pz(z);V是评分方程(这个值是越大越好的),G是一个生成器,D是一个判别器;训练D最大化真实数据和生成数据的区别,训练G最小化真实数据和生成数据的区别;
注意这个公式有两项,第一项是指是否能正确识别真实的数据;第二项是指是否能够识别生成的数据;
(1) 完美D
- 当D(x)D(x)D(x)完美识别真实数据和生成数据,Ex∼Pdata(x)[logD(x)]E_{x\sim P_{data}(x)}[log D(x)]Ex∼Pdata(x)[logD(x)]趋近于1,而Ez∼pz(z)[log(1−D(G(z)))]E_{z\sim p_{z}(z)}[log(1-D(G(z)))]Ez∼pz(z)[log(1−D(G(z)))]趋近于0,整体趋近于1.
- 当DDD不完美的时候,由于存在logloglog会使得两项都是一个负数;那训练的目的就是使得这个负数尽量小
- 因此需要最大化判别器带来的值,来使得判别器D最佳。
(2) 完美G
- G只和Ez∼pz(z)[log(1−D(G(z)))]E_{z\sim p_{z}(z)}[log(1-D(G(z)))]Ez∼pz(z)[log(1−D(G(z)))]相关,如果G完美忽悠D的时候,Ez∼pz(z)[log(1−D(G(z)))]E_{z\sim p_{z}(z)}[log(1-D(G(z)))]Ez∼pz(z)[log(1−D(G(z)))]输出的结果就是负无穷;
- 当不是那么完美的时候,输出的值就是一个负数;我们目的是使得这个输出尽量小,以使得生成器最佳。
- 所以需要最小化生成器带来值Ez∼pz(z)[log(1−D(G(z)))]E_{z\sim p_{z}(z)}[log(1-D(G(z)))]Ez∼pz(z)[log(1−D(G(z)))]
训练过程
训练D说明
生成器生成的数据就是V(G,D)的第二项的输入:g(z)=xg(z) = xg(z)=x,那么对z的求和就可以变为对x的求和。
将V(G,D)V(G,D)V(G,D)展开成积分/求和的形式
V(G,D)=∫xpdata⋅log(D(x))dx+∫zpz(z)⋅log(1−D(g(z)))=∫xpdata⋅log(D(x))+pg(x)⋅log(1−D(x))dx(1.2)\begin{aligned} V(G,D) &= \int_x p_{data} \cdot log(D(x))dx + \int_z p_z(z) \cdot log(1-D(g(z))) \\ &=\int_x p_{data} \cdot log(D(x)) + p_g(x) \cdot log(1-D(x))dx \end{aligned} \tag{1.2} V(G,D)=∫xpdata⋅log(D(x))dx+∫zpz(z)⋅log(1−D(g(z)))=∫xpdata⋅log(D(x))+pg(x)⋅log(1−D(x))dx(1.2)
对于 任意的(a,b)∈R2\{0,0}(a,b) \in R^2 \backslash \{0,0\}(a,b)∈R2\{0,0},函数y→alog(y)+blog(1−y)y \rightarrow a log(y) + blog(1-y)y→alog(y)+blog(1−y)是一个凸函数,我们需要求这个函数的最大值,就求导数
ay+b1−y=0y=aa+b\begin{aligned} \frac{a}{y}+\frac{b}{1-y} = 0 \\ y = \frac{a}{a+b} \end{aligned} ya+1−yb=0y=a+ba
则在y=aa+by = \frac{a}{a+b}y=a+ba的时候有最大值,对应于判别器的概率即为:
DG∗(x)=pdata(x)pdata(x)+pg(x)D_G^*(x) = \frac{p_{data}(x)}{p_{data}(x) + p_g(x)}DG∗(x)=pdata(x)+pg(x)pdata(x)
将最优解带入到价值函数之中
C(G)=maxDV(G,D)=Ex∼pdata[logDG∗(x)]+Ez∼pz[log(1−DG∗(G(z)))]=Ex∼pdata[logpdata(x)pdata(x)+pg(x)]+Ex∼pg[logpg(x)pdata(x)+pg(x)](1.3)\begin{aligned} C(G) &= \underset{D}{max}V(G,D) \\ &= E_{x \sim p_{data}}[log D_G^*(x)] + E_{z \sim p_z}[log(1-D_G^*(G(z)))] \\ &= E_{x \sim p_{data}}[log \frac{p_{data}(x)}{p_{data}(x) + p_g(x)}] + E_{x \sim p_g}[log \frac{p_g(x)}{p_{data}(x) + p_g(x)}] \end{aligned} \tag{1.3} C(G)=DmaxV(G,D)=Ex∼pdata[logDG∗(x)]+Ez∼pz[log(1−DG∗(G(z)))]=Ex∼pdata[logpdata(x)+pg(x)pdata(x)]+Ex∼pg[logpdata(x)+pg(x)pg(x)](1.3)
根据KL散度和JS散度的定义,可以将上面的公式改写为
C(G)=KL(Pdata∣∣pdata+pg2)+KL(pg∣∣pdata+pg2)−log(4)=2⋅JSD(pdata∣∣pg)−log(4)(1.4)\begin{aligned} C(G) &= KL(P_{data} || \frac{p_{data}+p_g}{2}) + KL(p_g || \frac{p_{data}+p_g}{2}) -log(4) \\ &= 2 \cdot JSD(p_{data}||p_g) - log(4) \end{aligned} \tag{1.4} C(G)=KL(Pdata∣∣2pdata+pg)+KL(pg∣∣2pdata+pg)−log(4)=2⋅JSD(pdata∣∣pg)−log(4)(1.4)
注意pdata+pg2\frac{p_{data}+p_g}{2}2pdata+pg这里除以2是为了保证是一个分布(即概率的积分是等于1的)
在固定D训练G的时候,我们就是为了最小化这个C(G)C(G)C(G),根据上面推导:
所以给出结论:当pg=pdp_g = p_dpg=pd时,DG∗(x)=12D_G^*(x) = \frac{1}{2}DG∗(x)=21,因此C(G)=log12+12=−log4C(G) = log\frac{1}{2} + \frac{1}{2} = -log4C(G)=log21+21=−log4,可以得到最小的C(G)C(G)C(G)
1.3 图片理解
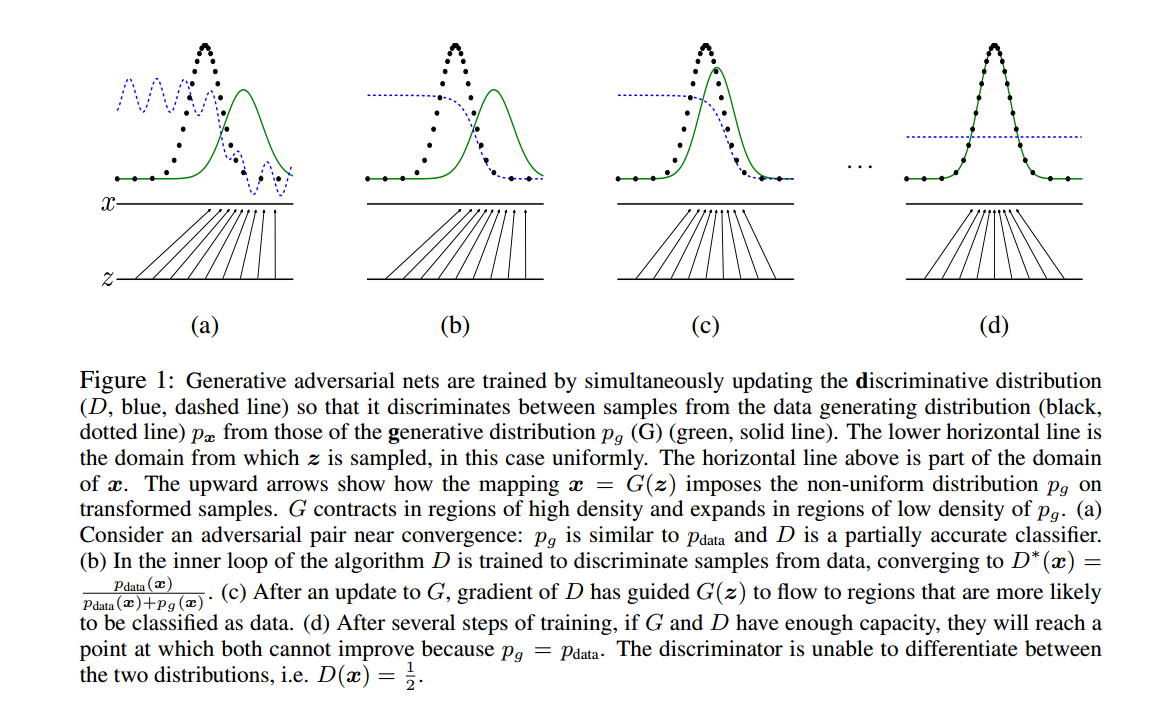
绿色是生成的分布;黑色是真实分布;蓝色是判别器的分布
(b)表示训练辨别器,使得辨别器可以非常好地区分二者
©表示训练生成器,继续欺骗判别器
1.4 熵、交叉熵、KL散度、JS散度
熵(Entropy)
K-L散度源于信息论,常用的信息度量单位为熵(Entropy)
H=−∑i=1Np(xi)⋅logp(xi)H = -\sum_{i=1}^{N}p(x_i) \cdot logp(x_i)H=−i=1∑Np(xi)⋅logp(xi)
注意这个对数没有确定的底数(可以使2、e或者10)。
熵度量了数据的信息量,可以帮助我们了解用概率分布近似代替原始分布的时候我们到底损失了多少信息;但问题是如何将熵值压缩到最小值,即如何编码可以达到最小的熵(存储空间最优化)。
-
交叉熵: 量化两个概率分布之间的差异
H(p,q)=−∑xp(x)logq(x)H(p,q) = -\sum_{x}p(x) \; log \; q(x)H(p,q)=−x∑p(x)logq(x) -
KL散度(kullback-Leibler divergence):量化两种概率分布 P和Q之间差异的方式,又成为相对熵
将熵的定义公式稍加修改就可以得到K-L散度的定义公式:
DKL(P∣∣Q)=∑i=1Np(xi)⋅(logp(xi)−logq(xi))=∑i=1Np(xi)⋅logp(xi)q(xi)D_{KL}(P||Q) = \sum_{i=1}^{N} p(x_i) \cdot (log p(x_i) - log q(x_i)) = \sum_{i=1}^{N}p(x_i) \cdot log \frac{p(x_i)}{q(x_i)}DKL(P∣∣Q)=i=1∑Np(xi)⋅(logp(xi)−logq(xi))=i=1∑Np(xi)⋅logq(xi)p(xi)
其中ppp和qqq分别表示数据的原始分布和近似的概率分布。
根据公式所示,K-L散度其实是数据的原始分布p和近似分布之间的对数差的期望。如果用2位底数计算,K-L散度表示信息损失的二进制位数,下面用期望表示式展示:
DKL(P∣∣Q)=E[logp(x)−q(x)]D_{KL}(P||Q) = E[log p(x) - q(x)]DKL(P∣∣Q)=E[logp(x)−q(x)]
注意:
- 从散度的定义公式中可以看出其不符合对称性(距离度量应该满足对称性)
- KL散度非负性
JS散度(Jensen-shannon divergence)
由于K-L散度是非对称的,所以对其进行修改,使得其能够对称,称之为 JS散度
(1) 设 M=12(P+Q)M = \frac{1}{2}(P+Q)M=21(P+Q),则:
DJS(P∣∣Q)=12DKL(P∣∣M)+12DKL(Q∣∣M)D_{JS}(P||Q) = \frac{1}{2}D_{KL}(P||M) + \frac{1}{2}D_{KL}(Q||M)DJS(P∣∣Q)=21DKL(P∣∣M)+21DKL(Q∣∣M)
(2) 将KL散度公式带入上面
DJS=12∑i=1Np(xi)log(p(xi)p(xi)+q(xi)2)+12∑i=1Nq(xi)⋅log(q(xi)p(xi)+q(xi)2)D_{JS} = \frac{1}{2}\sum_{i=1}^{N}p(x_i)log(\frac{p(x_i)}{\frac{p(x_i) + q(x_i)}{2}}) + \frac{1}{2}\sum_{i=1}^{N}q(x_i) \cdot log(\frac{q(x_i)}{\frac{p(x_i)+q(x_i)}{2}})DJS=21i=1∑Np(xi)log(2p(xi)+q(xi)p(xi))+21i=1∑Nq(xi)⋅log(2p(xi)+q(xi)q(xi))
(3) 将logloglog中的12\frac{1}{2}21放到分子上
DJS=12∑i=1Np(xi)log(2p(xi)p(xi)+q(xi))+12∑i=1Nq(xi)⋅log(2q(xi)p(xi)+q(xi))D_{JS} = \frac{1}{2}\sum_{i=1}^{N}p(x_i)log(\frac{2p(x_i)}{p(x_i) + q(x_i)}) + \frac{1}{2}\sum_{i=1}^{N}q(x_i) \cdot log(\frac{2q(x_i)}{p(x_i)+q(x_i)})DJS=21i=1∑Np(xi)log(p(xi)+q(xi)2p(xi))+21i=1∑Nq(xi)⋅log(p(xi)+q(xi)2q(xi))
(4) 提出2
DJS=12∑i=1Np(xi)log(p(xi)p(xi)+q(xi))+12∑i=1Nq(xi)⋅log(q(xi)p(xi)+q(xi))+log(2)D_{JS} = \frac{1}{2}\sum_{i=1}^{N}p(x_i)log(\frac{p(x_i)}{p(x_i) + q(x_i)}) + \frac{1}{2}\sum_{i=1}^{N}q(x_i) \cdot log(\frac{q(x_i)}{p(x_i)+q(x_i)}) + log(2)DJS=21i=1∑Np(xi)log(p(xi)+q(xi)p(xi))+21i=1∑Nq(xi)⋅log(p(xi)+q(xi)q(xi))+log(2)
注意这里是因为∑p(x)=∑q(x)=1\sum p(x) = \sum q(x) = 1∑p(x)=∑q(x)=1
JS散度的缺陷:当两个分布完全不重叠的时候,几遍两个分布的中心离得很近,其JS散度都是一个常数,所以其获取的梯度是0,是没有办法进行更新的。而两个分布没有重叠的原因:从理论和经验而言,真实的数据分布其实是一个低维流形(不具备高维特征),而是存在一个嵌入在高维度的低维空间内。由于维度存在差异,数据很可能不存在分布的重合。
1.5 其他相关(正在补充!)
2. Cycle GAN 《Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks》
一开始是应用到图像风格迁移上面的

2.1 基础理论和推到
- 概念描述
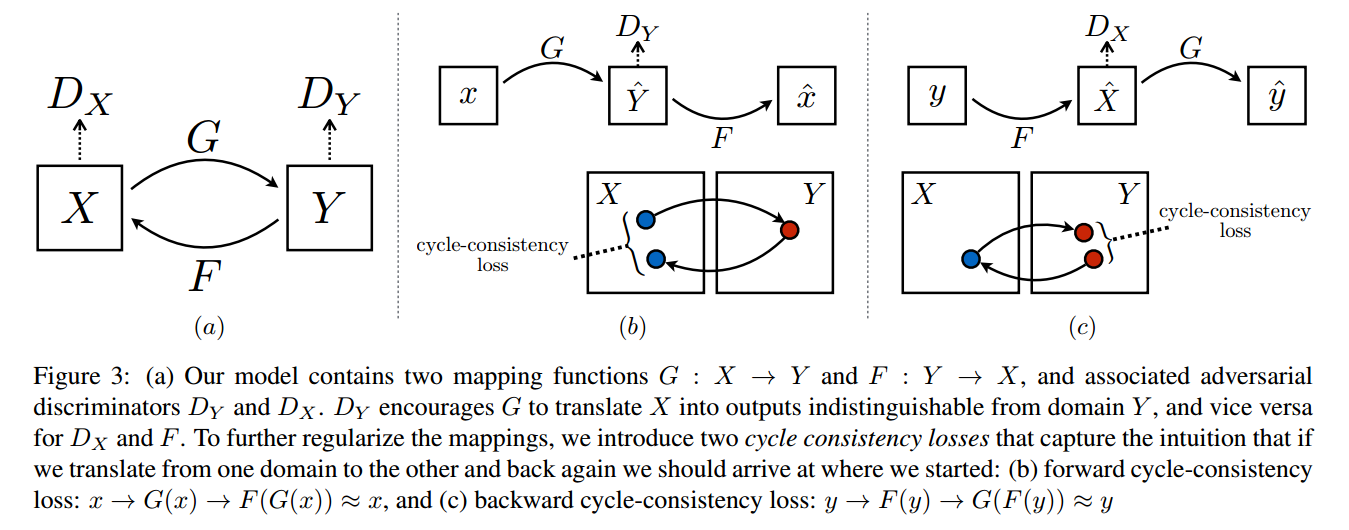
CycleGAN具有一个双判别器结构
- G:从X到Y的生成器
- F:从Y到X的生成器
- DxD_xDx:判别生成的X是真实X,还是生成的X
- DyD_yDy:判别生成的Y是真实Y,还是生成的Y
训练过程
- forward cycle-consistency loss
x→G(x)→F(G(x))≈xx \rightarrow G(x) \rightarrow F(G(x)) \approx xx→G(x)→F(G(x))≈x- 输入xxx,生成器GGG,得到输出y^=G(x)\hat{y} = G(x)y^=G(x),判别器DyD_yDy判别该输出是真实yyy还是生成的;
- 将y^\hat{y}y^继续输入到另一个生成器FFF之中,输出x^=F(y^)=F(G(x))\hat{x} = F(\hat{y}) = F(G(x))x^=F(y^)=F(G(x))
- backward cycle-consistency loss
y→F(y)→G(F(y))≈yy \rightarrow F(y) \rightarrow G(F(y)) \approx yy→F(y)→G(F(y))≈y- 输入yyy,生成器FFF,得到输出x^=F(y)\hat{x} = F(y)x^=F(y),判别器DxD_xDx判断该输出是真实xxx还是生成的;
- 将x^\hat{x}x^继续输入到另一个生成器GGG之中,输出y^=G(x^)=G(F(y))\hat{y} = G(\hat{x}) =G(F(y))y^=G(x^)=G(F(y))
损失函数
L(G,F,Dx,Dy)=LGAN(G,Dy,X,Y)+LGAN(F,Dx,Y,X)+λLcyc(G,F),(2.1)L(G,F,D_x,D_y) = L_{GAN}(G,D_y,X,Y) + L_{GAN}(F,D_x,Y,X) + \lambda L_{cyc}(G,F), \tag{2.1}L(G,F,Dx,Dy)=LGAN(G,Dy,X,Y)+LGAN(F,Dx,Y,X)+λLcyc(G,F),(2.1)
其中包含有两个原始GAN的损失和一个CycleGAN的损失。
G:X→YG:X \rightarrow YG:X→Y
LGAN(G,Dy,X,Y)=Ey∼pdata(y)[logDy(y)]+Ex∼pdata(x)[log(1−Dy(G(x)))],(2.2)L_{GAN}(G,D_y,X,Y) = E_{y \sim p_{data}(y)}[log D_y(y)] + E_{x \sim p_{data}(x)}[log(1 - D_y(G(x)))], \tag{2.2}LGAN(G,Dy,X,Y)=Ey∼pdata(y)[logDy(y)]+Ex∼pdata(x)[log(1−Dy(G(x)))],(2.2)
F:Y→XF:Y \rightarrow XF:Y→X
LGAN(F,Dy,X,Y)=Ex∼pdata(x)[logDx(x)]+Ey∼pdata(y)[log(1−Dx(F(y)))],(2.3)L_{GAN}(F,D_y,X,Y) = E_{x \sim p_{data}(x)}[log D_x(x)] + E_{y \sim p_{data}(y)}[log(1 - D_x(F(y)))], \tag{2.3}LGAN(F,Dy,X,Y)=Ex∼pdata(x)[logDx(x)]+Ey∼pdata(y)[log(1−Dx(F(y)))],(2.3)
在理论上,对抗学习可以学习到一种映射关系,以生成器G为例,它得到的输出的分布是与目标域是同分布。但是呢,在足够大的生成能力下,一个网络模型可以映射相同一系列输入图像到任意随机排列在目标域的图像中,其中任何一个学到的映射都可以得到与目标域匹配的输出分布。什么意思呢?就是可能有两个不同的生成器生成的图像都可能得到相同的能与目标域匹配的图像分布。为了得到一个满意的输出,因此单单一个对抗损失远远不够。为了进一步减少可能映射函数的空间域,作者认为学习到的映射因该具有循环一致性损失,就如我在方法中说的那样。
Lcyc(G,F)=Ex∼pdata(x)[∣∣F(G(x))−x∣∣1]+Ey∼pdata(y)[∣∣G(F(y))−y∣∣1].(2.4)L_{cyc}(G,F) = E_{x \sim p_{data}(x)}[||F(G(x)) -x||_1] + E_{y \sim p_{data}(y)}[||G(F(y)) - y||_1]. \tag{2.4}Lcyc(G,F)=Ex∼pdata(x)[∣∣F(G(x))−x∣∣1]+Ey∼pdata(y)[∣∣G(F(y))−y∣∣1].(2.4)
2.2 实验结果



2.3 限制和讨论
- 限制:
- 并非所有的例子都是非常好的效果的
- 颜色风格的变化容易实现,但是几何风格的变化难以实现
- 训练数据的特征分布会影响训练的过程,容易导致训练失败(比如只是用马和斑马进行训练,如果加入人骑在马上面进行风格迁移就会失败,因为没有学习到这个特征)
- 成对训练数据和非成对数据训练的效果仍然存在较大的区别
相关文章:

GAN和CycleGAN
文章目录1. GAN 《Generative Adversarial Nets》1.1 相关概念1.2 公式理解1.3 图片理解1.4 熵、交叉熵、KL散度、JS散度1.5 其他相关(正在补充!)2. Cycle GAN 《Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Ne…...
源码项目中常见设计模式及实现
原文https://mp.weixin.qq.com/s/K8yesHkTCerRhS0HfB0LeA 单例模式 单例模式是指一个类在一个进程中只有一个实例对象(但也不一定,比如Spring中的Bean的单例是指在一个容器中是单例的) 单例模式创建分为饿汉式和懒汉式,总共大概…...
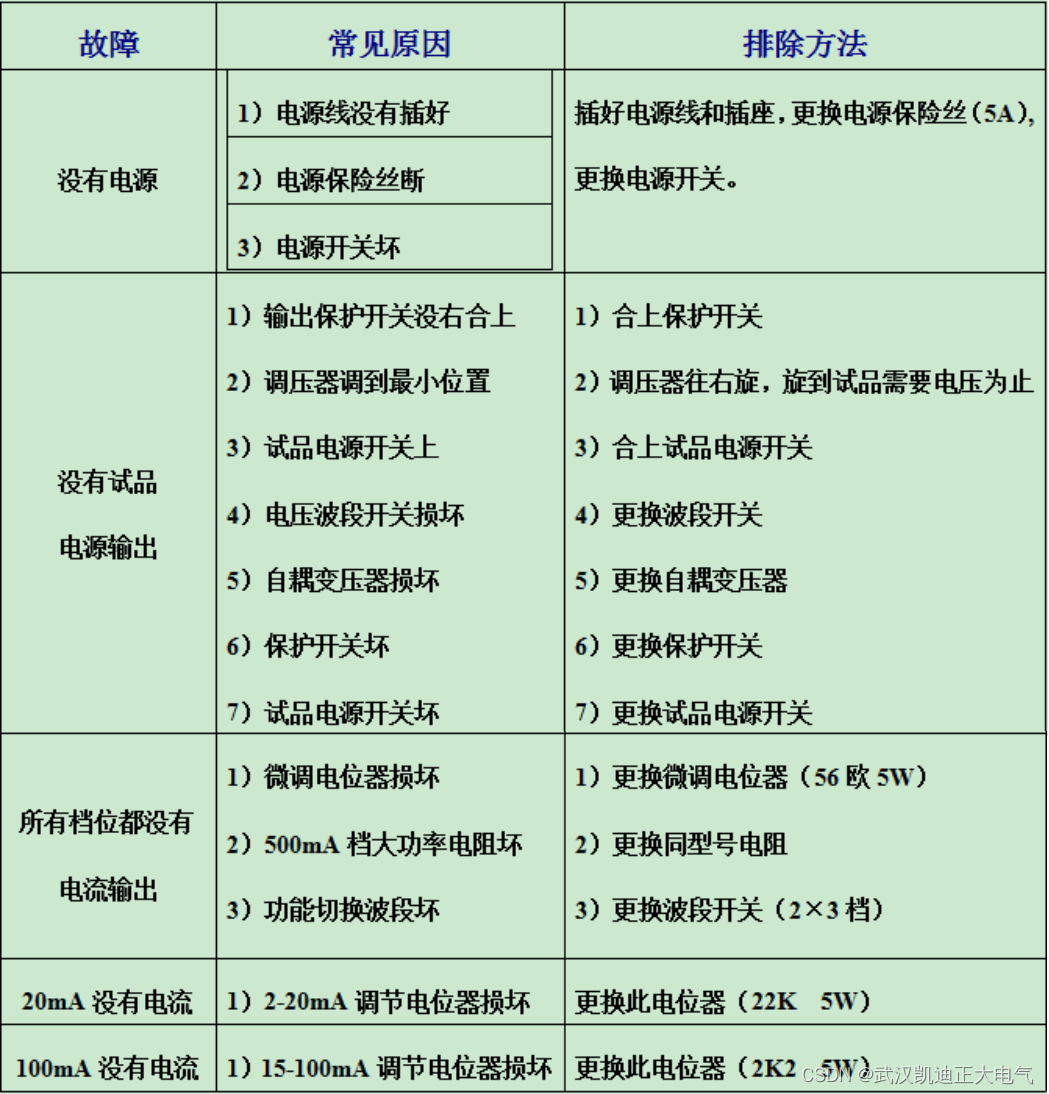
KDNM5000-10A-2剩余电流保护器测试仪
一、产品概述 KDNM5000-10A-2型剩余电流保护器测试仪(以下简称测试仪),是本公司改进产品,是符合国家标准《剩余电流动作保护器》(GB6829—95)中第8.3条和GB16917.1—1997中第9.9条验证AC型交流脱扣器动作特性要求的专用测试仪器。…...

C++实现线程池
C实现线程池一、前言二、线程池的接口设计2.1、类封装2.2、线程池的初始化2.3、线程池的启动2.4、线程池的停止2.5、线程的执行函数run()2.6、任务的运行函数2.7、等待所有线程结束三、测试线程池四、源码地址总结一、前言 C实现的线程池,可能涉及以下知识点&#…...
2023最新Java面试手册(性能优化+微服务架构+并发编程+开源框架)
Java面试手册 一、性能优化面试专栏 1.1、 tomcat性能优化整理 1.2、JVM性能优化整理 1.3、Mysql性能优化整理 二、微服务架构面试专栏 2.1、SpringCloud面试整理 2.2、SpringBoot面试整理 2.3、Dubbo面试整理 三、并发编程高级面试专栏 四、开源框架面试题专栏 4.1、Sprin…...

对灵敏度分析技术进行建模(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
完整爬虫学习笔记(第一章)
文章目录前言:fu:. 爬虫概述:hotdog:原理解剖:one: 服务器渲染:two: 前端JS渲染:fire: 第一个爬虫程序案例总结前言 最近正在学习Python网络爬虫的相关知识,鉴于本人Python水平有限 , 对Python并无太深的理解,所以此文章的主要目的在于抛砖引玉…...
会计师项目管理软件是什么,哪些必不可少的功能
欢迎阅读现代金融专业人士的会计师项目管理指南。在本文中,我们将深入探讨在基于项目的会计的各个方面使用项目管理方法的好处。我们还将教您面临哪些挑战以及如何为您的团队选择最佳工具。 为什么会计师的项目管理很重要? 在会计方面,目标始…...

第 8 章 优化
目录 8.1 优化概述 8.2 优化 SQL 语句 8.3 优化和指标 8.4 优化数据库结构 8.5 优化 InnoDB 表 8.6 优化 MyISAM 表 8.7 内存表的优化 8.8 了解查询执行计划 8.9 控制查询优化器 8.10 缓冲和缓存 8.11 优化锁定操作 8.12 优化 MySQL 服务器 8.13 衡量性能ÿ…...

剑指offer -- java题解
剑指offer -- java题解刷题地址1、数字在升序数组中出现的次数2、二叉搜索树的第k个节点3、二叉树的深度4、数组中只出现一次的两个数字5、和为S的两个数字6、左旋转字符串7、滑动窗口的最大值8、扑克牌顺子9、孩子们的游戏(圆圈中最后剩下的数)10、买卖股票的最好时机(一)刷题…...

若依ruoyi——手把手教你制作自己的管理系统【二、修改样式】
阿里图标一( ̄︶ ̄*)) 图片白嫖一((* ̄3 ̄)╭ ********* 专栏略长 爆肝万字 细节狂魔 请准备好一键三连 ********* 运行成功后: idea后台正常先挂着 我习惯用VScode操作 当然如果有两台机子 一个挂后台一个改前端就更好…...

2023.2.14每日一题——455. 分发饼干
每日一题题目描述解题核心解法一:双指针题目描述 题目链接:455. 分发饼干 假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。 对每个孩子 i,都有一个胃口值 g[i],…...

MySQL入门篇-MySQL常用字符函数小结
备注:测试数据库版本为MySQL 8.0 这个blog我们来聊聊常见的字符函数 函数名函数用途UPPER()返回大写的字符LOWER()返回小写的字符LTRIM()左边去掉空格TRIM()去掉空格RTRIM()右边去掉空格SPACE()返回指定长度的空格CONCAT()连接字符串CONCAT_WS()指定分隔符连接字符串CHAR_LEN…...
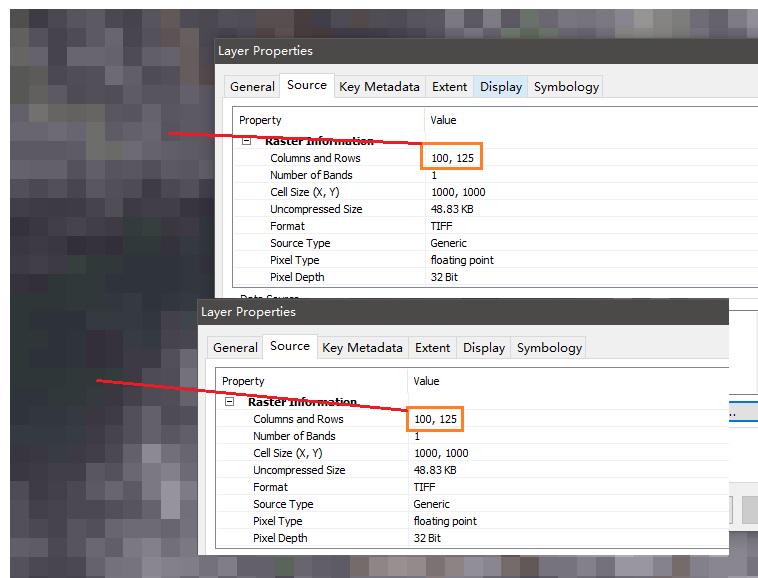
解决不同影像裁剪后栅格数据行列不一致问题
前言在处理栅格数据时,尽管用同一个矢量文件裁剪栅格数据,不同数据来源的栅格行列数也会出现不一致的情况。如果忽略或解决不好,会导致后续数据处理出现意想不到的误差或错误,尤其是利用编程实现数据处理时。因此,应当…...
visual studio2022配置opencv
标题:在vs下配置使用opencv 流程: 1、下载安装opencv 2、添加环境变量 3、vs中配置属性 4、使用 5、可能遇到的报错和解决 1、 下载安装opencv 官网下载地址: https://opencv.org/releases/ 我这里是windows环境,所以选择点击w…...

什么是销售管理?销售管理的五大职能
销售管理听起来很简单,似乎只是负责销售并确保客户满意,但事实上,它远不止于此。 销售管理的实际职能包括监督销售团队的工作,制定计划和设定目标,通常还包括确保销售流程的效率以获得最佳业务结果。 什么是销售管理…...

[CVPR‘22] EG3D: Efficient Geometry-aware 3D Generative Adversarial Networks
paper: https://nvlabs.github.io/eg3d/media/eg3d.pdfproject: EG3D: Efficient Geometry-aware 3D GANscode: GitHub - NVlabs/eg3d总结: 本文提出一种hybrid explicit-implicit 3D representation: tri-plane hybrid 3D representation,该方法不仅有…...

Learning C++ No.9【STL No.1】
引言: 北京时间:2023/2/13/18:29,开学正式上课第一天,直接上午一节思想政治,下午一节思想政治,生怕我们……,但,我深知该课的无聊,所以充分利用时间,把我的小…...
Apifox推荐-django后台验证token配置
最近事情很多,但是我还是想写一片推荐apifox的文章。 优秀的UI,清晰地逻辑,丰富的功能。对于我们这种业余选手来说,他真的很便利。 更新新版后有了更多贴心的功能,让你感觉他是一个有温度的工具。 最重要的是…...
SAS应用入门学习笔记6
SQL (SAS): Features: 1)不需要在每个query中重复调用每个SQL; 2)每个statement都是独立去完成的; 3)我们是没有proc print和proc sort语句的;(order by) key synta…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
