【C++】二叉树的非递归遍历
非递归遍历二叉树
- 一、二叉树的前序遍历
- 二、二叉树的中序遍历
- 三、二叉树的后序遍历
- 3.1 方法一
- 3.2 方法二
一、二叉树的前序遍历
题目链接
我们可以把任何一棵树看成左路节点,左路节点和右子树。先访问左路节点,再访问左路节点的右子树。在右子树中也重复这种循环,就是非递归遍历二叉树的思想。
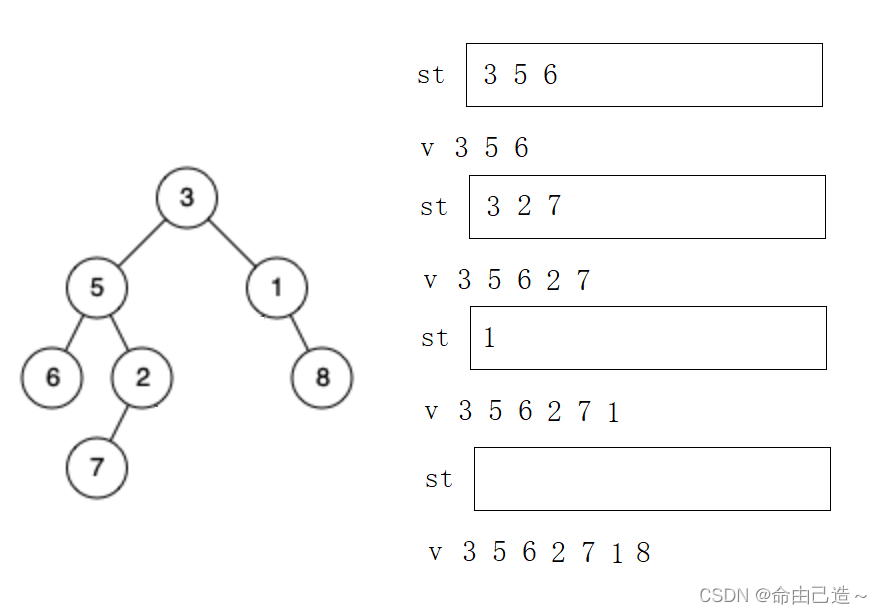
解释:
栈st存放节点,v存放数值,cur初始化为root。
循环条件是栈不为空或者cur不为空(访问最后一个节点之前栈就已经为空了),循环遍历左子树并且把左子树入栈,同时把值存入v中。然后弹出栈顶元素,并且把栈顶元素的右子树赋值给cur,这样就形成了遍历。
当栈不为空的时候说明还有左路节点的右子树没有被访问,当cur不为空的时候说明还有树要被访问。当同时为空的时候才是访问完成。当一个节点出栈的时候说明此时该节点及该节点的左子树已经被访问完成了。
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> v;TreeNode* cur = root;while(cur || !st.empty()){while(cur){st.push(cur);v.push_back(cur->val);cur = cur->left;}TreeNode* node = st.top();st.pop();cur = node->right;// 转化成子问题访问右子树}return v;}
};
二、二叉树的中序遍历
题目链接
因为中序遍历的访问顺序是左根右,跟前序遍历不同,所以我们让左节点入栈的时候先不访问,出栈(说明左子树访问完了)时在访问节点。
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> v;stack<TreeNode*> st;TreeNode* cur = root;while(!st.empty() || cur){while(cur){st.push(cur);cur = cur->left;}TreeNode* node = st.top();st.pop();v.push_back(node->val);cur = node->right;}return v;}
};
三、二叉树的后序遍历
3.1 方法一
首先我们知道后序遍历就是左右根,而我们可以把访问顺序变成根右左,然后再逆置顺序。而根右左就跟前序遍历的方法一样:
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> v;TreeNode* cur = root;while(cur || !st.empty()){while(cur){st.push(cur);v.push_back(cur->val);cur = cur->right;}TreeNode* node = st.top();st.pop();cur = node->left;}reverse(v.begin(), v.end());return v;}
};
3.2 方法二
按照常规的遍历方法走左右根,但是这里有一个问题:
当访问到根的时候有两种情况:
1️⃣ 从左子树回来,现在要先访问右子树
2️⃣ 从右子树回来,左右子树已经访问完毕,再访问根。
针对这种情况我们可以在加一个变量来确定是第几次访问根,如果是第一次就访问右子树,如果是第二次就访问。
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {stack<pair<TreeNode*, bool>> st;vector<int> v;TreeNode* cur = root;while(cur || !st.empty()){while(cur){st.push(make_pair(cur, false));cur = cur->left;}TreeNode* node = st.top().first;if(st.top().second == true){st.pop();v.push_back(node->val);}else{st.top().second = true;cur = node->right;}}return v;}
};
相关文章:

【C++】二叉树的非递归遍历
非递归遍历二叉树一、二叉树的前序遍历二、二叉树的中序遍历三、二叉树的后序遍历3.1 方法一3.2 方法二一、二叉树的前序遍历 题目链接 我们可以把任何一棵树看成左路节点,左路节点和右子树。先访问左路节点,再访问左路节点的右子树。在右子树中也重复这…...

Linux——线程同步(条件变量、POSIX信号量)和线程池
一.线程同步(一).概念线程同步是一种多线程关系,指的是线程之间按照特定顺序访问临界资源,进而能够避免线程饥饿问题。所谓线程饥饿指的是某个线程长期“霸占”临界资源,导致其他线程无法访问该资源。而通过线程同步机…...
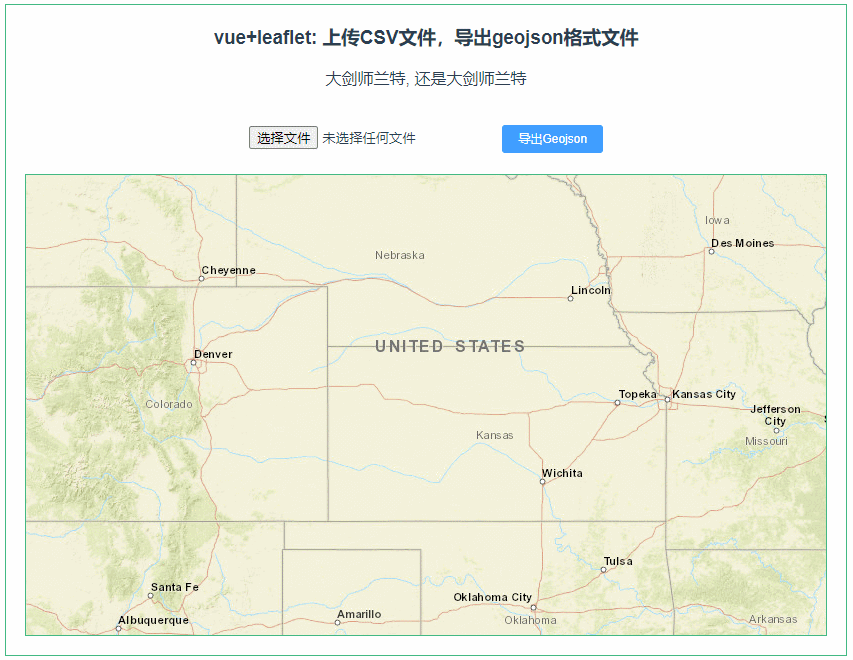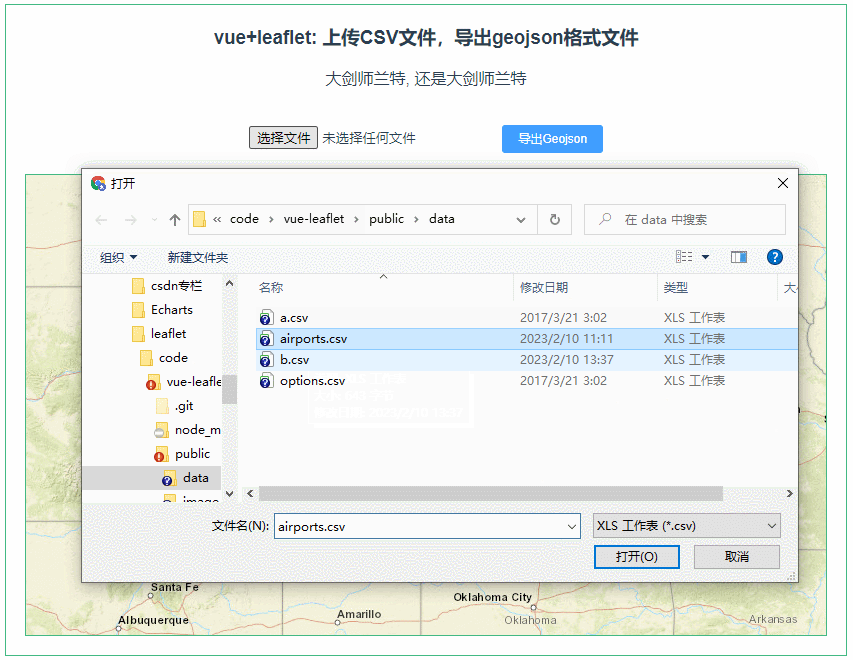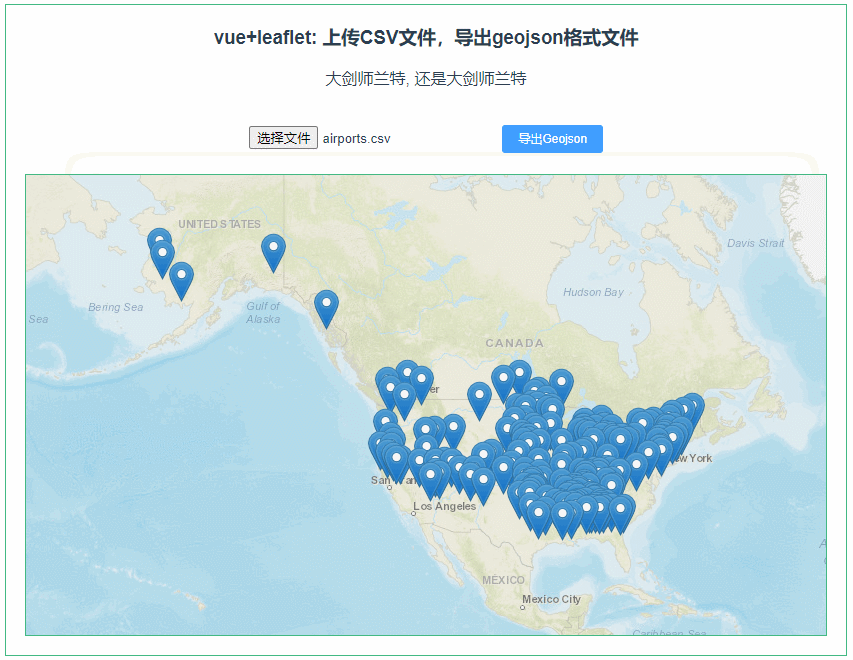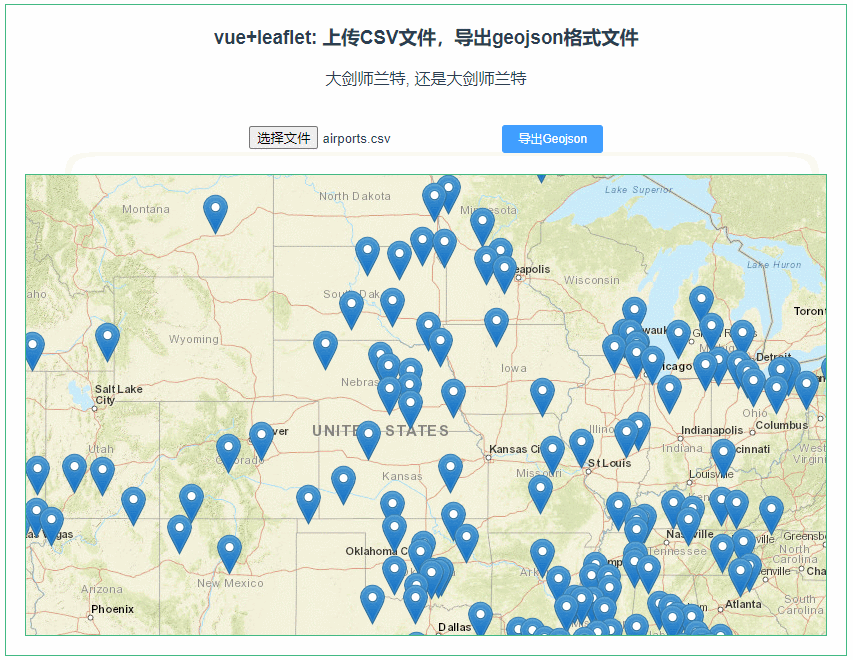
leaflet 上传CSV文件,导出geojson格式文件(064)
第064个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet中加载CSV文件,将图形显示在地图上。点击导出geojson,下载成geojson文件。 直接复制下面的 vue+openlayers源代码,操作2分钟即可运行实现效果. 文章目录 示例效果配置方式示例源代码(共114行)安装插件…...

Java内部类
文章目录一、内部类的概念二、内部类的分析三、内部类的分类1. 成员内部类2. 静态内部类3. 局部内部类4. 匿名内部类匿名内部类与Lambda表达式一、内部类的概念 在 Java 中,可以将一个类定义在另一个类里面或者一个方法里面,这样的类称为内部类。内部类…...
Centos系统里运行java的jar包
目前使用springboot开发是嵌入方式的tomcat,不需要单独使用tomcat,那么经常在服务器上运行jar包,这里记录一下在centos7系统里运行jar的方式。在运行之前需要确定centos7系统是否安装了java环境以及配置环境变量,还有jar需要运行的…...

招标采购流程的电子招标采购,是管理复杂供应链和多层供应商的高效方式。
负载均衡(Load Balance) 由于目前现有网络的各个核心部分随着业务量的提高,访问量和数据流量的快速增长,其处理能力和计算强度也相应地增大,使得单一的服务器设备根本无法承担。在此情况下,如果扔掉现有设…...

【C语言】C程序结构和基本语法
1、C语言程序结构 我们学习一门编程语言,第一个实例都是"hello world!",下面看一个最简单的C程序结构。 #include <stdio.h>int main() {/* 我的第一个 C 程序 */printf("Hello, World! \n");return 0; }程序的第一行 #incl…...

YOLOv8 目标检测 | 自定义数据集
本文介绍了使用用于目标检测的自定义数据训练 YOLOv8 模型。我正在使用来自 kaggle 的 yolo 格式的“Face Mask Dataset”,数据集链接如下:https://www.kaggle.com/datasets/maalialharbi/face-mask-dataset?resourcedownloadYOLOv8 是目前最先进的 YOL…...

Lua语法入门
注意:文章将持续更新完善 文章目录一. 初识Lua二. HelloWorld三. Lua的数据类型四. 变量五. 循环六. 函数七. 条件控制一. 初识Lua Lua 是一种轻量小巧的脚本语言,用标准C语言编写并以源代码形式开放, 其设计目的是为了嵌入应用程序中&#…...
)
华为OD机试真题JAVA实现【最小步骤数】真题+解题思路+代码(20222023)
🔥系列专栏 华为OD机试(JAVA)真题目录汇总华为OD机试(Python)真题目录汇总华为OD机试(C++)真题目录汇总华为OD机试(JavaScript)真题目录汇总文章目录 🔥系列专栏题目输入输出示例一输入输出说明示例二输入输出解题思路...

预检请求OPTIONS
这里写目录标题简单请求和非简单请求简单请求非简单请求预检请求OPTIONS简单请求和非简单请求 浏览器将请求分为两大类:简单请求(simple request)和非简单请求(not-so-simple request) 简单请求 简单请求࿰…...

引入短信服务发送手机验证码进行安全校验
其他方案>引入QQ邮箱发送验证码进行安全校验 相对短信验证码,操作更简单而且免费 最近想给自己的项目在注册时加点安全校验,准备使用免费的邮箱验证来着,在上一篇引入QQ邮箱进行安全校验时,看有朋友说阿里云会送一些短信服务免…...
opencv绘制直线
大家好,我是csdn的博主:lqj_本人 这是我的个人博客主页: lqj_本人的博客_CSDN博客-微信小程序,前端,python领域博主lqj_本人擅长微信小程序,前端,python,等方面的知识https://blog.csdn.net/lbcyllqj?spm1011.2415.3001.5343哔哩哔哩欢迎关注…...

Seata源码学习(五)- Seata服务端(TC)源码解读
Seata源码分析- Seata服务端(TC)源码解读 上节课我们已经分析到了SQL语句最终的执行器,但是再往下分析之前,我们需要先来分析一下TM客户端与TC端通讯以后,TC端的具体操作 服务端表解释 我们的Seata服务端在应用的时…...
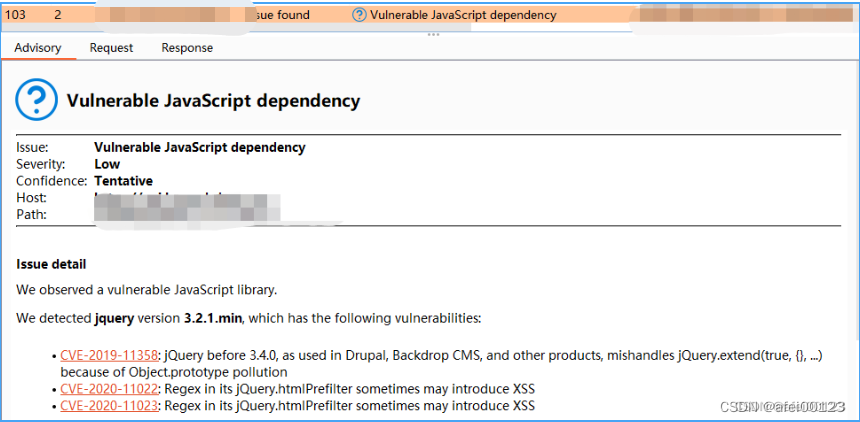
低版本jQuery导致XSS Nuclei FUZZ POC
目录 1.前言 2. Nuclei FUZZ jQuery XSS POC 3.漏洞验证 4.修复建议 1.前言 我记得以前用那些漏扫工具时时常会报一个低版本jQuery的安全问题,当时还不会验证。直到有一天,它托梦给我。我悟了。低版本jQuery导致XSS POC文件文末获取。...

【Linux】进程的描述组织与进程状态
文章目录🎪 进程的描述组织🚀1.什么是进程🚀2.进程的形成🚀3.进程标识符 *⭐3.1 PS命令查看PID⭐3.2 /proc目录查看进程属性🚀4.父子进程⭐4.1 系统调用获取PID⭐4.2 fork创建子进程⭐4.3 fork双返回值问题⭐4.4 写时拷…...

8.2.1.1 WHERE 子句优化
本节讨论可用于处理 WHERE 子句的优化。示例使用 SELECT 语句,但相同的优化适用于 DELETE 和 UPDATE 语句中的 WHERE 子句。 注意 因为 MySQL 优化器的工作正在进行,所以这里并没有记录 MySQL 执行的所有优化。 您可能会尝试重写查询以使算术运算更快&am…...

拆个微波炉,分析一下电路
微波炉是用2450MHz的超高频电磁波来加热食品,它能无损穿越塑料,陶瓷,不能穿越金属,碰到金属会反射,但穿过含水食物,食物内的分子会高速摩擦,产生热量,使食物变熟。在厨房电器中&…...

DM8:DMDSC共享存储集群搭建-共享存储绑定
DM8:DMDSC共享存储集群搭建-共享存储绑定环境介绍:1 发现共享磁盘2 对共享存储进行分区格式化2.1 格式化成功但不可用2.2 解决问题修改错误的分区格式3 配置/etc/rc.d/rc.local3.1 编辑文件(两个节点配置相同)3.2 使rc.local生效4 重启操作系…...

Spark OOM问题常见解决方式
文章目录Spark OOM问题常见解决方式1.map过程产生大量对象导致内存溢出2.数据不平衡导致内存溢出3.coalesce调用导致内存溢出4.shuffle后内存溢出5. standalone模式下资源分配不均匀导致内存溢出6.在RDD中,共用对象能够减少OOM的情况优化1.使用mapPartitions代替大部…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...
