AcWing《蓝桥杯集训·每日一题》—— 1460 我在哪?
AcWing《蓝桥杯集训·每日一题》—— 1460. 我在哪?
文章目录
- AcWing《蓝桥杯集训·每日一题》—— 1460. 我在哪?
- 一、题目
- 二、解题思路
- 三、代码实现
本次博客我是通过Notion软件写的,转md文件可能不太美观,大家可以去我的博客中查看:北天的 BLOG,持续更新中,另外这是我创建的编程学习小组频道,想一起学习的朋友可以一起!!!
一、题目
沿路有一排共 NNN 个农场。
不幸的是农场并没有编号,这使得约翰难以分辨他在这条路上所处的位置。
然而,每个农场都沿路设有一个彩色的邮箱,所以约翰希望能够通过查看最近的几个邮箱的颜色来唯一确定他所在的位置。
每个邮箱的颜色用 A..ZA..ZA..Z 之间的一个字母来指定,所以沿着道路的 NNN 个邮箱的序列可以用一个长为 NNN 的由字母 A..ZA..ZA..Z 组成的字符串来表示。
某些邮箱可能会有相同的颜色。
约翰想要知道最小的 A..ZA..ZA..Z 的值,使得他查看任意连续 KKK 个邮箱序列,他都可以唯一确定这一序列在道路上的位置。
例如,假设沿路的邮箱序列为 ABCDABC 。
约翰不能令 K=3K = 3K=3,因为如果他看到了 ABC,则沿路有两个这一连续颜色序列可能所在的位置。
最小可行的 K 的值为 K=4K = 4K=4,因为如果他查看任意连续 4 个邮箱,那么可得到的连续颜色序列可以唯一确定他在道路上的位置。
输入格式
输入的第一行包含 NNN,第二行包含一个由 NNN 个字符组成的字符串,每个字符均在 A..ZA..ZA..Z 之内。
输出格式
输出一行,包含一个整数,为可以解决农夫约翰的问题的最小 KKK 值。
数据范围
1≤N≤1001≤ N ≤1001≤N≤100
输入样例:
7
ABCDABC
输出样例:
4
二、解题思路
1、暴力枚举法
对于暴力枚举法,我们可以使用两重循环,外层循环枚举K的长度,内层循环枚举所有的子串,并在后面的部分中查找该子串是否出现过。如果没有找到,则表示当前长度K可行,输出K并结束程序。如果内层循环结束后仍未找到合适的K,则需要继续外层循环进行下一轮枚举。
2、二分法
对于二分法,我们可以将判断一个长度K是否可行转化为判断以每个位置为起点的长度为K的子串是否互不相同。具体地,我们可以将所有以长度K的子串存入一个集合中,然后判断集合中的元素个数是否等于N-K+1。如果等于,则表示当前长度K可行,否则不可行。因为如果有重复的子串,那么集合中的元素个数会小于N-K+1,如果没有重复的子串,则集合中的元素个数会等于N-K+1。根据这个判断结果来缩小二分法的搜索范围,直到找到最小可行的K。
三、代码实现
n = int(input()) # 输入农场数
s = input().strip() # 输入邮筒序列res = n # 初始化最小连续颜色长度res为nfor k in range(1, n+1): # 外层循环枚举连续颜色长度k,从1到nseen = set() # 定义一个集合seen,用于存储当前长度为k的所有子串unique = True # 初始化unique为True# 内层循环枚举字符串s中长度为k的所有子串for i in range(n-k+1):sub = s[i:i+k] # 取出从i开始长度为k的子串subif sub in seen: # 如果sub已经在seen中出现过了,说明有重复子串,此时unique为Falseunique = Falsebreakelse:seen.add(sub) # 否则将sub加入seen集合中if unique: # 如果unique为True,说明当前枚举的k值可以唯一确定任意连续k个邮箱序列在道路上的位置res = k # 更新最小连续颜色长度resbreakprint(res) # 输出最小的k值,即可以解决农夫约翰的问题的最小K值
该段代码的时间复杂度为 O(n2)O(n^2)O(n2),因为外层循环枚举了 kkk 个长度,内层循环每次需要枚举 n−k+1n-k+1n−k+1 个长度为 kkk 的子串,并且使用了 set 进行查重。set 的查找时间复杂度为 O(1)O(1)O(1),所以内层循环的时间复杂度为 O((n−k+1)×1)=O(n−k+1)O((n-k+1) \times 1) = O(n-k+1)O((n−k+1)×1)=O(n−k+1)。因此,总的时间复杂度为:∑k=1n(n−k+1)=O(n2)\sum_{k=1}^{n} (n-k+1) = O(n^2)∑k=1n(n−k+1)=O(n2)
其中,∑k=1n(n−k+1)\sum_{k=1}^{n} (n-k+1)∑k=1n(n−k+1) 是等差数列求和公式的展开形式。
二分解法:
n = int(input()) # 输入农场数
s = input().strip() # 输入邮筒序列def check(k): # 定义check函数用来检查k的取值是否满足条件substrings = set() # 用set存储s中所有长度为k的不同的子串for i in range(n-k+1):substrings.add(s[i:i+k])return len(substrings) == n-k+1 # 如果set中的元素个数为n-k+1则说明所有长度为k的子串均不相同left, right = 1, n # 初始时,left=1,right=n
while left < right: # 当left < right时,循环继续mid = (left+right)//2 # 计算中间值midif check(mid): # 如果check(mid)返回True,则说明k=mid满足条件,应该继续往左找right = midelse: # 如果check(mid)返回False,则说明k=mid不满足条件,应该往右找left = mid+1print(left) # 最终left就是满足条件的最小的k
该二分法代码的时间复杂度为O(nlogn)O(nlogn)O(nlogn)*,*其中nnn为字符串的长度。主要耗时的是check函数,时间复杂度为O(nk)O(nk)O(nk),kkk是检查的子串长度,当k=nk=nk=n时,时间复杂度最大为O(n2)O(n^2)O(n2)。而二分法中循环的次数最多为O(logn)O(logn)O(logn),因此总时间复杂度为O(n∗logn)O(n*logn)O(n∗logn)。
相关文章:

AcWing《蓝桥杯集训·每日一题》—— 1460 我在哪?
AcWing《蓝桥杯集训每日一题》—— 1460. 我在哪? 文章目录AcWing《蓝桥杯集训每日一题》—— 1460. 我在哪?一、题目二、解题思路三、代码实现本次博客我是通过Notion软件写的,转md文件可能不太美观,大家可以去我的博客中查看&am…...

AcWing《蓝桥杯集训·每日一题》—— 3729 改变数组元素
AcWing《蓝桥杯集训每日一题》—— 3729. 改变数组元素 文章目录AcWing《蓝桥杯集训每日一题》—— 3729. 改变数组元素一、题目二、解题思路三、代码实现本次博客我是通过Notion软件写的,转md文件可能不太美观,大家可以去我的博客中查看:北天…...

如何熟练掌握Python在气象水文中的数据处理及绘图【免费教程】
pythonPython由荷兰数学和计算机科学研究学会的吉多范罗苏姆于1990年代初设计,作为一门叫做ABC语言的替代品。Python提供了高效的高级数据结构,还能简单有效地面向对象编程。Python语法和动态类型,以及解释型语言的本质,使它成为多…...

Leetcode详解JAVA版
目录1. 两数之和14. 最长公共前缀15. 三数之和18. 四数之和19. 删除链表的倒数第 N 个结点21. 合并两个有序链表28. 找出字符串中第一个匹配项的下标36. 有效的数独42. 接雨水43. 字符串相乘45. 跳跃游戏 II53. 最大子数组和54. 螺旋矩阵55. 跳跃游戏62. 不同路径70. 爬楼梯73.…...
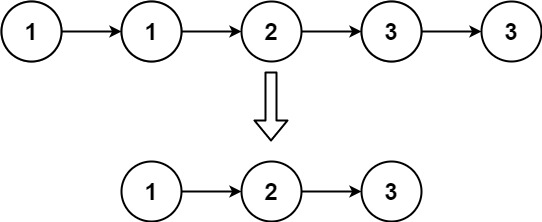
LeetCode 83. 删除排序链表中的重复元素
原题链接 难度:easy\color{Green}{easy}easy 题目描述 给定一个已排序的链表的头 headheadhead , 删除所有重复的元素,使每个元素只出现一次 。返回 已排序的链表 。 示例 1: 输入:head [1,1,2] 输出:…...

RMI简易实现(基于maven)
参考其它rmi(remote method invocation)的代码后,加入了自己思考。整个工程基于maven构建,我觉得maven的模块化可比较直观地演示rmi 目录 项目结构图 模块解读 pom文件 rmi-impl rmi-common-interface rmi-server rmi-cli…...

‘excludeSwitches‘ 的 [‘enable-logging‘] 和[‘enable-automation‘]
selenium 使用 chrome 浏览器的 chromedriver 时,可以加参数, chrome_optionswebdriver.ChromeOptions() chrome_options.add_experimental_option(excludeSwitches,[enable-logging]) chrome_options.add_experimental_option(excludeSwitches,[enable…...
| 真题+思路+考点+代码+岗位)
华为OD机试 - 最短木板长度(Python)| 真题+思路+考点+代码+岗位
最短木板长度 题目 小明有 n n n 块木板,第 i i i(1≤ i i...
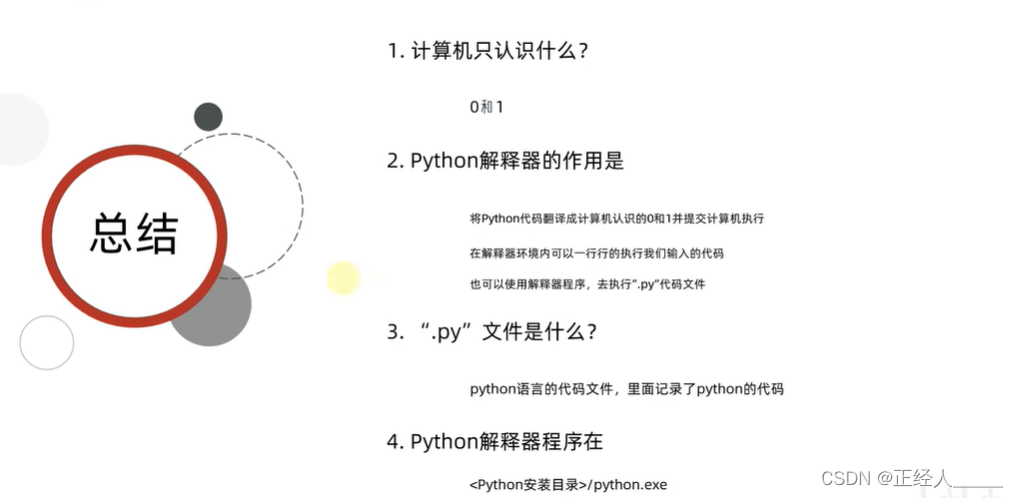
第一个Python程序-HelloWorld与Python解释器
数据来源 01 第一个Python程序-HelloWorld 1)打开cmd: windows R 打开运行窗口输入cmd 2)进入Python编写页面 输入:python 3)然后输入要写的Python代码然后回车 print("Hello World!!!") print() …...

C++数据类型
目录 一、基本的内置类型 二、typedef声明 三、枚举类型 一、基本的内置类型 C 为程序员提供了种类丰富的内置数据类型和用户自定义的数据类型。下表列出了七种基本的 C 数据类型: 类型关键字布尔型bool字符型char整型int浮点型float双浮点型double无类型void宽…...
| 真题+思路+考点+代码+岗位)
华为OD机试 - 考古学家(Python)| 真题+思路+考点+代码+岗位
考古学家 题目 有一个考古学家发现一个石碑 但是很可惜 发现时其已经断成多段 原地发现 N 个断口整齐的石碑碎片 为了破解石碑内容 考古学家希望有程序能帮忙计算复原后的石碑文字组合数 ,你能帮忙吗 备注: 如果存在石碑碎片内容完全相同,则由于碎片间的顺序不影响复原后…...
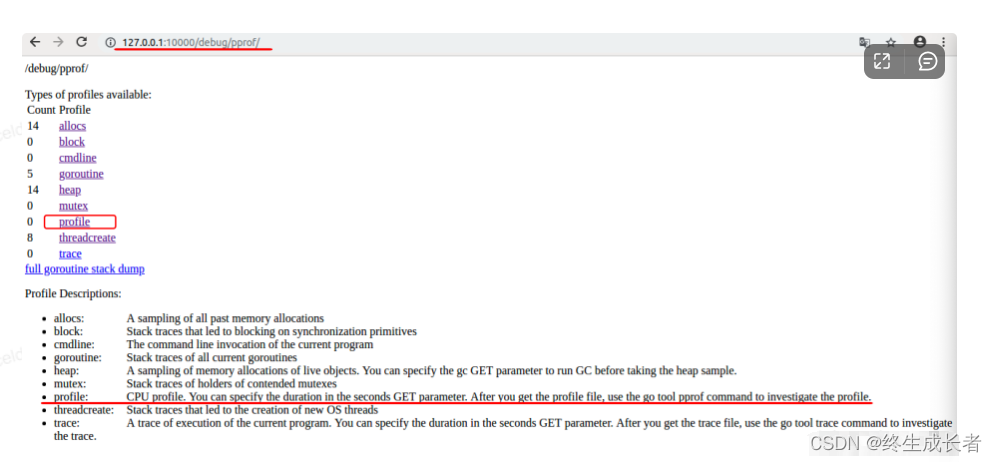
常用调试golang的bug以及性能问题的实践方法
文章目录如何分析程序运行时间和CPU利用率情况1.shell内置time指令/usr/bin/time指令如何分析golang程序的内存使用情况?1.内存占用情况查看如何分析golang程序的CPU性能情况1.性能分析注意事项2.CPU性能分析A.Web界面查看B.使用pprof工具查看如何分析程序运行时间和…...
什么是溶血症?什么是ABO溶血?溶血检查些什么?
什么是溶血症,什么是ABO溶血?女人是O型血,男人是其他血型的夫妻配对,最担心的是胎儿溶血症。从理论上讲,只要夫妻双方血型不同,母亲一定缺乏胎儿从父亲那里遗传的抗原。当任何人接触到他们缺乏的抗原时&…...

NLP实践——知识图谱问答模型FiD
NLP实践——知识图谱问答模型FiD0. 简介1. 模型结构2. 召回3. 问答4. 结合知识的问答0. 简介 好久没有更新了,今天介绍一个知识图谱问答(KBQA)模型,在此之前我一直在用huggingface的Pipeline中提供的QA模型,非常方便但…...

MyBatis 多表关联查询
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

《NFL橄榄球》:克利夫兰布朗·橄榄1号位
克利夫兰布朗(英语:Cleveland Browns)是一支职业美式橄榄球球队,位于俄亥俄州克利夫兰。 布朗隶属于美国全国橄榄球联盟(NFL)的北区,主场位于第一能源体育场。球队在1946年与AAFC联盟一同成立,并在1946年到…...
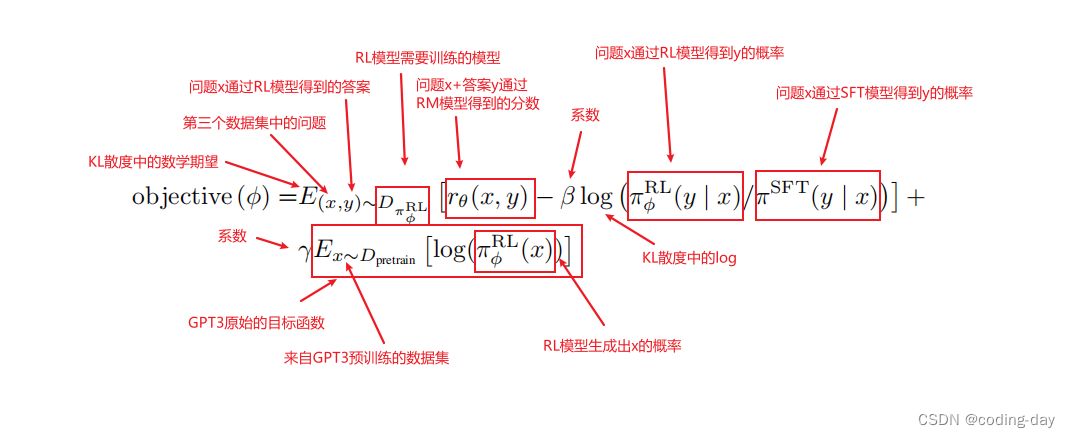
InstructGPT笔记
一、InstructGPT是在GPT3上微调,ChatGPT是在GPT3.5上微调 二、该论文展示了怎么样对语言模型和人类意图之间进行匹配,方法是在人类的反馈上进行微调。 **三、方法简介:**收集很多问题,使用标注工具将问题的答案写出来࿰…...

【uniapp】getOpenerEventChannel().once 接收参数无效的解决方案
uniapp项目开发跨平台应用常会遇到接收参数无效的问题,无法判断是哪里出错了,这里是讲替代的方案,现有三种方案可选。 原因 一般我们是这样处理向另一个页面传参,代码是这样写的 //... let { title, type, rank } args; uni.n…...
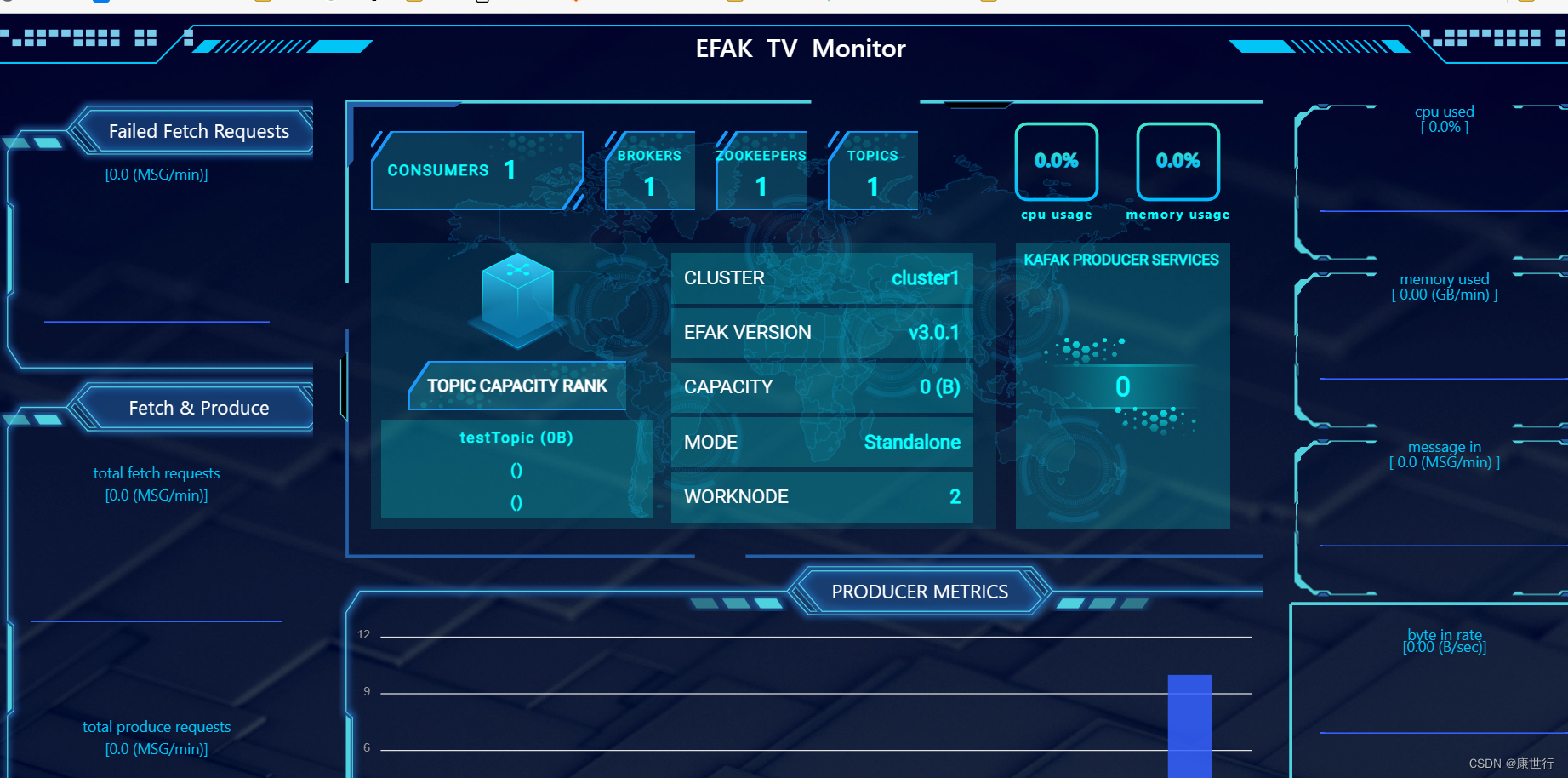
ELK分布式日志收集快速入门-(二)kafka进阶-快速安装可视化管理界面-(单节点部署)
目录安装前准备安装中安装成功安装前准备 安装kafka-参考博客 (10条消息) ELK分布式日志收集快速入门-(一)-kafka单体篇_康世行的博客-CSDN博客 安装zk 参考博客 (10条消息) 快速搭建-分布式远程调用框架搭建-dubbozookperspringboot demo 演示_康世行的…...

线程的创建
1. 多线程常用函数 1.1 创建一条新线程pthread_create 对此函数使用注意以下几点: 线程例程指的是:如果线程创建成功,则该线程会立即执行的函数。POSIX线程库的所有API对返回值的处理原则一致:成功返回0,失败返回错误…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

13.10 LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析
LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析 LanguageMentor 对话式训练系统架构与实现 关键词:多轮对话系统设计、场景化提示工程、情感识别优化、LangGraph 状态管理、Ollama 私有化部署 1. 对话训练系统技术架构 采用四层架构实现高扩展性的对话训练…...
