模糊的照片如何修复清晰?
相信有很多人用手机拍照时,觉得拍出来的照片一定是很漂亮的,结果拍了之后,拿出来一看模糊一片,根本看不清是什么。或者是只显示一半另一半模糊一片。而这些精彩瞬间很多时候是无法重拍的。虽然谁也不想拍出的照片出现模糊,但还是会发生在我们每一个人身上。那么模糊的照片如何修复清晰呢?
手机摄像头拍出来的照片清晰度和手机像素有很大关系。如果像素低,就是硬件性能问题,无法解决。也可能是手机平时不清理灰尘,所以拍出来的照片会模糊,是因为相机的镜头被灰尘覆盖了。把它清理干净。
而想要解决模糊的照片,不可避免就需要使用第三方图片修复软件。通过对模糊的照片进行细节填充,使其更清晰,提高照片质量,操作简单。接下来我来演示一下软件修复清晰度的方法。
1:添加损坏照片。首先,你可以在失易得官网上下载失易得图片修复软件并安装。安装完成后启动软件,先点击添加按钮将损坏的照片添加到软件。
2:修复过程。添加完照片后,点击页面右下方的蓝色“全部修复”按钮开始修复操作。
3:完成修复后,会弹出一个提示框,提醒你确认并预览。在所有照片都完成修复后。
4:点击“保存到本地”按钮,一次性将所有照片保存到指定路径,要注意不要将照片保存回原存储路径,防止文件破坏。
当然看我们也可以使用PS软件来修复图片:
打开PS,在软件界面打开要处理的模糊图片素材。用鼠标点击对应的图层,将复制的新图层命名为“图层复制”。
在软件界面第一栏显示的功能栏中找到滤镜,依次点击滤镜下的“锐化”-“USM”,调整数量半径、分辨率等其他参数。
找到右侧窗口中显示的图层属性,并相应地将“正常”属性设置为默认状态。设置成功后,可以看到清晰的画面。
以上就是关于模糊的照片如何修复清晰的方法,相信可以解决小伙伴们遇到的问题,希望小编带来的这篇文章能帮到大家。
相关文章:

模糊的照片如何修复清晰?
相信有很多人用手机拍照时,觉得拍出来的照片一定是很漂亮的,结果拍了之后,拿出来一看模糊一片,根本看不清是什么。或者是只显示一半另一半模糊一片。而这些精彩瞬间很多时候是无法重拍的。虽然谁也不想拍出的照片出现模糊…...

如何理解session、cookie、token的区别与联系?
session、cookie、token。 相信学过接口的朋友都特别熟悉了。 但是对我一个刚接触接口测试的小白来说,属实有点分不清楚。 下文就是我通过查阅各种资料总结出来的一点理解,不准确的地方还请各位指正。 (文末送洗浴中心流程指南)…...

【MyBatis】| MyBatis分页插件PageHelper
目录 一:MyBatis使⽤PageHelper 1. limit分⻚ 2. PageHelper插件 一:MyBatis使⽤PageHelper 1. limit分⻚ (1)概念: ①页码:pageNum(用户会发送请求,携带页码pageNum给服务器&am…...

Java枚举类详解
一、定义格式 public enum s { 枚举项1,枚举项2,枚举项3; } // 定义一个枚举类,用来表示春,夏,秋,冬这四个固定值 public enum Season {SPRING,SUMMER,AUTUMN,WINTER; } 二、枚举的特点 1、所有枚举类都是Enum的子类 2、我们可以通…...
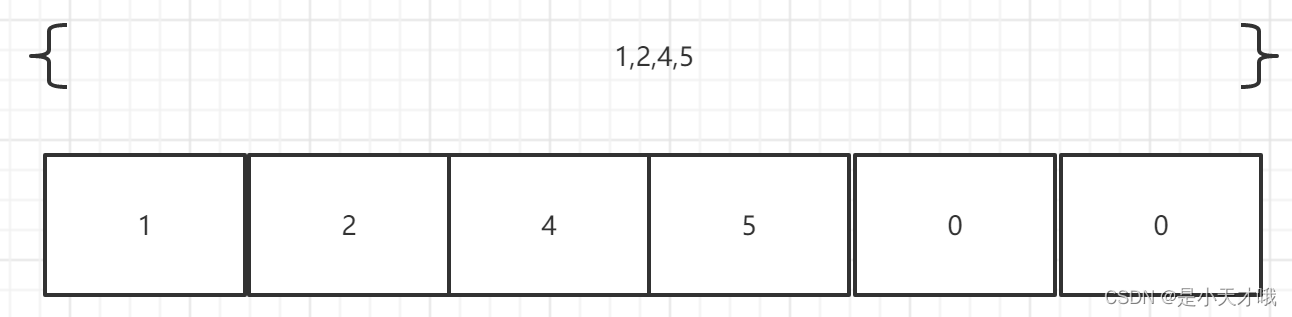
C语言数组
一.数组定义 数组由数据类型相同的一系列元素组成 如 int main(){ float candy[365]; char code[12]; int states[50]; … } cnady是包含了365个float元素的数组。code是包含了12个char类型的数组。states包含了50个int类型的数组。 二.数组初始化和取值 我们使用花括号包含值&…...
Scala 入门(第一章Scala 环境搭建、插件的安装)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 第 1 章 Scala 入门1.1 概述1.1.1 为什么学习 Scala1.1.2 Scala 发展历史1.1.3 Scala 和 Java 关系1.1.4 Scala 语言特点1.2 Scala 环境搭建1.3 Scala 插件安装1.4 HelloWorl…...

math@多项式@求和式乘法@代数学基本定理
文章目录多项式求和式乘法应用代数学基本定理相关证明高次方程其他关于多项式的参考多项式求和式乘法 S∏j1(∑k1ajk) j∏j1m(∑k1njajk) jS\prod_{j1}\left(\sum\limits_{k1}a_{jk}\right)_{\!\!\!j} \\\prod_{j1}^{m}\left(\sum\limits_{k1}^{n_j}a_{jk}\r…...

Kafka系列之:基于SCRAM和Ranger机制完成动态新增kafka读写账号、赋予账号对指定Topic的读写权限
Kafka系列之:基于SCRAM和Ranger机制完成动态新增kafka读写账号、赋予账号对指定Topic的读写权限 一、需求背景二、添加写用户三、查看用户是否添加到zookeeper中四、查看用户五、赋予用户topic写权限六、生产者配置文件七、ranger给用户权限八、往Topic写数据九、删除添加的用…...
——剪枝优化)
第五十三章 DFS进阶(一)——剪枝优化
第五十四章 DFS进阶(一)——剪枝优化一、什么是剪枝?二、剪枝优化的策略1、优化搜索顺序2、排除等效冗余3、可行性剪枝4、最优性剪枝5、记忆化搜索三、例题1、AcWing 165. 小猫爬山(DFS 剪枝优化)2、AcWing 167. 木棒…...
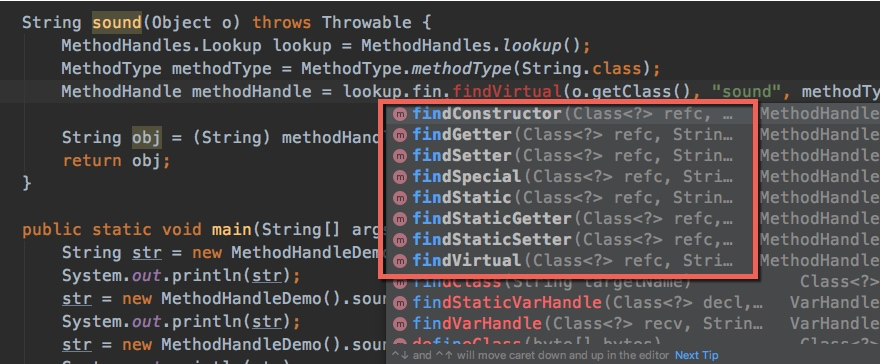
Java字节码深度知多少?
文章目录1、字节码结构1.1、基本结构1.2、实际观测2、内存表示3、方法调用指令4、invokedynamicEND结语Java真的是长盛不衰,拥有顽强的生命力。其中,字节码机制功不可没。字节码,就像是 Linux 的 ELF。有了它,JVM直接摇身一变&…...

【C++】智能指针(万字详解)
🌈欢迎来到C专栏~~智能指针 (꒪ꇴ꒪(꒪ꇴ꒪ )🐣,我是Scort目前状态:大三非科班啃C中🌍博客主页:张小姐的猫~江湖背景快上车🚘,握好方向盘跟我有一起打天下嘞!送给自己的一句鸡汤&…...
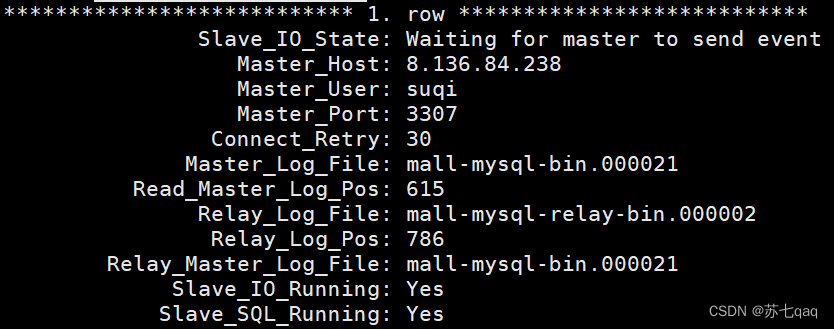
使用docker配置mysql主从复制
1.新建主服务器容器实例: docker run -p 3307:3306 --name mysql \ -v /docker/mysql/data:/var/lib/mysql \ -v /docker/mysql/conf:/etc/mysql/conf \ -v /docker/mysql/log:/var/log/mysql \ -e MYSQL_ROOT_PASSWORDroot \ -d mysql:5.7 设置容器卷之后…...

v3 异步组件及分包使用
1 app.vue <template> <!-- vue3异步组件必须使用suspense --> <Suspense> <template #default> <!-- 异步组件 --> <SyncVue></SyncVue> </template> <template v-slot:fallback> <!-- 优先显示骨架屏 --> <…...

实用调试技巧【上篇】
🔴本文章是在 Visual Studio 2022(VS2022)编译环境下进行操作讲解 文章目录🥳1. 什么是bug?🥳2.调试有多重要?2.1. 我们是如何写代码的?2.2.调试是什么?2.3.调试的基本步…...

JavaScript 教程
手册简介JavaScript 是世界上最流行的脚本语言。 JavaScript 是属于 web 的语言,它适用于 PC、笔记本电脑、平板电脑和移动电话。 JavaScript 被设计为向 HTML 页面增加交互性。 许多 HTML 开发者都不是程序员,但是 JavaScript 却拥有非常简单的语法。几…...

在SpringBoot里面使用原生的Servlet
在SpringBoot里面使用Servlet 首先在主程序中添加注解主程序添加ServletComponentScan // 加上这个注解之后就可以使用原生的组件了 HttpServlet 继承HttpServlet 重写方法 添加WebServlet 第一种方式使用注解 WebServlet(value "/helsk") public class HelloSe…...

商标被驳回,先别慌!挽回商标有办法
商标注册是一个漫长的等待过程,提交了注册申请之后不代表就能得心应手。商标局在接收到申请后,便会开始各阶段审查,面对不符合条件的商标会予以商标驳回。商标局基于什么原因而驳回注册申请呢?驳回后还有必要进行商标驳回复审吗?今天心周企…...
VMware安装Linux虚拟机后忘记root密码处理方法
OS版本:Red Hat 7.7 问题说明: 之前用VMWare安装了一台Linux虚机,由于长期没使用,导致忘记了root密码。所以需要修改root密码。 Root密码修改 现将修改root密码的操作步骤记录如下。 1.启动虚拟机,出现启动倒计时…...
Centos安装OpenResty
文章目录一. OpenResty是什么二. OpenResty的安装1. 安装开发库2. 安装OpenResty仓库3. 安装OpenResty4. 安装opm工具5. 目录结构6. 配置nginx的环境变量7. 启动和运行8. 配置文件修改三. 小案例1. 案例说明2. OpenResty监听请求3. 编写业务代码4. 获取请求参数一. OpenResty是…...
阿里云部署SpringBoot项目
目录 步骤1:购买服务器(新用户免费试用一个月) 步骤2:查看服务器相关信息 编辑 步骤3:设置安全组 步骤4:远程连接 步骤5:使用FinalShell连接阿里云服务器 步骤6:阿里云服务器上安装JDK 编辑 步骤7…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
