CSDN每日一练:小豚鼠搬家
题目名称:小豚鼠搬家
时间限制:1000ms内存限制:256M
题目描述
小豚鼠排排坐。 小艺酱买了一排排格子的小房子n*m,她想让k只小豚鼠每只小豚鼠都有自己的房子。 但是为了不浪费空间,她想要小房子的最外圈尽量每行每列都有一只小豚鼠居住。 小艺酱想知道自己有多少种方案安排小豚鼠。
输入描述:
输入整数n,m,k。(1<=n,m<=20,0<=k<=n*m)
输出描述:
输出方案数,答案对1e9+7取模。
示例
示例1
输入
3 3 2
输出
2
提示
无
用例里有两个比较特殊,一个是没有豚鼠的用例,[3, 4, 0],这个如果用递归的话,需要避免这个用例,豚鼠数字小于2,就返回0,笼子就1个格,返回1
另一个就是真正的算法考验的用例了 [5, 5, 12],返回结果是 4704606…我在本地跑了一下,最土的递归用了一分半钟左右才得出这个结果
先放第一版的
def s(row,col,num,start,pos):#result = []result = 0if num == 1:for i in range(start,row*col):t = pos + [i]if len([_ for _ in t if _ // col == 0])>0 and len([_ for _ in t if _ % col == 0])>0 and len([_ for _ in t if _ // col == row-1])>0 and len([_ for _ in t if _ % col == col - 1])>0:#result.append(pos + [i])result += 1return resultelse:for i in range(start,row*col-num+1):result += s(row,col,num-1,i+1,pos+[i])return resultn,m,k = [4,4,14]
result = s(n,m,k,0,[])
于是就想起来,好像看到过某个文章里讲解了这个题目怎么算,完全不用递归组合什么的,就是数学公式,最后找了半天也没找到之前看到的文章,但还是搜索出了一个类似的,讲解的也比较清楚的文章
https://www.cnblogs.com/pengwill/p/7367030.html
文章的意思就是用最大组合减去不合要求的组合,再加上遗漏的组合,再减去遗漏组合中不合要求的组合。。。嗯,用循环完成的,叫什么容斥原理。。。原谅老顾没上过学。。。。
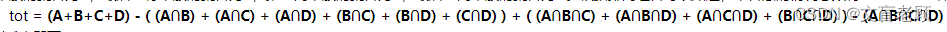
具体为什么程序这么写倒是没搞明白,尤其是中间用到位运算,怎么就和这总计的16项(最大集合,及15个容斥原理对应内容)
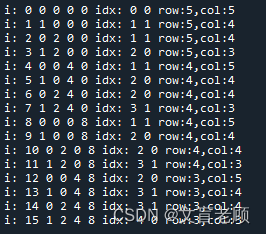
最后还是列了个输出信息才弄明白,哪些是加的,哪些是减的,分别加了多少减了多少。。。。嗯,只需要一个阶乘函数,一个组合函数就够了
n,m,k = [5,5,12]total = 0for i in range(16):idx = 0row = ncol = mif i & 1: # 对应集合 A,最上边一行无小鼠col -= 1idx += 1if i & 2: # 对应集合 B,最下边一行无小鼠col -= 1idx += 1if i & 4: # 对应集合 C,最左边一列无小鼠row -= 1idx += 1if i & 8: # 对应集合 D,最右边一列无小鼠row -= 1idx += 1print('i:',i,i&1,i&2,i&4,i&8,'idx:',idx,idx & 1,'row:{},col:{}'.format(row,col))if idx & 1:total -= int(X(row*col,k))else:total += int(X(row*col,k))print(total)准备自己时常复习一下,争取把这个公式弄明白,加油,老顾
弄这么个文章,主要是搜不到“小豚鼠搬家”这个题目的题解,百度出来的,都没有具体算法,好伤心
相关文章:

CSDN每日一练:小豚鼠搬家
题目名称:小豚鼠搬家 时间限制:1000ms内存限制:256M 题目描述 小豚鼠排排坐。 小艺酱买了一排排格子的小房子n*m,她想让k只小豚鼠每只小豚鼠都有自己的房子。 但是为了不浪费空间,她想要小房子的最外圈尽量每行每列都有…...

Dockerfile命令及实践构建一个网站
dockerfile用于构建docker镜像的,部署一个用于运行你所需的容器环境。相当一个脚本,通过dockerfile自己的指令,来构建软件依赖、文件依赖、存储、定制docker镜像的方式有两种:手动修改容器内容,导出新的镜像基于Docker…...
[VMware]Ubuntu18.04 网络图标消失
Ubuntu 18.04 网络图标消失运行环境问题解决NO.1 执行 sudo systemctl stop network-managerNO.2 执行 sudo rm /var/lib/NetworkManager/NetworkManager.stateNO.3 执行 sudo systemctl start network-managerNO.4 vi /etc/NetworkManager/NetworkManager.confNO.5 执行 sudo …...

国产C2000,P2P替代TMS320F280049C,独立双核32位CPU,主频高达400MHz
一、特性参数 1、独立双核,32位CPU,单核主频400MHz 2、IEEE 754 单精度浮点单元 (FPU) 3、三角函数单元 (TMU) 4、1MB 的 FLASH (ECC保护) 5、1MB 的 SRAM (ECC保护&…...

二十五、Gtk4-多线程分析
1 回顾 1.1 Gnome相关 首先回顾一下GLib,GObject,GIO,Gtk的不同,因为下面会涉及到这些概念里面的函数。 所有这些都是由Gnome项目开发的库,一般都用于Gnome环境相关的应用程序。 Gtk:GUI界面库。GLib&a…...
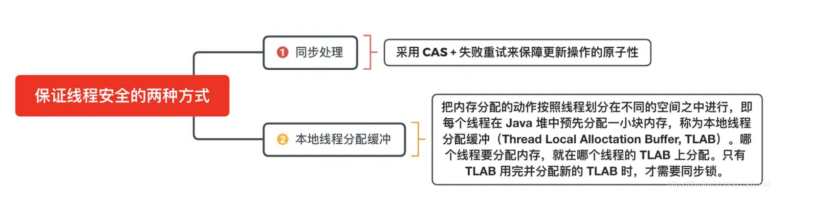
JVM基础学习
JVM分为两个子系统,两个组件一个子系统是Class loader类装载系统,另一个子系统是Execution Engine执行引擎一个组件是Runtime data area 运行时数据区,Native Interface 本地接口Class loader:根据给定的全限定类名来装载class文件到运行时数…...

ASML逆袭史:人、资金、技术,缺一不可
前言 近年来,由于众所周知的原因,荷兰ASML(阿斯麦)公司的先进半导体制造设备——光刻机,进入普通大众视野,成为人们茶余饭后谈论的焦点话题之一。 1月底,“美日荷三方谈判达成协议,可…...
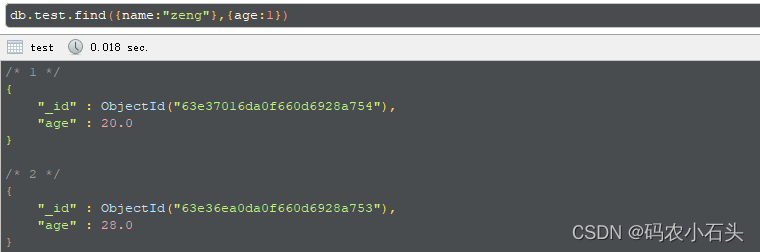
MongoDB 覆盖索引查询
MongoDB 覆盖索引查询 官方的MongoDB的文档中对覆盖查询做了说明: 所有的查询字段是索引的一部分所有的查询返回字段在同一个索引中 由于所有出现在查询中的字段是索引的一部分, MongoDB 无需在整个数据文档中检索匹配查询条件和返回使用相同索引的查询…...
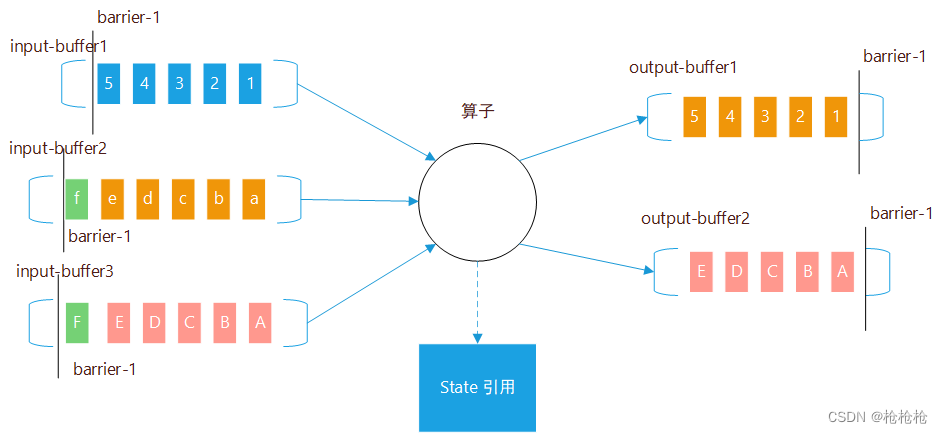
Flink Checkpoint 中的Aligned Checkpoint 和 Unaligned Checkpoint
文章目录知识点反压CheckpointBarrierAligned CheckpointUnaligned Checkpoint核心思想实现原理UC同步阶段UC异步阶段知识点 反压 反压是流式系统中关于处理能力的动态反馈机制,并且是从下游到上游的反馈,一般是在实时数据处理的过程中,上游…...

C++快速入门
本章内容我将结合C语言一起,初步学习了解c,与大家一起快速入门这门语言。当然鉴于c本身属于一门中级语言,大家对编程有一定了解之后来学习这门知识会更加得心应手。简介C 被认为是一种中级语言,它综合了高级语言和低级语言的特点。…...

ubuntu18.04 network有线网络图标缺失解决记录
先按照博客1安装驱动 博客1链接:Ubuntu安装 Realtek R8125 驱动_Lwang2018的博客-CSDN博客_瑞昱8125 for ubunt 安装完成后,遇到问题:ifconfig -a显示的有线网接口(名字以en开头)没有ip地址…...
java对象克隆和面向对象的设计原则
java进阶注解内置注解元注解自定义注解对象克隆浅克隆深克隆java设计模式建模语言类之间的关系依赖关系关联关系单向关联双向关联自关联聚合关系组合关系继承关系实现关系面向对象设计原则单一职责开闭原则里氏替换原则依赖倒置接口隔离迪米特原则组合/聚合复用原则注解 java注…...

传透式血氧仪设计方案
该方案一种检测方式是选择使用光敏二极管接收光信号,采用传统穿透式夹指测量;另一种是使用光谱传感器接收光信号,采用反射式测量。该传感器可将光信号直接转换成数据信息给主控端进行处理,从而节省了用户将光信号转换成模拟信号&a…...
让逆向工程师们头疼的代码混淆,就像永远也走不出的“浪浪山”
目录 代码混淆究竟是什么? 如何做代码混淆? 代码混淆不等于加密 App 加固非一时之功 “我想离开浪浪山。” 在数次尝试破解某个App 时,某个逆向工程师无奈感慨道。 逆向工程师顾名思义就是把一个个完整的软件逆推,还原成一段段…...
——心脏病数据集补充)
【拓展】基于机器学习的心脏病预测方法(14)——心脏病数据集补充
目录 前言1、数据集11.1 数据集介绍1.2 数据集属性2、数据集22.1 数据集介绍2.2 数据集属性3、数据集33.1 数据集介绍3.2 数据集属性4、下载地址前言 在实际研究过程中,前文所述数据集由于尺寸过小(仅有303份数据和13个属性信息)或数据集单一(仅有一个数据集,不具备普适性…...

深度解读Webpack中的loader原理
一、前言 webpack 是一个现代 JavaScript 应用的静态模块打包器。那么 webpack 是怎样实现不同种类资源模块加载的呢? 没错就是通过 loader。loader 用于对模块的源代码进行转换。loader 可以使你在 import 或加载模块时预处理文件。 我们带着下面几个问题&#…...

2023年全国最新二级建造师精选真题及答案
百分百题库提供二级建造师考试试题、二建考试预测题、二级建造师考试真题、二建证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 一、单选题 1.关于法人在建设工程中的地位的说法,正确的是(࿰…...

为什么现代企业发展离不开CRM系统的助力
如今的CRM系统对于任何企业来说都重要,因为它能帮助企业收获新客户,保留现有客户,并且将不同部门的信息全部汇集,实时提供关于每位客户整体全面的看法。因此,销售、市场营销和客户支持等领域的客户直接服务员工能够做出…...
-获取农历和天气)
vb.net计算之.net core基础(1)-获取农历和天气
目录 .net core 简介创建hello,world应用程序获取天气和农历.net core 简介 .NET Core是适用于 Windows、Linux 和 macOS 的免费、开源托管的计算机软件框架。 它是微软开发的第一个官方版本,具有跨平台能力的应用程序开发框架 (Application Framework),未来也将会支持 Free…...
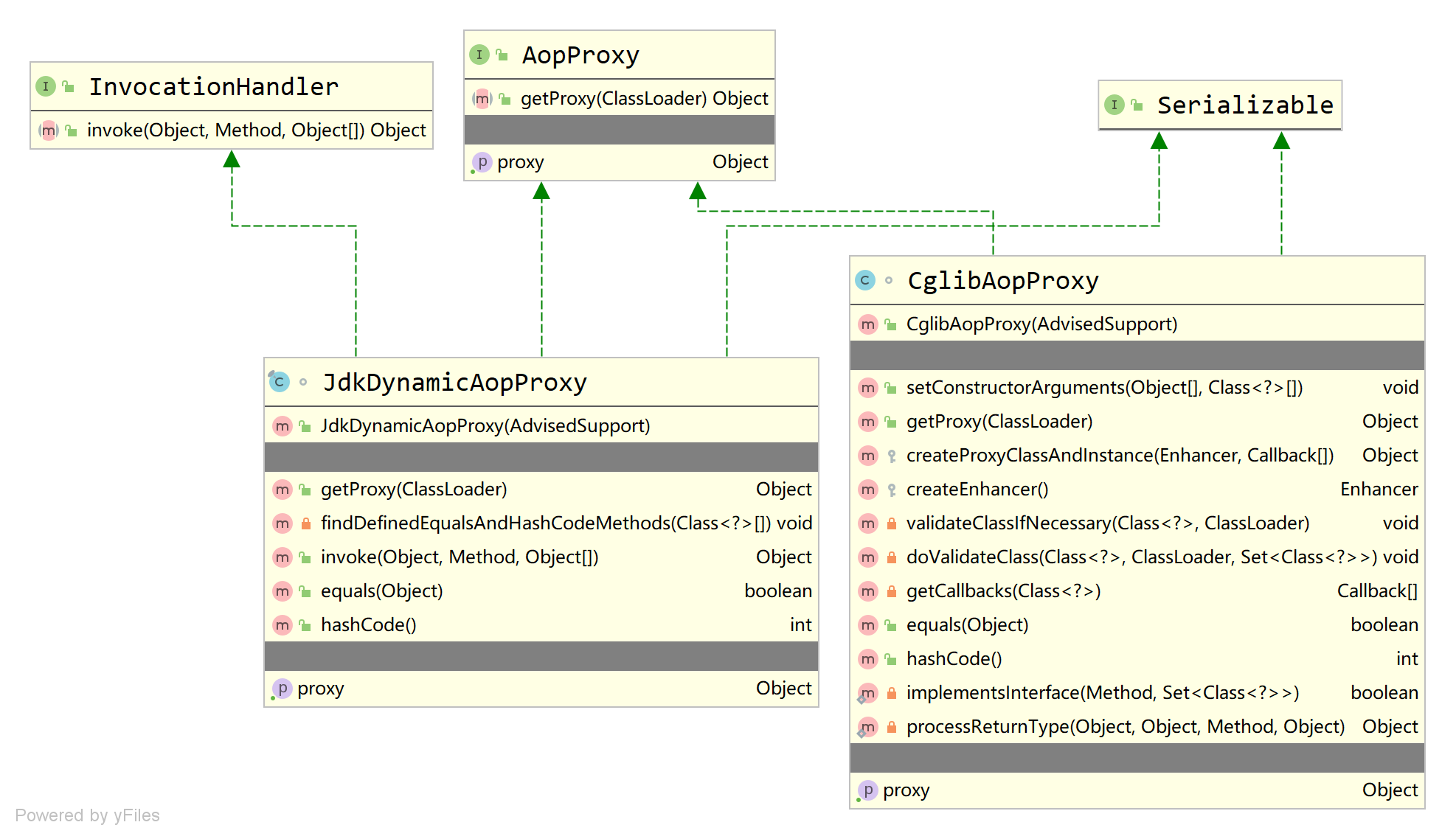
设计模式之代理模式详解和应用
目录1 代理模式定义2 代理模式的应用场景3 代理模式的通用写法4 从静态代理到动态代理5 静态模式在业务中的应用6 动态代理在业务中的应用7 手写JDK动态代理实现原理7.1 JDK动态代理的实现原理7.2 CGLib动态代理容易踩的坑8 CGLib代理调用API及原理分析9 CGLib和JDK动态代理对比…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
