【代码随想录训练营】【Day15】第六章|二叉树|层序遍历|226.翻转二叉树|101.对称二叉树
层序遍历
题目详细:LeetCode.102
层序遍历与上一节讲的三种遍历方式有所不同,层序遍历是指按从上到下,从左到右的顺序,逐层地遍历二叉树的节点。
从其节点的遍历顺序上观察,我们可以发现其跟广度优先遍历(BFS)的遍历思想非常相似,既然我们可以利用队列先进先出的特点来实现广度优先遍历,那么我们也可以用队列来实现对二叉树的层序遍历:
- 定义一个二维数组,其下标表示第i层,数组元素则存储着每一层遍历的节点
- 定义一个队列,利用其先进先出的特点,先将非空的根节点进队
- 定义一个循环,遍历入队的二叉树节点
- 定义一个变量,记录每一层的节点数目,也就是当前队列的长度
- 定义一个循环,获取变量得知在第一层,只有根节点一个节点
- 那么我们只需要出队一次,将根节点出队,队列长度 - 1
- 定义一个一维数组存放该层的节点值,并将该数组追加入到二维数组中
- 然后将其非空的左右节点依次进队
- 循环直到该层的节点都遍历完毕
- 循环直到队列为空,说明二叉树层序遍历完成
Java解法(队列,BFS):
class Solution {public List<List<Integer>> ans = new ArrayList<>();public List<List<Integer>> levelOrder(TreeNode root) {this.bfs(root);return ans;}public void bfs(TreeNode root){Queue<TreeNode> queue = new LinkedList<>();if(null != root) queue.offer(root);while(!queue.isEmpty()){int n = queue.size();List<Integer> floor = new ArrayList<>();while(n-- > 0){TreeNode node = queue.poll();floor.add(node.val);if(null != node.left) queue.offer(node.left);if(null != node.right) queue.offer(node.right);}ans.add(floor);}}
}
这道题我们可以模拟层序遍历的思想,利用递归来解题,只需要在递归函数中增加一个变量,记录节点是第几层的即可:
Java解法(模拟,递归):
class Solution {public List<List<Integer>> ans = new ArrayList<>();public List<List<Integer>> levelOrder(TreeNode root) {this.order(root, 0);return ans;}public void order(TreeNode root, int level){if(null == root) return;if(level > ans.size() - 1){List<Integer> floor = new ArrayList<>();floor.add(root.val);ans.add(floor);}else{ans.get(level).add(root.val);}this.order(root.left, level + 1); this.order(root.right, level + 1); }
}
学会了二叉树的层序遍历后,可以一口气打完以下十道LeetCode题:
102.二叉树的层序遍历
104.二叉树的最大深度
107.二叉树的层次遍历II
111.二叉树的最小深度
116.填充每个节点的下一个右侧节点指针
117.填充每个节点的下一个右侧节点指针II
199.二叉树的右视图
429.N叉树的层序遍历
515.在每个树行中找最大值
637.二叉树的层平均值
翻转二叉树
题目详细:LeetCode.226
翻转二叉树的过程和结果:

观察上图动画我们可以发现,上图采用的是层序遍历的顺序,在遍历的过程中,将每个节点的左右节点进行交换,这就是翻转二叉树的解题思想。
所以想要解题很简单,就是采用合适的遍历方法,在访问节点的时候,将其左右节点进行交换即可;
需要注意的是,在这道题中我们采用的遍历二叉树方法一般是:前序遍历、后序遍历和层序遍历,因为采用中序遍历的方式会导致重复交换子节点,需要在遍历过程中加以逻辑判断才能避免这一情况,不易编写和理解。
如何遍历在这里就不作赘述了,不了解的可以查看上一节的内容,详细讲述了遍历二叉树的各种方法:【Day14】传送门
Java解题(递归,前序遍历):
class Solution {public TreeNode invertTree(TreeNode root) {this.invertPre(root);return root;}public void swapChildNode(TreeNode node){TreeNode temp = node.left;node.left = node.right;node.right = temp;}public void invertPre(TreeNode root){if(null == root) return;this.swapChildNode(root);this.invertPre(root.left);this.invertPre(root.right);}
}
Java解题(统一迭代,前序遍历):
class Solution {public TreeNode invertTree(TreeNode root) {this.invertPre(root);return root;}public void swapChildNode(TreeNode node){TreeNode temp = node.left;node.left = node.right;node.right = temp;}public void invertPre(TreeNode root){Stack<TreeNode> stack = new Stack<>();if(null != root) stack.push(root);while(!stack.isEmpty()){// 标记节点TreeNode tagNode = stack.peek();if(tagNode != null){// 非标记节点,先弹出,在需要处理的节点后追加空指针作为标记(仅作标记,不作处理)TreeNode node = stack.pop();if(null != node.right) stack.push(node.right);if(null != node.left) stack.push(node.left);stack.push(node);stack.push(null);}else{// 遇到标记节点,先弹出作为标记的空指针的节点,再处理数据(处理节点,不作标记)stack.pop();TreeNode node = stack.pop();this.swapChildNode(node);}}}
}
对称二叉树
题目详细:LeetCode.101
由题可知,判断一棵二叉树是否对称:
- 根节点无需比较
- 接着比较树的内侧的节点和外侧的节点,而不是比较树的左右节点
- 当每棵子树都满足内侧节点相等,外侧节点相等,那么则称这整棵二叉树是对称的
所以关键在于如何遍历二叉树,以及如何比较树的内侧节点和外侧节点。
既然根节点不需要比较,那么我们就需要同时比较其左右两棵子树上的节点,在比较过程中,会出现四种情况:
- 左右节点皆为空,则是对称的
- 左右节点只有一个为空,则是不对称的
- 左右节点皆不为空,但是他们的值不相等,是不对称的
- 左右节点皆不为空,但是他们的值相等,是对称的
所以对于每一棵子树,我们只需要按照上述情况去比较其内侧和外侧节点,就可以得到正确答案:
- 树的
内侧节点选左子树的右节点和右子树的左节点进行比较 - 树的
外侧节点选左子树的左节点和右子树的右节点进行比较 - 当出现一种不对称情况时,则整个树是不对称的,无需继续比较
- 当出现对称情况时,继续比较剩余的左右子树
Java解题(递归):
class Solution {public boolean isSymmetric(TreeNode root) {return this.check(root.left, root.right);}public boolean check(TreeNode leftNode, TreeNode rightNode){if(null == leftNode && null == rightNode) return true;else if(null == leftNode || null == rightNode || leftNode.val != rightNode.val) return false;return check(leftNode.right, rightNode.left) && check(leftNode.left, rightNode.right);}
}
Java解题(迭代,队列):
class Solution {public Queue<TreeNode> queue = new LinkedList<>();public boolean isSymmetric(TreeNode root) {return this.check(root.left, root.right);}public boolean check(TreeNode leftNode, TreeNode rightNode){this.queue.offer(leftNode);this.queue.offer(rightNode);while(!queue.isEmpty()){leftNode = queue.poll();rightNode = queue.poll();if(null == leftNode && null == rightNode)continue;else if(null == leftNode || null == rightNode || leftNode.val != rightNode.val){return false; this.queue.offer(leftNode.right);this.queue.offer(rightNode.left);this.queue.offer(leftNode.left);this.queue.offer(rightNode.right);}return true;}
}
观察代码以及二叉树的遍历过程,我们也可以发现,对于对称二叉树的遍历顺序,左子树的遍历顺序是右左根,而右子树的遍历顺序是左右根,两者都属于后序遍历,也就是说,这道题是基于后序遍历来解决的。
除了在二叉树中常用的递归方法外,我们还可以结合前面学习的其他数据结构,如栈和队列,也能够辅助我们遍历和处理二叉树。
最后这两天做二叉树相关的题目之后,给我的感触就是,二叉树的题目千变万化,但是总结起来就是两个要点:选择最佳的遍历顺序 + 处理节点的需求逻辑,可见解答二叉树相关的题目时,理解和掌握二叉树不同的遍历思想是尤其重要的:
水之积也不厚,则其负大舟也无力。
相关文章:

【代码随想录训练营】【Day15】第六章|二叉树|层序遍历|226.翻转二叉树|101.对称二叉树
层序遍历 题目详细:LeetCode.102 层序遍历与上一节讲的三种遍历方式有所不同,层序遍历是指按从上到下,从左到右的顺序,逐层地遍历二叉树的节点。 从其节点的遍历顺序上观察,我们可以发现其跟广度优先遍历࿰…...
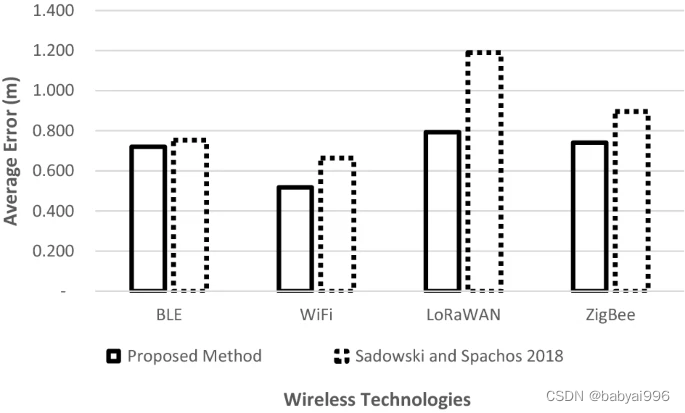
基于圆展开自适应三边测量算法的室内定位
基于圆展开自适应三边测量算法的室内定位 具有无线通信功能的移动设备的日益普及刺激了室内定位服务的增长。室内定位用于实时定位设备位置,方便访问。然而,由于大量障碍物,与室外定位相比,室内定位具有挑战性。全球定位系统非常适…...

使用中断子系统实现对LED灯的控制
中断顶半部:不允许耗时操作 代码流程: 1、基于字符设备驱动的注册(手动/自动) 2、基于设备树文件的自定义完成(myled, myirq) 2、基于GPIO子系统实现led的点亮(流水/测试文件控制) 3、中断子系统操作流程 …...
《爆肝整理》保姆级系列教程python接口自动化(十五)--参数关联接口(详解)
简介 我们用自动化新建任务之后,要想接着对这个新建任务操作,那就需要用参数关联了,新建任务之后会有一个任务的Jenkins-Crumb,获取到这个Jenkins-Crumb,就可以通过传这个任务Jenkins-Crumb继续操作这个新建的任务。 …...

【JDK8】MyBatis源码导入Idea
1.背景 为了更好的将MyBatis的开发设计思想带到日常开发工作,将MyBatis源码导入到本地开发工具中(idea)。我自己在导入的时候碰到几个问题,耽误了自己一点时间,这里我把它们记下来,后边的小伙伴可不要踩我的坑。 Java版本&#x…...
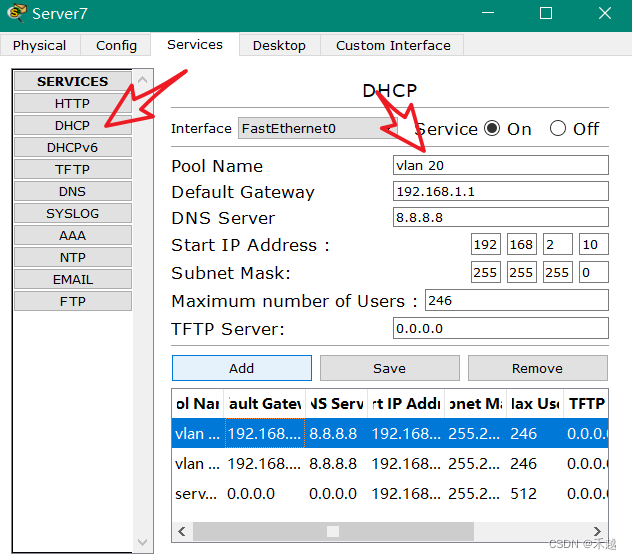
三层交换机DHCP中继
关于中继,我们需要有一个对比。正常情况下我们是不是需要配置单臂路由然后开启DHCP地址池,然就设置网段网关以及DNS。这样的话考验 的其实是命令功底。但是为了方便,我们 可以添加服务器,将这个服务给到服务器去配置,这…...
C++之RALL机制
RALL是Resource acquisition is initialization的缩写,意思是“资源获取即初始化”,其核心思想是利用C对象生命周期的概念来控制程序的资源。它的技术原理很简单,如果希望对某个重要资源进行跟踪,那么创建一个对象,并将…...
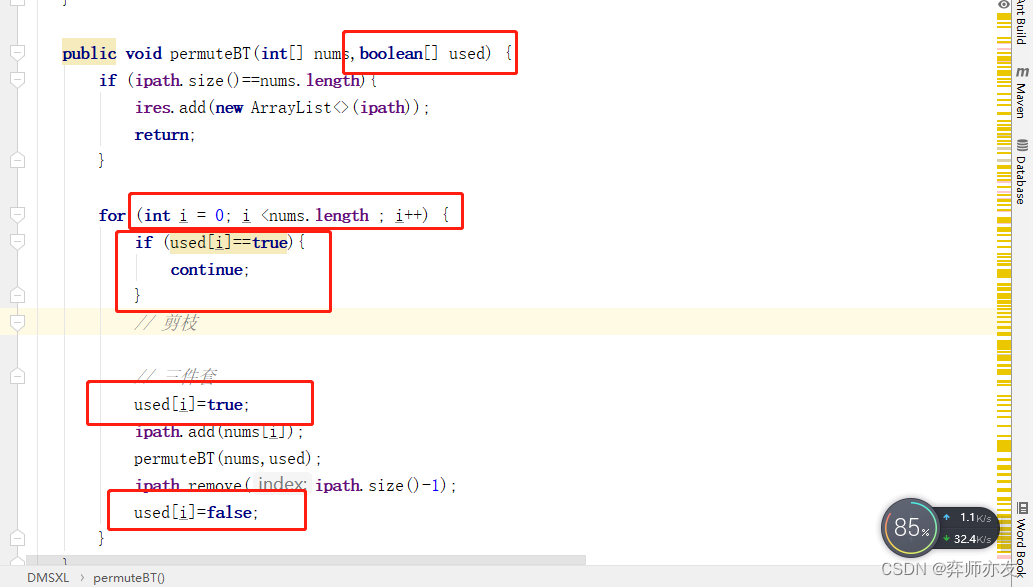
回溯算法章末总结
组合问题的特点 (1)abba 选中a之后,就不再选了 (2)找出所有的组合 (长度可以不相等) 组合问题模板 做回溯题步骤 (0)判断问题类型 (1)树状图 …...

【SpringBoot】为异步任务规划线程池
一、线程池的作用 防止资源占用无限的扩张调用过程省去资源的创建和销毁所占用的时间 在上一节中,我们的一个异步任务打开了一个线程,完成后销毁。在高并发环境下,不断的分配新资源,可能导致系统资源耗尽。所以为了避免这个问题…...
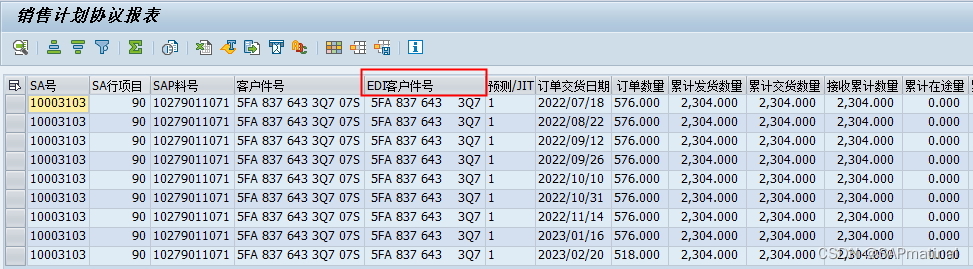
SAP ABAP 输出结果带有空格
方法一: 字段内容前增加空格,需使用全角空格,使用半角空格时,ALV显示无效,空格无法显示, 全角与半角的切换方法:shift空格切换, 如下的标记部分,要想通过ALV显示空格&…...

Opengl ES之踩坑记
前因 最近在尝试使用Opengl ES实现一些LUT滤镜效果,在实现这些滤镜效果的时候遇到一些兼容性的坑,踩过这些坑后我希望把这几个坑分享给读者朋友们, 希望同在学习Opengl ES的朋友们能少走弯路。 关于LUT滤镜相关的介绍,也是这个O…...
设计模式第六讲:责任链模式和迭代器模式详解
一. 责任链模式1. 背景在现实生活中,常常会出现这样的事例:一个请求有多个对象可以处理,但每个对象的处理条件或权限不同。例如,公司员工请假,可批假的领导有部门负责人、副总经理、总经理等,但每个领导能批…...
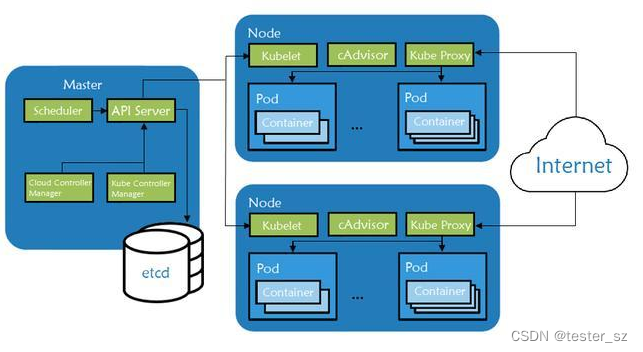
K8s 架构简介(一)
一、前言 在开始学习K8s之前,让我们对容器有一个基本的了解 1.1 什么是容器 一个容器镜像是一个可运行的软件包,其中包含了一个完整的可执行程序,包括代码和运行时需要应用、系统库和全部重要设置的默认值。 通过将应用程序本身ÿ…...
xshell6运行报错:由于找不到mfc110u.dll、MSVCR110.dll无法继续执行代码
今天给大家分享一下我刚装完系统遇到得问题,由于新盟的罗建雨【胡巴】老师帮我给电脑加了固态,又重装了系统,因此电脑里面得所有软件需要重装,在我重装的过程中遇到了一个小问题给大家分享一下,如果大家以后遇到也方便解决。 问题: 安装Xshell时电脑系统报错:“由于找…...
Baklib知识库管理平台,协助组织提升知识管理水平
随着信息时代和知识经济时代的到来,企业内部信息资料繁多冗杂,知识管理逐渐成为各大企业的重要工作之一,企业管理者无不感受到巨大的压力,怎么样将知识进行有效的管理,成为一个难点,并且随着信息不断的更迭…...
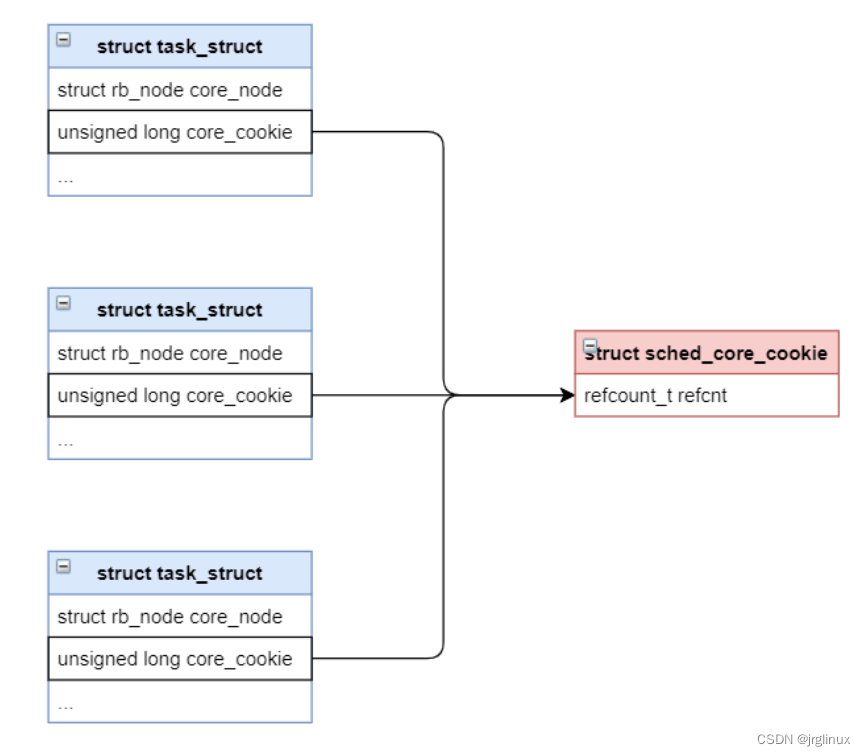
一文搞懂core-scheduling核心机制
cookie的原理借助于unsigned long型,和refcount_t引用计数器。 32位64位char *4字节8字节unsigned long4字节8字节 数据结构修改 首先看看实现core scheduling功能对数据结构有哪些修改 task_struct struct task_struct{struct rb_node core_node;unsigned long…...

IP地址在金融行业有哪些应用?
中国加入WTO以来经济得到迅速发展,金融行业随着经济发展体系越来越完善。随着西方金融公司和理念的加入中国金融行业开始多样化发展。金融行业在快速发展的同时也引发了许多弊端。如何维护挖掘客户更大需求?如何获取更多优质客户?如何提升网络…...
GT-suite v2016解决许可证过期问题(附新版liscense下载地址)
安装GT-suite v2016时遇到了如图报错的问题。当时的报错找不到了,下图是贴吧相同问题的报错图。 为了解决问题,先根据某网友的如下答复操作: 添加环境变量后仍然有相同报错。 看来需要寻找其他方法。 再尝试着卸载GT-suite v2016,…...

小红书商业笔记与普通笔记区别是什么?小红书笔记有哪几种
主攻单一平台,如何迅速打造爆文。针对软文发布类别的选择,小红书商业笔记与普通笔记区别究竟是什么,今天为大家带来的详细分析,告诉你该如何用最少的成本,做出“爆文”。1、小红书的笔记类型我们都知道,小红…...
DataWhale-统计学习方法打卡Task01
学习教材《统计学习方法(第二版)》李航 统计学习方法(第2版) by...李航 (z-lib.org).pdf https://www.aliyundrive.com/s/maJZ6M9hrTe 点击链接保存,或者复制本段内容,打开「阿里云盘」APP ,无…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...
