算法刷题打卡第91天:统计一个圆中点的数目
统计一个圆中点的数目
难度:中等
给你一个数组 points ,其中 points[i] = [xi, yi] ,表示第 i 个点在二维平面上的坐标。多个点可能会有 相同 的坐标。
同时给你一个数组 queries ,其中 queries[j] = [xj, yj, rj] ,表示一个圆心在 (xj, yj) 且半径为 rj 的圆。
对于每一个查询 queries[j] ,计算在第 j 个圆 内 点的数目。如果一个点在圆的 边界上 ,我们同样认为它在圆 内 。
请你返回一个数组 answer ,其中 answer[j] 是第 j 个查询的答案。
示例 1:
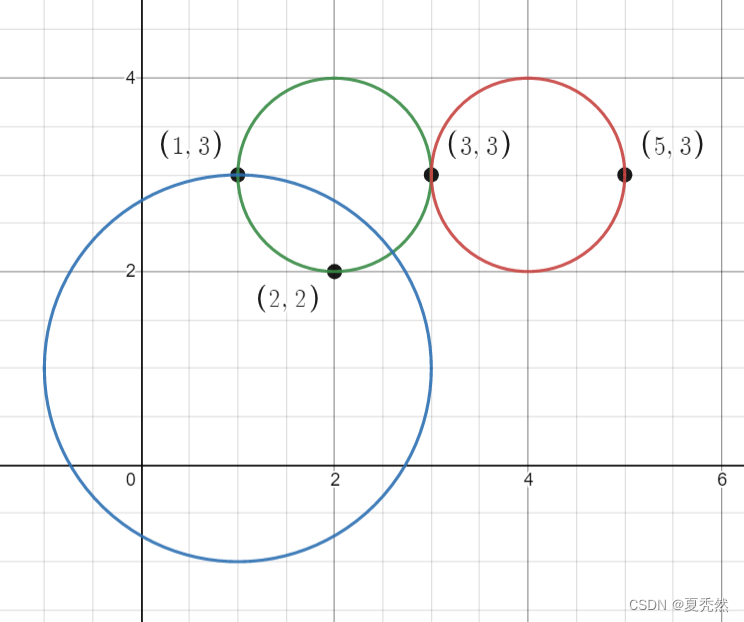
输入:points = [[1,3],[3,3],[5,3],[2,2]], queries = [[2,3,1],[4,3,1],[1,1,2]]
输出:[3,2,2]
解释:所有的点和圆如上图所示。
queries[0] 是绿色的圆,queries[1] 是红色的圆,queries[2] 是蓝色的圆。
示例 2:
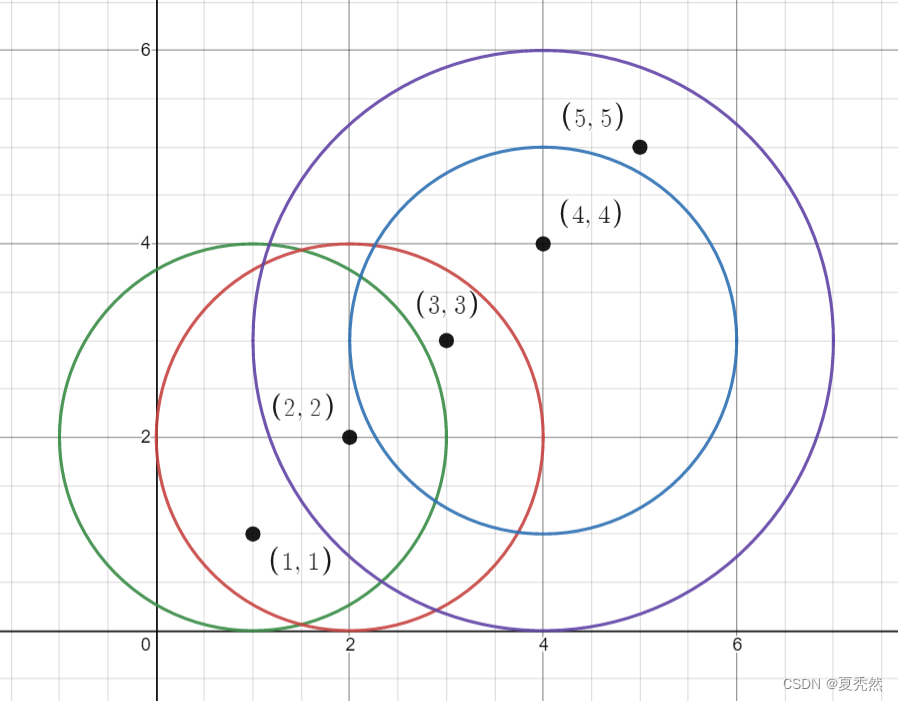
输入:points = [[1,1],[2,2],[3,3],[4,4],[5,5]], queries = [[1,2,2],[2,2,2],[4,3,2],[4,3,3]]
输出:[2,3,2,4]
解释:所有的点和圆如上图所示。
queries[0] 是绿色的圆,queries[1] 是红色的圆,queries[2] 是蓝色的圆,queries[3] 是紫色的圆。
枚举每个点是否在每个圆中
思路:
我们可以使用二重循环,对于每一个查询,枚举所有的点,依次判断它们是否在查询的圆中即可。
如果查询圆的圆心为 (cx,cy)(c_x, c_y)(cx,cy),半径为 crc_rcr,枚举的点坐标为 (px,py)(p_x, p_y)(px,py),那么点在圆中(包括在圆上的情况)当且仅当点到圆心的距离小于等于半径。我们可以用以下方法进行判断:
(cx−px)2+(cy−py)2≤cr2(c_x-p_x)^2 + (c_y-p_y)^2 \leq c_r^2(cx−px)2+(cy−py)2≤cr2
注意这里两侧的距离都进行了平方操作,这样可以避免引入浮点数,产生不必要的误差。
复杂度分析:
- 时间复杂度: O(mn)O(mn)O(mn),其中 mmm 和 nnn 分别是数组 points\textit{points}points 和 queries\textit{queries}queries 的长度。
- 空间复杂度: O(1)O(1)O(1)。
class Solution:def countPoints(self, points: List[List[int]], queries: List[List[int]]) -> List[int]:res = []for i in queries:count = 0for j in points:if pow((i[0] - j[0]) ** 2 + (i[1] - j[1]) ** 2, 1/2) <= i[2]:count += 1res.append(count)return res
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/queries-on-number-of-points-inside-a-circle
相关文章:

算法刷题打卡第91天:统计一个圆中点的数目
统计一个圆中点的数目 难度:中等 给你一个数组 points ,其中 points[i] [xi, yi] ,表示第 i 个点在二维平面上的坐标。多个点可能会有 相同 的坐标。 同时给你一个数组 queries ,其中 queries[j] [xj, yj, rj] ,表…...
sentinel持久化方案
一.sentinel规则推送原理 1.原有内存规则存储原理 (1)dashborad中请求到服务器后,在controller中通过http把规则直接推送给client,client接收后把规则放入内存; 2.持久化推送规则原理 
软件项目进度安排与跟踪:关键路径的计算
在一个软件项目中,管理人员需要按时了解项目进度,制定项目计划,同时需要及时发现所遇到的问题,然后和团队成员制定解决方案,确保整个计划可以顺利的进行,因此项目进度安排与跟踪是项目管理中的一个重要环节…...

mac m2 处理器 iterm2 sz rz 出错/无限重试
mac m2 处理器 iterm2 sz rz 出错/无限重试 1、背景 apple m 系列处理器安装的 homebrew 跟 intel 处理器略有不同,其中安装目录的区别: m 系列处理器安装目录为 /usr/local/bin/homebrewintel 处理器安装目录为 /opt/homebrew 其中 m 系列处理器安装…...
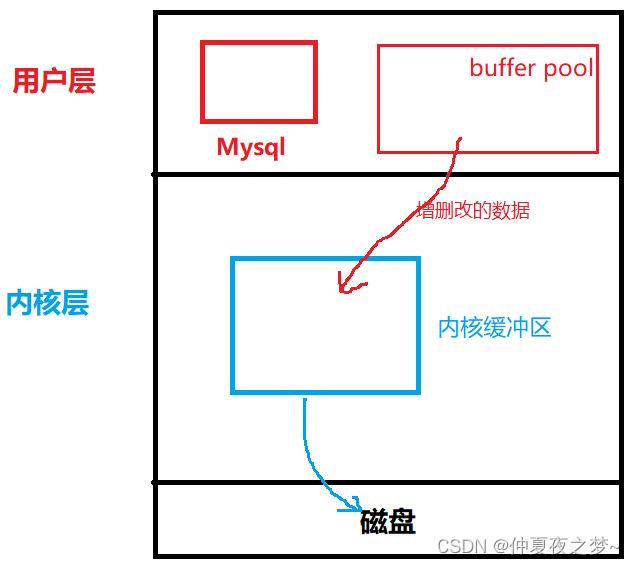
Mysql 与 磁盘交互的过程
从之前的Mysql架构可以了解到,Mysql 客户端不是直接和磁盘打交道,我们在客户端输入的sql语句会被发送给服务端,服务端对sql语句进行解析、缓存等操作,然后再交由存储引擎去读写磁盘。这其实是从 C/S 的角度去了解Mysql。 站在OS的…...
Spring Cloud Gateway集成Nacos实现负载均衡
💡Nacas可以用于实现Spring Cloud Gateway中网关动态路由功能,也可以基于Nacos来实现对后端服务的负载均衡,前者利用Nacos配置中心功能,后者利用Nacos服务注册功能。接下来我们来看下Gateway集成Nacos实现负载均衡的架构图一. 环境…...

Excel图表教程_编程入门自学教程_菜鸟教程-免费教程分享
教程简介 Excel图表初学者教程 - 从简单和简单的步骤学习Excel图表从基本概念到高级概念,包括简介,创建图表,类型,柱形图,折线图,饼图,圆环图,条形图,面积图,…...
2023最新的接口自动化测试面试题
1、请结合你熟悉的项目,介绍一下你是怎么做测试的? -首先要自己熟悉项目,熟悉项目的需求、项目组织架构、项目研发接口等 -功能 接口 自动化 性能 是怎么处理的? -第一步: 进行需求分析,需求评审&#…...
AcWing语法基础课笔记 第一章 C++入门及简单的顺序结构
第一章 C入门及简单的顺序结构 编程是一种控制计算机的方式,和我们平时双击打开文件、关机、重启没有任何区别。 ———闫学灿 C中常用的变量类型 和所占字节大小 输出变量地址符: 软件环境 作业的评测与提交 在线练习地址:www.acwing.com …...

【并发编程】【2】进程与线程
并发编程 2.进程与线程 2.1 进程与线程 进程 程序由指令和数据组成,但这些指令要运行,数据要读写,就必须将指令加载至 CPU,数据加载至内存。在 指令运行过程中还需要用到磁盘、网络等设备。进程就是用来加载指令、管理内存、管…...

MySQL获取当前时间的各种方式
1 获取当前完整时间1.1 now()函数select now();输出:2023-02-15 10:46:171.2 sysdate()函数select sysdate();输出:2023-02-15 10:47:131.3 current_timestamp或current_timestamp()current_timestamp和current_timestamp()函数的效果是一样的,只不过一个是关键字&a…...
及其总结)
redis持久化之AOF(Append Only File)及其总结
1.是什么? 以日志的形式来记录每个写操作,将redis执行过的所有写指令记录下来(读操作不记录),只许追加文件但不可以改写文件,redis启动之初会读取该文件重新构建数据,换言之,redis重启的话就根据日志文件的…...

LeetCode 刷题之队列
5. 队列 队列(queue)是只允许在一端进行插入操作,而在另一端进行删除操作的线性表。 队列是一种先进先出的(First In First Out)的线性表,简称 FIFO。允许插入的一端为队尾,允许删除的一端为队…...
)
互联网摸鱼日报(2023-02-15)
互联网摸鱼日报(2023-02-15) InfoQ 热门话题 ChatGPT火爆全球后,OpenAI CEO称“它很酷,但却是个糟糕的产品” 微软发言人证实旗下LinkedIn平台开始裁员 Akamai 推出 Akamai Connected Cloud 和全新云计算服务 AI赋能元宇宙游戏…...
)
聊聊外包和远程项目的敏捷管理(合辑共7篇)
这是鼎叔的第五十一篇原创文章。行业大牛和刚毕业的小白,都可以进来聊聊。欢迎关注本专栏和微信公众号《敏捷测试转型》,大量原创思考文章陆续推出。第四个合辑完工了,咱们介绍了外包管理或远程项目如何敏捷交付,满足管理层预期。…...

2023-2-15 刷题情况
检查「好数组」 题目描述 给你一个正整数数组 nums,你需要从中任选一些子集,然后将子集中每一个数乘以一个 任意整数,并求出他们的和。 假如该和结果为 1,那么原数组就是一个「好数组」,则返回 True;否则…...
汉诺塔递归算法精讲
文章目录前言一、汉诺塔是个啥?二、手动解法三、解法抽象四、递归解法五、总结前言 递归算法是计算机算法中的基础算法,也是非常重要的算法,从某种程度上讲,它有一点儿AI的影子。人脑是可以完成递归思路的,但是对不起…...

vue的$nextTick的原理
参考:https://cloud.tencent.com/developer/article/1633546 总结一下:就是$nextTick将回调函数放到微任务或者宏任务当中以延迟它地执行顺序;(总结的也比较懒👶) 重要的是理解源码中它的三个参数的意思&a…...

前端学习第一阶段——第五章CSS(下)
5-9 浮动 08-浮动导读 09-传统网页布局三种方式 10-为什么需要浮动 11-什么是浮动 12-浮动特性-脱标 13-浮动特性-浮动元素一行显示 14-浮动特性-浮动元素具有行内块特性 15-浮动元素经常搭配标准流的父元素 16-浮动布局练习1 <!DOCTYPE html> <html lang"en&quo…...
基于django搭建简单的个人博客
文章目录第一步、在Ubuntu中安装虚拟环境并进入第二步、安装blog所需要的包,在requirements.txt中安装mysqlclient可能会报错,输入下列命令后在安装即可成功第三步、创建好数据库,把测试数据导入第四步、修改DjangoBlog包中 settings中数据库…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
