华为OD机试 - 最小施肥机能效(Python)| 真题+思路+考点+代码+岗位
相关文章:
| 真题+思路+考点+代码+岗位)
华为OD机试 - 最小施肥机能效(Python)| 真题+思路+考点+代码+岗位
最小施肥机能效 题目 某农场主管理了一大片果园,fields[i]表示不同果林的面积,单位:( m 2 m^2 m2),现在要为所有的果林施肥且必须在 n 天之内完成,否则影响收成。 小布是果林的工作人员,他每次选择一片果林进行施肥,且一片果林施肥完...

vue2 使用 cesium 篇
vue2 使用 cesium 篇 今天好好写一篇哈,之前写的半死不活的。首先说明:这篇博文是我边做边写的,小白也是,实现效果会同时发布截图,如果没有实现也会说明,仅仅作为技术积累,选择性分享࿰…...

2023预测:PKI将受到企业重点关注
2023年,PKI作为关键业务将继续被主流企业关注,根据Keyfactor发布的报告显示,很多企业正努力实施PKI,而以下因素是影响企业决策的主要原因:1、66% 的企业正在其IT环境中部署更多的密钥和证书,而70%的企业表示…...

linux基本功系列之grep命令
文章目录前言一. grep命令介绍二. 语法格式及常用选项三. 参考案例3.1 搜索文件中以root开头的文件3.2 搜索文件中出现的root3.3 搜索除了匹配行之外的行3.4 匹配的部分使用颜色显示3.5 只输出文件中匹配到的地方3.6 输出包含匹配字符串的行,并显示所在的行数3.7 统…...

硬件设计——DDR
一、DDR简介 (1)DDRDouble Data Rate双倍速率同步动态随机存储器。严格的说DDR应该叫DDR SDRAM,人们习惯称为DDR,其中,SDRAM 是Synchronous Dynamic Random Access Memory的缩写,即同步动态随机存取存储器。…...

最近你提前还贷了吗
最近你有想过提前还贷吗?以前,欠别人的是大爷,借别人钱的是孙子。现在好像反过来了呀,想还钱成了孙子。现在,各种银行以各种方式增加你提前还贷的难度。比如第一步,关闭app线上还款入口第二步,需…...

关于STM32常用的8种GPIO输入输出模式的理解
目录 GPIO共有8中输入输出模式,分别是:上拉输入、下拉输入、浮空输入、模拟输入、开漏输出、推挽输出、开漏复用输出、推挽复用输出 ,下面我们详细介绍以下上面的八种输入输出模式。 一、输入模式 (1)上拉输入&#x…...
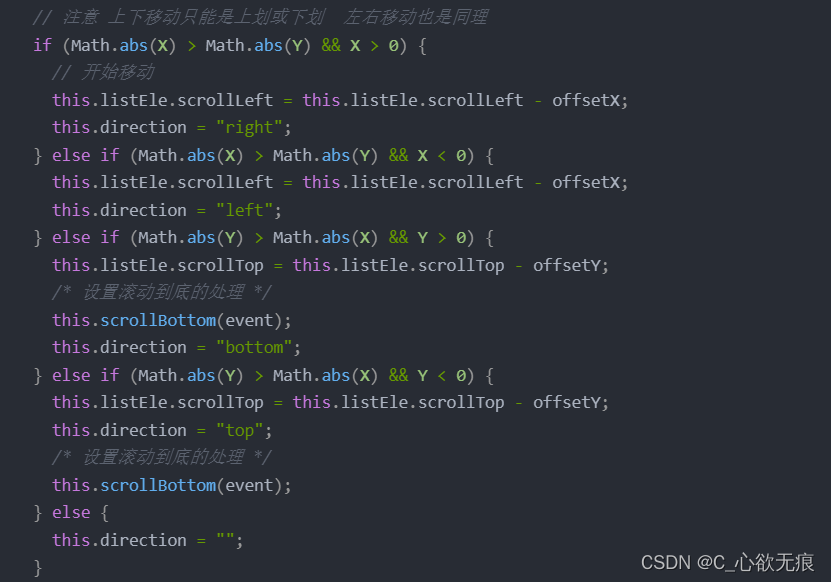
vue - vue项目中解决 IOS + H5 滑动边界橡皮筋弹性效果
问题: 最近遇到一个问题,我们在企业微信中的 H5 项目中需要用到table表格(支持懒加载 上划加载数据)。但是他们在锁头、锁列的情况下,依旧会出现边界橡皮筋效果。就会显示的很奇怪。 什么是ios橡皮筋效果: 我们知道元素…...
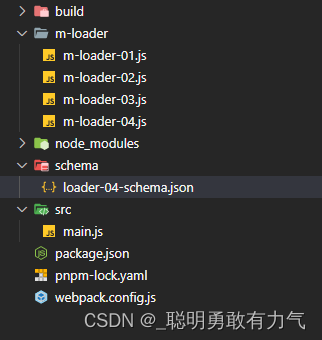
webpack(高级)--创建自己的loader 同步loader 异步loader loader参数校验
webpack 创建自己的loader loader是用于对模块的源代码进行转换(处理) 我们使用过很多loader 比如css-loader style-loader babel-loader 我么如果想要自己创建一个loader 首先创建webpack环境 pnpm add webpack webpack-cli -D 之后创建loader模块…...

Assignment写作各个部分怎么衔接完美?
Assignment格式很简单,就只有四个部分,按着通用的套路来,发现也没什么难度。不过这4个部分自己需要衔接完美,下面就给大家分享一下写Assignment最简单的方法。 如果没有目录可以放在第一页的开头,用“标题字体”加重显…...

医疗器械实验室设计规划全了SICOLAB
一、通用型实验室医疗器械物理性能能检测中,有部分通用型试验,可覆盖不同产品检测,这些实验室需要重点考虑、设计。1、微粒检测室微粒检测室用于医疗器械产品微粒检测,包括微粒、落絮、药液滤除率等项目。微粒检测室要求为洁净室&…...
2023年浙江建筑施工物料提升(建筑特种作业)模拟试题及答案
百分百题库提供特种工(物料提升机)考试试题、特种工(物料提升机)考试预测题、特种工(物料提升机)考试真题、特种工(物料提升机)证考试题库等,提供在线做题刷题,在线模拟考…...

shell编程经典案例,建议收藏
1、编写hello world脚本 #!/bin/bash# 编写hello world脚本echo "Hello World!"2、通过位置变量创建 Linux 系统账户及密码 #!/bin/bash# 通过位置变量创建 Linux 系统账户及密码#$1 是执行脚本的第一个参数,$2 是执行脚本的第二个参数 useradd "$1" …...

C++通用容器
容器简介1.1 容器的分类序列容器 vector, list, deque容器适配器 queue, stack, priority_queue关联容器 set, map, multiset, multimap序列容器是提供一组线性储存的容器,而容器适配器负责将它们按照数据结构的方式组织起来,关联容器提供关键字与值之间…...
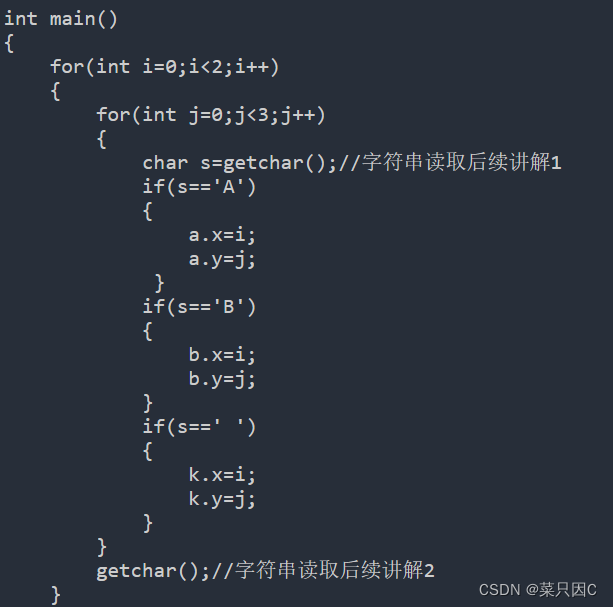
字符串的特殊读取——基于蓝桥杯两道题目(C/C++)
目录 1 例题 1.1 卡片换位 1.2 人物相关性分析 2 字符串的读取 2.1 综述 2.2 scanf 2.3 getline/getchar/get 2.4 注意 2.5 说明 先看例题 1 例题 1.1 卡片换位 问题描述 你玩过华容道的游戏吗? 这是个类似的,但更简单的游戏。 看…...
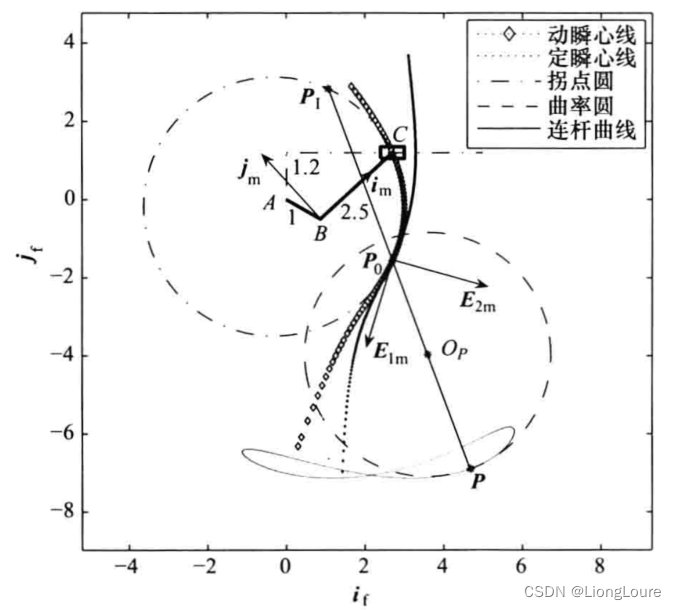
[足式机器人]Part3机构运动微分几何学分析与综合Ch01-4 平面运动微分几何学——【读书笔记】
本文仅供学习使用 本文参考: 《机构运动微分几何学分析与综合》-王德伦、汪伟 《微分几何》吴大任 Ch01-4 平面运动微分几何学1.2.3-2 点轨迹的Euler-Savary公式1.2.4 高阶曲率理论1.2.3-2 点轨迹的Euler-Savary公式 例1-7: 平面曲柄摇杆机构的 Euler-Sa…...

【每日一题Day120】LC2341数组能形成多少数对 | 哈希表 排序
数组能形成多少数对【LC2341】 给你一个下标从 0 开始的整数数组 nums 。在一步操作中,你可以执行以下步骤: 从 nums 选出 两个 相等的 整数从 nums 中 移除这两个整数,形成一个 数对 请你在 nums 上多次执行此操作直到无法继续执行。 返回一…...
win11/10+opencv3.x/4.x配置 VS2019方法(简单使用,亲测)
首先下载 opencv,去官网下载百度》输入opencv,点击opencv|home,进入官网。点击 “Library”---->Release点击 对应版本下的 window版本,点击 --安装--extract---》设置路径。这个就是把库文件扩展到指定的路径下,扩…...

HTTP协议---详细讲解
目录 一、HTTP协议 1.http 2.url url的组成: url的保留字符: 3.http协议格式编辑 ①http request ②http response 4.对request做出响应 5.GET与POST方法 ①GET ②POST 7.HTTP常见Header ①Content-Type:: 数据类型(text/html等)在上文…...

Syntax-Aware Aspect-Level Sentiment Classification with PWCN 论文阅读笔记
一、作者 Chen Zhang, Qiuchi Li, and Dawei Song. 2019. Syntax-Aware Aspect-Level Sentiment Classification with Proximity-Weighted Convolution Network. In Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information …...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
