「SDOI2009」HH去散步
HH去散步
题目限制
- 内存限制:125.00MB
- 时间限制:1.00s
- 标准输入
- 标准输出
题目知识点
- 动态规划 dpdpdp
- 矩阵
- 矩阵乘法
- 矩阵加速
- 矩阵快速幂
- 思维
- 构造
题目来源
「SDOI2009」HH去散步
题目
题目背景
HH 有个一成不变的习惯,喜欢在饭后散步,就是在一定的时间内,走一定的距离
同时, HH 是一个喜欢变化的人,她不会立刻沿着刚刚走过来的路走回去,她也希望每天走过的路径都不完全一样,她想知道每一天他究竟有多少种散步的方法
题目描述
现在 HH 送给你一张学校的地图,请你帮助她求出从地点 AAA 走到地点 BBB 一共有多少条长度为 TTT 的散步路径(答案对 459894598945989 取模)
格式
输入格式
输入共 M+1M + 1M+1 行:
第 111 行:输入 555 个整数 N,M,T,A,BN, \ M, \ T, \ A, \ BN, M, T, A, B;NNN 表示 学校里的路口的个数(编号为 0∼N−10 \sim N - 10∼N−1),MMM 表示 学校里的道路的条数,TTT 表示 HH 想要散步的距离,AAA 表示 散步的出发点, BBB 表示 散步的终点
接下来 MMM 行:每行 222 个用空格隔开的整数 ui,viu_i, \ v_iui, vi;表示 长度为 111 的第 iii 条路 连接 路口 uiu_iui 和 路口 viv_ivi
输出格式
输出共一行:表示你所求出的答案(对 459894598945989 取模)
样例
样例输入
4 5 3 0 0
0 1
0 2
0 3
2 1
3 2
样例输出
4
提示
数据范围
对于 30%30 \%30% 的数据:满足 N≤4,M≤10,T≤10N \leq 4, \ M \leq 10, \ T \leq 10N≤4, M≤10, T≤10
对于 100%100 \%100% 的数据:满足 N≤50,M≤60,T≤230,ui≠viN \leq 50, \ M \leq 60, \ T \leq 2 ^ {30}, \ u_i \neq v_iN≤50, M≤60, T≤230, ui=vi
思路
这道题如果没有 她不会立刻沿着刚刚走过来的路走回去 的限制,就可以根据点与点的关系先构造出一个 n∗nn * nn∗n 的矩阵 x\mathrm{x}x(x[i][j]\mathrm{x}[i][j]x[i][j] 表示从 iii 走 111 步到 jjj 的方案数),累乘 TTT 次(就是走了 TTT 步),就用矩阵快速幂优化既可以通过了
现在就考虑加上这句话的限制后如何构造矩阵了
分析
考虑矩阵定义大致不变,即 x[i][j]\mathrm{x}[i][j]x[i][j] 表示从 iii 走 111 步到 jjj 的方案数
由于有限制,就要记录刚刚走过来的路是哪一条
不妨把每条边对应的 uiu_iui 和 viv_ivi 拆成两个二元组 (node,id)\mathrm{(node, id)}(node,id),表示刚刚从第 id\mathrm{id}id 条路走到 node\mathrm{node}node,也就是每条无向边 (ui↔,vi)(u_i \leftrightarrow, v_i)(ui↔,vi) 分成两条有向边 (ui→vi)(u_i \to v_i)(ui→vi) 和 (vi→ui)(v_i \to u_i)(vi→ui),其中 node\mathrm{node}node 表示当前这条有向边的终点,id\mathrm{id}id 表示与之对应的无向边的编号
那么 x[i][j]=1\mathrm{x}[i][j] = 1x[i][j]=1 定义就是 第 iii 个二元组 走 111 步到 第 jjj 个二元组 的方案数
其值只可能为 000 或 111(因为只走了 111 步),其中值为 111 的条件就是 idi≠idj\mathrm{id}_i \neq \mathrm{id}_jidi=idj 且 nodei\mathrm{node}_inodei 与 nodej\mathrm{node}_jnodej 有一条边
推出了矩阵,但是还有一个细节,就是第一步的方案数
起始点是没有上一条边的,所以需要预处理一下(这里相当于先走了一次)
预处理矩阵 ×\times× 矩阵快速幂(T−1T - 1T−1 次,预处理走了一次)就可以得到最终的矩阵了
最后把 起始点(超级源点) 到 终点(可能有多个,因为分了边) 的路径加起来取模就可以了
代码
#include <cstdio>
#include <cstring>int rint()
{int x = 0, fx = 1; char c = getchar();while (c < '0' || c > '9') { fx ^= ((c == '-') ? 1 : 0); c = getchar(); }while ('0' <= c && c <= '9') { x = (x << 3) + (x << 1) + (c ^ 48); c = getchar(); }if (!fx) return -x;return x;
}const int MOD = 45989;const int MAX_N = 20;
const int MAX_M = 60;int N, M, T, A, B, node;
int e[MAX_M * 2 + 5][3];struct Matrix
{int mx[MAX_M * 2 + 5][MAX_M * 2 + 5];Matrix () { memset(mx, 0, sizeof(mx)); }void init() { for (int i = 0; i <= node; i++) mx[i][i] = 1; }Matrix operator * (const Matrix &rhs) const{Matrix res;for (int i = 0; i <= node; i++)for (int j = 0; j <= node; j++)for (int k = 0; k <= node; k++)res.mx[i][j] = (res.mx[i][j] + mx[i][k] * rhs.mx[k][j]) % MOD;return res;}
} dp, quick;Matrix qpow(Matrix mx, int k)
{Matrix res; res.init();while (k > 0){if (k & 1) res = res * mx;mx = mx * mx; k >>= 1;}return res;
}int main()
{N = rint(), M = rint(), T = rint();A = rint() + 1, B = rint() + 1;for (int i = 1; i <= M; i++){e[i][0] = rint() + 1, e[i][1] = rint() + 1;e[i + M][0] = e[i][1], e[i + M][1] = e[i][0];if (e[i][0] == A) ++dp.mx[0][i];if (e[i + M][0] == A) ++dp.mx[0][i + M];}node = M << 1;for (int i = 1; i <= node; i++)for (int j = 1; j <= node; j++)if (i + M != j && i - M != j && e[i][1] == e[j][0]) ++quick.mx[i][j];int ans = 0;Matrix res = dp * qpow(quick, T - 1);for (int i = 1; i <= node; i++)if (e[i][1] == B) ans = (ans + res.mx[0][i]) % MOD;printf("%d\n", ans);return 0;
}相关文章:

「SDOI2009」HH去散步
HH去散步 题目限制 内存限制:125.00MB时间限制:1.00s标准输入标准输出 题目知识点 动态规划 dpdpdp矩阵 矩阵乘法矩阵加速矩阵快速幂 思维 构造 题目来源 「SDOI2009」HH去散步 题目 题目背景 HH 有个一成不变的习惯,喜欢在饭后散步…...

用上Visual Studio后,我的世界游戏的构建时间减少了一半
今天我们讲述一个使用 Visual Studio 提升工作效率的案例。 我的世界(Minecraft) 游戏开发商 Mojang Studios 近日联系了 Visual Studio C 团队,因为他们需要将 C 开发扩展到新平台(Linux),同时还希望保留他们现有的技术基础&…...
34、基于51单片机锂电池电压电流容量检测仪表LCD液晶显示 原理图PCB程序设计
方案选择 单片机的选择 方案一:AT89C52是美国ATMEL公司生产的低电压,高性能CMOS型8位单片机,器件采用ATMEL公司的高密度、非易失性存储技术生产,兼容标准MCS-51指令系统,片内置通用8位中央处理器(CPU)和Flash存储单元…...
-基础使用)
【Java基础】泛型(一)-基础使用
本文以Java的官方文档为参考,辅以代码示例,尽可能详尽的叙述泛型的每一个特性 什么是泛型 泛型(Generics)也称为参数化类型(parameterized types),也就是将类型本身作为接口、类、方法中的参数…...

学Python不会不知道NumPy计算包吧,带你五分钟看懂NumPy计算包
从今天我们就开始进入 Python 数据分析工具的教程。 前段时间数据分析和Python都讲了一点点,但是Python的数据库,讲的少了点,所以接下来就讲讲这些重要的常用数据库吧!!! Python 数据分析绝对绕不过的四个…...
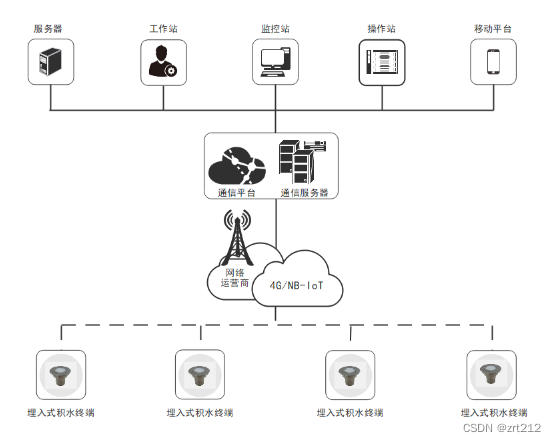
积水内涝监测——埋入式积水终端设备介绍
一、设备概述 埋入式积水终端是针对城市内涝推出的积水信息监测采集设备,采用超声波传感技术,对积水的深度进行精确的测量。产品能够在低温、腐蚀环境下可靠运行本产品特别适用于智慧城市中,对城市道路、社区低洼处的积水进行实时监测上报到…...
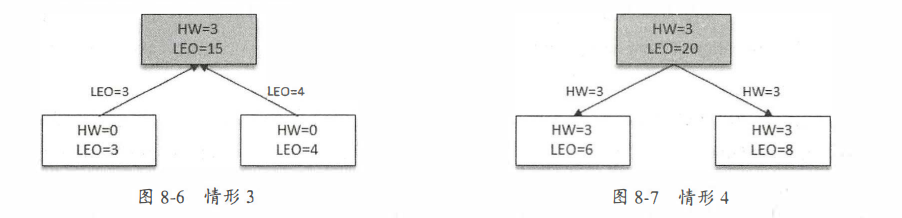
Kafka的日志同步
首先介绍下LEO和HW LEO: 即LogEndOffset,表示该副本下次日志记录的偏移量HW:即HighWatermark,高水位线,是所有ISR副本集合中的LEO最小值上图中,如果此时三个副本都在ISR集合中,那么此时他们的LE…...
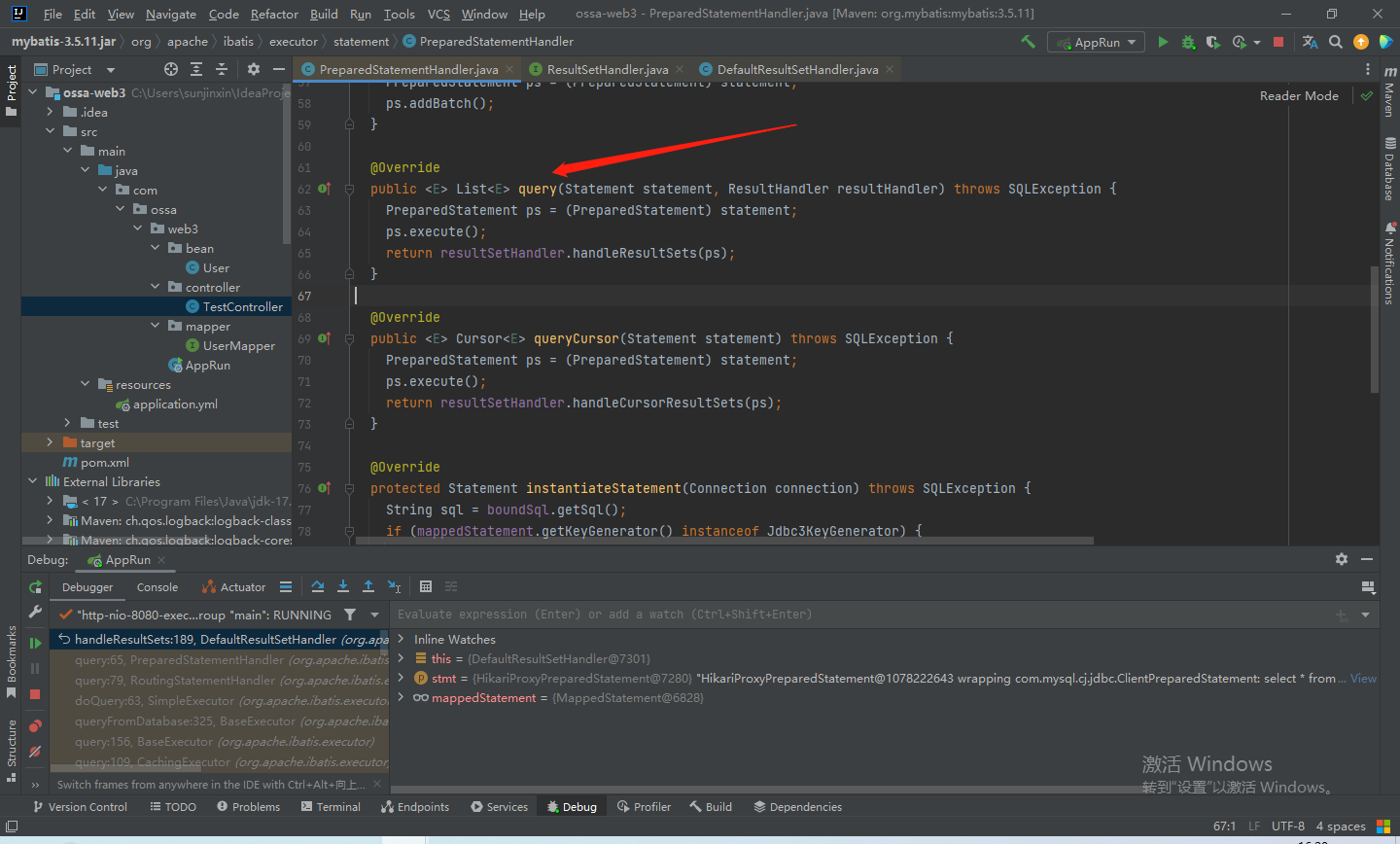
【Mybatis源码解析】mapper实例化及执行流程源码分析
文章目录简介环境搭建源码解析基础环境:JDK17、SpringBoot3.0、mysql5.7 储备知识:《【Spring6源码・AOP】AOP源码解析》、《JDBC详细全解》 简介 基于SpringBoot的Mybatis源码解析: 1.如何对mapper实例化bean 在加载BeanDefinition时&a…...
分布式文件管理系统(MinIO)
1.去中心化,每个点是对等的关系,通过Ngix对负载做均衡工作。 好处: 能够避免单点故障,将多块硬盘组成一个对象存储服务。 2. 使用纠删编码技术来保护数据,是一种回复丢失和损坏的数据的数学算法,他将数据分…...

Springcloud-配置中心config
一、添加依赖<dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-config-server</artifactId></dependency><dependency><groupId>org.springframework.boot</groupId><artifactId&…...

[项目篇] 音乐播放器开发报告
文章目录1. 项目描述:2. 项目上线展现:3. 项目具体实现:1. 登录2. 注册3.退出系统4.添加音乐4.1前后端交互约定4.2上传文件业务逻辑:4.3创建model包中的music类4.4在MusicMapper接口中,声明insertMusic抽象方法4.5在mybatis包中添…...
Spring Cloud Alibaba--gateway微服务详解之网关(二)
1、网关介绍 上篇对微服务中的nacos注册中心进行集成讲解。nacos主要作用是管理多服务之间复杂关系的组件。微服务是非常庞大且问题突出的架构,HTTP协议具有跨源资源共享 (CORS) Cross- Origin Resource Sharing机制,而处于安全考虑往往前端架构都会对跨…...
Zynq非VDMA方案实现视频3帧缓存输出,无需SDK配置,提供工程源码和技术支持
目录1、前言2、VDMA的不便之处3、FDMA取代VDMA实现视频缓存输出4、Vivado工程详解5、上板调试验证并演示6、福利:工程代码的获取1、前言 对于Zynq和Microblaze的用户而言,要想实现图像缓存输出,多半要使用Xilinx推荐的VDMA方案,该…...

血液透析过滤芯气密性检测装置中的高精度多段压力控制解决方案
摘要:针对目前血液过滤芯气密性检测过程中存在的自动化水平较低、多个检测压力之间需人工切换和压力控制精度较差的问题,为满足客户对高精度和自动化气密性检测的要求,本文提出了相应的解决方案。解决方案的主要特点是全过程的可编程压力控制…...
PDF加密如何批量解除?快来了解下这个方法
在现代办公环境中,PDF文档的使用非常普遍。然而,由于一些安全需求,有时候PDF文档会被加密,使得只有授权人员可以查看或修改它。但是,如果您需要对许多加密PDF文档进行操作,逐个解密这些文档可能非常费时费力…...

C++——哈希4|布隆过滤器
目录 布隆过滤器 完整代码 布隆过滤器应用 布隆过滤器的查找 布隆过滤器删除 布隆过滤器优点 布隆过滤器缺陷 布隆过滤器海量数据处理 布隆过滤器 位图只能映射整形,而对于字符串却无能为力。 把字符串用哈希算法转成整形,映射一个位置进行标…...
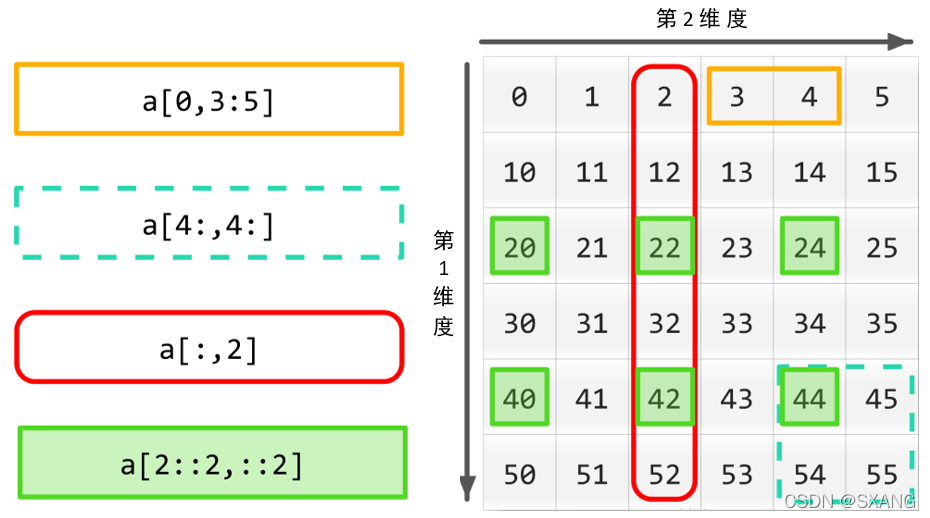
python冒号的用法总结
一维数组 1. 单个冒号的情况 1.1 写完整的情况下 单个冒号的情况下,对数组的遍历操作是从前向后操作。如:arr[a:b] ,冒号前的a含义是从a开始遍历,冒号后的b含义是到b截止(不包括b)。 arr [1, 2, 3, 4,…...

面试题整理
面试题整理 一、Java基础 1、Java 语言有哪些特点 简单易学; 面向对象(封装,继承,多态); 平台无关性( Java 虚拟机实现平台无关性); 支持多线程( C 语言…...
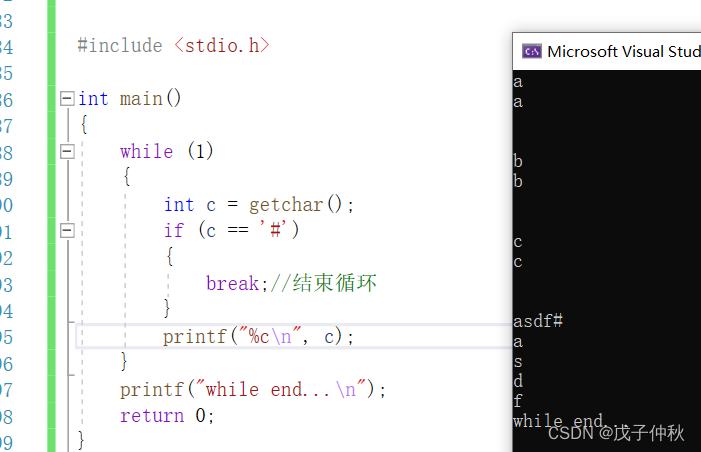
C语言深度解剖-关键字(7)
目录 switch case 语句 理解: 补充: 深入理解: default 语句: case语句: 总结: do、while、for 关键字 while for do while 各种死循环方法: while for do while getchar 写在…...

利用JavaScript编写Python内置函数查询工具
最近我开始学习Python编程语言,我发现Python拥有非常丰富的内置函数,可以用来实现各种不同的功能。但是每当我需要查找一个内置函数时,我总是需要联网使用搜索引擎进行查询。这种方式不仅费时费力,而且需要联网,很不方…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...
