K类函数和KL类函数
Class K \mathcal{K} K function- K \mathcal{K} K类函数
Definition: A continuous function α : [ 0 , a ) → [ 0 , ∞ ) \alpha:[0,a)\rightarrow[0,\infin) α:[0,a)→[0,∞) is said belong to class K \mathcal{K} K if it strictly increasing and α ( 0 ) = 0 \alpha(0)=0 α(0)=0. It is said to belong to class K ∞ \mathcal{K_{\infin}} K∞ if a = ∞ a=\infin a=∞ and α ( r ) → ∞ \alpha(r)\rightarrow\infin α(r)→∞ as r → ∞ r\rightarrow \infin r→∞.
译:如果连续函数 α : [ 0 , a ) → [ 0 , ∞ ) \alpha:[0,a)\rightarrow[0,\infin) α:[0,a)→[0,∞) 严格递增且满足 α ( 0 ) = 0 \alpha(0)=0 α(0)=0,则 α \alpha α 属于 K \mathcal{K} K 类函数。进一步,如果 a = ∞ a=\infin a=∞ 且当 r → ∞ r\rightarrow \infin r→∞ 时有 α ( r ) → ∞ \alpha(r)\rightarrow\infin α(r)→∞ 成立,则 α \alpha α 属于 K ∞ \mathcal{K_\infin} K∞ 类函数。
Class K L \mathcal{KL} KL function- K L \mathcal{KL} KL类函数
Definition: A continuous function β : [ 0 , a ) × [ 0 , ∞ ) → [ 0 , ∞ ) \beta:[0,a)\times[0,\infin)\rightarrow[0,\infin) β:[0,a)×[0,∞)→[0,∞) is said belong to class K L \mathcal{KL} KL if, for each fixed s s s, the mapping β ( r , s ) \beta(r,s) β(r,s) belongs to class K \mathcal{K} K with respected to r r r and, for each fixed r r r, the mapping β ( r , s ) \beta(r,s) β(r,s) is decreasing with respected to s s s and β ( r , s ) → 0 \beta(r,s)\rightarrow 0 β(r,s)→0 as s → ∞ s\rightarrow \infin s→∞.
译:对于连续函数 β : [ 0 , a ) × [ 0 , ∞ ) → [ 0 , ∞ ) \beta:[0,a)\times[0,\infin)\rightarrow[0,\infin) β:[0,a)×[0,∞)→[0,∞),如果对于每个固定的 s s s,映射 β ( r , s ) \beta(r,s) β(r,s) 都是关于 r r r 的 K \mathcal{K} K 类函数, 而对于每个固定的 r r r,映射 β ( r , s ) \beta(r,s) β(r,s) 是关于 s s s 的递减函数,且当 s → ∞ s\rightarrow \infin s→∞ 时 β ( r , s ) → 0 \beta(r,s)\rightarrow 0 β(r,s)→0,则 β \beta β属于 K L \mathcal{KL} KL 类函数。
参考文献
【1】Hassan K. Khalil, Nonlinear Systems, 3 edition, page 144.
相关文章:

K类函数和KL类函数
Class K \mathcal{K} K function- K \mathcal{K} K类函数 Definition: A continuous function α : [ 0 , a ) → [ 0 , ∞ ) \alpha:[0,a)\rightarrow[0,\infin) α:[0,a)→[0,∞) is said belong to class K \mathcal{K} K if it strictly increasing and α ( 0 ) 0 …...
华为OD机试之完美走位(Java源码)
完美走位 题目描述 在第一人称射击游戏中,玩家通过键盘的A、S、D、W四个按键控制游戏人物分别向左、向后、向右、向前进行移动,从而完成走位。 假设玩家每按动一次键盘,游戏任务会向某个方向移动一步,如果玩家在操作一定次数的键…...
或特别的视频组件具体实现方法)
Vue 原始(传统)或特别的视频组件具体实现方法
一、原始的播放器组件(传统的视频播放组件) 参考链接 1. Vue2视频播放(Video) 二、自定义视频播放组件,自播放,无控制模式 简单点的理解,就是没有点击就会暂停播放视频,还有忽略…...

香豆素荧光标记652966-03-5,ATTO425 acid,ATTO 425 羧酸,进行简析说明
中文名称:ATTO 425 羧酸 英文名称:ATTO425 COOH,ATTO-425 carboxylic acid 规格标准:10mg,25mg,50mg CAS:652966-03-5 分子式:C22H27NO6 分子量:401.46结构式:…...

linux信号量与PV操作知识点总结
信号量 信号量(semaphore) 与已经介绍过的 IPC 结构不同,它是一个计数器,信号量用于实现进程间的与斥与同步,而不是用于存储进程间通信数据。 1、特点 (1)信号量用于进程间同步,若要在进程间传递数据需要结…...

6-python中的string类型
目录 内容提要字符串截取python的转义字符 \python的字符串格式化format()的参数format()的数字格式化 字符串常用函数count()函数endwith()函数 与 startwith()函数find()函数与index()函数find()函数 ⭐index()函数 判断字符串内的字符种类函数isalnum()函数isalpha()函数isd…...
Windows系统内核溢出漏洞提权
目录 Windows内核溢出漏洞原理 溢出漏洞简介 什么是缓冲区 缓冲区溢出 缓冲区溢出目的 Windows内核溢出漏洞利用流程 提权实战思路 手工提权测试 辅助提权 EXP如何寻找 使用MSF提权 关于提权时可能遇到的问题 如果提权的时候发现无法执行命令的话,可以上…...
BlackIce病毒分析
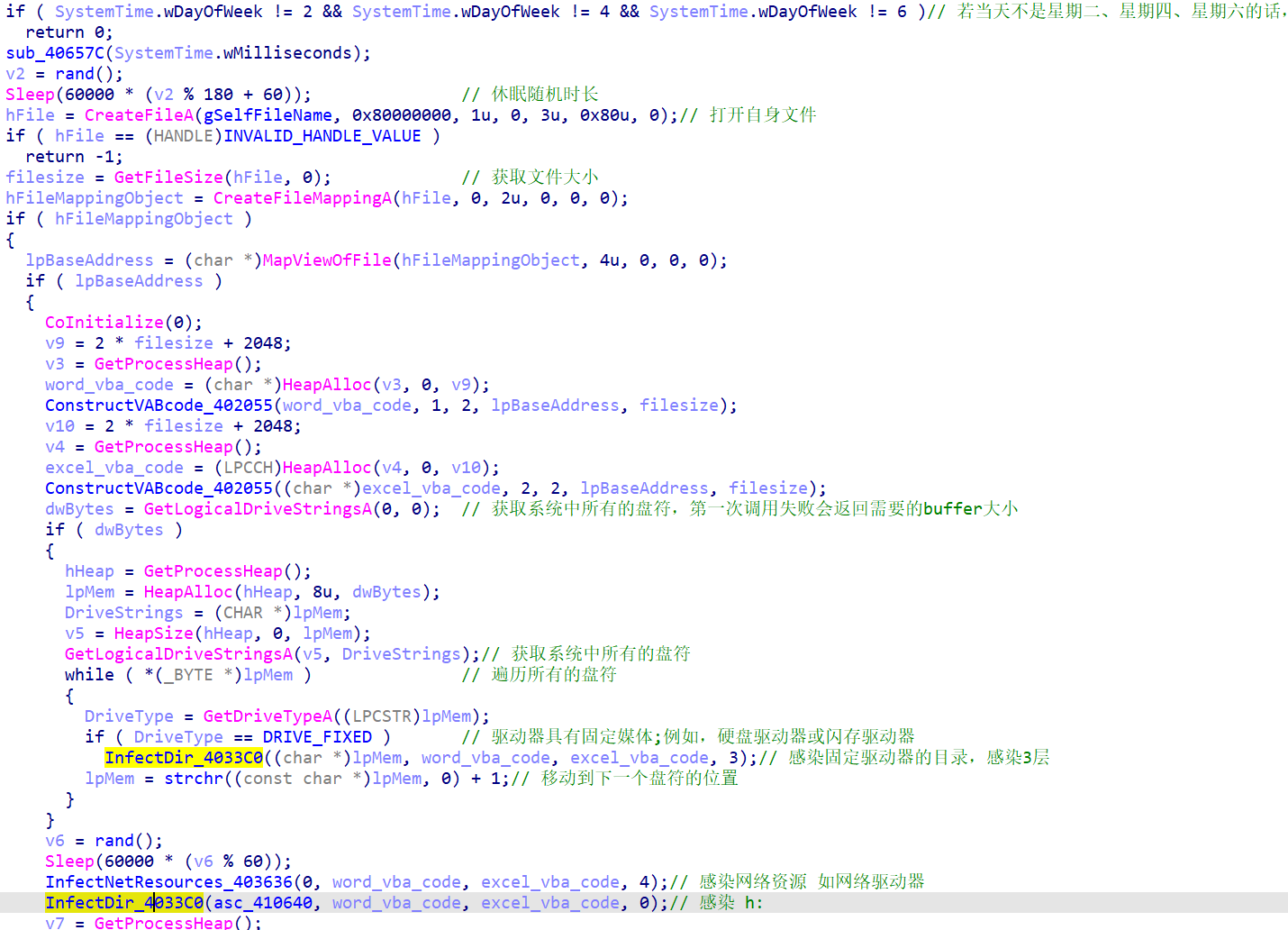
概述 blackice是一个古老的感染型病毒,可感染系统中exe、doc和xls文件,通过USB设备和网络驱动器来传播,会向C&C下载pe执行,会关闭常用的杀软进程。下面找了一个样本,这个样本的代码结构清晰,用IDA pro…...
软件测试基础知识整理(八)- 软件缺陷
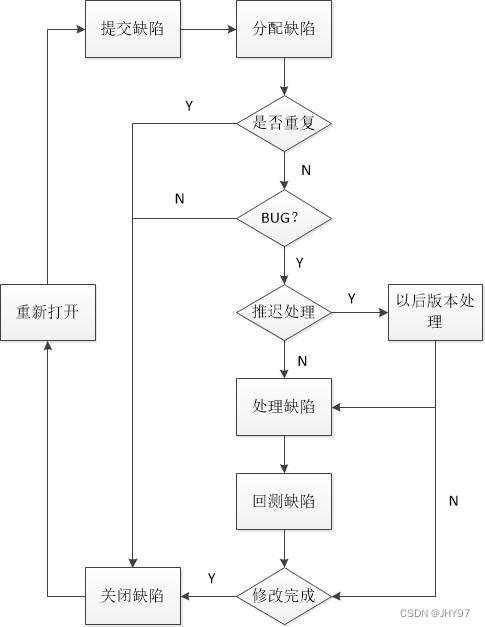
目录 一、软件缺陷 1.1 缺陷定义 1.2 缺陷判定标准 1.3 软件缺陷产生的原因 1.4 软件缺陷产生的根源 1.5 软件缺陷信息 1.5.1 缺陷状态 1.5.2 缺陷严重程度 1.5.3 缺陷优先级 1.6 缺陷报告模板 1.7 缺陷报告注意事项 1.8 缺陷跟踪流程 1.9 缺陷数据分析关注的问题 …...
有没有想过一种可能,30岁之后,转行去做IT售前?
灵魂拷问 IT行业的变化是非常迅速的,各种新技术、新产品、新观念、新的业务模式层出不穷,不仅是我们,客户也在不断地学习进步,因此我们注定要终身学习。 IT售前这个岗位为许多IT职场人提供了一种新的选择: 你不需要成为某一方面…...

基于决策树的Ensemble方法在边缘计算中的应用
随着物联网的普及,边缘计算已成为一种重要的技术手段。在边缘计算中,数据的处理和分析都是在设备端进行的,而不是通过云端进行。这种技术可以大大降低网络带宽和响应时间,从而提高了用户体验。但是,边缘设备通常受到计…...

golang常见导致panic的场景
1、越界 常见有数组越界和字符串越界 2、空指针引用 直接引用空指针结构体的字段会引发panic,但调用成员方法里如果没引用结构体的字段不会引发panic 3、断言失败 4、map操作错误 map未初始化,可读不可写。 map的value如果是结构体指针…...

Python 修改文件权限+只读后几行 can‘t do nonzero end-relative seeks
读后几行使用File Handle : seek 文件处理 # -*- coding: UTF-8 -*-# 打开文件 fo open("runoob.txt", "rw") print "文件名为: ", fo.nameline fo.readline() print "读取的数据为: %s" % (line)# 重新设置文件读取指针到开头 fo.…...

每日学术速递5.25
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.CV 1.Chupa: Carving 3D Clothed Humans from Skinned Shape Priors using 2D Diffusion Probabilistic Models 标题:Chupa:使用 2D 扩散概率模型从蒙皮形状先验雕…...

GAMES202作业1
目录 Shadow MapCalcLightMVP函数useShadowMap函数Bias函数 最终效果 PCF两个采样函数PCF函数最终效果 PCSSfindBlocker函数PCSS函数最终效果 参考 先放上公式: 后面的积分项是我们在作业0中就做好的blinnphong项,我们要求的就是积分项前,等…...

Android 12.0状态栏居中显示时间和修改时间显示样式
1.概述 在12.0的系统rom定制化开发中,在systemui状态栏系统时间默认显示在左边和通知显示在一起,但是客户想修改显示位置,想显示在中间,所以就要修改SystemUI 的Clock.java 文件这个就是管理显示时间的,居中显示的话就得修改布局文件了 效果图如下: 在这里插入图片描述 …...

湍流的数值模拟方法概述
湍流,又称紊流,是一种极其复杂、极不规则、极不稳定的三维流动。湍流场内充满着尺度大小不同的旋涡,大旋涡尺度可以与整个流畅区域相当,而小漩涡尺度往往只有流场尺度千分之一的数量级,最小尺度旋涡的尺度通过其耗散掉…...
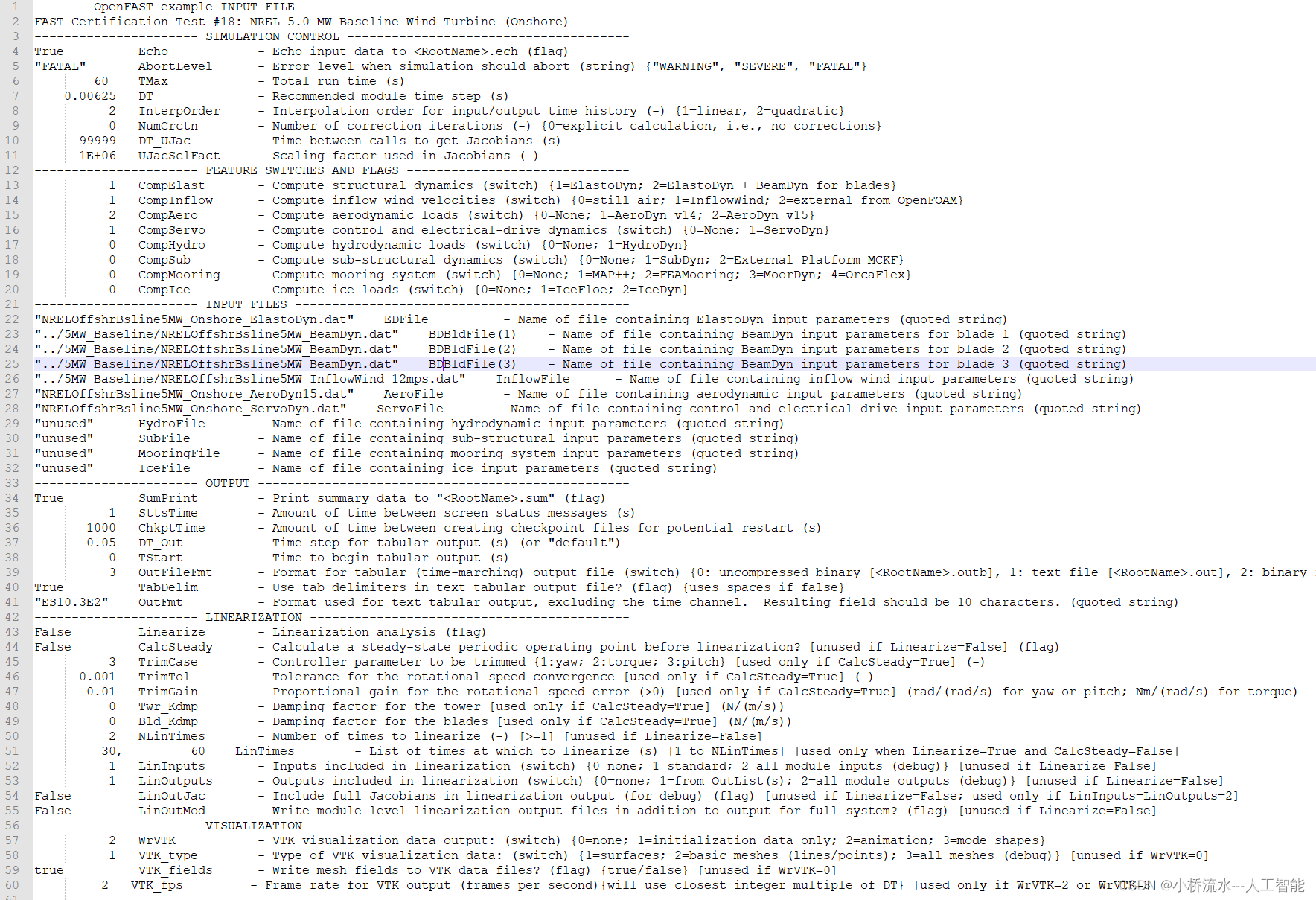
openFast中的陆上风电机组5MW_Land_DLL_WTurb参数详解
文章目录 一、openFAST是什么?二、参数截图三、参数详解 一、openFAST是什么? openFAST是一种开放源代码的工具,为风能工程师提供了用于模拟和设计风力涡轮机的框架。它可以计算风力涡轮机在各种环境条件下的性能,并提供对风力涡…...
“卷”还是“躺平”?职场人如何在工作中找到价值感?
今天不谈技术,只谈进步。 曾经看过一个回答说“职场人最好的姿势是仰卧起坐”。 卷累的就躺,休息好了再继续卷,卷是常态,“仰卧起坐”也好,“卷的姿势”也好,都是在反复“卷起”的过程中寻找一些舒适和平衡…...
《Opencv3编程入门》学习笔记—第二章
《Opencv3编程入门》学习笔记 记录一下在学习《Opencv3编程入门》这本书时遇到的问题或重要的知识点。 第二章 OpenCV 官方例程引导与赏析 openv官方提供的示例程序:具体位于..\opencv\sources\samples\cpp ..\opencv\sources\samples\cpp\tutorial_code路径下存…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
: 发布订阅模式)
JS设计模式(5): 发布订阅模式
解锁JavaScript发布订阅模式:让代码沟通更优雅 在JavaScript的世界里,我们常常会遇到这样的场景:多个模块之间需要相互通信,但是又不想让它们产生过于紧密的耦合。这时候,发布订阅模式就像一位优雅的信使,…...

Python 解释器安装全攻略(适用于 Linux / Windows / macOS)
目录 一、Windows安装Python解释器1.1 下载并安装Python解释1.2 测试安装是否成功1.3 设置pip的国内镜像------永久配置 二、macOS安装Python解释器三、Linux下安装Python解释器3.1 Rocky8.10/Rocky9.5安装Python解释器3.2 Ubuntu2204/Ubuntu2404安装Python解释器3.3 设置pip的…...
