通过强化学习走直线理解基本概念
摘要: 一条线上包含起点和终点共有6个格子,起点在左终点在右。假设智能体已经学到了最优的策略,并且在每一步行动时,以 0.9 0.9 0.9 的概率选择最优策略(也就是往右),以 0.1 0.1 0.1 的概率选择随机策略。各个概念的定义见文末参考链接,本文举实际的数值例子帮助理解。
定义
智能体要从最左边的第一个格子走到最右边的终点一次走一步。把6个格子分别记作状态 s 1 , s 2 , ⋯ , s 6 s_1,s_2,\cdots,s_6 s1,s2,⋯,s6,动作有两种,分别记作 L L L 和 R R R。如果不特别说明,一般随机变量为大写字母,具体数值为小写字母。 L L L 和 R R R 表示动作,不是随机变量。
- 策略函数 (Policy Function) π ( a ∣ s ) \pi(a|s) π(a∣s):在一个状态 s i s_i si 处采取每个动作 a i a_i ai 的概率。简单记作 π ( L ∣ s ) = 0.1 , π ( R ∣ s ) = 0.9 \pi(L|s)=0.1,\pi(R|s)=0.9 π(L∣s)=0.1,π(R∣s)=0.9,严谨写法为
{ π ( A = L ∣ S = s i ) = 0.1 , π ( A = R ∣ S = s i ) = 0.9 , i ≠ 1 π ( A = L ∣ S = s i ) = 0 , π ( A = R ∣ S = s i ) = 1 , i = 1 \begin{cases} \pi(A=L|S=s_i)=0.1,\pi(A=R|S=s_i)=0.9, & i \neq 1 \\ \pi(A=L|S=s_i)=0,\pi(A=R|S=s_i)=1, & i = 1 \\ \end{cases} {π(A=L∣S=si)=0.1,π(A=R∣S=si)=0.9,π(A=L∣S=si)=0,π(A=R∣S=si)=1,i=1i=1
如果在起点处往左走,环境给的反馈是智能体保持在起点不动。
奖励 (Reward): 智能体在状态 s i s_i si 处采取动作 a i a_i ai 后,环境给的奖励 r ( s , a ) r(s,a) r(s,a)。 r ( s = s 5 , a = R ) = 6 r(s=s_5,a=R)=6 r(s=s5,a=R)=6(便于区分),其余的 r ( s , a ) r(s,a) r(s,a) 都是0。
(折扣)回报(Return): 从第 t t t 个回合开始计算的每个回合奖励的总和
U t = r t + γ r t + 1 + γ 2 r t + 2 + ⋯ U t = r t + γ U t + 1 \begin{aligned} & U_t=r_t+\gamma r_{t+1}+\gamma^2r_{t+2}+\cdots \\ & U_t=r_t+\gamma U_{t+1} \end{aligned} Ut=rt+γrt+1+γ2rt+2+⋯Ut=rt+γUt+1
下面都能达到终点的的几个动作和对应的回报分别为 - RRRRR: 0 + 0 γ + 0 γ 2 + 0 γ 3 + 6 γ 4 0+0\gamma+0\gamma^2+0\gamma^3+6\gamma^4 0+0γ+0γ2+0γ3+6γ4
- RRRLRRR: 0 + 0 γ + 0 γ 2 + 0 γ 3 + + 0 γ 4 + 0 γ 5 + 6 γ 6 0+0\gamma+0\gamma^2+0\gamma^3++0\gamma^4+0\gamma^5+6\gamma^6 0+0γ+0γ2+0γ3++0γ4+0γ5+6γ6
- RLRRRRLRR: 0 + 0 γ + 0 γ 2 + 0 γ 3 + + 0 γ 4 + 0 γ 5 + 0 γ 6 + + 0 γ 7 + 6 γ 8 0+0\gamma+0\gamma^2+0\gamma^3++0\gamma^4+0\gamma^5 +0\gamma^6++0\gamma^7+6\gamma^8 0+0γ+0γ2+0γ3++0γ4+0γ5+0γ6++0γ7+6γ8
状态价值函数(State-Value Function): 在状态 s i s_i si 处,采用当前策略 π \pi π 时回报的期望。 V π ( s ) = E ( U t ∣ s = s i ) V_\pi(s)=\mathbb{E}(U_t|s=s_i) Vπ(s)=E(Ut∣s=si)。
动作价值函数(Action-Value Function): 在状态 s i s_i si 处采取动作 a i a_i ai 后,继续保持当前的总体策略 π \pi π 时(也就是以 0.9 0.9 0.9 的概率选择最优策略),回报的期望。 Q π ( s , a ) = E ( U t ∣ s = s i , a = a i ) Q_\pi(s,a)=\mathbb{E}(U_t|s=s_i,a=a_i) Qπ(s,a)=E(Ut∣s=si,a=ai)。
最优动作价值函数(Optimal Action-Value Function): 总是选择最优策略时回报的期望。 Q ∗ ( s , a ) = E ( U t ∣ s = s i , a = a i ) Q^*(s,a)=\mathbb{E}(U_t|s=s_i,a=a_i) Q∗(s,a)=E(Ut∣s=si,a=ai)
下面计算状态价值函数和最优动作价值函数。在这一个例子中,最优动作价值函数就是一直往右走,比较好计算。
Q ∗ ( s = s 1 , a = R ) = 6 γ 4 Q ∗ ( s = s 2 , a = R ) = 6 γ 3 ⋮ Q ∗ ( s = s 5 , a = R ) = 6 \begin{aligned} & Q^*(s=s_1,a=R)=6\gamma^4 \\ & Q^*(s=s_2,a=R)=6\gamma^3 \\ & \vdots \\ & Q^*(s=s_5,a=R)=6 \\ \end{aligned} Q∗(s=s1,a=R)=6γ4Q∗(s=s2,a=R)=6γ3⋮Q∗(s=s5,a=R)=6
下面计算当前策略下每个状态的状态价值函数。这里用到了一个简单的公式
V π ( s ) = E ( U t ∣ s ) = E ( r t ∣ s ) + γ E ( U t + 1 ∣ s ) = r t ( s ) + γ V π ( s t + 1 ) V_\pi(s)=\mathbb{E}(U_t|s) =\mathbb{E}(r_t|s)+\gamma\mathbb{E}(U_{t+1}|s) =r_t(s)+\gamma V_\pi(s_{t+1}) Vπ(s)=E(Ut∣s)=E(rt∣s)+γE(Ut+1∣s)=rt(s)+γVπ(st+1)
其中 E ( r t ∣ s ) = r t ( s ) \mathbb{E}(r_t|s)=r_t(s) E(rt∣s)=rt(s) 表示在状态 s s s 时的期望奖励, s t + 1 s_{t+1} st+1 表示 s s s 的下一个状态。在这个例子中,
E ( r t ∣ s ) = ∑ a P ( a ∣ s ) r ( s , a ) = 0.9 r ( s , R ) + 0.1 r ( s , L ) \mathbb{E}(r_t|s)=\sum_a\mathbb{P}(a|s)r(s,a) =0.9r(s,R)+0.1r(s,L) E(rt∣s)=a∑P(a∣s)r(s,a)=0.9r(s,R)+0.1r(s,L)
于是可以算出每个状态的期望奖励
r ( s 5 ) = 0.9 ⋅ 6 + 0.1 ⋅ 0 r ( s 4 ) = R ( s 3 ) = ( s 2 ) = R ( s 1 ) = 0 \begin{aligned} & r(s_5)=0.9\cdot 6+0.1\cdot 0 \\ & r(s_4)=R(s_3)=(s_2)=R(s_1)=0 \\ \end{aligned} r(s5)=0.9⋅6+0.1⋅0r(s4)=R(s3)=(s2)=R(s1)=0
此时每个状态的状态价值函数为 (已知 V π ( s 6 ) = 6 V_\pi(s_6)=6 Vπ(s6)=6)
V π ( s 5 ) = r ( s 5 ) + γ ( 0.9 ⋅ 6 + 0.1 V π ( s 4 ) ) V π ( s 4 ) = r ( s 4 ) + γ ( 0.9 V π ( s 5 ) + 0.1 V π ( s 3 ) ) V π ( s 3 ) = r ( s 3 ) + γ ( 0.9 V π ( s 4 ) + 0.1 V π ( s 2 ) ) V π ( s 2 ) = r ( s 2 ) + γ ( 0.9 V π ( s 3 ) + 0.1 V π ( s 1 ) ) V π ( s 1 ) = r ( s 1 ) + γ ( 0.9 V π ( s 2 ) + 0.1 V π ( s 1 ) ) \begin{aligned} & V_\pi(s_5)=r(s_5)+\gamma(0.9\cdot 6+0.1V_\pi(s_4)) \\ & V_\pi(s_4)=r(s_4)+\gamma(0.9V_\pi(s_5) + 0.1V_\pi(s_3)) \\ & V_\pi(s_3)=r(s_3)+\gamma(0.9V_\pi(s_4) + 0.1V_\pi(s_2)) \\ & V_\pi(s_2)=r(s_2)+\gamma(0.9V_\pi(s_3) + 0.1V_\pi(s_1)) \\ & V_\pi(s_1)=r(s_1)+\gamma(0.9V_\pi(s_2) + 0.1V_\pi(s_1)) \\ \end{aligned} Vπ(s5)=r(s5)+γ(0.9⋅6+0.1Vπ(s4))Vπ(s4)=r(s4)+γ(0.9Vπ(s5)+0.1Vπ(s3))Vπ(s3)=r(s3)+γ(0.9Vπ(s4)+0.1Vπ(s2))Vπ(s2)=r(s2)+γ(0.9Vπ(s3)+0.1Vπ(s1))Vπ(s1)=r(s1)+γ(0.9Vπ(s2)+0.1Vπ(s1))
设 γ = 0.8 \gamma=0.8 γ=0.8,可以解得
V π ( s 5 ) = 4.602433406284881 V π ( s 4 ) = 3.5304175785610044 V π ( s 3 ) = 2.708319075448633 V π ( s 2 ) = 2.080230236058876 V π ( s 1 ) = 1.6280062716982504 \begin{aligned} & V_\pi(s_5)=4.602433406284881 \\ & V_\pi(s_4)=3.5304175785610044 \\ & V_\pi(s_3)=2.708319075448633 \\ & V_\pi(s_2)=2.080230236058876 \\ & V_\pi(s_1)=1.6280062716982504 \\ \end{aligned} Vπ(s5)=4.602433406284881Vπ(s4)=3.5304175785610044Vπ(s3)=2.708319075448633Vπ(s2)=2.080230236058876Vπ(s1)=1.6280062716982504
求解的python代码如下
import numpy as np
A = np.array([[0.0, 0.08, 0.0, 0.0, 0.0],[0.72, 0.0, 0.08, 0.0, 0.0],[0.0, 0.72, 0.0, 0.08, 0.0],[0.0, 0.0, 0.72, 0.0, 0.08],[0.0, 0.0, 0.0, 0.72, 0.08]])
B = np.eye(5) - A
C = np.array([4.32, 0, 0, 0, 0])
D = np.matmul(np.linalg.inv(B) , C.T)
for n in range(5):print(D[n])
动作价值函数可以采用类似的方法计算。
贝尔曼方程
参考
- 王树森 张志华,《深度强化学习(初稿)》
- Mathematical Foundation of Reinforcement Learning -GitHub
相关文章:

通过强化学习走直线理解基本概念
摘要: 一条线上包含起点和终点共有6个格子,起点在左终点在右。假设智能体已经学到了最优的策略,并且在每一步行动时,以 0.9 0.9 0.9 的概率选择最优策略(也就是往右),以 0.1 0.1 0.1 的概率选…...

Java字符流
5 字符流 5.1 为什么出现字符流 由于字节流操作中文不是特别的方便,所以Java就提供字符流字符流=字节流+编码表用字节流复制文本文件时,文本文件也会有中文,但是没有问题,原因是最终底层操作会自动进行字节拼接成中文,如何识别是中文的呢? 汉字在存储的时候, 无论选择哪…...

2023年上半年信息系统项目管理师上午真题及答案解析
1.“新型基础设施”主要包括信息技术设施、融合基础设施和创新基础设施三个方面。其中信息基础设施包括( )。 ①通信基础设施 ②智能交通基础设施 ③新技术基础设施 ④科教基础设施 ⑤算力基础设施 A.①③⑤ B.①④⑤ C.②③④ D.②…...

LeetCode 739 每日温度
题目: 给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。 示例 1…...
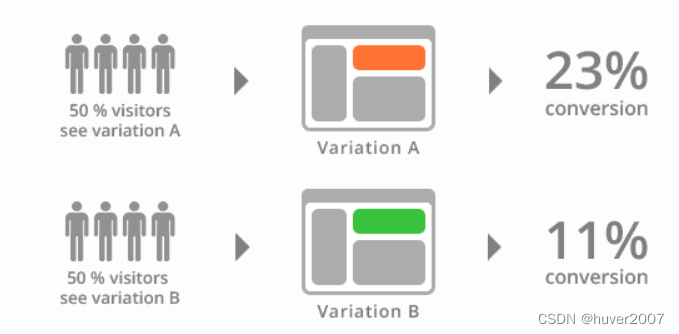
介绍几种常见的运维发布策略
随着Devops的发展,为了提高运维发布的成功率,探索出了多种发布策略。本文简单介绍几种常见发布策略, 以及它们适用的场景和优缺点。 第一种,停机发布 这是最早的一种发布策略,停机发布会在发布以前关闭服务,停止用户…...

C++ QT QDBus进阶用法。
以下是使用QDBus的高级用法示例代码: 1. 使用DBus的异步调用机制: #include <QCoreApplication> #include <QDebug> #include <QDBusConnection> #include <QDBusPendingCallWatcher> class MyDBusObject : public QObject …...
)
2023-5-26 LeetCode每日一题(二进制矩阵中的最短路径)
2023-05-29每日一题 一、题目编号 1091. 二进制矩阵中的最短路径二、题目链接 点击跳转到题目位置 三、题目描述 给你一个 n x n 的二进制矩阵 grid 中,返回矩阵中最短 畅通路径 的长度。如果不存在这样的路径,返回 -1 。 二进制矩阵中的 畅通路径…...

博客系统后端设计(七) - 实现显示用户信息与注销功能
文章目录 1. 显示用户信息1.1 约定前后端交互接口1.2 修改列表页的前段代码1.3 实现详情页的后端代码1.4 实现详情页的前端代码 2. 注销2.1 确定前后端交互接口2.2 实现后端代码2.3 修改前端代码 1. 显示用户信息 此处的用户名是写死的,我们希望的是此处是能够动态生…...
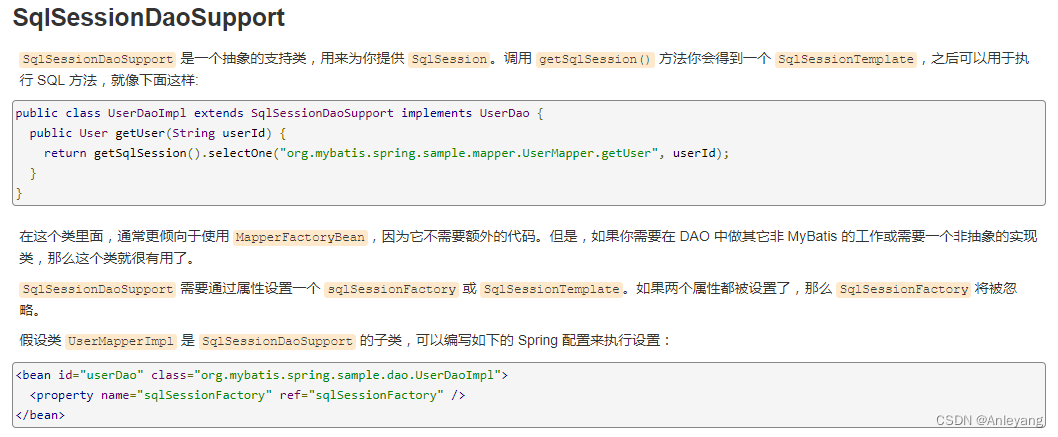
Spring5 学习笔记
前置知识: 掌握Java基础知识(特别是反射)掌握Java注解掌握XML掌握Maven Spring5学习笔记 1、Spring概述1.1、简介1.2、优点1.3、组成1.4、拓展 2、IOC理论推导2.1、分析实现2.2、IOC本质 3、HelloSpring3.1、导入jar包3.2、编写代码3.3、思考…...

leetcode--分隔链表(java)
分割链表 leetcode 86 分割链表 (中等)解题思路:链表专题 leetcode 86 分割链表 (中等) leetcode 86 分割链表 原题链接,可以直接测试 给你一个链表的头节点 head 和一个特定值 x ,请你对链表进…...

使用 AD8232 ECG 传感器和 ESP32 进行基于物联网的 ECG 监测
这篇文章是使用 AD8232 ECG 传感器和 ESP32 进行基于物联网的 ECG 监测。可以从世界任何地方在线观察来自患者心脏的心电图信号。 目录 概述 什么是心电图? 心电图的医疗用途 AD8232 心电图传感器...

【Linux初阶】基础IO - 文件操作(使用系统接口实现) | vim批量注释代码
🌟hello,各位读者大大们你们好呀🌟 🍭🍭系列专栏:【Linux初阶】 ✒️✒️本篇内容:重新理解文件和文件操作,C语言实现的简单文件操作,文本初始权限,系统接口介…...

网络安全之信息收集
第一部分:被动信息收集 1、简介 在信息收集这块区域,我将其分为两部分:第一部分即被动信息收集,第二部分即主动信息收集。 对于标准的渗透测试人员来说,当明确目标做好规划之后首先应当进行的便是信息收…...

ModuleNotFoundError: No module named ‘_lzma‘
安装torchvision报错:ModuleNotFoundError: No module named ‘_lzma’ 参考文章:https://zhuanlan.zhihu.com/p/404162713 解决思路:用backports.lzma代替_lzma包 解决步骤:(ubuntu系统) 安装依赖sudo apt-get install liblzma-d…...

标点符号相关的英语单词
Comma - 逗号 Period - 句号 Question mark - 问号 Exclamation mark - 感叹号 Semicolon - 分号 Colon - 冒号 Quotation marks - 引号 Parentheses - 括号 Brackets - 方括号 Hyphen - 连字符 Dash - 破折号 Ellipsis - 省略号 Apostrophe - 省略符号 Slash - 斜杠 Backslash…...

MyBatis的部分知识点
一、resultMap的constructor配置方式 <resultMap id"" type""> <constructor> <!--主键--> <idArg column"id" javaType"_int"/> <!--其他列--> …...

PAT A1089 Insert or Merge
1089 Insert or Merge 分数 25 作者 CHEN, Yue 单位 浙江大学 According to Wikipedia: Insertion sort iterates, consuming one input element each repetition, and growing a sorted output list. Each iteration, insertion sort removes one element from the input…...
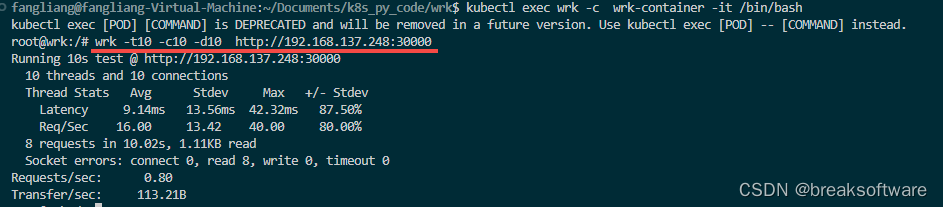
研发工程师玩转Kubernetes——创建一个测试容器
测试容器并不是什么都没有的容器,只是它没有我们期望的常驻进程。我们常用它来做一些测试。 举个例子,在《研发工程师玩转Kubernetes——自动扩缩容》中我们使用本地wrk进行了压力测试。如果我们希望进入容器手工调用wrk,该怎么做呢ÿ…...
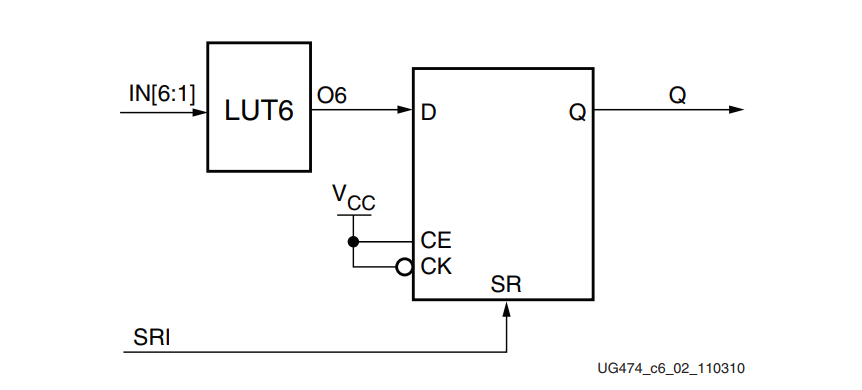
FPGA - 7系列 FPGA内部结构之CLB -03- CLB相关原语以及应用
前言 本文节选UG474的第二章,进行整理翻译。CLB资源被FPGA综合工具自动有效地使用,不需要任何特殊的FPGA专用编码。一些HDL编码建议和技术可以帮助优化设计以获得最大效率。 设计检查清单 这些指南是为有效使用7系列CLB的设计建议提供的快速核对表。7…...

什么是日志关联
什么是日志关联 日志关联是一种分析来自不同源的日志数据以识别事件模式的技术。它用于更好地了解网络的活动,从而有效地保护网络免受漏洞和威胁。 日志关联是日志管理过程的关键部分。收集和存储日志后,集中式日志服务器将执行分析以检测特定事件。日…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...
