数据结构图的基础概念

1、图的概念

图(Graph)：是由顶点的有穷非空集合和顶点之间边的集合组成。
顶点(Vertex)：图中的数据元素。
边(Edge)：顶点之间的逻辑关系,边可以是有向的或无向的，也可以带有权重（可以表示距离，花费等）
无向边：若顶点之间的边没有方向，则称这条边为无向边
有向边：若从顶点 vi 到 νj的边有方向，则称这条边为有向边（一条无向边可以用两条有向边来表示）

无向图

图中任意两个顶点之间的边都是无向边，无向边表示从节点1可以到节点2，也可以从节点2到节点1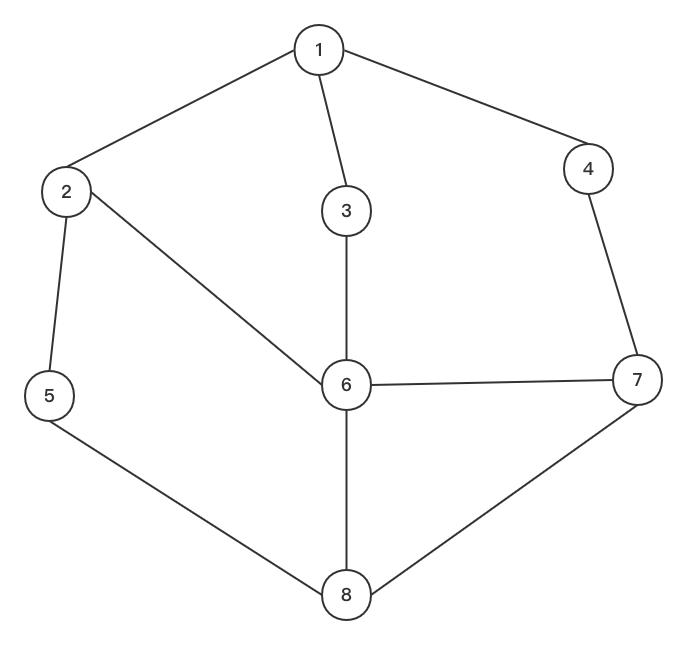

有向图

图中任意两个顶点之间的边都是有向边  图中的方向都是朝向一个方向的，并不是有向图都是朝向一个方向，只是为了方便，有向图可以理解为路径是有方向的，只能按着箭头的方向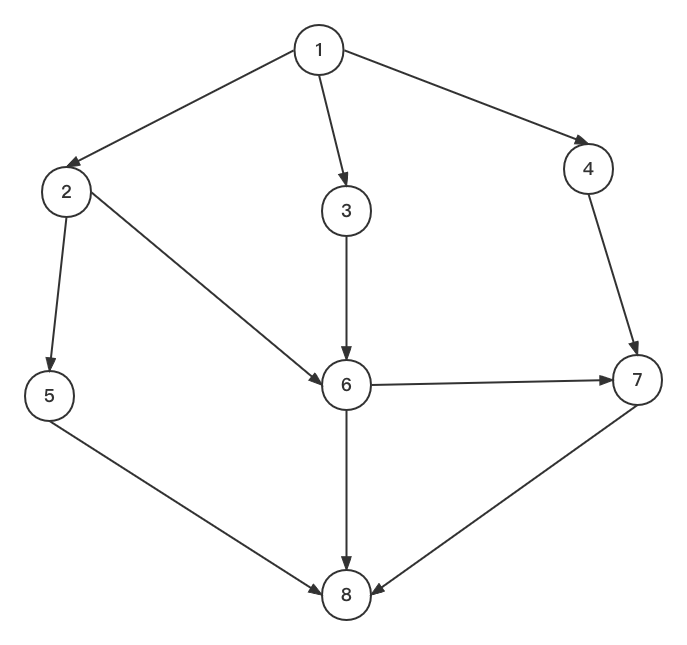

2、图的存储

图的存储常用的邻接矩阵和邻接表
邻接矩阵存储查询简单方便，缺点当遇到的图是稀疏图时会浪费大量空间
邻接表相对邻接矩阵复杂点，优点节省空间，但当图时稠密图时它的优点就不明显了

邻接矩阵

数组（i，j）表示从i到j是否连通，0表示不联通，不为0表示联通

无向图存储

将一条有向边转化为两条有向边，比如 顶点1和顶点2这条无向边转化为顶点1到顶点2和顶点2到顶点1两条有向边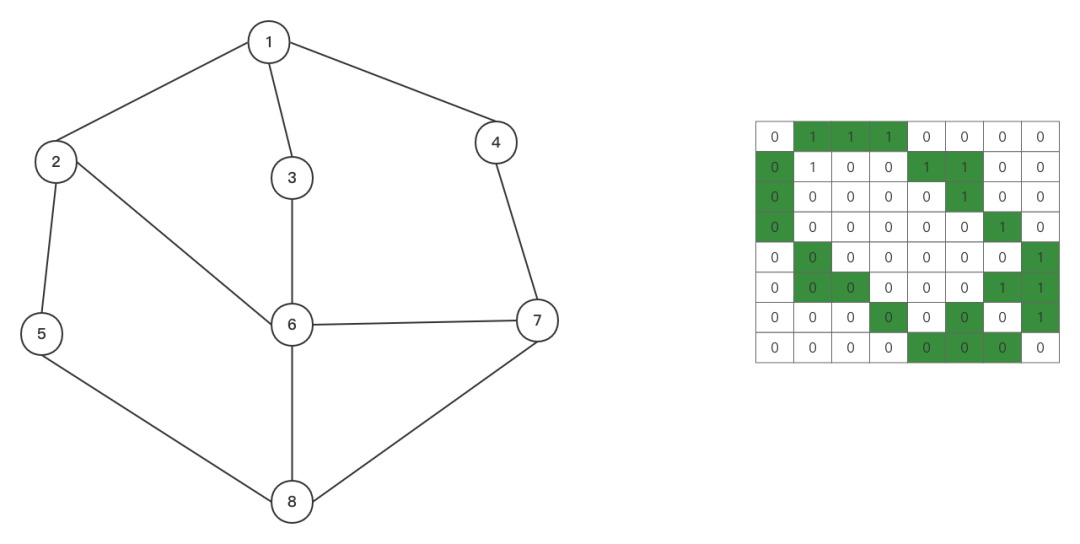

有向图存储

有向图二维数组.png

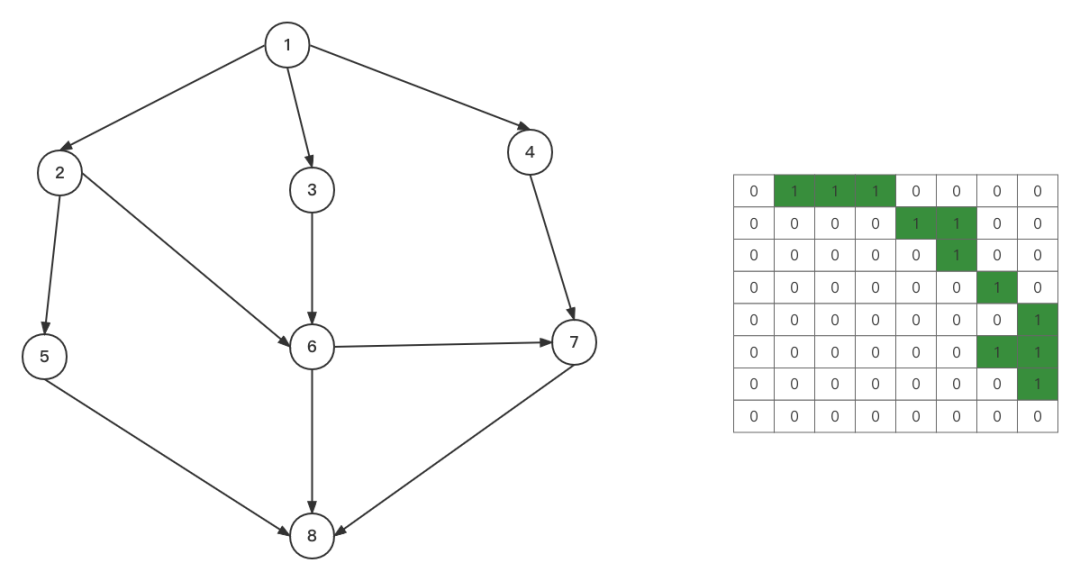
邻接表

有向图邻接表.png

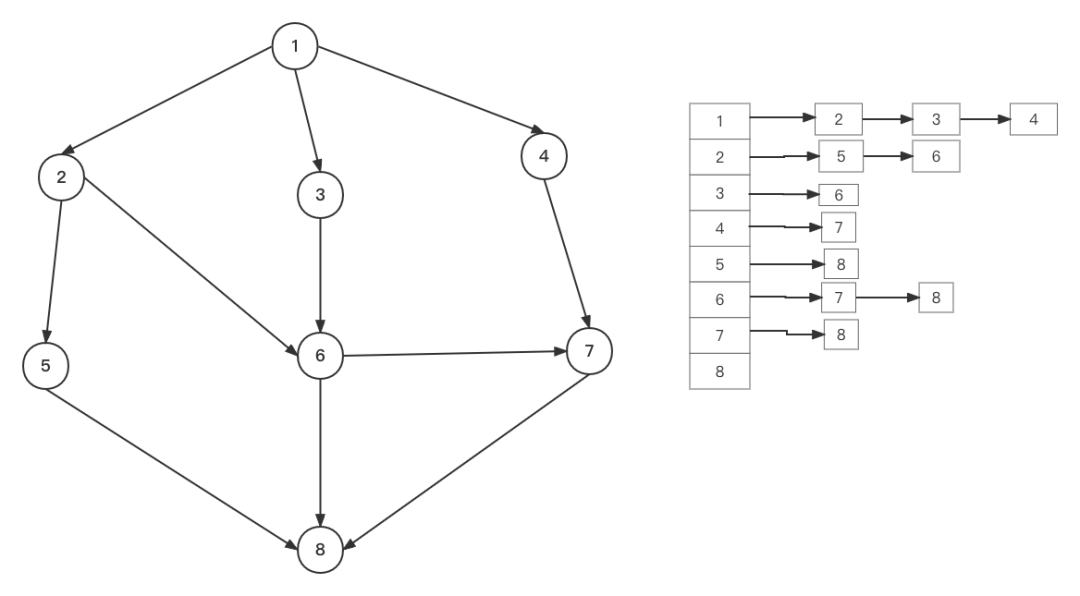
//顶点 class POS{public POS(int head) {this.head = head;}public  int head;//这个值指向的是边}
//边class Edge{public int v;public  int next;}//图的初始化
top =0;//用来记录边的位置
posList =new ArrayList<>();//顶点
edgeList =new ArrayList<>();//边的列表
for(int i = 0;i<=posSize;i++){posList.add(new POS(-1));//初始化hadVisted[i] =false;//初始化}
//添加边邻接表，添加一条从u到v的边public void Add_Edge(int u, int v) {//  1 -> 4->3->2Edge edge =new Edge();edge.v =v;edge.next =posList.get(u).head;posList.get(u).head =top;edgeList.add(edge);top++;}

3、图的搜索

深搜

深搜就是一个递归 1、从顶点1开始遍历，遍历到顶点2，然后从顶点2开始遍历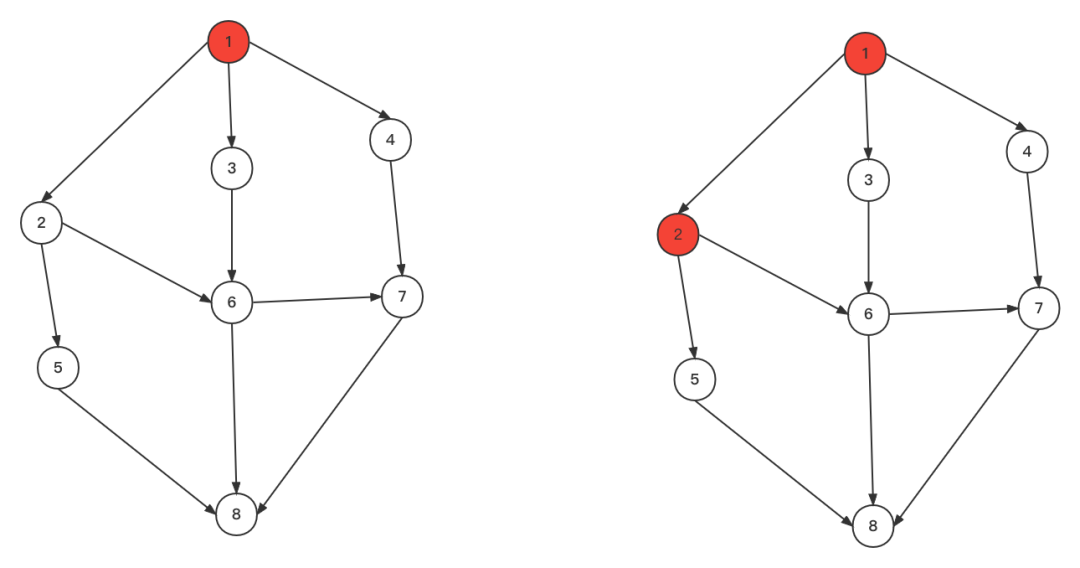2、由顶点2遍历到顶点5，顶点5遍历到顶点8

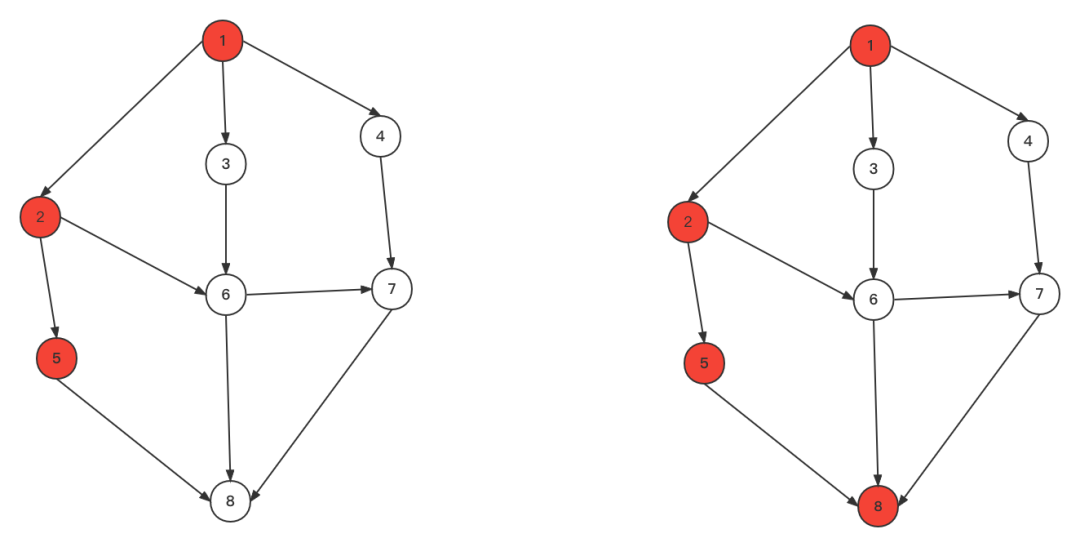3、到顶点8，没有路径回溯到顶点5，然后回溯到顶点2，遍历顶点6， 由顶点6遍历到顶点7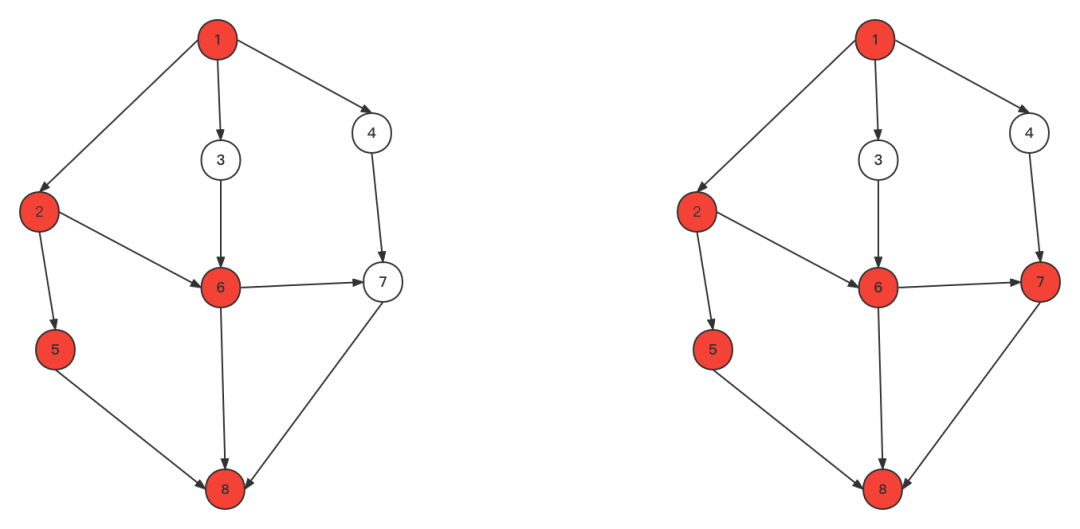4、顶点8已遍历，回溯6，然后回溯到2，然后回溯到1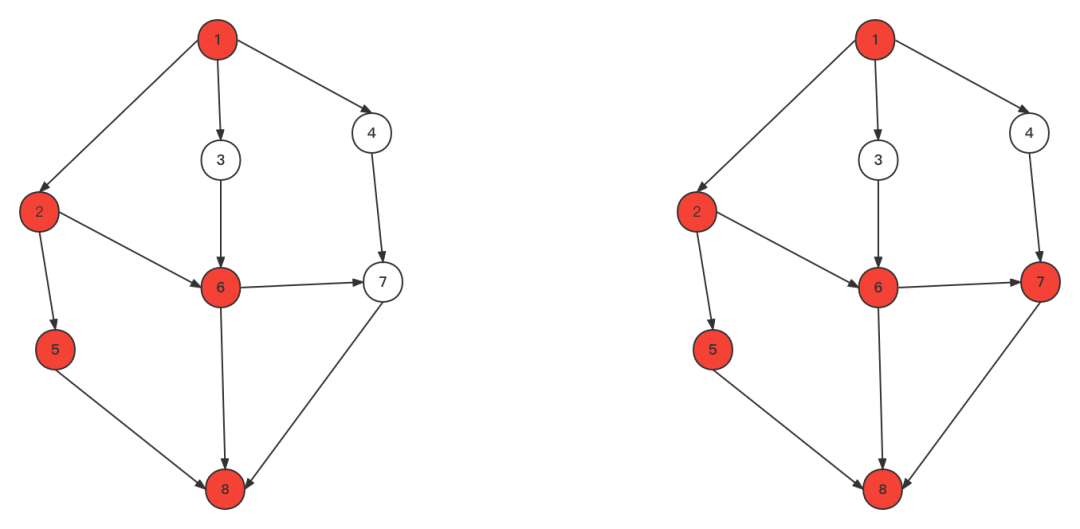5、遍历顶点3，4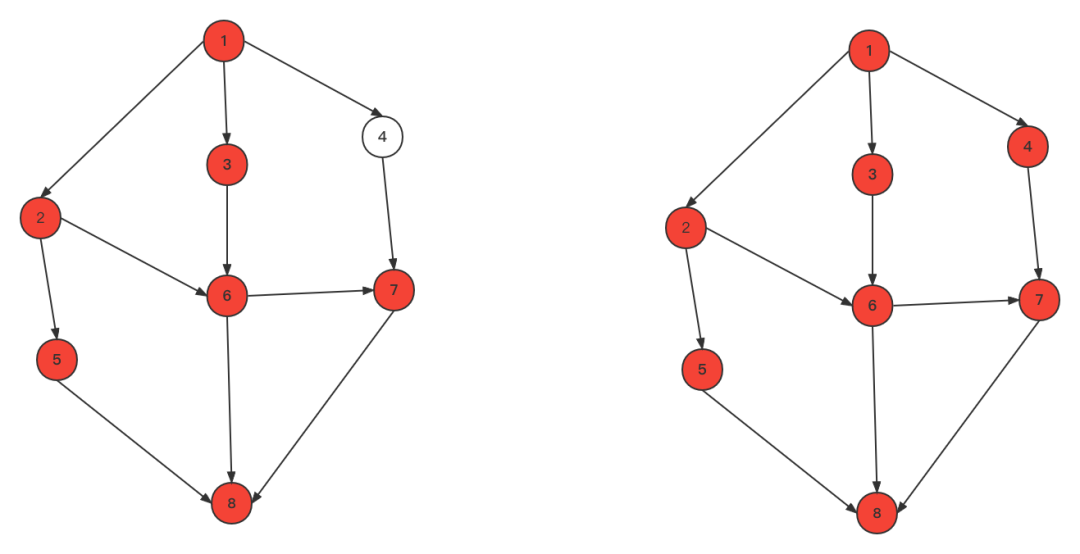

//深搜public void dfsVist(int u){for(int i = posList.get(u).head;i!=-1;i=edgeList.get(i).next){Edge edge = edgeList.get(i);if(!hadVisted[edge.v]){System.out.println("访问节点:"+edge.v);hadVisted[edge.v] =true;vist(edge.v);}}}

广搜

广搜需要一个队列来辅助 从1开始将与1相连的 2，3，4加入队列，同时1出列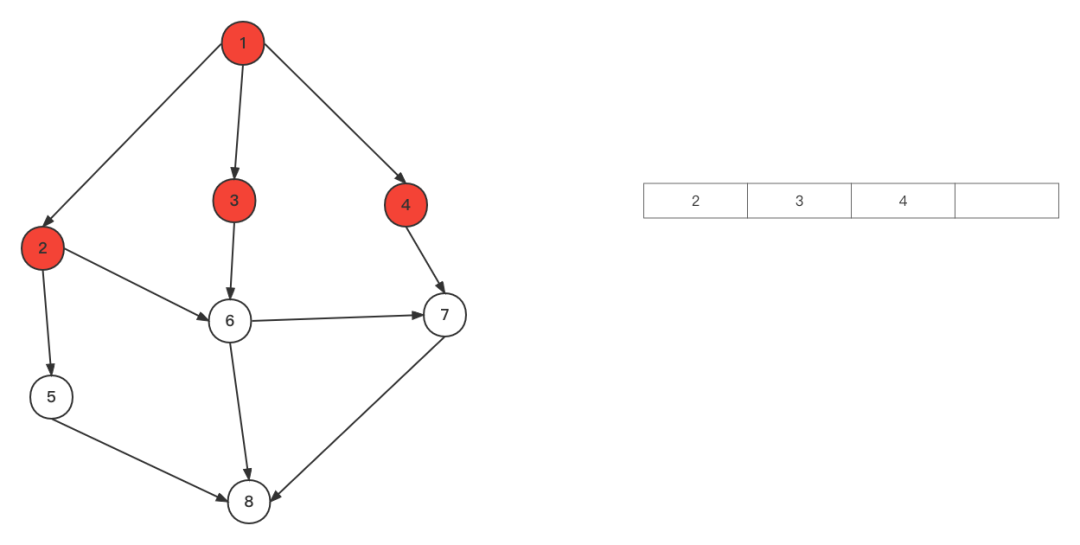从队列开头取出顶点2，将与2相连的5，6加入队列，2出列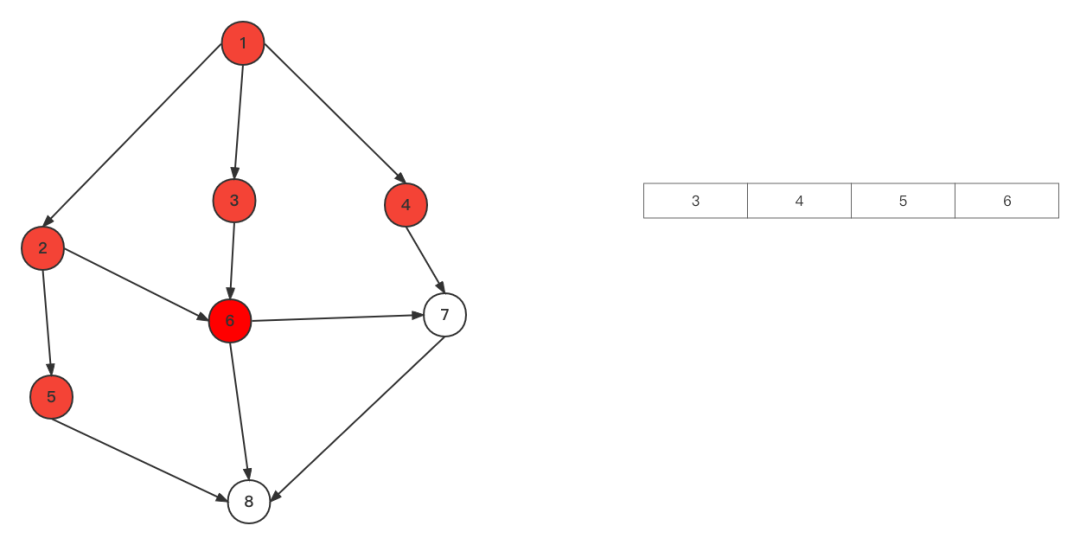取出3，与3相连的都访问了，取出4，3，4出列，7进入队列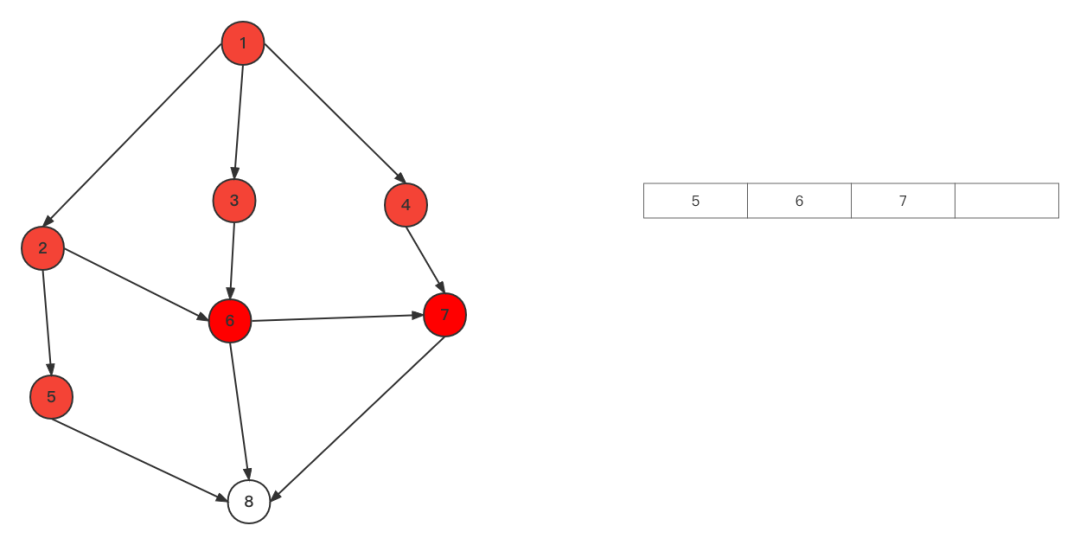取5，将与5相连的8加入队列，5出列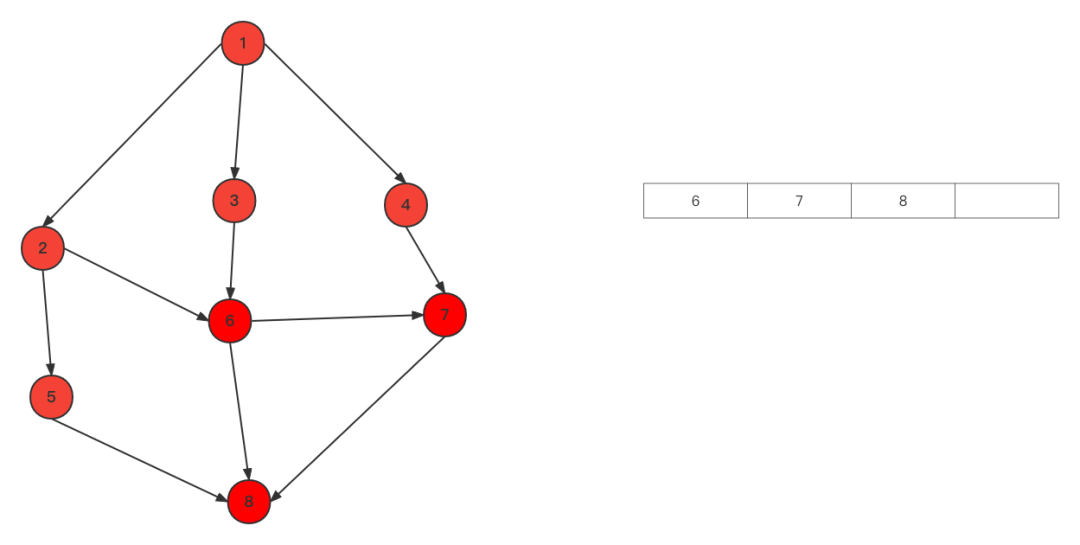接下来取出6，7，8，因为都访问过了，等列表为空，遍历结束

public void bfsVist(int u){Queue queue = new LinkedList();queue.add(u);//加入队列System.out.println("访问节点="+u);while (!queue.isEmpty()){//直至列表为空Integer p = (Integer) queue.poll();//取出列表里元素for(int i = posList.get(p).head;i!=-1;i=edgeList.get(i).next){Edge edge = edgeList.get(i);if(!hadVisted[edge.v]){hadVisted[edge.v] =true;System.out.println("访问节点="+edge.v);queue.add((Integer)edge.v);}}}}

- END -

关于奇舞团

奇舞团是 360 集团最大的大前端团队，代表集团参与 W3C 和 ECMA 会员（TC39）工作。奇舞团非常重视人才培养，有工程师、讲师、翻译官、业务接口人、团队 Leader 等多种发展方向供员工选择，并辅以提供相应的技术力、专业力、通用力、领导力等培训课程。奇舞团以开放和求贤的心态欢迎各种优秀人才关注和加入奇舞团。