什么是url跳转漏洞?
什么是url跳转漏洞
- 简介
- 原因:
- 如何防止
简介
URL跳转漏洞是一种Web应用程序安全问题,指的是在应用程序处理URL跳转时,由于程序员的疏忽或设计不当,攻击者可能通过构造恶意URL来实现对应用程序的攻击。
原因:
-
跳转条件不足:应用程序可能会在没有满足特定条件的情况下进行跳转,这使得攻击者能够利用这个漏洞来执行恶意代码。
-
跳转策略不当:应用程序可能会在没有正确识别请求来源的情况下进行跳转,这可能会导致攻击者能够利用这个漏洞来访问他们原本无法访问的页面或执行他们原本无法执行的操作。
-
跳转参数未过滤:如果应用程序没有正确地过滤掉跳转参数中的恶意代码,攻击者可能会利用这个漏洞来执行恶意代码。
如何防止
URL跳转漏洞是指攻击者通过构造恶意URL,诱导用户点击并跳转到恶意页面,从而实现攻击目的。为了防止URL跳转漏洞,可以采取以下措施:
-
检查输入:在处理用户输入时,要对输入进行严格的验证和过滤。特别是对于可能导致URL跳转的关键字和特殊字符,如“/”、“?”、“#”、“@”、“:”等,要进行过滤或转义。
-
使用白名单策略:只允许已知的、安全的URL跳转。对于未知的URL跳转请求,应禁止访问。
-
限制跳转范围:避免将跳转权限授予不必要的用户或角色。可以设置跳转权限仅对管理员或特定角色开放。
-
使用安全的跳转方法:尽量避免使用HTTP跳转,而使用HTTPS或其他安全协议进行跳转。HTTPS协议可以有效防止中间人攻击和数据窃取。
-
定期更新:确保Web应用程序、框架和库都是最新版本,以修复已知的安全漏洞。
-
对跳转请求进行跟踪和日志记录:监控跳转请求,以便在发现异常行为时迅速采取措施。同时,记录跳转日志,以便在出现问题时进行审计和调查。
-
使用Web应用防火墙(WAF):部署Web应用防火墙,以过滤恶意请求和保护Web应用程序免受攻击。
-
对跳转页面进行安全审查:在跳转到目标页面之前,对跳转页面进行安全审查,以确保其内容的安全性。
-
限制跳转源:限制跳转源,只允许来自可信来源的跳转请求。例如,只允许从特定IP地址、域名或设备进行跳转。
-
使用安全的开发实践:遵循安全的Web开发实践,如使用安全的编程语言、框架和库,以及定期进行代码审查。
通过以上措施,可以有效防止URL跳转漏洞,保护Web应用程序的安全。
相关文章:

什么是url跳转漏洞?
什么是url跳转漏洞 简介原因:如何防止 简介 URL跳转漏洞是一种Web应用程序安全问题,指的是在应用程序处理URL跳转时,由于程序员的疏忽或设计不当,攻击者可能通过构造恶意URL来实现对应用程序的攻击。 原因: 跳转条件…...

生物学经典blast比对算法,R语言和Python如何实现?
Blast比对算法原理与实现方式 做生物的同学肯定听说过blast比对这个方法,一般在NCBI等网站上可以在线进行比对,也可以在本地服务器进行比对,那么blast算法究竟是怎么实现对不同序列的比对呢? 本文分享经典blast算法的基础原理&…...

Android 开机动画支持mp4格式视频播放
前 言 Android系统在启动的过程中,最多可以出现三个画面,每一个画面都用来描述一个不同的启动阶段。无论是哪一个画面,它们都是在一个称为帧缓冲区(frame buffer,简称fb)的硬件设备上进行渲染的。 自定义…...

软考A计划-试题模拟含答案解析-卷十
点击跳转专栏>Unity3D特效百例点击跳转专栏>案例项目实战源码点击跳转专栏>游戏脚本-辅助自动化点击跳转专栏>Android控件全解手册点击跳转专栏>Scratch编程案例 👉关于作者 专注于Android/Unity和各种游戏开发技巧,以及各种资源分享&am…...

Kafka入门(安装和SpringBoot整合)
文章目录 一、Docker安装Kafka1. 创建网络2. 安装zookeeper3. 安装Kafka 二、Kafka介绍1. Kafka简介 三、SpringBoot整合Kafka1. 引入pom依赖2. application.propertise配置3. Hello Kafka(Producer)4. Consumer Kafka5. 带回调的生产者6. 自定义分区器7. kafka事务提交8. 指定…...

gitLab相关命令
gitLab相关命令 1) 远程仓库相关命令 git clone 远程仓库地址 #检出仓库git remote -v #查看远程仓库git remote add [name][url] #添加远程仓库,git remote add origin 远程仓库地址git remote rm [name] #删除远程仓库,git remote rm origingit remo…...

一些查看日志时的常用命令
文章目录 1、grep -r 搜索内容 *2、l * 关键字 *3、tail -f 文件名4、tail -n X 文件名5、cat 文件名 | grep "关键字" -C X同理可得,-A同理可得,-B 一些查看日志时的常用命令 1、grep -r 搜索内容 * 作用:在一堆文件里࿰…...
和作用域(scope)及垃圾回收)
Javascript 的执行环境(execution context)和作用域(scope)及垃圾回收
执行环境有全局执行环境和函数执行环境之分,每次进入一个新执行环境,都会创建一个搜索变量和函数的作用域链。函数的局部环境不仅有权访问函数作用于中的变量,而且可以访问其外部环境,直到全局环境。全局执行环境只能访问全局执行…...

CRDT协同算法
CRDT的英文全称是Conflict-free Replicated Data Type,最初是由协同文本编辑和移动计算而发展的,现在还被用作在线聊天系统、音频分发平台等等。当前CRDT算法在富文本编辑器领域的协同依旧是典型的场景,常用于作为实现文档协同的底层算法&…...

近代中国的三次思想文化运动
1、戊戌变法中维新派顽固派论战 第一次思想解放潮流是1898年维新派与顽固势力的论战。论战的内容有:要不要变法,要不要兴民权、实行君主立宪,要不要提倡西学、改变教育制度。此次论争是资本主义思想同封建主义思想的正面交锋,此后…...

《地铁上的面试题》--目录
第一部分:基础 数据结构与算法 1.1 数组和链表 1.2 栈和队列 1.3 树和图 1.4 排序和搜索算法 1.5 动态规划和贪心算法 操作系统 2.1 进程与线程 2.2 内存管理 2.3 文件系统 2.4 进程同步与通信 2.5 虚拟化和容器化技术 计算机网络 3.1 TCP/IP协议 3.2 HTTP和HTTPS…...

在VIVADO下烧写ZC706板载FLASH的操作步骤
1,原理图分析 首先看原理图,我们兼容ZC706的板子有两片 FLASH,型号是S25FL128A,连接方式如下: 可以看到两片是分别接在了XC7Z045芯片的引脚上,是互不相干的并联方式,每个FLASH芯片支持X4模式,也…...

第二期:链表经典例题(两数相加,删除链表倒数第N个节点,合并两个有序列表)
每道题后都有解析帮助你分析做题,答案在最下面,关注博主每天持续更新。 PS:每道题解题方法不唯一,欢迎讨论! 1.两数相加 题目描述 给你两个非空的链表,表示两个非负的整数。它们每位数字都是按照逆序的方式…...

ESP32设备驱动-SHT35湿度传感器驱动
SHT35湿度传感器驱动 1、SHT35介绍 SHT35 数字温湿度传感器基于 Sensirion SHT35 传感器 IC。 得益于Sensirion的CMOSens技术,高度集成的电容式湿度传感元件和带隙温度传感元件,SHT35具有高可靠性和长期稳定性,功耗低,响应速度快,抗干扰能力强。 传感器支持IIC通信,兼容…...

如何快速判断GitLab 是否出现 OOM
查看系统日志: 使用 dmesg 命令来查看系统日志,搜索 Out of memory 关键字: sudo dmesg | grep -i "out of memory"如果输出结果中包含 Out of memory 或 oom-killer 等关键字,则表示系统出现了 OOM。 查看 GitLab 日…...
)
Word查找和替换通配符(完全版)
Word查找栏代码通配符一览表 序号 清除使用通配符复选框 勾选使用通配符复选框 特殊字符 代码 特殊字符 代码or通配符 1 任意单个字符 ^? 任意单个字符 ? 2 任意数字 ^# 任意数字(单个) [0-9] 3 任意英文字母 ^$ 任意英文字母 [a…...
Linux下socketpair系统API调用使用说明
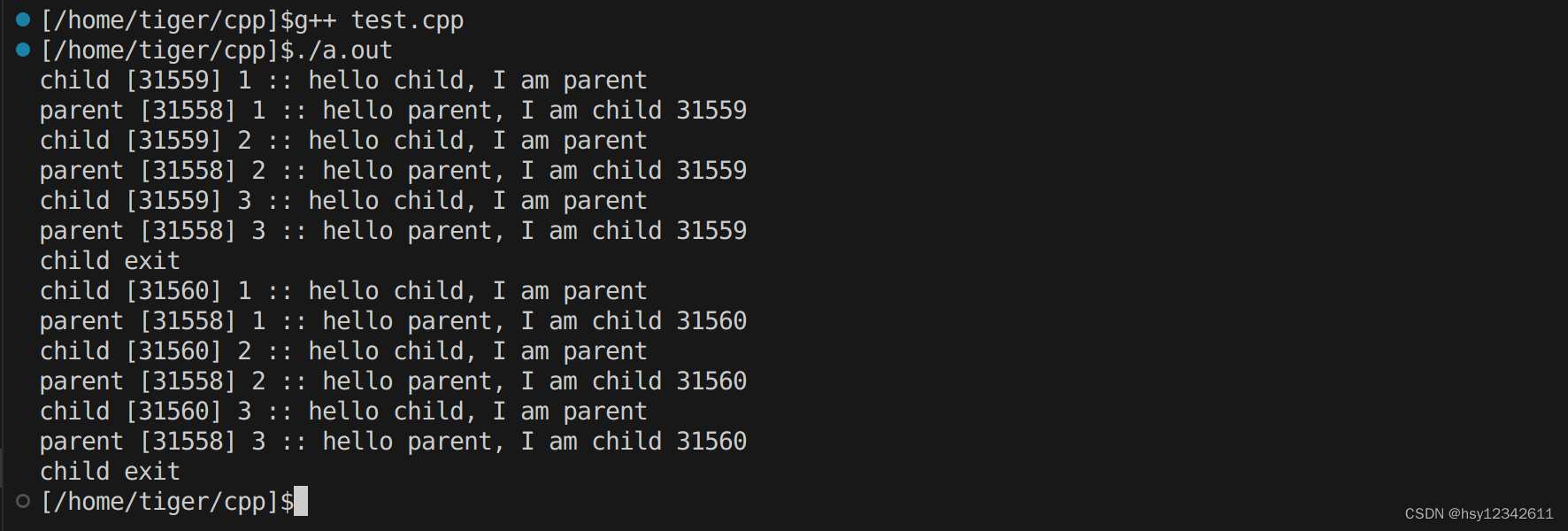
目录 1.socketpair函数说明 2.socketpair使用举例 在阅读nginx源码时,发现其调用socketpair来实现master和worker进程之间进行数据交互。其代码如下: 思考:master和worker进程是父子关系,有亲属关系的进程通过pipe/pipe2&#x…...
)
【Netty】Future 源码分析(十六)
文章目录 前言一、JDK 的 Future 接口二、Netty 的 Future 接口三、ChannelFuture 接口总结 前言 回顾Netty系列文章: Netty 概述(一)Netty 架构设计(二)Netty Channel 概述(三)Netty Channel…...

5月《中国数据库行业分析报告》正式发布,首发时序、实时数据库两大【全球产业图谱】
为了帮助大家及时了解中国数据库行业发展现状、梳理当前数据库市场环境和产品生态等情况,从2022年4月起,墨天轮社区行业分析研究团队出品将持续每月为大家推出最新《中国数据库行业分析报告》,持续传播数据技术知识、努力促进技术创新与行业生…...
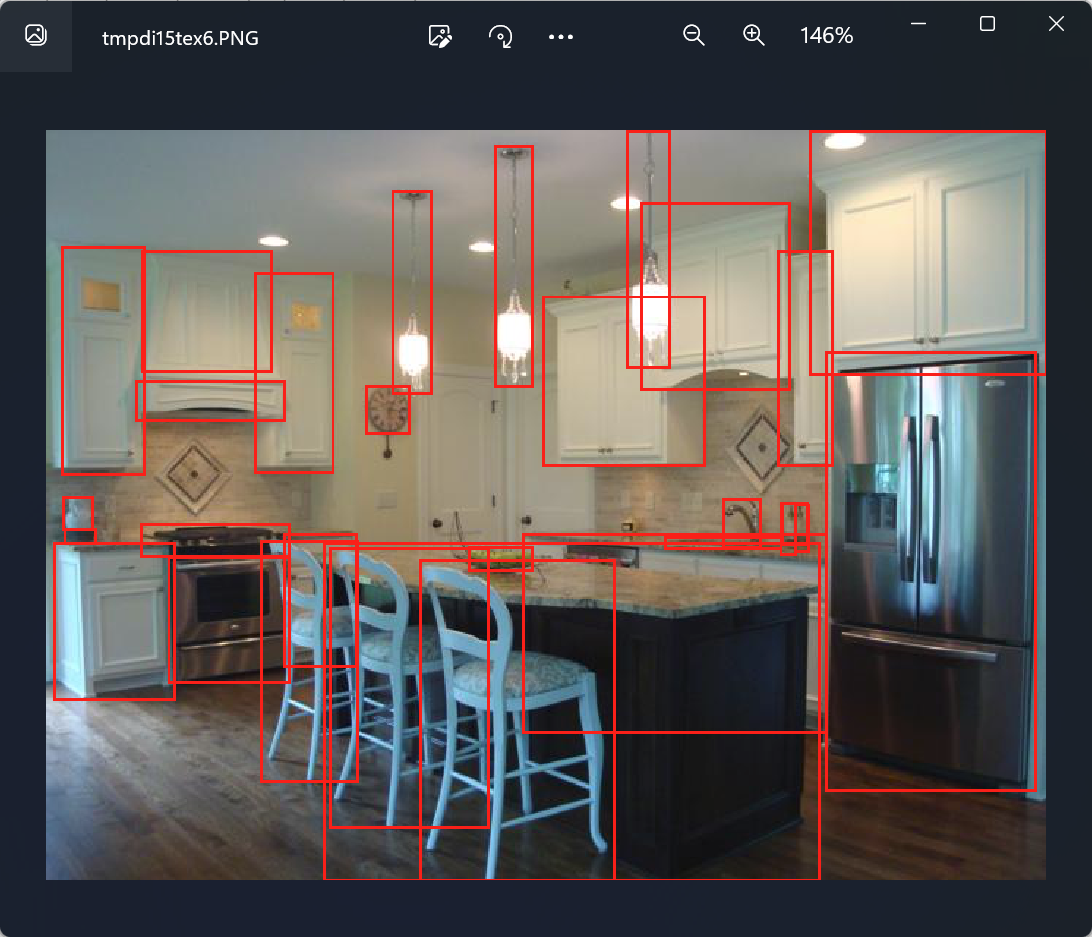
【计算机视觉 | 目标检测】术语理解6:ViT 变种( ViT-H、ViT-L ViT-B)、bbox(边界框)、边界框的绘制(含源代码)
文章目录 一、ViT & ViT变种1.1 ViT的介绍1.2 ViT 的变种 二、bbox(边界框)三、边界框的绘制 一、ViT & ViT变种 1.1 ViT的介绍 ViT,全称为Vision Transformer,是一种基于Transformer架构的视觉处理模型。传统的计算机视…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
