React学习笔记九-高阶函数与函数柯里化
此文章是本人在学习React的时候,写下的学习笔记,在此纪录和分享。此为第九篇,主要介绍高阶函数与函数柯里化。
高阶函数,和函数的柯里化,是学习react的拓展,方便以后优化代码,更好的学习react。
目录
高阶函数
案例
高阶函数定义
函数的柯里化
函数柯里化的定义
柯里化小案例
不用柯里化的写法
高阶函数
案例
先把上一笔记里面的案例,拿出来:这个案例就是,两个输入框分别是用户名和密码,输入用户名和密码,点击登录按钮,会弹出一个提示框,显示你输入的用户名和密码。
<!-- 准备好容器 --><div id="test1"></div><script src="https://cdn.staticfile.org/react/16.4.0/umd/react.development.js"></script><script src="https://cdn.staticfile.org/react-dom/16.4.0/umd/react-dom.development.js"></script><script src="https://cdn.staticfile.org/babel-standalone/6.26.0/babel.min.js"></script><!-- 新引入的库,用于限定props传入值的类型,propTypes --><script src="https://cdn.bootcss.com/prop-types/15.6.1/prop-types.js"></script><script type="text/babel">class Login extends React.Component {//状态初始化state = {username:'',//用户名password:''//密码}//保存用户名到状态中saveUsername = (event)=>{this.setState({username:event.target.value})}//保存密码到状态中savePassword = (event)=>{this.setState({password:event.target.value})}//表单提交的回调handleSubmit = (event) => {event.preventDefault()const {username,password} = this.statealert(`您输入的用户名是${username},输入的密码是${password}`)}render() {return (<form action="http://www.atguigu.com" onSubmit={this.handleSubmit}>用户名:<input onChange = {this.saveUsername} type="text" name="username" />密码:<input onChange = {this.savePassword} type="password" name="password" /><button>登录</button></form>)}}ReactDOM.render(<Login />, document.getElementById('test1'))</script>如代码所示,表单中需要获取用户名和密码,并且加以操作,所以有了对应的两个方法:saveUsername和savePassword。但如果还存在性别,年龄,电话号码等等信息需要操作,是不是得一一对应,写很多方法?实在是过于冗余,有没有什么解决的办法?
所以我们只写一个方法saveFormData来代替saveUsername和savePassword,来给表单中所有的属性使用:
用户名:<input onChange = {this.saveFormData("username")} type="text" name="username" />密码:<input onChange = {this.saveFormData("password")} type="password" name="password" />saveFormData = (event)=>{this.setState({password:event.target.value})
}但是,这会出现很大的错误。注意onchange的回调函数,它非是一个函数进行了回调,而是一个函数的返回结果进行了回调:this.saveFormData("username"),saveFormData加了小括号,已经在回调时执行完了,产生了函数的返回值,这个返回值参与了回调,就会发生错误。
必须将一个函数返回给onchange作为回调。
如下的写法,才是onchange事件触发时候,回调saveFormData这个函数。
<input onChange = {this.saveFormData} 而且这个saveFromData函数,this.setState也会一直把数据给password。我们接下来修改这些错误。
那么怎么才能在加()的情况下,也能正确执行回调函数呢。众所周知函数加了()就是执行函数产生返回值,那么我们直接让返回值是一个函数不就行了。
改写这个saveFromData函数:
//保存表单数据到状态中
saveFormData = (dataType) => {return (event) => {this.setState({[dataType]: event.target.value})}
}我们将saveFromData函数的返回值,写成了一个函数。如此一来,onchange事件触发后,回调saveFromData函数的返回值,仍然是一个函数,便能达到正常的效果。
我们在onChange={this.saveFormData("username")}中传入参数,在saveFromData函数设置形参dataType接收这个参数,在this.setState中以中括号包裹形参(中括号表示其中是是一个变量,不写中括号会当作一个键名),设置state,这样就可以区分数据,在state中分开保存不同的数据。
来看效果:

高阶函数定义
高阶函数:如果一个函数符合下面两个规范中的任何一个,那该函数就是高阶函数。
1.若A函数,接收的参数是一个函数,那么A就可以被称为高阶函数。
2.若A函数,调用的返回值依然是一个函数,那么A就可以被称为高阶函数。
由此可见:saveFromData函数就是一个高阶函数,调用的返回值是一个函数。
常见的高阶函数,如promise,数组迭代的那几种方法,定时器。
函数的柯里化
函数柯里化的定义
函数的柯里化:通过函数调用继续返回函数的方式,实现多次接收参数最后统一处理的函数编码形式。
柯里化小案例
为了理解柯里化,我们先正常的写一个普通函数的案例:a,b,c 的求和
function sum(a,b,c){return a+b+c}const result = sum(1,2,3)console.log(result);现在把上面的案例,改成柯里化的写法:
function sum(a) {return (b) => {return (c) => {return a + b + c}}}const result = sum(1)(2)(3)console.log(result);这个案例里面的函数柯里化,看似把简单的问题复杂化,变得麻烦,又有些回调地狱的风格。但实际应用上,函数柯里化经常使用。比如说第一个案例,里面的saveFromData函数:
saveFormData = (dataType) => {return (event) => {this.setState({[dataType]: event.target.value})}}先接收了参数dataType,然后再接收了event参数,在后面对两个参数统一处理了,这就是函数的柯里化。
不用柯里化的写法
如果我们不用柯里化的写法,这就要求我们一次性拿到所有参数。主要是在onchange事件里,想办法把两个参数一次性给saveFromData函数传过去。
给onchange事件回调的,必须是一个函数。我们尝试写一个内联函数,这样既能在内联函数中把参数传递给saveFromData函数,又可以保证是一个函数回调给事件。
如下:onChange={(event)=>{this.saveFormData('username',event.target.value)}}
用户名:<input onChange={(event)=>{this.saveFormData('username',event)}} type="text" name="username" />
密码:<input onChange={(event)=>{this.saveFormData('password',event)}} type="password" name="password" />然后我们就可以把saveFromData函数改写成一个普通的函数:
saveFormData = (dataType, event) => {this.setState({[dataType]: event.target.value})}如此,我们改写了这两个部分,就可以把柯里化写法,改成普通的函数写法。
相关文章:

React学习笔记九-高阶函数与函数柯里化
此文章是本人在学习React的时候,写下的学习笔记,在此纪录和分享。此为第九篇,主要介绍高阶函数与函数柯里化。 高阶函数,和函数的柯里化,是学习react的拓展,方便以后优化代码,更好的学习react。…...

2023年电工杯B题半成品论文使用讲解
注:蓝色字体为说明备注解释字体,不能出现在大家的论文里。黑色字体为论文部分,大家可以根据红色字体的注记进行摘抄。该文件为半成品论文,即引导大家每一步做什么,怎么做,展示按着本团队的解题思路进行建模…...
第1关:ODBC程序设计
第1关:ODBC程序设计 任务描述相关知识ODBC主要功能ODBC接口主要函数ODBC应用程序开发实例DM ODBC应用程序开发总体流程DM ODBC代码编写流程DM ODBC代码编写实例 编程要求测试说明代码参考: 任务描述 本关任务:使用 ODBC 查询表中数据。 相关…...
Kotlin笔记(零)简介
百度百科简介 2017年,google公司在官网上宣布Kotlin成为Android的开发语言,使编码效率大增。Kotlin 语言由 JetBrains 公司推出,这是一个面向JVM的新语言 参考资料 官网:https://kotlinlang.org/中文官网:https://w…...

android 12.0去掉usb授权提示框 默认给予权限
1.概述 在12.0的系统rom产品开发中,在进行iot开发过程中,在插入usb设备时会弹出usb授权提示框,也带来一些不便,这个需要默认授予USB权限,插拔usb都不弹出usb弹窗所以这要从usb授权相关管理页默认给与usb权限 2.去掉usb授权提示框 默认给予权限的相关代码 frameworks/bas…...

工作积极主动分享,善于业务沟通
工作积极主动分享,善于业务沟通 目录概述需求: 设计思路实现思路分析1.工作积极主动承担责任2.善于沟通3.一起常常lauch 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy,…...
 : opencv的数据结构)
Opencv-C++笔记 (1) : opencv的数据结构
文章目录 一、OPNECV元素1.CvPoint2、模板类Size模版类Rect模版类RotatedRect模版类 二、MAT1.使用(nrows, ncols, type),初始化2维矩阵如果需要深拷贝,则使用clone方法。 三、Vec类 一、OPNECV元素 1.CvPoint 为了方便使用,opencv又对常用的…...
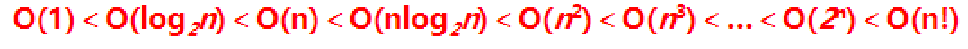
什么是时间复杂度?
时间复杂度定义:在计算机科学中,时间复杂性,又称时间复杂度,算法的时间复杂度是一个函数,它定性描述该算法的运行时间。这是一个代表算法输入值的的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的…...
Spring框架中有哪些不同类型的事件
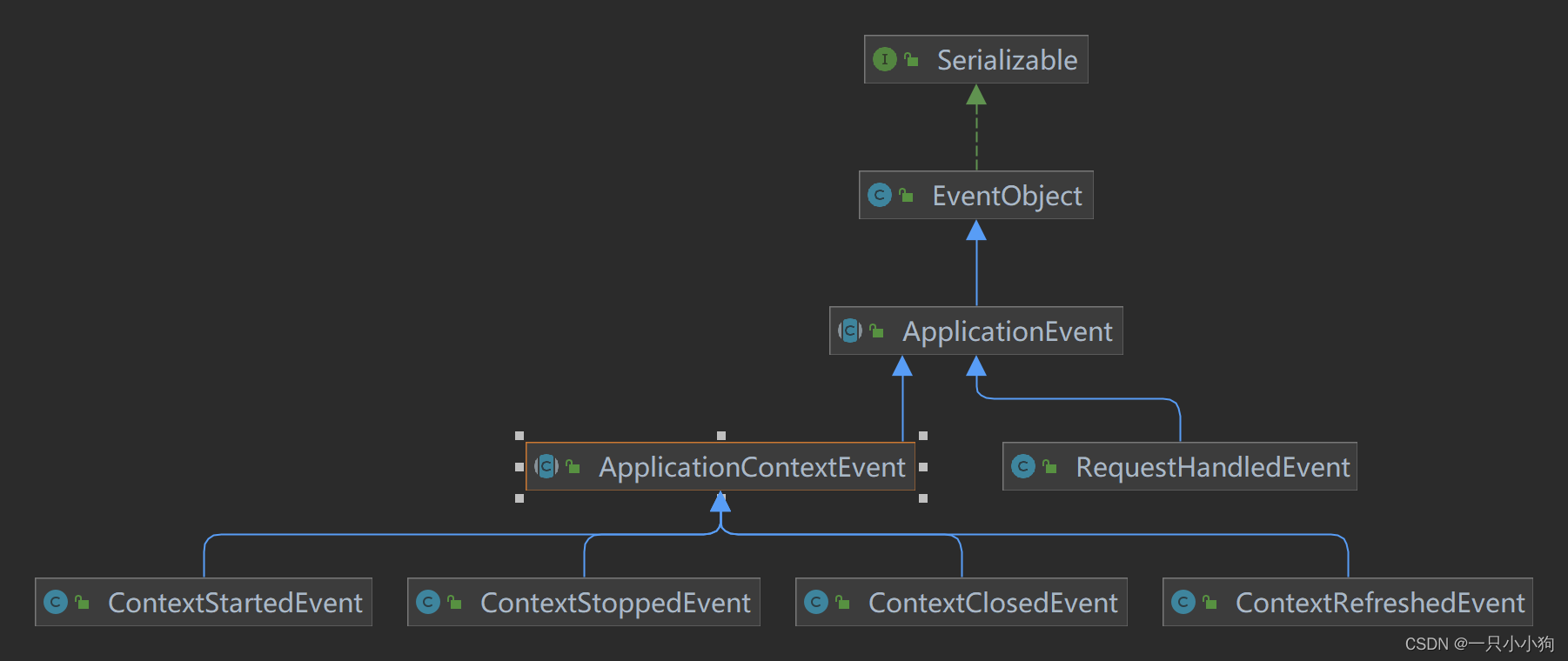
Spring框架中有哪些不同类型的事件 Spring框架中有哪些不同类型的事件 Spring框架中有哪些不同类型的事件 Spring 提供了以下5种标准的事件: 上下文更新事件(ContextRefreshedEvent):在调用ConfigurableApplicationContext 接口…...

Codeforcs 1732C2 暴力
题意 传送门 Codeforcs 1732C2 题解 方便起见,区间表示为左闭右开。观察到 f ( l , r ) ≥ f ( l ′ , r ′ ) , [ l ′ , r ′ ) ∈ [ l , r ) f(l,r)\geq f(l,r),[l,r)\in [l,r) f(l,r)≥f(l′,r′),[l′,r′)∈[l,r),满足单调性,则 […...

Python安全和防护:如何保护Python应用程序和用户数据的安全
章节一:引言 在当今数字化时代,数据安全是一个极其重要的话题。随着Python的广泛应用和越来越多的人使用Python构建应用程序,保护Python应用程序和用户数据的安全变得尤为重要。本文将介绍一些关键的Python安全问题,并提供一些保…...
[转载]Nginx 使用 X-Accel-Redirect 实现静态文件下载的统计、鉴权、防盗链、限速等
需求 统计静态文件的下载次数;判断用户是否有下载权限;根据用户指定下载速度;根据Referer判断是否需要防盗链;根据用户属性限制下载速度; X-Accel-Redirect This allows you to handle authentication, logging or …...

继电器的详细分类
继电器的分类方法较多,可以按作用原理、外形尺寸、保护特征、触点负载、产品用途等分类。 一、按作用原理分 1.电磁继电器 在输入电路内电流的作用下,由机械部件的相对运动产生预定响应的一种继电器。 它包括直流电磁继电器、交流电磁继电器、…...

docker的底层原理,带你上天
1、docker的层级怎么看 先查看当前机器上有哪些镜像 docker images 这里选看mysql的层级 docker image inspect mysql:5.7.29 命令。其中RootFS部分则是表示了分层信息。 2、查看docker的系统信息 因为这台机器的docker不是我安装的,所以不知道具体的根目录在哪里…...
HNU-电子测试平台与工具2-串口实验5次
计算机串口使用与测量 【实验属于电子测试平台与工具】 湖南大学信息科学与工程学院 计科 210X wolf (学号 202108010XXX) 0.环境搭建 在实验开始之前,安装好Ubuntu 20.04操作系统。(这个没有难度) 但要提醒的是,这个ubuntu是xubuntu,而且虚拟硬盘只有10GB的大小…...
Ext JS嵌套分组表格的实现
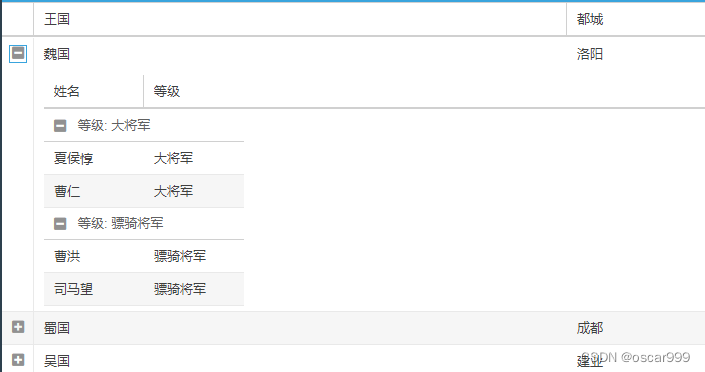
这里的嵌套分组表格指的是这样一种表格 表格的每一行可以展开下一层的Grid展开的嵌套表格是一个分组的表格显示的效果如下图: 这种显示的方式可以显示 3个层级的数据,比如这里的国家 、 将军等级、将军信息。 如果最外层再使用分组的表格, 则可以显示 4个层级的信息, 这种…...
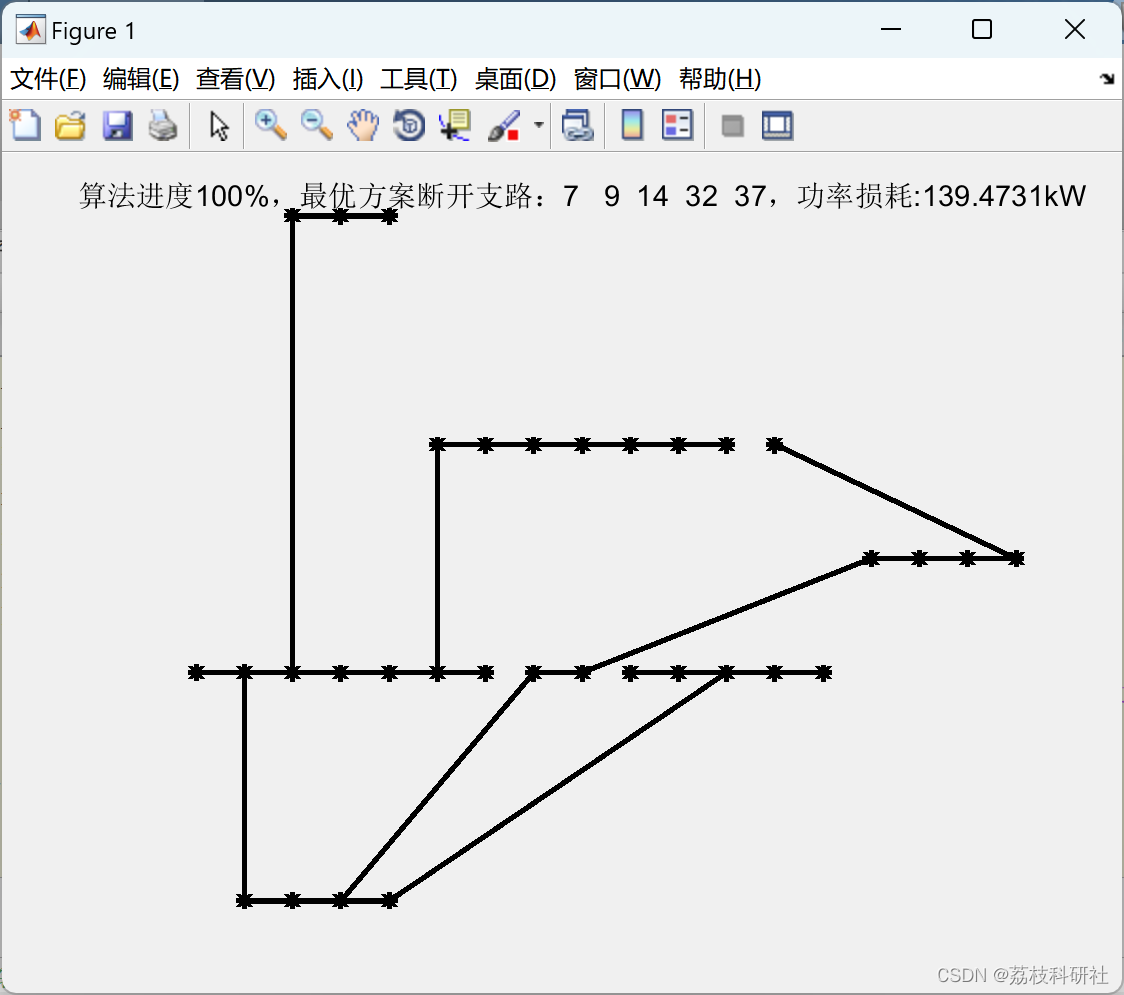
【配电网重构】基于改进二进制粒子群算法的配电网重构研究(Matlab代码实现
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Python编程语言简介
Python 是荷兰人 Guido van Rossum (吉多范罗苏姆,中国程序员称其为“龟叔”)在 1990 年初开发的一种解释型编程语言。 Python 的诞生是极具戏曲性的,据 Guido 自述记载,Python 语言是在圣诞节期间为了打发无聊的时间…...

ChatGPT国内免费访问
背景 ChatGPT作为一种基于人工智能技术的自然语言处理工具,近期的热度直接沸腾🌋。 作为一个程序员,我也忍不住做了一个基于ChatGPT的网站,免费!免梯子!!国内可直接对话ChatGPT,也…...

从零到无搭建Vue项目及代码风格规范
注:已经有vue项目的可以跳过项目初始化 Vue项目搭建 环境搭建 安装nvm 方便后续切换不通的node版本 nvm官网 傻瓜安装就行 或者搜下自己(非本文重点)nvm 安装好后 安装一个Node版本 本文使用的 有了环境开始创建Vue项目 打开命令行 cmd n…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...
