什么是时间复杂度?
时间复杂度定义:在计算机科学中,时间复杂性,又称时间复杂度,算法的时间复杂度是一个函数,它定性描述该算法的运行时间。这是一个代表算法输入值的的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,亦即考察输入值大小趋近无穷时的情况。
时间复杂度
时间复杂度是算法执行时间随输入规模增长而增长的量度,通常用大 O 记号表示。它反映了算法在解决问题时所耗费的时间资源,也可以理解为算法的运行效率。时间复杂度分析的目的是确定算法执行时间与输入规模之间的关系,并帮助我们选择更高效的算法来解决问题。
提到时间复杂度,第一时间想到的是算法,简单说,算法就是你解决问题的方法,而你用这个方法解决这个问题所执行的语句次数,称为语句频度或者时间频度,记为T(n)。
那么问题来了,我们为什么要引入这些个概念呢。因为我们想要的是执行一个算法耗费的时间,这个时间理论上可以得到,但是,要得到这个时间就必须要上机测试,但是有这个必要吗?我们需要知道的是哪一个算法需要的时间多,哪一个算法需要的时间少,这样就可以了。而且,算法的耗时和语句的执行次数是成正比的,即语句执行越多,耗时越多。这也就是我们引入概念的原因。
在上面提到的时间频度T(n)中,n是指算法的规模,n不断的变化,T(n)就会不断的变化,而这些变化的规律是怎样的呢?于是我们引入了时间复杂度的概念。
什么是时间复杂度,算法中某个函数有n次基本操作重复执行,用T(n)表示,现在有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n)) 为算法的渐进时间复杂度,简称时间复杂度。通俗一点讲,其实所谓的时间复杂度,就是找了一个同样曲线类型的函数f(n)来表示这个算法的在n不断变大时的趋势 。当输入量n逐渐加大时,时间复杂性的极限情形称为算法的“渐近时间复杂性”。
我们用大O表示法表示时间复杂性,它是一个算法的时间复杂性。大O表示只是说有上界但并不是上确界。
“大O记法”:在这种描述中使用的基本参数是 n,即问题实例的规模,把复杂性或运行时间表达为n的函数。这里的“O”表示量级 (order),比如说“二分检索是 O(logn)的”,也就是说它需要“通过logn量级的步骤去检索一个规模为n的数组”记法 O ( f(n) )表示当 n增大时,运行时间至多将以正比于 f(n)的速度增长。
时间复杂度对于算法进行的分析和大致的比较非常有用,但是真正的情况可能会因为一些其他因素造成差异。比如一个低附加代价的O(n2)算法在n较小的情况下可能比一个高附加代价的 O(nlogn)算法运行得更快。但是,n越来越大以后,相比较而言较慢上升函数的算法会运行的更快。
时间复杂度是渐进的
常见的时间复杂度有:O(1)、O(log n)、O(n)、O(n log n)、O(n²) 等。其中,O(1) 表示算法的执行时间不随输入规模增长而增长;O(log n) 表示算法的执行时间随输入规模增长而增长,但增长速度非常缓慢;O(n) 表示算法的执行时间与输入规模成线性增长关系;O(n log n) 表示算法的执行时间随输入规模增长而增长,并且增长速度介于线性和平方之间;O(n²) 表示算法的执行时间随输入规模增长而呈现平方级别的增长。
在实际的算法设计和分析中,我们通常关注最坏情况下的时间复杂度,即算法在处理最难的输入时所需的时间。
如果我们将算法中的一次计算记为 1,那么如果有 n 个输入值,算法对每一个输入值做一次运算,那么整个算法的运算量即为 n。这个时候,我们就可以说,这是一个时间复杂度为 O(n) 的算法。
同理,如果仍有 n个输入值,但算法对每一个输入值做一次运算这个操作需要再重复n次,那么整个算法的运算量即为n*n = n^2,时间复杂度为 O(n^2) 。
这时如果对每一个输入值做一次运算,而这个操作需要重复n+1次,算法运算量变为:
n(n+1) = n^2 + n。
这时的时间复杂度是否改变为O(n^2+n)呢?
上文曾提到时间复杂度考察的是当输入量趋于无穷时的情况,所以当 n趋于无穷的时候,n^2 对算法运行时间占主导地位,而 n 在 n^2 面前就无足轻重,不计入时间复杂度中。
换句话说,因为n^2 + n渐近地(在取极限时)与 n^2相等。此外,就运行时间来说,n 前面的常数因子远没有输入规模 n的依赖性重要,所以是可以被忽略的,也就是说O(n^2)和 是O(n^2/2)相同时间复杂度的,都为O(n^2)。
简单算法的时间复杂度举例
O(1)的算法是一些运算次数为常数的算法。例如:
temp=a;a=b;b=temp;
上面语句共三条操作,单条操作的频度为1,即使他有成千上万条操作,也只是个较大常数,这一类的时间复杂度为O(1)。
O(n)的算法是一些线性算法。例如:
sum=0;
for(i=0;i<n;i++)
sum++;
上面代码中第一行频度1,第二行频度为n,第三行频度为n,所以f(n)=n+n+1=2n+1。所以时间复杂度O(n)。这一类算法中操作次数和n正比线性增长。
O(logn) 一个算法如果能在每个步骤去掉一半数据元素,如二分检索,通常它就取 O(logn)时间。举个栗子:
int i=1;
while (i<=n)
i=i*2;
上面代码设第三行的频度是f(n), 则:2的f(n)次方<=n;f(n)<=log₂n,取最大值f(n)= log₂n,所以T(n)=O(log₂n ) 。
O(n²)(n的k次方的情况)最常见的就是平时的对数组进行排序的各种简单算法都是O(n²),例如直接插入排序的算法。
而像矩阵相乘算法运算则是O(n³)。
举个简单栗子:
sum=0;
for(i=0;i<n;i++)
for(j=0;j<n;j++)
sum++;
第一行频度1,第二行n,第三行n²,第四行n²,T(n)=2n²+n+1 =O(n²)
O(2的n次方) 比如求具有n个元素集合的所有子集的算法
O(n!) 比如求具有N个元素的全排列的算法
时间复杂度按n越大算法越复杂来排的话:常数阶O(1)、对数阶O(logn)、线性阶O(n)、线性对数阶O(nlogn)、平方阶O(n²)、立方阶O(n³)、……k次方阶O(n的k次方)、指数阶O(2的n次方)。
借用别人的图:
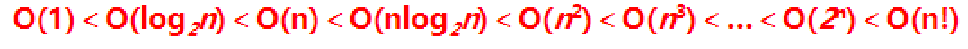
总结
时间复杂度是一个衡量算法运行效率的概念,表示随着问题规模n的增加,算法所需的执行时间的增速。一般用大O符号来表示,称为“大O记号”,如O(1)、O(log n)、O(n)、O(n log n)等。
不同的算法在处理同一问题时,其时间复杂度可以有明显的差异,因此选择高效的算法对于解决大规模数据问题时尤为重要。
时间复杂度的目的是为了帮助我们在实际开发中,选择更优秀的算法来解决具有不同规模的问题。因为对于大规模的问题,其时间复杂度的差异会直接影响到算法的实际执行效率。因此,我们需要在算法设计时考虑时间复杂度,选择最优的算法来处理实际的问题。
需要注意的是,时间复杂度并非表示具体的执行时间,而是代表了算法执行时间和输入规模之间的关系,因此只能用于算法之间的比较,不能直接用于预测算法的实际执行时间。
相关文章:
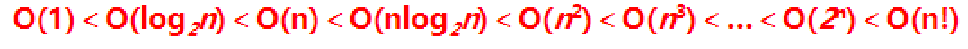
什么是时间复杂度?
时间复杂度定义:在计算机科学中,时间复杂性,又称时间复杂度,算法的时间复杂度是一个函数,它定性描述该算法的运行时间。这是一个代表算法输入值的的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的…...
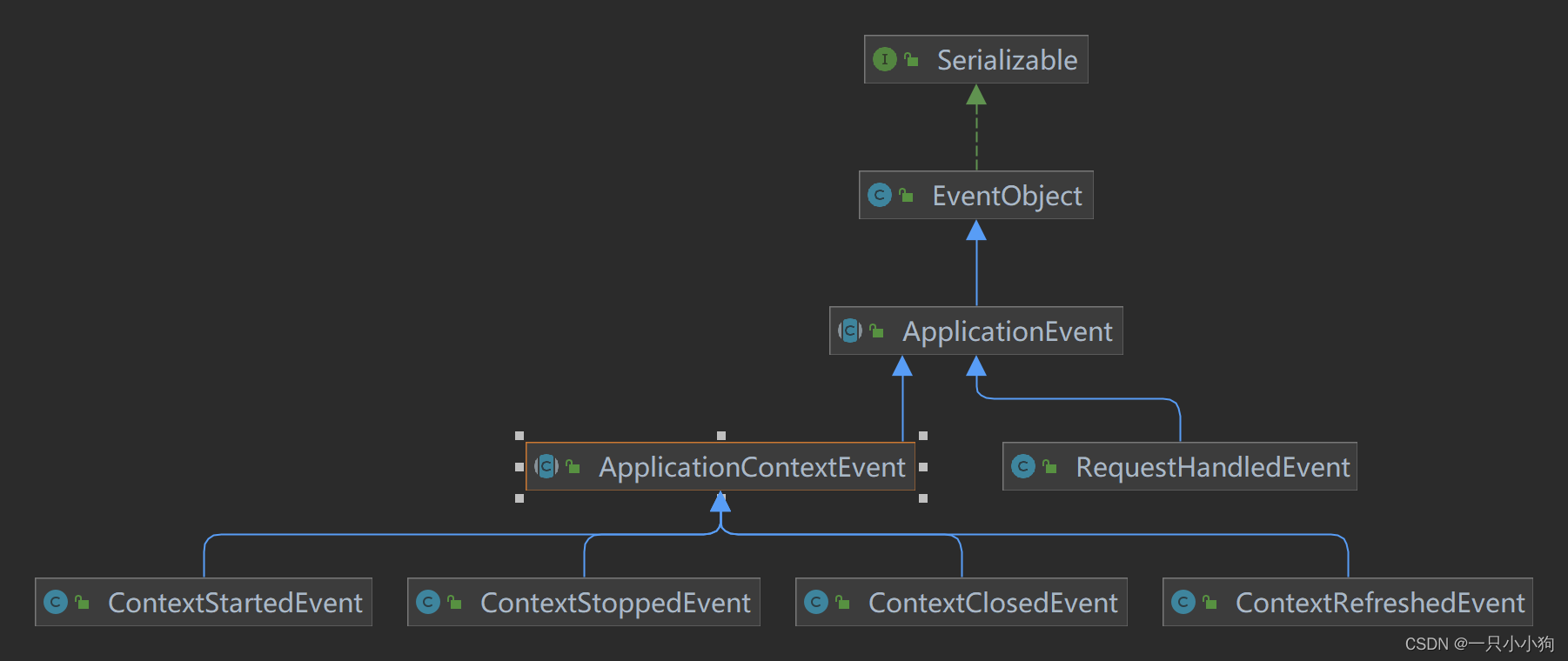
Spring框架中有哪些不同类型的事件
Spring框架中有哪些不同类型的事件 Spring框架中有哪些不同类型的事件 Spring框架中有哪些不同类型的事件 Spring 提供了以下5种标准的事件: 上下文更新事件(ContextRefreshedEvent):在调用ConfigurableApplicationContext 接口…...

Codeforcs 1732C2 暴力
题意 传送门 Codeforcs 1732C2 题解 方便起见,区间表示为左闭右开。观察到 f ( l , r ) ≥ f ( l ′ , r ′ ) , [ l ′ , r ′ ) ∈ [ l , r ) f(l,r)\geq f(l,r),[l,r)\in [l,r) f(l,r)≥f(l′,r′),[l′,r′)∈[l,r),满足单调性,则 […...

Python安全和防护:如何保护Python应用程序和用户数据的安全
章节一:引言 在当今数字化时代,数据安全是一个极其重要的话题。随着Python的广泛应用和越来越多的人使用Python构建应用程序,保护Python应用程序和用户数据的安全变得尤为重要。本文将介绍一些关键的Python安全问题,并提供一些保…...
[转载]Nginx 使用 X-Accel-Redirect 实现静态文件下载的统计、鉴权、防盗链、限速等
需求 统计静态文件的下载次数;判断用户是否有下载权限;根据用户指定下载速度;根据Referer判断是否需要防盗链;根据用户属性限制下载速度; X-Accel-Redirect This allows you to handle authentication, logging or …...

继电器的详细分类
继电器的分类方法较多,可以按作用原理、外形尺寸、保护特征、触点负载、产品用途等分类。 一、按作用原理分 1.电磁继电器 在输入电路内电流的作用下,由机械部件的相对运动产生预定响应的一种继电器。 它包括直流电磁继电器、交流电磁继电器、…...

docker的底层原理,带你上天
1、docker的层级怎么看 先查看当前机器上有哪些镜像 docker images 这里选看mysql的层级 docker image inspect mysql:5.7.29 命令。其中RootFS部分则是表示了分层信息。 2、查看docker的系统信息 因为这台机器的docker不是我安装的,所以不知道具体的根目录在哪里…...
HNU-电子测试平台与工具2-串口实验5次
计算机串口使用与测量 【实验属于电子测试平台与工具】 湖南大学信息科学与工程学院 计科 210X wolf (学号 202108010XXX) 0.环境搭建 在实验开始之前,安装好Ubuntu 20.04操作系统。(这个没有难度) 但要提醒的是,这个ubuntu是xubuntu,而且虚拟硬盘只有10GB的大小…...
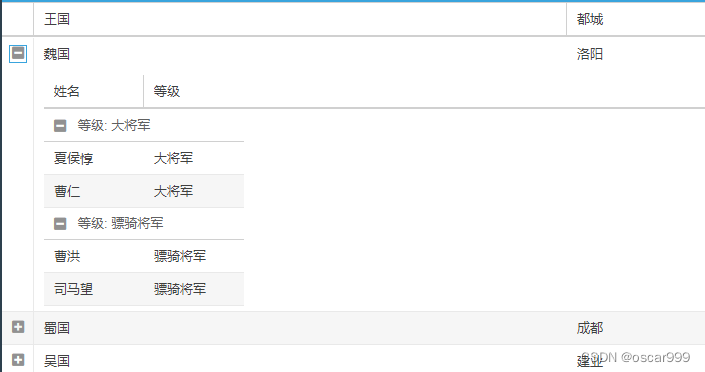
Ext JS嵌套分组表格的实现
这里的嵌套分组表格指的是这样一种表格 表格的每一行可以展开下一层的Grid展开的嵌套表格是一个分组的表格显示的效果如下图: 这种显示的方式可以显示 3个层级的数据,比如这里的国家 、 将军等级、将军信息。 如果最外层再使用分组的表格, 则可以显示 4个层级的信息, 这种…...
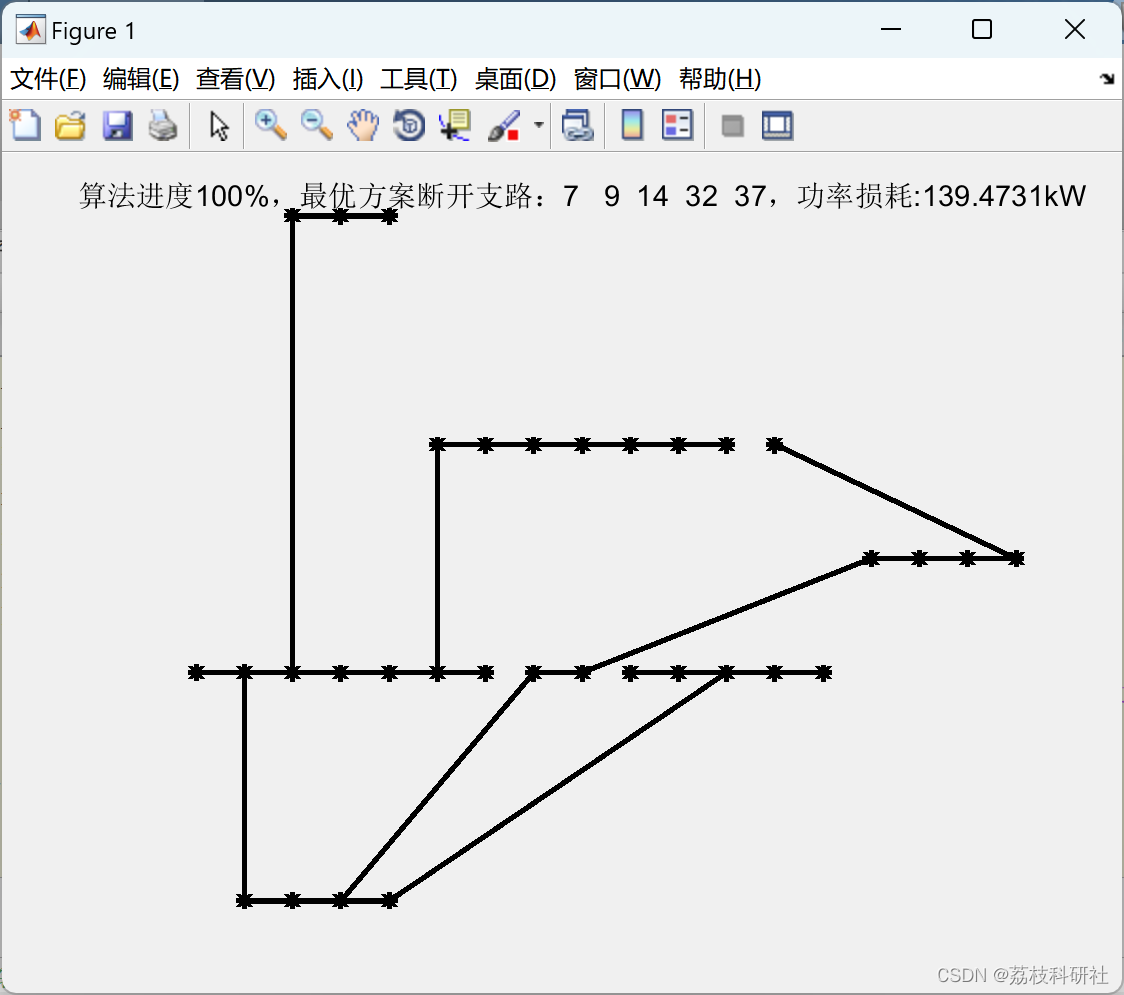
【配电网重构】基于改进二进制粒子群算法的配电网重构研究(Matlab代码实现
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Python编程语言简介
Python 是荷兰人 Guido van Rossum (吉多范罗苏姆,中国程序员称其为“龟叔”)在 1990 年初开发的一种解释型编程语言。 Python 的诞生是极具戏曲性的,据 Guido 自述记载,Python 语言是在圣诞节期间为了打发无聊的时间…...

ChatGPT国内免费访问
背景 ChatGPT作为一种基于人工智能技术的自然语言处理工具,近期的热度直接沸腾🌋。 作为一个程序员,我也忍不住做了一个基于ChatGPT的网站,免费!免梯子!!国内可直接对话ChatGPT,也…...

从零到无搭建Vue项目及代码风格规范
注:已经有vue项目的可以跳过项目初始化 Vue项目搭建 环境搭建 安装nvm 方便后续切换不通的node版本 nvm官网 傻瓜安装就行 或者搜下自己(非本文重点)nvm 安装好后 安装一个Node版本 本文使用的 有了环境开始创建Vue项目 打开命令行 cmd n…...
)
ASP.NET基于BS结构的实验室预约模型系统(源代码+论文)
《基于B/S结构的实验室预约模型系统》是采用ASP.NET开发的一个开放实验室预约系统。本系统是针对目前实验室手工管理效率低下,缺乏安全性、可控性等缺点,以校园网为依托,采用科学、高效的教学管理方式,使学校的教学资源得到充分的利用。本系统主要实现了教师根据实际教学情…...

Java货运物流园管理系统源码
技术架构:spring boot、mybatis、redis、vue、element-ui 开发语言:java、vue、uniapp 开发工具:idea、vscode、hbuilder 前端框架:vue 后端框架:spring boot 数 据 库:mysql 移 动 端: …...
Linux4.2LAMP
文章目录 计算机系统5G云计算第一章 LINUX LAMP一、概述二、编译安装Apache httpd服务1.关闭防火墙,将安装Apache所需软件包传到/opt目录下2.安装环境依赖包3.配置软件模块4.编译及安装5.优化配置文件路径,并把httpd服务的可执行程序文件放入路径环境变量…...
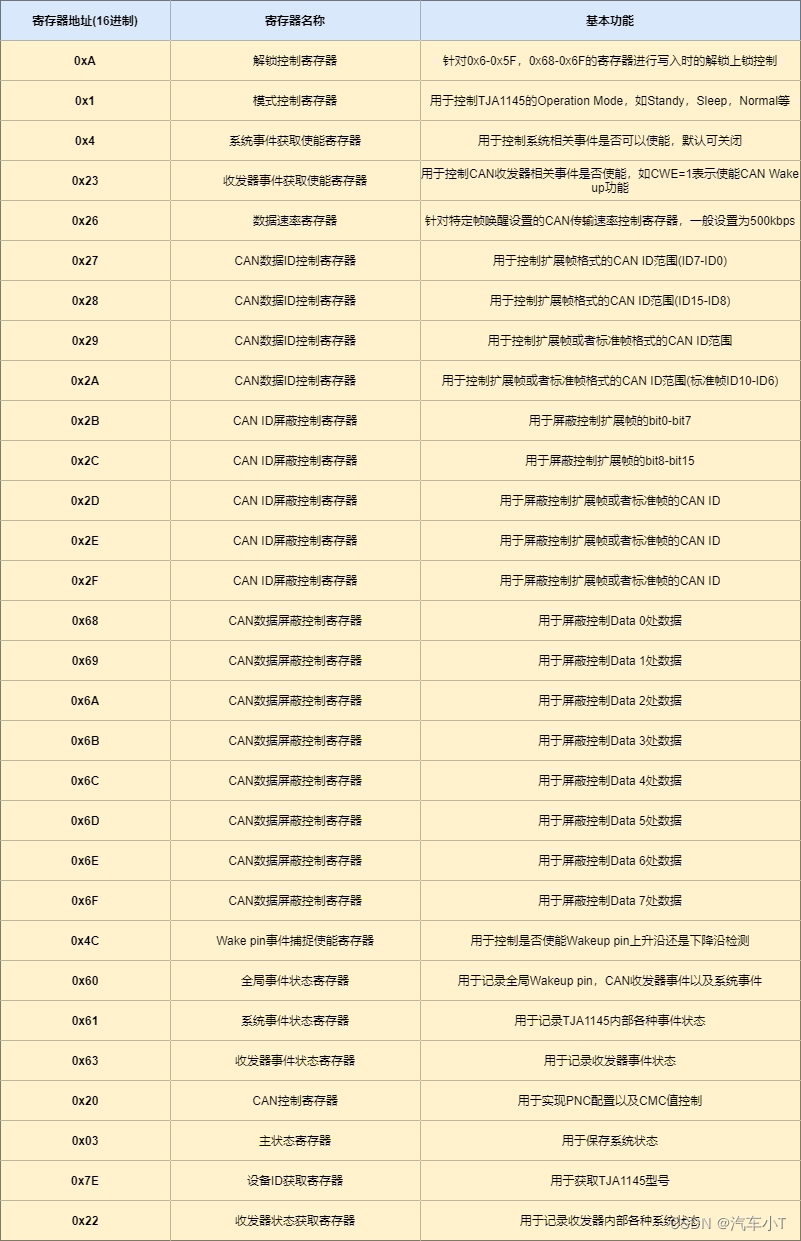
车载ECU休眠唤醒-TJA1145
前言 首先,请教大家几个小小问题,你清楚: 什么是TJA1145吗?你知道休眠唤醒控制基本逻辑是怎么样的吗?TJA1145又是如何控制ECU进行休眠唤醒的呢?使用TJA1145时有哪些注意事项呢? 今天ÿ…...

平衡二叉树的插入,删除以及平衡调整。
一,平衡二叉树插入失衡情况及解决方案 由于各种的插入导致的不平衡,每次调整都是最小不平衡子树。 LL:由于在结点A的 左孩子的左子树 插入结点导致失衡。 右单旋:①将A的 左孩子B 向右上旋转 代替A成为根节点 ②将A结…...

评价指标计算
混淆矩阵: 准确率(Precision):记为P_i,表示被正确预测为类别i的样本数占所有被预测为类别i的样本数的比例。 召回率(Recall):记为R_i,表示被正确预测为类别i的样本数占…...
Spring Boot如何实现OAuth2授权?
Spring Boot如何实现OAuth2授权? OAuth2是一种授权框架,用于授权第三方应用程序访问受保护的资源。在Web应用程序中,OAuth2通常用于授权用户访问受保护的API。 在本文中,我们将介绍如何使用Spring Boot实现OAuth2授权。我们将使…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...
