平衡二叉树的插入,删除以及平衡调整。
一,平衡二叉树插入失衡情况及解决方案
由于各种的插入导致的不平衡,每次调整都是最小不平衡子树。
LL:由于在结点A的 左孩子的左子树 插入结点导致失衡。
右单旋:①将A的 左孩子B 向右上旋转 代替A成为根节点
②将A结点 向右下旋转 成为B的 右子树 的根节点
③B的原来 右子树 成为A的 左子树。
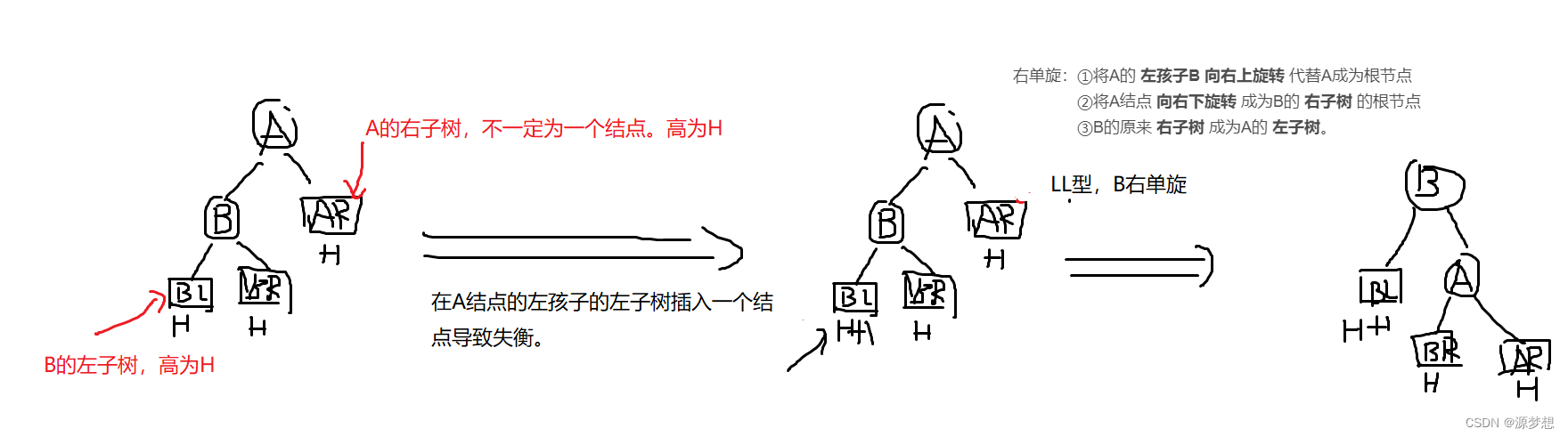
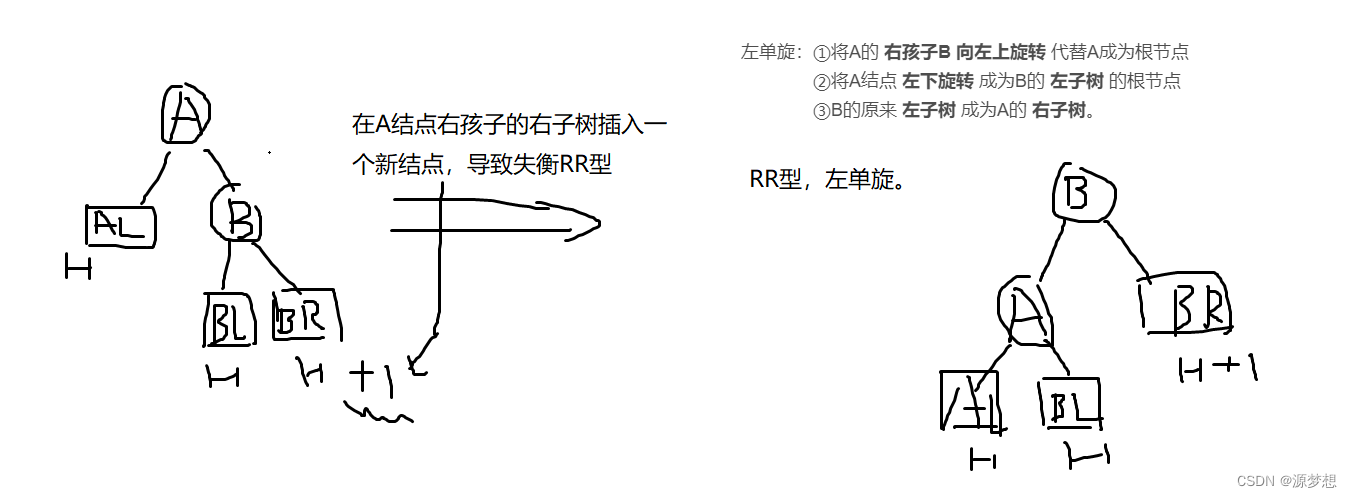
RR:由于在结点A的 右孩子的右子树 插入结点导致失衡。
左单旋:①将A的 右孩子B 向左上旋转 代替A成为根节点
②将A结点 左下旋转 成为B的 左子树 的根节点
③B的原来 左子树 成为A的 右子树。
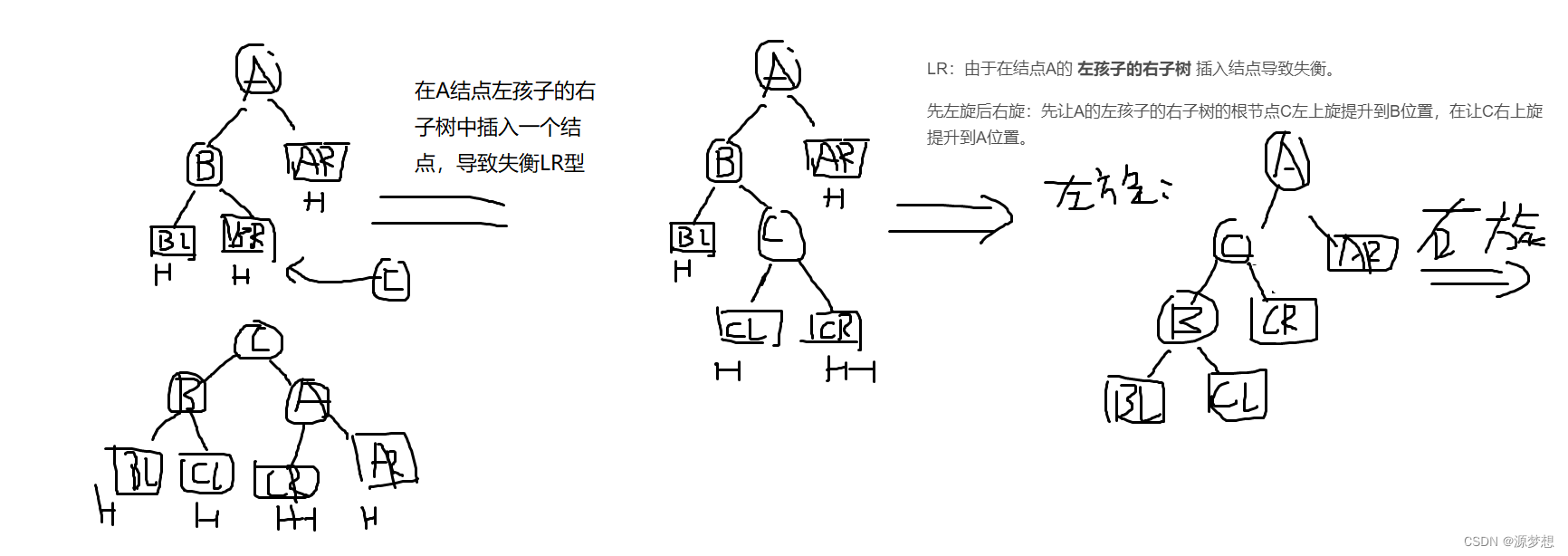
LR:由于在结点A的 左孩子的右子树 插入结点导致失衡。
先左旋后右旋:先让A的左孩子B的右子树的根节点C左上旋提升到B位置,在让C右上旋提升到A位置。
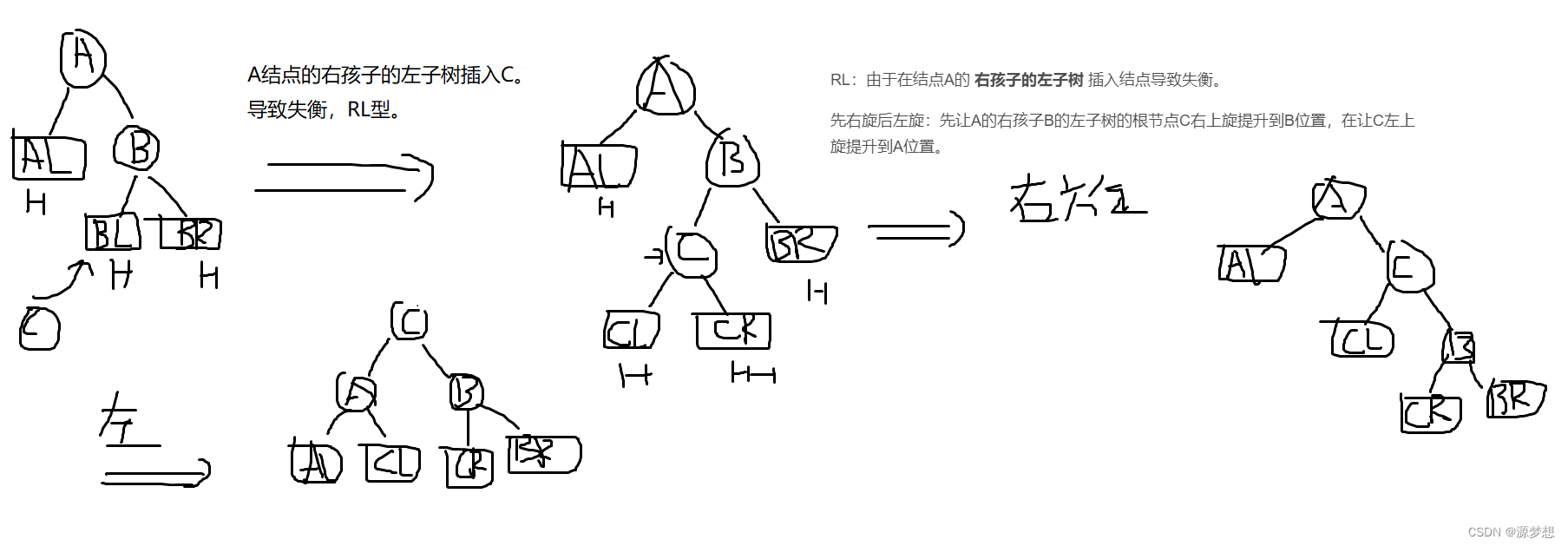
RL:由于在结点A的 右孩子的左子树 插入结点导致失衡。
先右旋后左旋:先让A的右孩子B的左子树的根节点C右上旋提升到B位置,在让C左上旋提升到A位置。
二,平衡二叉树删除步骤
①删除结点(方法同二叉排序树)
1.如果删除的是叶子结点,直接删除。
2.如果删除的结点只有一颗子树,则用子树顶替删除位置。
3.如果删除的结点有两颗子树,则直接前驱(或直接后继)结点顶替,并转为对直接前驱(或直接后继)的删除。
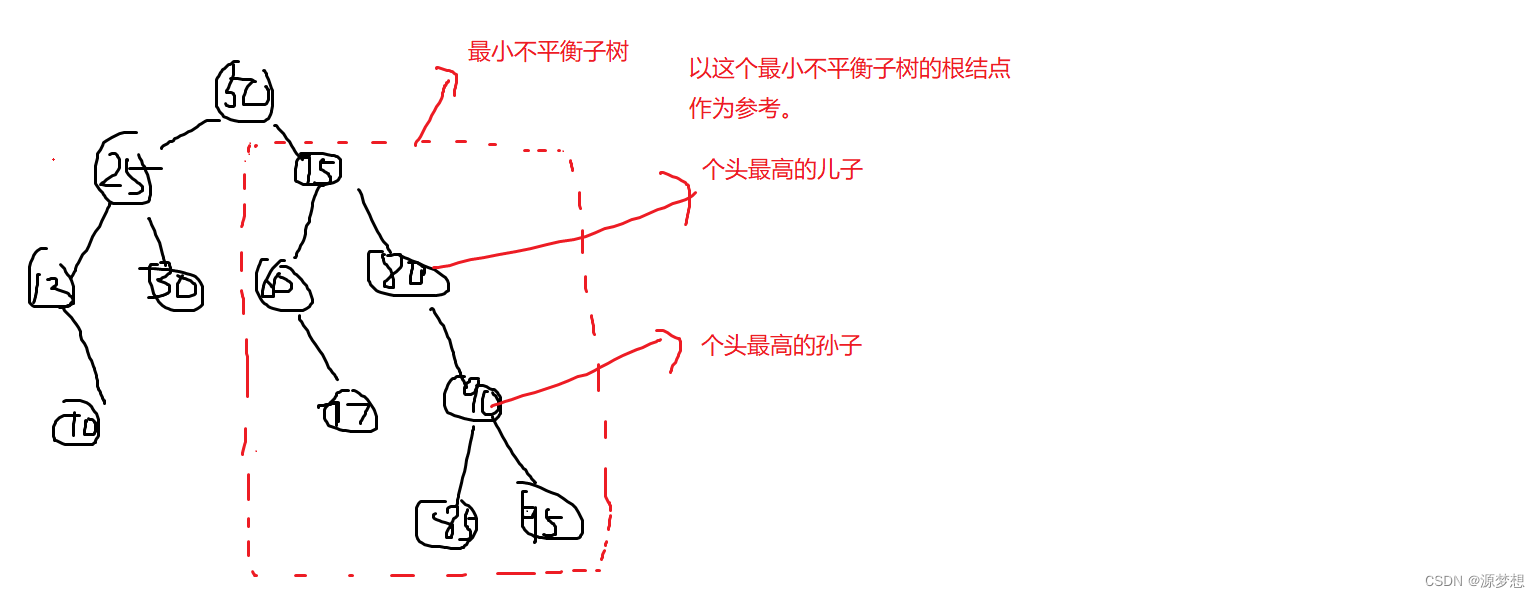
②一路向北(上)找到最小不平衡子树,找不到就结束。
③找到最小不平衡子树下,“个头最大”的儿子和孙子。
④根据孙子位置,调整平衡(孙子相对于爷位置LL,RR,LR,RL)。
1.如果孙子在LL,儿子右单旋。
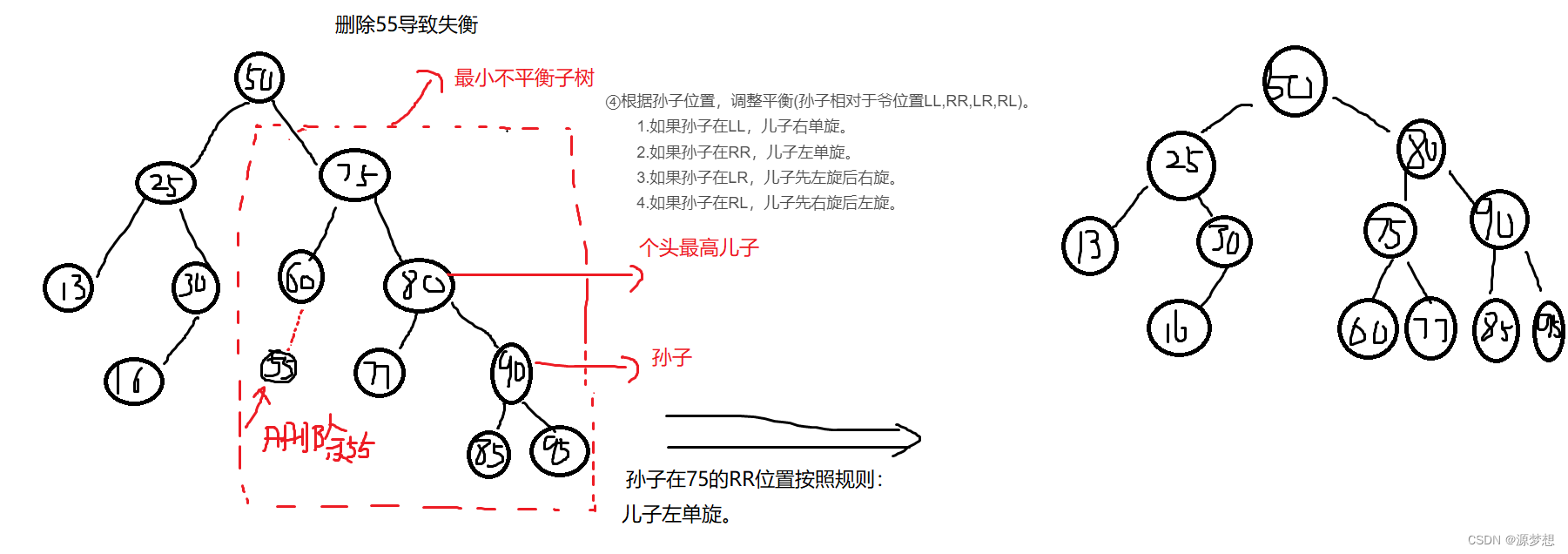
2.如果孙子在RR,儿子左单旋。
3.如果孙子在LR,孙子先左旋后右旋。
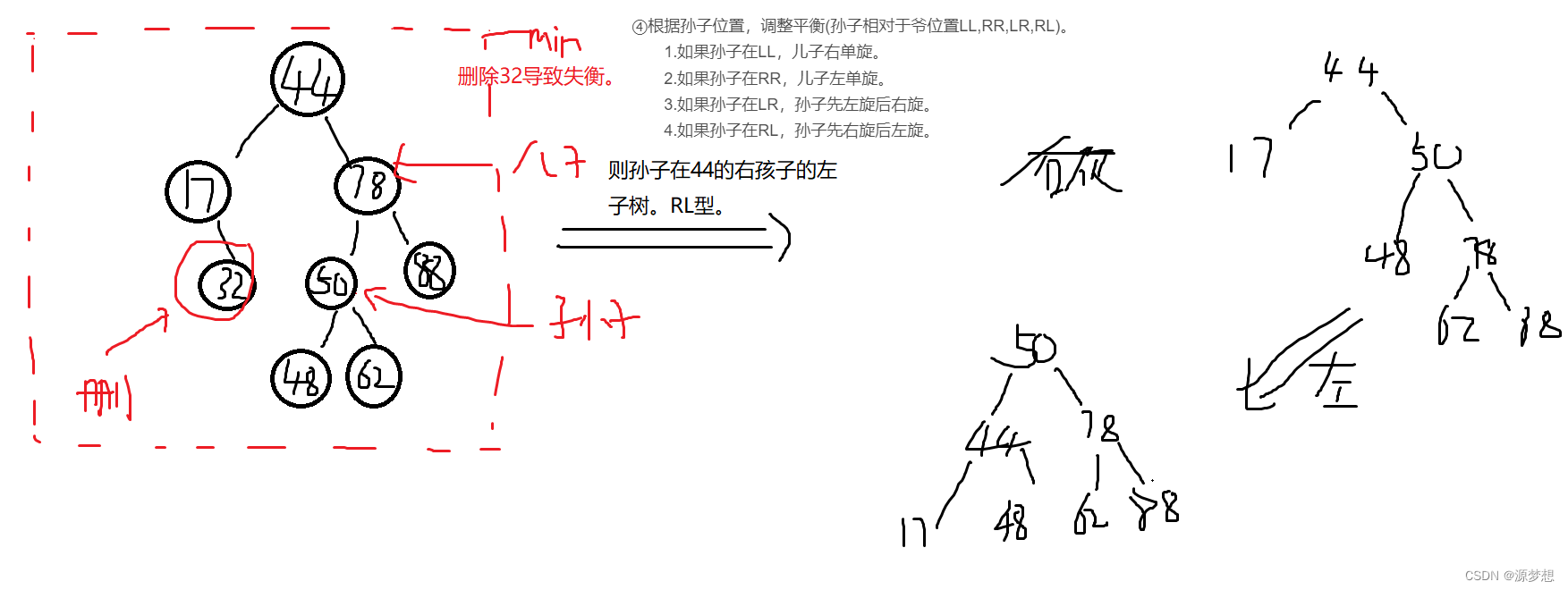
4.如果孙子在RL,孙子先右旋后左旋。
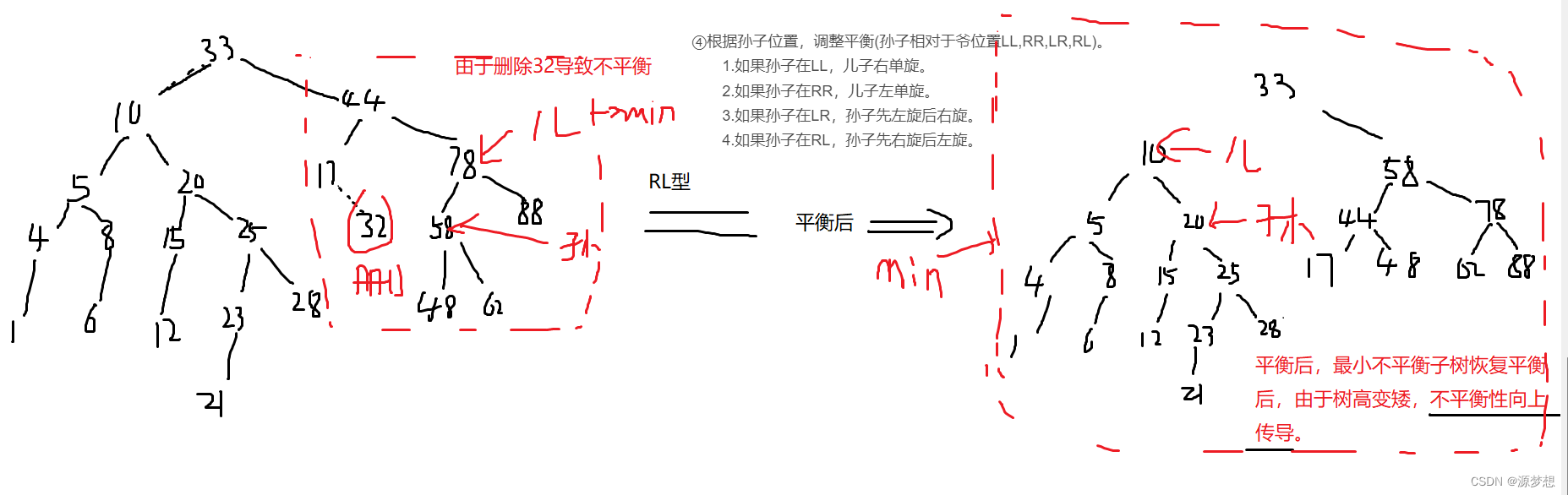
⑤如果不平衡向上传导,继续②。
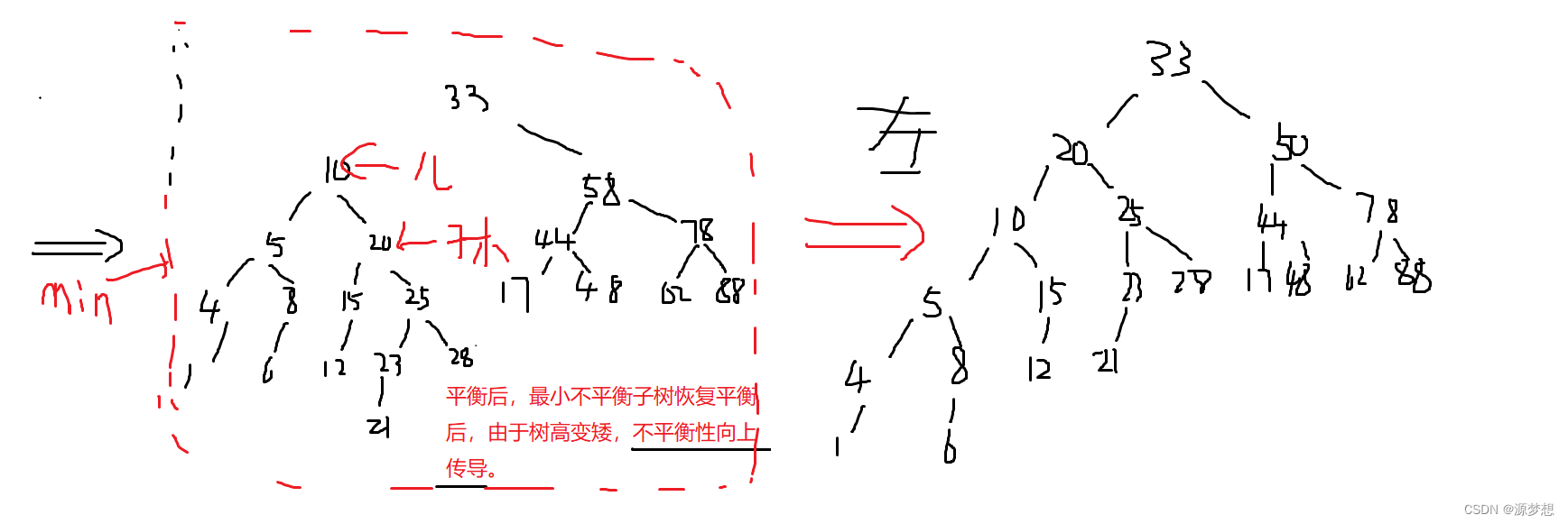
三,平衡二叉树删除实例
1.RR型
1.RL型
1.平衡向上传导

相关文章:

平衡二叉树的插入,删除以及平衡调整。
一,平衡二叉树插入失衡情况及解决方案 由于各种的插入导致的不平衡,每次调整都是最小不平衡子树。 LL:由于在结点A的 左孩子的左子树 插入结点导致失衡。 右单旋:①将A的 左孩子B 向右上旋转 代替A成为根节点 ②将A结…...

评价指标计算
混淆矩阵: 准确率(Precision):记为P_i,表示被正确预测为类别i的样本数占所有被预测为类别i的样本数的比例。 召回率(Recall):记为R_i,表示被正确预测为类别i的样本数占…...
Spring Boot如何实现OAuth2授权?
Spring Boot如何实现OAuth2授权? OAuth2是一种授权框架,用于授权第三方应用程序访问受保护的资源。在Web应用程序中,OAuth2通常用于授权用户访问受保护的API。 在本文中,我们将介绍如何使用Spring Boot实现OAuth2授权。我们将使…...
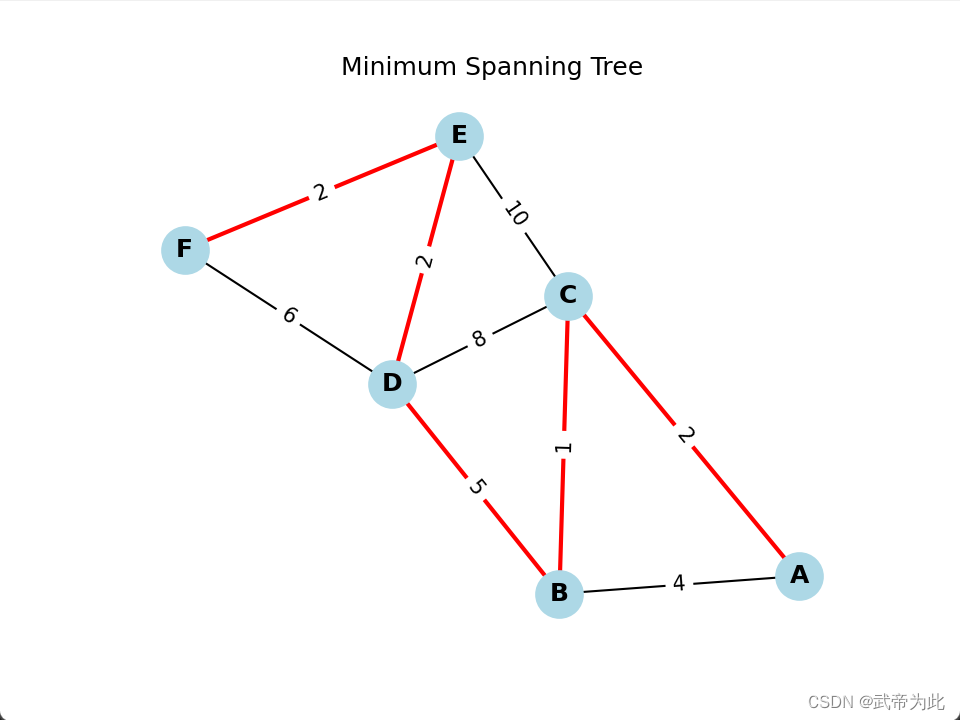
【最小生成树模型】
最小生成树(Minimum Spanning Tree)模型原理与应用 引言 最小生成树(Minimum Spanning Tree,简称MST)是图论中的经典问题之一,它在实际应用中有着广泛的应用。本文将介绍最小生成树模型的原理和应用&…...

【JavaSE】Java基础语法(三十):HashMap与TreeMap
文章目录 1. HashMap1.1 HashMap集合概述和特点1.2 HashMap集合应用案例 2. TreeMap2.1 TreeMap集合概述和特点2.2 TreeMap集合应用案例一2.3 TreeMap集合应用案例二 3. 总结 1. HashMap 1.1 HashMap集合概述和特点 HashMap底层是哈希表结构的依赖hashCode方法和equals方法保…...

Sangria:类似Nova folding scheme的relaxed PLONK for PLONK
1. 引言 前序博客有: Nova: Recursive Zero-Knowledge Arguments from Folding Schemes学习笔记SuperNova:为多指令虚拟机执行提供递归证明基于Nova/SuperNova的zkVMSangria:PLONK Folding2023年 ZK Hack以及ZK Summit 亮点记 主要见2023…...

【蓝桥杯省赛真题22】python剩余空间问题 青少年组蓝桥杯比赛python编程省赛真题解析
目录 python剩余空间问题 一、题目要求 1、编程实现 二、解题思路...

基于深度学习的高精度牙齿健康检测识别系统(PyTorch+Pyside6+YOLOv5模型)
摘要:基于深度学习的高精度牙齿健康检测识别系统可用于日常生活中检测牙齿健康状况,利用深度学习算法可实现图片、视频、摄像头等方式的牙齿目标检测识别,另外支持结果可视化与图片或视频检测结果的导出。本系统采用YOLOv5目标检测模型训练数…...

C++的类
类的性质 上文的例子中用到了类,也知道了类的定义方法,其实类还有更多的性质,这些更多的性质完整支持了面向对象编程。 封装 以前说过,程序就是数据和代码的组合。而C又正好提供了对数据的封装功能,这就可以很好的完…...

【网络】- TCP/IP四层(五层)协议 - 网际层(网络层) - 划分子网、构造超网
目录 一、概述二、分类IP地址不合理的地方三、划分子网四、无分类编址方法 一、概述 前面的文章介绍了网络层的网际协议IP,介绍了IP地址的定义,知道了IP地址分为网络标识(网络地址)、主机标识(主机地址)两部分,也清楚了最初IP地址是按照分类被…...
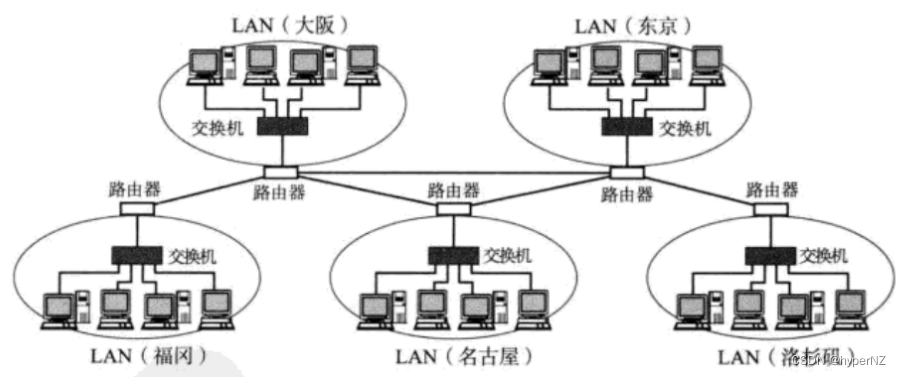
1-网络初识——网络发展史
目录 1.独立模式 2.网络互联 2.1.局域网(Local Area Network,简称LAN) ①基于网线直连 ②基于集线器组建 ③基于交换机组建 ④基于交换机(网口很多)和路由器组建 2.2.广域网(Wide Area Network&…...
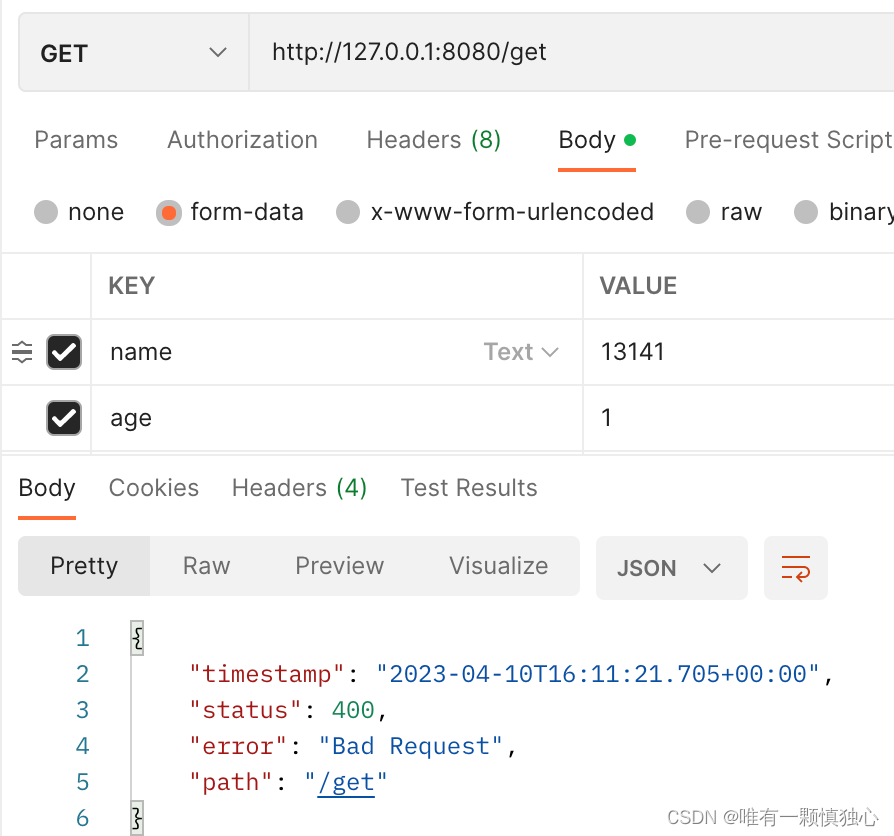
《Spring Guides系列学习》guide35 - guide40
要想全面快速学习Spring的内容,最好的方法肯定是先去Spring官网去查阅文档,在Spring官网中找到了适合新手了解的官网Guides,一共68篇,打算全部过一遍,能尽量全面的了解Spring框架的每个特性和功能。 接着上篇看过的gu…...

《算法导论》拓展之 一维二维最近点对问题
一维点对问题 描述:一维最近点对问题是指在给定的一维点集中找到距离最近的两个点。具体来说,给定一维坐标轴上的 n 个点,要找出其中的两个点,使它们的距离最小。 解决办法:解决这个问题的一种常见方法是使用排序和线…...

【C++】动态存储分配
动态存储分配是指在程序运行时根据需要动态地分配和释放内存空间。 C中提供了两个关键的运算符用于动态存储分配:new和delete。 使用new运算符可以在堆(heap)上动态地分配内存空间,并返回所分配内存的首地址。语法如下࿱…...
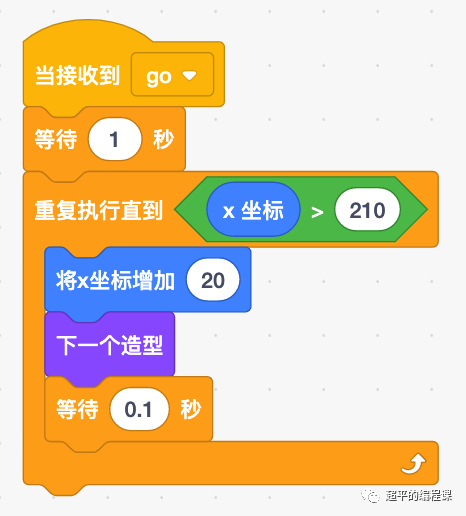
小狗避障-第14届蓝桥杯省赛Scratch中级组真题第4题
[导读]:超平老师的《Scratch蓝桥杯真题解析100讲》已经全部完成,后续会不定期解读蓝桥杯真题,这是Scratch蓝桥杯真题解析第139讲。 小狗避障,本题是2023年5月7日举行的第14届蓝桥杯省赛Scratch图形化编程中级组编程第4题…...
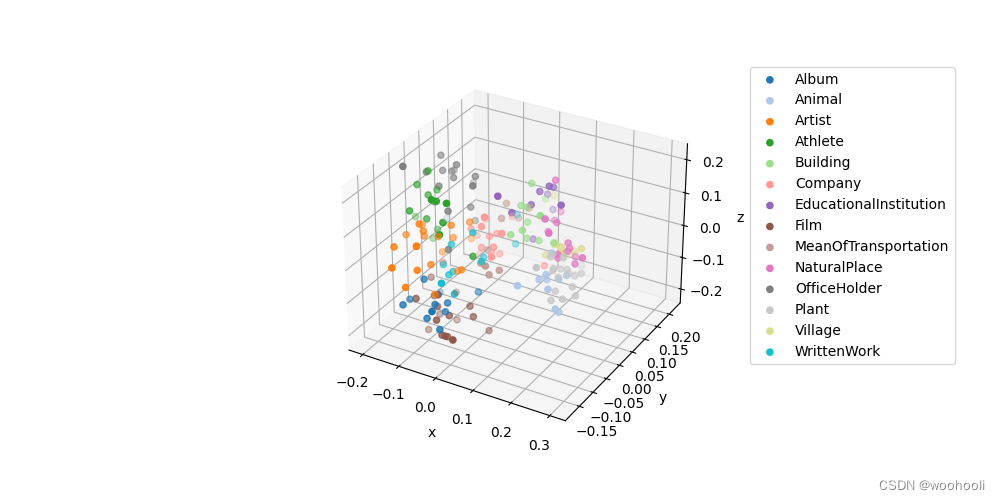
GPT学习笔记-Embedding的降维与2D,3D可视化
嵌入(Embedding)在机器学习和自然语言处理中是一种表示离散变量(如单词、句子或整个文档)的方式,通常是作为高维向量或者矩阵。嵌入的目标是捕捉到输入数据中的语义信息,使得语义相近的元素在嵌入空间中的距…...

Nautilus Chain上线主网,为DeFi和流支付的未来构建基础
近日,加密行业权威平台 Coinmarketcap 发表了一篇名为“Zebec 模块化 Layer3 链 Nautilus Chain上线主网,为 DeFi 和流支付的未来构建基础”的文章,文中对 Zebec 生态公链 Nautilus Chain 的生态进展进行了简要的报道,并对其进行了…...

java设计模式之命令设计模式的前世今生
命令设计模式是什么? 命令设计模式是一种行为型设计模式,它允许将请求封装为对象,并将其传递给调用者,从而使调用者可以在不知道请求具体细节的情况下进行操作。命令模式的主要目的是解耦请求的发送者和接收者,以及通…...
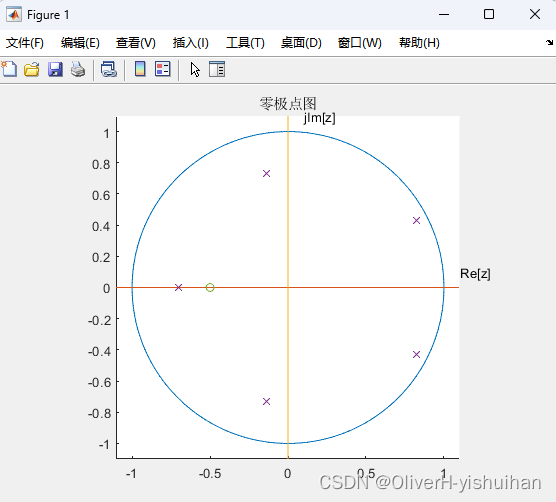
离散系统函数零积点分析
离散系统函数零积点分析 在 Matlab中,系统函数的零极点就可以通过函数 roots 得到。 函数的零极点也可以通过函数 tf2zp 获得,其调用格式为:[Z, P, K] tf2zp(B, A),函数 tf2zp 可以将H(z)的有理分式转换为零极点增益形式&#…...

Karl Guttag:苹果VST MR头显也无法突破AR的物理局限
据近期的爆料、传闻显示,苹果将6月份的WWDC2023上首次公布AR/VR头显。对此,AR/VR光学专家Karl Guttag持怀疑态度,他此前在DisplayDaily的文章中写道,苹果研发AR/VR头显更像是担心错过新技术趋势。回顾过去的一些关键的AR产品&…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
