【最小生成树模型】
最小生成树(Minimum Spanning Tree)模型原理与应用
引言
最小生成树(Minimum Spanning Tree,简称MST)是图论中的经典问题之一,它在实际应用中有着广泛的应用。本文将介绍最小生成树模型的原理和应用,并通过一个实战项目来演示如何使用Python实现最小生成树算法。
最小生成树模型原理
最小生成树是一个连通无向图的生成树,它包含了图中所有的顶点,但只有足够的边来使得树连通且权重之和最小。最小生成树模型有以下两个基本性质:
- 最小生成树是一个树,即无环连通图。
- 最小生成树的权重之和最小。
最常用的求解最小生成树的算法是Prim算法和Kruskal算法。
Prim算法
Prim算法从一个起始顶点开始,逐步扩展最小生成树,直到包含所有顶点。算法的基本步骤如下:
- 选择一个起始顶点作为树的根节点,将其加入最小生成树。
- 从与最小生成树相邻的顶点中选择一个最短边连接到树上,将该顶点加入最小生成树。
- 重复步骤2,直到所有的顶点都被包含在最小生成树中。
Kruskal算法
Kruskal算法通过不断添加权重最小的边来构建最小生成树,直到所有顶点都被包含在树中。算法的基本步骤如下:
- 将图中的边按照权重从小到大进行排序。
- 依次从排序后的边中选择权重最小的边,若该边的两个顶点不在同一连通分量中,则将该边加入最小生成树,并将两个顶点合并到同一连通分量中。
- 重复步骤2,直到所有的顶点都被包含在最小生成树中。
最小生成树模型应用
最小生成树模型在实际应用中有着广泛的应用,以下是一些常见的应用场景:
网络设计
在计算机网络设计中,最小生成树模型可以用来构建网络拓扑结构,以便实现最优的网络连接。
物流和运输
在物流和运输领域,最小生成树模型可以用来确定最优的运输路线,以减少成本和提高效率。
电力传输
在电力传输网络中,最小生成树模型可以帮
助确定最优的输电线路,以减少能源损失和提高能源利用率。
集群分析
在数据分析和机器学习中,最小生成树模型可以用来进行集群分析,帮助发现数据集中的特定模式和关联性。
实战项目:最小生成树的应用
下面我们将通过一个例子来演示如何使用Python实现最小生成树算法。假设我们有一个城市的地图,我们需要找到连接所有城市的最优道路网络。
步骤
步骤1:准备数据
首先,我们需要准备城市地图的数据。数据可以包括城市之间的距离或权重,以及城市的坐标信息。在这个示例中,我们将使用一个包含5个城市的简单地图。
步骤2:构建图结构
使用Python中的图结构表示城市地图,并添加城市之间的边和权重。
import networkx as nx# 创建图对象
G = nx.Graph()# 添加城市之间的边和权重
G.add_edge('A', 'B', weight=4)
G.add_edge('A', 'C', weight=2)
G.add_edge('B', 'C', weight=1)
G.add_edge('B', 'D', weight=5)
G.add_edge('C', 'D', weight=8)
G.add_edge('C', 'E', weight=10)
G.add_edge('D', 'E', weight=2)
G.add_edge('D', 'F', weight=6)
G.add_edge('E', 'F', weight=2)
步骤3:求解最小生成树
使用Prim算法或Kruskal算法求解最小生成树,并获取最小生成树的边列表。
from networkx.algorithms import minimum_spanning_tree# 使用Prim算法求解最小生成树
mst = minimum_spanning_tree(G, algorithm='prim')# 获取最小生成树的边列表
edges = list(mst.edges(data=True))
步骤4:可视化结果
使用matplotlib和networkx库将最小生成树可视化。
# 创建画布和子图对象
import matplotlib.pyplot as pltfig, ax = plt.subplots()# 绘制城市地图
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, node_size=500, node_color='lightblue', font_size=12, font_weight='bold', ax=ax)# 绘制最小生成树的边
nx.draw_networkx_edges(G, pos, edgelist=edges, width=2, edge_color='red', ax=ax)# 添加每条边的权重和初始节点
edge_labels = nx.get_edge_attributes(G, 'weight')
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, font_size=10)plt.title('Minimum Spanning Tree')
plt.axis('off')
plt.show()
结果如图:
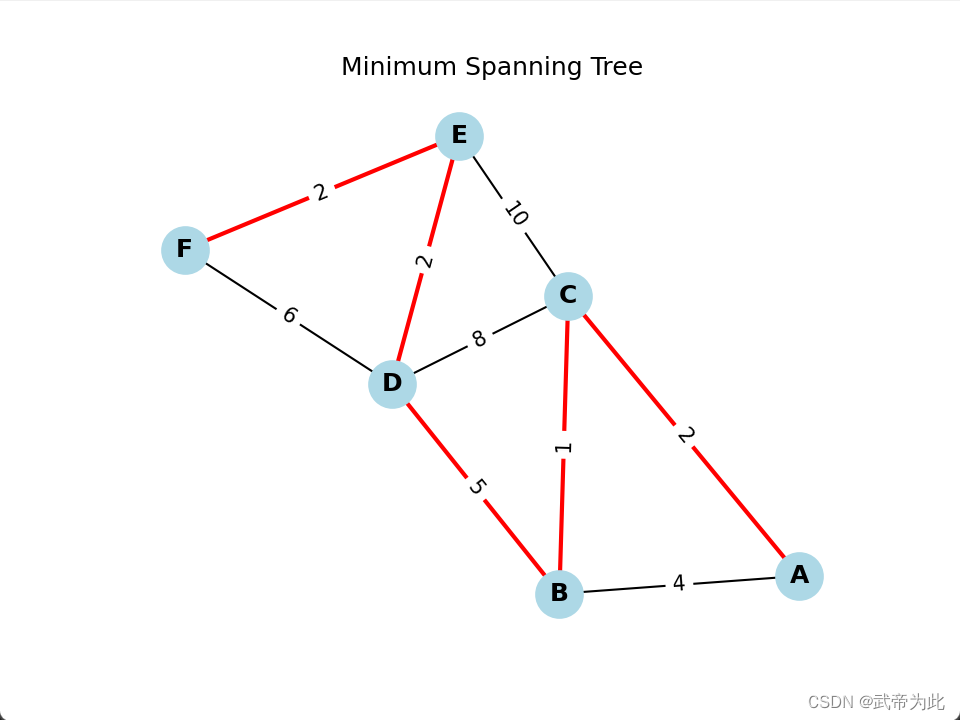
结论
最小生成树模型在实际应用中有着广泛的应用。通过掌握最小生成树模型,我们可以在各种领域中找到最优的连接方式,以减少成本和提高效率。
相关文章:

【最小生成树模型】
最小生成树(Minimum Spanning Tree)模型原理与应用 引言 最小生成树(Minimum Spanning Tree,简称MST)是图论中的经典问题之一,它在实际应用中有着广泛的应用。本文将介绍最小生成树模型的原理和应用&…...

【JavaSE】Java基础语法(三十):HashMap与TreeMap
文章目录 1. HashMap1.1 HashMap集合概述和特点1.2 HashMap集合应用案例 2. TreeMap2.1 TreeMap集合概述和特点2.2 TreeMap集合应用案例一2.3 TreeMap集合应用案例二 3. 总结 1. HashMap 1.1 HashMap集合概述和特点 HashMap底层是哈希表结构的依赖hashCode方法和equals方法保…...

Sangria:类似Nova folding scheme的relaxed PLONK for PLONK
1. 引言 前序博客有: Nova: Recursive Zero-Knowledge Arguments from Folding Schemes学习笔记SuperNova:为多指令虚拟机执行提供递归证明基于Nova/SuperNova的zkVMSangria:PLONK Folding2023年 ZK Hack以及ZK Summit 亮点记 主要见2023…...

【蓝桥杯省赛真题22】python剩余空间问题 青少年组蓝桥杯比赛python编程省赛真题解析
目录 python剩余空间问题 一、题目要求 1、编程实现 二、解题思路...

基于深度学习的高精度牙齿健康检测识别系统(PyTorch+Pyside6+YOLOv5模型)
摘要:基于深度学习的高精度牙齿健康检测识别系统可用于日常生活中检测牙齿健康状况,利用深度学习算法可实现图片、视频、摄像头等方式的牙齿目标检测识别,另外支持结果可视化与图片或视频检测结果的导出。本系统采用YOLOv5目标检测模型训练数…...

C++的类
类的性质 上文的例子中用到了类,也知道了类的定义方法,其实类还有更多的性质,这些更多的性质完整支持了面向对象编程。 封装 以前说过,程序就是数据和代码的组合。而C又正好提供了对数据的封装功能,这就可以很好的完…...

【网络】- TCP/IP四层(五层)协议 - 网际层(网络层) - 划分子网、构造超网
目录 一、概述二、分类IP地址不合理的地方三、划分子网四、无分类编址方法 一、概述 前面的文章介绍了网络层的网际协议IP,介绍了IP地址的定义,知道了IP地址分为网络标识(网络地址)、主机标识(主机地址)两部分,也清楚了最初IP地址是按照分类被…...
1-网络初识——网络发展史
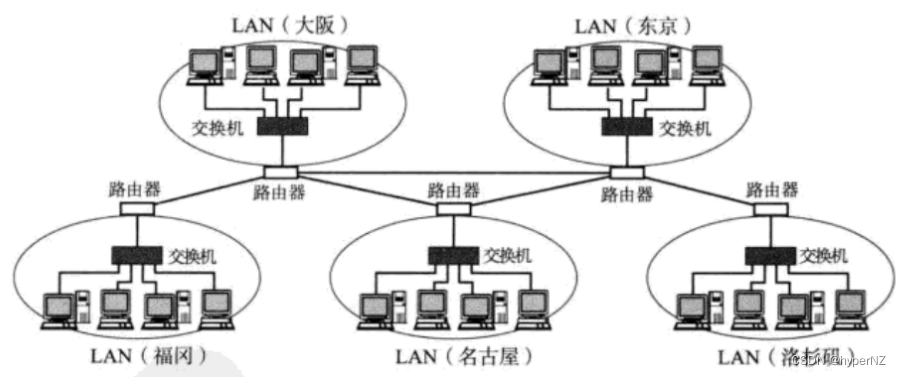
目录 1.独立模式 2.网络互联 2.1.局域网(Local Area Network,简称LAN) ①基于网线直连 ②基于集线器组建 ③基于交换机组建 ④基于交换机(网口很多)和路由器组建 2.2.广域网(Wide Area Network&…...
《Spring Guides系列学习》guide35 - guide40
要想全面快速学习Spring的内容,最好的方法肯定是先去Spring官网去查阅文档,在Spring官网中找到了适合新手了解的官网Guides,一共68篇,打算全部过一遍,能尽量全面的了解Spring框架的每个特性和功能。 接着上篇看过的gu…...

《算法导论》拓展之 一维二维最近点对问题
一维点对问题 描述:一维最近点对问题是指在给定的一维点集中找到距离最近的两个点。具体来说,给定一维坐标轴上的 n 个点,要找出其中的两个点,使它们的距离最小。 解决办法:解决这个问题的一种常见方法是使用排序和线…...

【C++】动态存储分配
动态存储分配是指在程序运行时根据需要动态地分配和释放内存空间。 C中提供了两个关键的运算符用于动态存储分配:new和delete。 使用new运算符可以在堆(heap)上动态地分配内存空间,并返回所分配内存的首地址。语法如下࿱…...
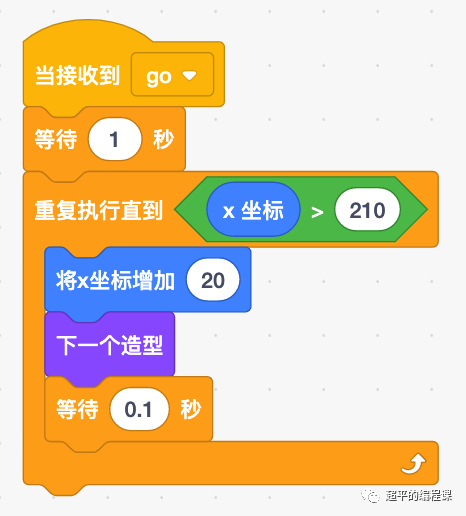
小狗避障-第14届蓝桥杯省赛Scratch中级组真题第4题
[导读]:超平老师的《Scratch蓝桥杯真题解析100讲》已经全部完成,后续会不定期解读蓝桥杯真题,这是Scratch蓝桥杯真题解析第139讲。 小狗避障,本题是2023年5月7日举行的第14届蓝桥杯省赛Scratch图形化编程中级组编程第4题…...
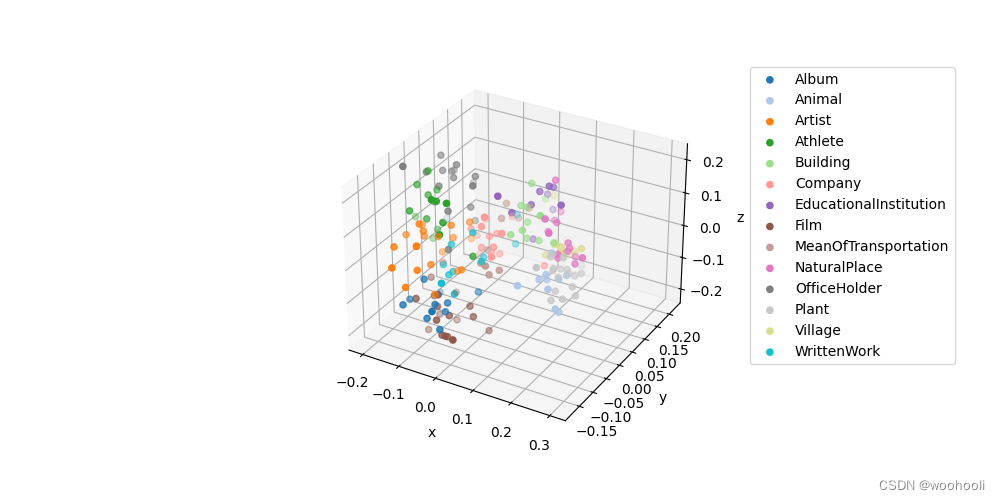
GPT学习笔记-Embedding的降维与2D,3D可视化
嵌入(Embedding)在机器学习和自然语言处理中是一种表示离散变量(如单词、句子或整个文档)的方式,通常是作为高维向量或者矩阵。嵌入的目标是捕捉到输入数据中的语义信息,使得语义相近的元素在嵌入空间中的距…...

Nautilus Chain上线主网,为DeFi和流支付的未来构建基础
近日,加密行业权威平台 Coinmarketcap 发表了一篇名为“Zebec 模块化 Layer3 链 Nautilus Chain上线主网,为 DeFi 和流支付的未来构建基础”的文章,文中对 Zebec 生态公链 Nautilus Chain 的生态进展进行了简要的报道,并对其进行了…...

java设计模式之命令设计模式的前世今生
命令设计模式是什么? 命令设计模式是一种行为型设计模式,它允许将请求封装为对象,并将其传递给调用者,从而使调用者可以在不知道请求具体细节的情况下进行操作。命令模式的主要目的是解耦请求的发送者和接收者,以及通…...
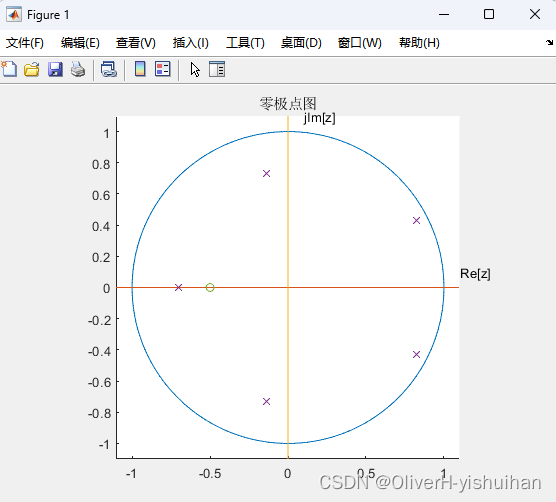
离散系统函数零积点分析
离散系统函数零积点分析 在 Matlab中,系统函数的零极点就可以通过函数 roots 得到。 函数的零极点也可以通过函数 tf2zp 获得,其调用格式为:[Z, P, K] tf2zp(B, A),函数 tf2zp 可以将H(z)的有理分式转换为零极点增益形式&#…...

Karl Guttag:苹果VST MR头显也无法突破AR的物理局限
据近期的爆料、传闻显示,苹果将6月份的WWDC2023上首次公布AR/VR头显。对此,AR/VR光学专家Karl Guttag持怀疑态度,他此前在DisplayDaily的文章中写道,苹果研发AR/VR头显更像是担心错过新技术趋势。回顾过去的一些关键的AR产品&…...
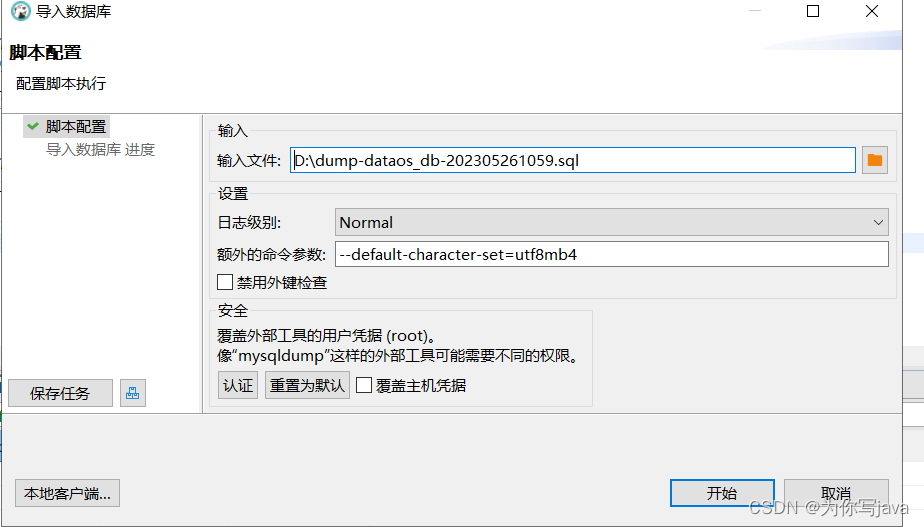
mysql倒库操作遇到的问题
背景:本地windows 10安装了mysql数据库后,需要把远程库的表结构和数据全部导入进来。 操作:导出数据库,导入数据库。 第一步:导出数据库 使用dump命令即可。 登陆mysql数据库 mysql -hhost --default-character-s…...
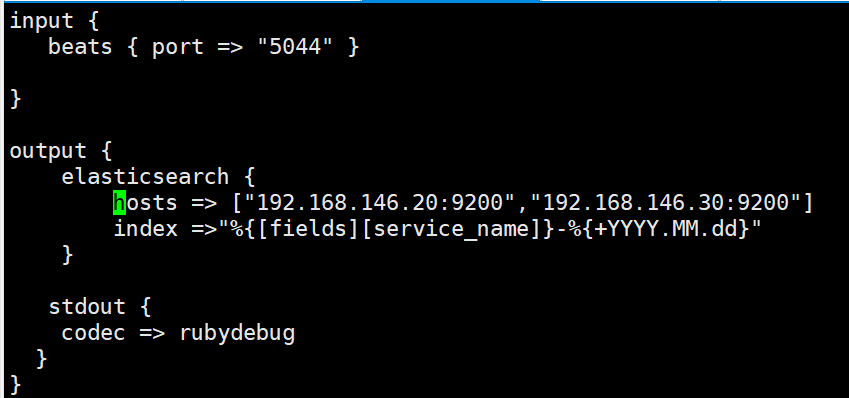
ELK企业级日志分析系统
ELK概述 为什么要使用 ELK 日志主要包括系统日志、应用程序日志和安全日志。系统运维和开发人员可以通过日志了解服务器软硬件信息、检查配置过程中的错误及错误发生的原因。经常分析日志可以了解服务器的负荷,性能安全性,从而及时采取措施纠正错误。 …...

华为OD机试真题 Java 实现【基站维修工程师】【2023Q1 200分】,附详细解题思路
一、题目描述 小王是一名基站维护工程师,负责某区域的基站维护。 某地方有n个基站(1<n<10),已知各基站之间的距离s(0<s<500),并且基站x到基站y的距离,与基站y到基站x的距离并不一定会相同。 小王从基站1出发,途径每个基站1次,然后返回基站1,需要请你…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
